Модель бережливого управления инновационными проектами на основе учета рисков и численной оценки экономической целесообразности выполнения этапов работ

Инновационные проекты отличаются от классических подобно тому, как отличается от классической квантовая физика.

1. Введение

Ключевой задачей определено технологическое развитие страны на основе высоких технологий [1]. Результативность реализации инноваций, согласно статистическим данным, пока невысока. Так, в IT-сфере результативность по отношению к первоначальным идеям не превышает нескольких процентов [2, 3, 5] (Sartori, Ilyina, Mantsevich, 2019; Sartori, Gareev, Ilyina, Mantsevich, 2020), а вероятность коммерциализации для hardware-стартапов еще на порядок ниже. Статистика бизнес-ангелов также подтверждает наличие серьезной проблемы обоснованности выбора проектов для инвестиций. Как показано в [4], только 14% инвестиций определили основную часть дохода.

Существуют как классические, так и современные методы управления проектами (PMBoK [9], Agile, Scrum, Kanban, Six Sigma, PRINCE2 и др. [19]), их активно внедряют акселераторы, техноброкеры, технопарки и другие инновационные структуры. Однако при практической реализации результат их применения не дает должного эффекта, что подтверждается приведенной выше статистикой.

По нашему мнению, отсутствие единой для всех участников инновационного процесса методики количественной оценки готовности инновационных проектов (ИП) на разных стадиях и связанных с ней рисков является ключевой причиной низкой результативности, а следовательно, и низкой рентабельности инвестиций при традиционном подходе к управлению проектами.

В статье на основе авторской гипотезы о статистическом характере распределения инновационных рисков и стоимости проекта по этапам впервые дается ответ на вопрос о численной оценке вероятности успешной коммерциализации проектов.

На этой основе предложена модель гарантированного безубыточного управления портфелем проектов на основе планирования по уровням готовности, оценке экономической целесообразности, регулярному отбору проектов с наименьшим риском. Показано, что в рамках предложенной модели результат инвариантен к форме зависимости рисков от уровней готовности проектов.

2. Инновации – это всегда риск

Новое – это всегда риск.

Кто отвергает риск, тот отвергает новое.

Даниил Гранин, «Иду на грозу»

Уточним понятие риска для целей данной статьи. Большинство работ по теме рисков посвящено качественному описанию групп рисков, их классификации [6–8], что не приближает нас к их численной оценке.

В контексте данной статьи определим риск как вероятность неудачи инновационного проекта. Обратную риску величину назовем вероятностью успеха. За успех примем результат с положительным доходом с учетом всех затрат, включая разработку, а также на проекты портфеля, не завершившиеся успешно.

Основное отличие управления ИП от классических (например, по методике PMBoK [9]) заключается в том, что инновации по своей природе неразрывно связаны с неопределенностями и специфическими рисками: технологическим, производственным, рыночным и другими [2, 10, 11] (Sartori, Ilyina, Mantsevich, 2019; Sartori, Sushkov, Mantsevich, 2020; Sartori, Gareev, Ilyina, Mantsevich, 2020). Помимо этого, жизненный цикл продукта может длиться значительное время, а внешняя среда изменяется быстро и часто непредсказуемо. С ней могут меняться облик продукта, сектора рынка, корректироваться начальные цели и экономика проекта.

Риски являются движущей силой ИП. Именно новизна является основой создания критических преимуществ инновационного продукта. Научное исследование, в отличие от производственного процесса, делается один раз, и нет возможности количественно определить его риски, повторяя исследование для набора статистики.

Результат инновационного проекта складывается из большого числа случайных не зависящих друг от друга внутренних и внешних факторов. Неудачные инновационные проекты не всегда являются следствием ошибок менеджмента. Это проявление общей закономерности процесса создания нового, реализации инновационных рисков. По этой причине управление случайными факторами, рисками в ИП важно построить на научных принципах.

В данной статье на основе численных выражений для разных групп рисков предложена методика экспресс-оценки экономической целесообразности ИП для разных уровней их готовности. В методике применена параметрическая модель на базе вероятностных методов и гипотез, сформулированных с учетом статистических данных по выполненным проектам. Параметры модели впоследствии могут быть проверены и откорректированы на практике конкретных портфелей инновационных проектов. Основа методики – учет рисков достижения условий, содержащихся в параметрах инновационной готовности (ПИНГ) для различных значений уровней готовности [2] (Sartori, Ilyina, Mantsevich, 2019).

Подчеркнем, что идеальное решение по расчету численных значений рисков в данном случае невозможно и не является нашей целью. Нас интересует практическое решение, поэтому математические абстракции будут упрощены до приемлемого на практике уровня достоверности.

Методология ПИНГ [2] (Sartori, Ilyina, Mantsevich, 2019) содержит перечень основных типов рисков, присущих ИП, исследованиям и разработкам. Она включает шесть основных условно независимых аспектов инновационного проекта и групп рисков соответственно. К ним относятся технологическая (TRL), производственная (MRL), интеграционная (IRL), организационная (ORL) готовность, преимущества и риски (BRL), а также рыночная готовность (CRL). Для ПИНГ разработаны шкалы оценки проекта по уровням готовности продукта разработки в едином цифровом формате, понятном всем заинтересованным в успешной реализации проекта сторонам.

В инвестиционных проектах, не относящихся к инновационным, также ведется учет рисков. Он сводится часто к оценке основных показателей инвестиционного проекта (NPV, ROI и др.) [12]. Однако не стоит заблуждаться и считать эти показатели абсолютно точными критериями. Неопределенности возникают из-за сложности в корректном определении основных исходных параметров, таких как цена продукта, объем продаж по годам, себестоимость, рентабельность. В рамках настоящей работы мы ограничимся исключительно инновационными рисками, связанными с ПИНГ. При этом показатели NPV, ROI и другие подобные можно использовать для дополнительной характеризации проекта на высоких уровнях развития.

Инновационные продукты отличаются тем, что они не являются стандартными. Возможно ли рассчитать точно перечисленные экономические параметры на ранних уровнях готовности нового для рынка продукта, у которого часто не ясны окончательно его облик, ценностное предложение, облик потребителя, доля рынка, рыночная цена и себестоимость производства и продаж?

Доля рынка зависит от ценностного предложения, а оно зависит, в свою очередь, от цены и качества; на цену влияет себестоимость, которая определяется производством, а производственные технологии ограничены целевым значением себестоимости, определяемой рынком; отсюда происходит корректировка технологии и ценностного предложения. Круг замыкается. Приходится инвест-менеджерам делать прогнозы и допущения, не подкрепленные реальными основаниями. Следовательно, достоверность таких решений часто невелика.

Но самый важный недостаток принятия решения об инвестировании на основе NPV-проекта – это отсутствие учета вероятности достижения успешного результата каждого этапа проекта, реализации инновационных рисков.

При тщательном рассмотрении составляющих успеха ИП становится понятно, что финансовые риски гораздо шире рамок, ограниченных параметрами NPV, ROI и их аналогами. Риски присутствуют во всех шести ПИНГ на каждом их уровне. Они влияют на вероятность достижения положительного коммерческого результата и должны быть учтены.

Как цена проектов в инновационном портфеле, так и цена их отдельных этапов является первостепенным фактором риска. Цена формируется исполнителем проекта без должной детализации затрат, с запасом надежности, что весьма часто приводит к неоправданно завышенным значениям, таким, что ожидаемый экономический эффект от внедрения результата продукта может не окупить понесенных затрат.

В решении задачи адекватного учета и количественной оценки финансовых рисков инновационного проекта на разных этапах его реализации мы видим ключ к повышению доли коммерциализуемых результатов, решению проблемы повышения степени доверия к планируемым результатам и привлечения инвестиций.

3. Постановка задачи увеличения эффективности инвестиций в инновационные проекты

Риск – пятый туз в любой колоде.

Борис Васильев, «Утоли моя печали»

Уточним практическое понимание смысла численных значений инновационных рисков. Что означает, что у проекта есть риски, приводящие к вероятности его успешной реализации, например 1/10? Это означает, что в среднем из десяти проектов с такой величиной риска успешно реализуется только один проект портфеля. Какова судьба остальных девяти проектов? Они не состоятся, и все понесенные затраты на эти проекты нужно компенсировать из прибыли других проектов портфеля, что, естественно, снижает его суммарную доходность.

Мы ставим задачу получения положительной рентабельности и увеличения эффективности инвестиций в ИП. Способ решения понятен: нужно обеспечить постоянный отсев высокорисковых проектов на основе ранней диагностики их реализации и выявление конкретных устраняемых рисков остающихся в портфеле проектов для их компенсации.

Уменьшение числа проектов в портфеле иллюстрирует рисунок 1. Из него следует, что в данном примере до девятого уровня готовности успешно доходит только пять проектов. При этом на третьем уровне готовности число проектов в 20 раз больше. Следовательно, 95 проектов было отсеяно, остановлено, отнесено к категории научных исследований.

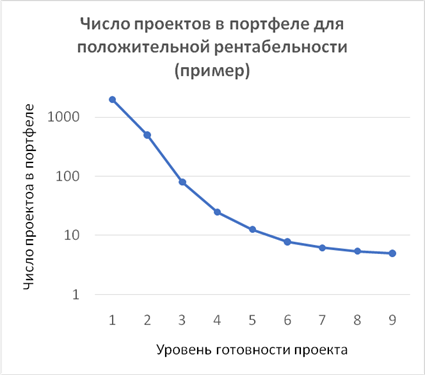
Рисунок 1. Пример изменения числа проектов в портфеле: число проектов уменьшается при реализации рисков с ростом уровня готовности (Обсуждение данной зависимости приводится в разделе 9)

Источник: составлено авторами.

Для выбора наиболее перспективных проектов и, соответственно, для отсева проектов с высоким риском нужны объективные критерии. Приступим к их формулировке.

4. Критерий учета величины допустимых финансовых рисков проекта

Не доказано, что риск – дело благородное, но благородное дело – это почти всегда риск.

Вольтер

Мы упоминали ранее о присутствии значительной неопределенности в расчете NPV (IRR, ROI) по традиционным формулам применительно к ИП. Вместе с тем этот инструмент хорошо освоен и широко применяется в проектном менеджменте. Поэтому нашей задачей является использование NPV для расчета финансовых рисков инновационных проектов и их этапов при условии введения корректирующих поправок на инновационные риски. Поправок весьма значимых, как мы увидим далее.

ИП неповторимы, невозможно набрать статистику успешности выполнения проекта, повторяя его вновь и вновь. Поэтому воспользуемся переходом от усреднения по времени к усреднению по ансамблю – портфелю проектов [1]. Заранее отметим ограничение: предлагаемый подход, как любой статистический подход, дает математически точный результат при стремлении числа проектов к бесконечности. Однако для практических целей на ограниченном числе проектов он дает разумное и достаточное приближение, показывая тенденции, следование которым в итоге приведет к положительному финансовому результату.

Оценим ожидаемую прибыль V от реализации портфеля из M инновационных проектов, каждый из которых реализуется с ожидаемым чистым дисконтированным доходом NPV_i и вероятностью p_i как математическое ожидание суммы случайных величин для единичных проектов:

≈ V [2]. (1)

В силу отмеченных в разделе 2 особенностей NPV не учитывает затраты С на разработку продуктов в рамках ИП. Таким образом, портфель окажется эффективным, и рентабельность его будет положительной при условии, что сумма затрат на весь портфель проектов C окажется меньше суммарного NPV. Отсюда выводим следующий очевидный критерий положительной рентабельности портфеля проектов:

V > C. (2)

В силу самостоятельности и независимости каждого проекта и отличной от нуля вероятности остановки любого проекта из портфеля при реализации неблагоприятных рисков, в целях минимизации рисков портфеля для каждого проекта должно соблюдаться неравенство, аналогичное выражению (2), а именно:

, (3)

где C_i – суммарная цена всех стадий разработки и выведения на рынок продукта проекта i;

NPVi – чистый дисконтированный доход проекта i без учета затрат на разработку.

Подчеркнем, что в силу существенной неопределенности в величине стоимости разработки продукта мы не включаем ее в расчет затрат в NPV, вынося в правую часть неравенств (2) и (3).

Аналогично выражению (2) неравенство (3) формулирует условие: если цена проекта C_i меньше математического ожидания NPV проекта, то проект экономически целесообразен. И наоборот, если затраты превышают математическое ожидание NPV проекта, то проект будет затратным.

Выражение (3) принципиально отличается от традиционного инвестиционного критерия наличием множителя pi в левой части и цены Сi в правой части. Множитель pi, значение которого обсудим и определим в разделе 6 (S- и Q-кривые для уровней готовности проекта), отражает вероятностный характер управления инновационным портфелем и показывает, насколько прибыль от удачного проекта должна превосходить затраты на его разработку, чтобы дополнительно компенсировать средства, потраченные на неудачные проекты.

5. Экспресс-оценка экономической целесообразности этапа работ

Отказаться от риска – значит отказаться от творчества.

Александр Сергеевич Пушкин

Как было отмечено выше, ИП отличаются набором специфических рисков, дополняющих стандартные риски инвестиционных проектов. Влияние последних на инновационные проекты по-прежнему остается существенным. Методы их преодоления описаны в большом количестве работ, например [14], и мы не будем на них останавливаться.

Проекты выполняются поэтапно. По этапам выделяется финансирование и подводятся промежуточные итоги. Важно найти критерий, который бы на уровне единичного этапа мог дать раннюю диагностику экономической целесообразности еще до его выполнения, например, в момент принятия решения по техническому заданию. Для этой цели используем предложенный в разделе 4 критерий (3).

Представим ситуацию, при которой некоторый проект достиг уровня готовности N и этот факт подтвержден достоверной экспертной оценкой [2, 10] (Sartori, Ilyina, Mantsevich, 2019; Sartori, Sushkov, Mantsevich, 2020). Не для всех проектов такая ситуация гарантирована. Часть проектов встретит непреодолимые препятствия на пути к коммерциализации, что приведет к их остановке и исключению из портфеля. В этом процессе и находят воплощение основные инновационные риски. Некоторые из них могут реализоваться в полной мере. Тогда проект придется остановить и затраты на подобные проекты потребуется компенсировать из прибыли других проектов. Тем не менее в портфеле останутся проекты с подтвержденными методологией ПИНГ уровнями готовности.

Следуя логике реализации рисков, можно предположить, что до следующего уровня готовности N+1 удастся довести не все проекты, успешно завершившие уровень N. Возникает вопрос: можно ли такие проекты диагностировать заранее, чтобы не тратить на них ресурсы понапрасну? Это позволило бы существенно сократить затраченные средства и повысить выход перспективных для успеха проектов за счет их выборочной поддержки, повысить доходность портфеля. В этом как раз и заключается суть подхода «Бережливый НИОКР» [10] (Sartori, Sushkov, Mantsevich, 2020).

Рассмотрим два этапа оценки перспективных проектов инновационного портфеля. На первом этапе определим экономическую целесообразность продолжения проектов, достигших уровень готовности N, на следующий этап с уровнем N+1. А именно, определим, не затратим ли мы на этом этапе разработки так много средств, что не сможем их компенсировать в процессе коммерциализации.

После отбора проектов уровня N по экономической целесообразности на втором этапе проводится дополнительный отбор проектов по обоснованности перехода на следующий уровень готовности N+1. Отбор проводится с помощью индекса риска, определяемого экспертным путем по критериям ПИНГ для каждого проекта. К этой части отбора привлекаются обученные эксперты, которые работают по определенным данной методикой правилам и метрикам ПИНГ. Второй этап оценки заслуживает отдельного рассмотрения и не является предметом данной статьи.

Вернемся к оценке экономической целесообразности выполнения проекта по предложенному техническому заданию. Возьмем за основу выражение (3): NPV_i * p_i > С_i, которое, как показано выше, определяет экономическую целесообразность проекта.

Для дальнейших преобразований привлечем форму зависимости цены проекта нарастающим итогом C_i(N), где N – подтвержденный уровень готовности, от его уровня готовности (см. раздел 6, далее по тексту зависимость названа «Q-кривая»).

Для каждой организации можно получить данные об усредненной форме Q-кривая кривой, нормированной на цену проекта по предыдущему опыту выполнения работ и их группировке по тематической специфике. Q-кривая показывает доли цены проекта по разным уровням его готовности. Обсуждению формы Q-кривой посвящен следующий раздел, а пока просто примем факт ее существования.

С учетом наличия Q-кривой цена этапа по достижению уровня N+1 будет равна разности C_i (N+1) - C_i(N) = ΔС_i (N; N+1). С другой стороны, ΔС_i= C_i*ΔQ (N; N+1), где ΔQ (N; N+1) – доля стоимости этапа (N; N+1) в полной стоимости проекта, C_i – цена проекта i. Следовательно, оценку полной стоимости реализации проекта можно выразить следующим выражением:

C_i = ΔС_i / ΔQ (N; N+1). (4)

Подставим выражение (4) в неравенство (3). Получим:

NPV_i* p_i > ΔС_i / ΔQ (N; N+1). (5)

Перепишем (5) в более удобном для использования виде:

NPV_i * p_i * ΔQ (N; N+1) > ΔС_{i .} (6)

Выражение (6) представляет базовое условие экономической целесообразности выполнения этапа работ по развитию проекта от уровня готовности N до уровня готовности N+1.

Подчеркнем, неравенство (6) позволяет выделить этапы ИП, поддержка которых экономически целесообразна с точки зрения инновационных рисков, распределения затрат на проект по этапам, планируемой цены этапа и оценки чистого дисконтированного дохода от реализации проекта.

Можно возразить, что повышенную цену какого-либо этапа можно компенсировать за счет снижения цены последующих этапов. С таким подходом можно согласиться, если быть уверенным, что проект будет жизнеспособен и продолжен после следующего этапа. Сам факт наличия рисков достижения положительного результата убеждает нас в том, что такой уверенности не существует. В общем случае нет никаких гарантий, что все проекты, отобранные для развития на уровень N+1, будут поддержаны также для развития на уровень N+2 и далее. Поэтому требование экономической целесообразности должно быть применено к каждому этапу отдельно.

Этот факт отражается уменьшением количества проектов в портфеле по отношению к первоначальному в течение выполнения работ (рис. 1).

На этом можно было бы завершить статью, так как критерий для оценки стоимости этапа по выражению (6) сформулирован. Однако продолжим изложение для тех, кто заинтересован обсудить форму S-и Q-кривых и увидеть, что достижение положительной рентабельности в определенных условиях оказывается инвариантно к их формам, то есть не зависит от их конкретного вида.

6. S- и Q-кривые для уровней готовности проекта

При выводе выражения (6) мы предполагали, что существуют некоторые обобщенные значения p и Q (N) для портфеля проектов. Рассматривая единичный проект, как показывает практика, сложно оценить p_i и Q_i (N; N+1). Однако нет сомнений, что среднестатистически такие величины можно оценить из данных по уже выполненным работам [16, 17]. В дальнейших рассуждениях мы исходили из этого заключения.

Ниже представлены гипотезы о форме S- и Q- кривых и аргументация в пользу их формы. В любой физической теории постулаты не требуют доказательства. Их верность не может быть доказана, но они могут быть оспорены в случае, если экспериментальные результаты противоречат их следствиям. Примем как постулат формы S- и Q-кривых. В относительных единицах эти зависимости представлены на рисунках 2 и 3. На рисунке 2 S-кривая выражает зависимость вероятности успеха (успешной реализации) p проекта от уровня его готовности. Q-кривая выражает долю затрат от полной стоимости разработки на выполнение этапа по достижению уровня готовности N c уровня N-1.

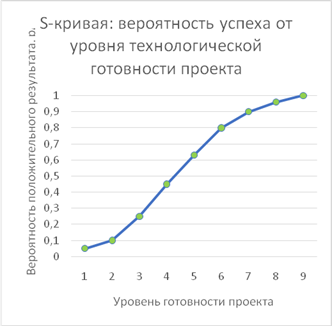Рисунок 2. Зависимость вероятности успеха S от уровня готовности проекта N

Источник: составлено авторами.

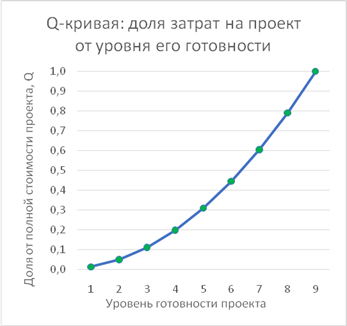
Рисунок 3. Зависимость доли затрат Q от полной стоимости проекта на этап по достижению уровня готовности проекта от N-1 до N

Источник: составлено авторами.

Выражаемые этими кривыми зависимости, их вид имеют важное значение для численных оценок финансовых рисков конкретного инновационного проекта. Сам факт того, что S- и Q-кривые введены в расчет, является определяющим шагом вперед по направлению к решению задачи оценки финансовых рисков. Несмотря на то, что формы этих кривых введены как постулат, они заслуживают того, чтобы о них поговорить подробнее, найдя ответ на следующие вопросы.

1. Существуют ли вообще универсальные S- и Q-кривые?

2. Почему кривые имеют такую форму и каков их математический смысл?

3. Известны ли факты построения обобщенных S- и Q-кривых в литературе?

4. Можно ли изменять форму S- и Q-кривых для некоторых специфических случаев?

Ответим последовательно на эти вопросы.

1. Несомненно, такие зависимости существуют. Для их получения достаточно провести ретроспективный анализ портфеля инновационных проектов организации и произвести соответствующее усреднение по вероятности, бюджету, уровню готовности. Однако для разных по содержанию пакетов проектов и организаций они могут несколько отличаться.

2. Приведем следующие соображения для обоснования выбора формы кривых. Исходя из своей сути, S-кривая является монотонно возрастающей гладкой функцией, при условии, что уровень готовности тоже меняется непрерывно (см. шаги ПИНГ в статье [11]). Авторы не нашли аргументов в опровержение данной гипотезы.

В начале развития инновационного проекта количество и значимость рисков велики. Однако многие из них отрабатываются на ранних стадиях при более полном изучении предметной области проекта. Это приводит на практике к тому, что проекты с реализовавшимися рисками останавливаются, а те, у которых риски не реализовались, продолжаются и вероятность их успешного завершения растет. Поэтому S-кривая на низких уровнях готовности стартует практически из нуля и затем круто растет.

По мере развития проекта продукт обретает все более конкретный облик. В итоге на высоких уровнях готовности S-кривая асимптотически приближается к значению единицы. Начальная и завершающая часть S-кривой соединяются из гипотезы о гладкой функции. Действительно нет никаких оснований для скачкообразных изменений S-кривой.

С формой Q-кривой дело обстоит иначе. На ранних этапах ИП не требует большого количества ресурсов. Исполнители проводят кабинетные исследования. После изготовления макета на третьем уровне готовности к работе подключаются дополнительные компетенции по производству, стратегии патентования, технологии, исследованию рынка. Масштаб работ растет, и после шестого уровня, на котором должен быть подготовлен прототип производственной линии, к проекту подключается потребитель со своими специфическими требованиями и инфраструктурой, в которую нужно вписать экспериментальный образец. Для продукта разрабатывается система поставки комплектующих, контроль качества, система поддержки продаж и послепродажный сервис. По этим причинам общие затраты на проект продолжают расти вместе с крутизной Q-кривой.

Крутизна Q-кривой может изменяться в зависимости от предметной области и является одним из параметров при возможной адаптации предлагаемой методики к конкретным проектам.

3. Было бы наивно считать, что приведенные на рисунках 2 и 3 формы кривых без адаптации будут точно описывать соответствующие зависимости для любых предметных областей и специфических проектов. Адаптация может быть проведена тремя путями на выбор пользователей.

Первый заключается в формировании кривых с использованием статистики предыдущих работ организации – разработчика продукта проекта.

Второй – в экспертном задании формы кривых для конкретного портфеля проектов.

Третий – в использовании представленных на рисунках 2 и 3 кривых как стартовой точки для последующих итераций по мере накопления статистики в конкретной организации. Этот вариант адаптации принят нами за базовый.

Однако при перечисленных выше вариантах адаптация в большинстве случаев будет заключаться в небольшой модификации их параметров при сохранении общей формы, представленной на рисунке 2.

4. Форма зависимости вероятности реализации и цены этапов работ, полученные статистическим анализом представительной базы проектов, приведены в работах [16] и [17]. Формы S- и Q-кривых из приведенных примеров находятся в полном соответствии с рисунками 2 и 3, что подтверждает принятые нами допущения, положенные в основу гипотезы о форме этих кривых.

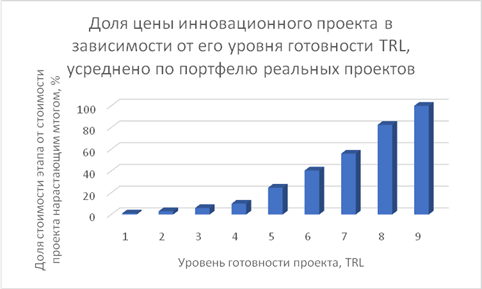
Рисунок 4. Пример формы Q-кривой доли стоимости этапов от полной стоимости проекта (для проектов вооруженных сил США)

Источник [17].

Исходя из этого, мы используем данные формы зависимости вероятности в методике оценки финансовых рисков, понимая, что впоследствии после набора достаточного массива практических данных эти формы можно легко адаптировать под специфику каждого портфеля проектов, повысив тем самым точность прогноза. Методику и алгоритмы расчета рисков при этом менять не требуется.

7. S-кривая для параметров инновационной готовности ПИНГ

В работе [11] (Sartori, Gareev, Ilyina, Mantsevich, 2020) показаны шесть групп рисков – параметров инновационной готовности (ПИНГ), которые имеют различную природу.

Если по метрике TRL в публикациях можно найти статистику по зависимости рисков от уровня готовности [16], то по MRL, IRL, ORL, BRL и CRL таких зависимостей найти не удалось. Это понятно: тема численного описания рисков в методологии уровней готовности новая, и достаточная статистика еще не собрана.

Вместе с тем очевидно, что механизм действия непредвиденных обстоятельств (рисков) для всех ПИНГ не различается кардинально. По мере того как при реализации проекта сужается область его цели (ценностное предложение), становится проще в нее попасть. Вместе с этим снижается количество и значимость рисков. Поэтому в первом приближении форму S-кривой на рисунке 2 можно использовать не только для TRL, но и для уровней готовности MRL, IRL, BRL, ORL, CRL, с уточнением, что кривая будет более пологой (рис. 5). Причина заключается в том, что технологические риски являются наиболее значимыми и непредсказуемыми.

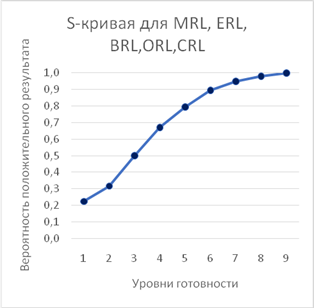
Рисунок 5. Пример формы S-кривой метрик MRL, IRL, BRL, ORL, CRL

Источник: составлено авторами.

Несмотря на приведенные выше аргументы и соображения, можно возразить, что S- и Q-кривые могут отличаться от «идеальных кривых» и проводить подобные оценки невозможно. Однако практический менеджмент придерживается иной точки зрения. Идеальное решение – враг практического решения. Лишь практические решения приводят к действию [18] (Dzho Ouen, 2011).

8. Расчет интегральной вероятности положительного результата

Отметим следующее обстоятельство: поскольку присущие ПИНГ риски имеют принципиально разную природу, то влияние их на суммарную вероятность положительного результата p_i в выражении (6) по законам статистики будет определяться их произведением.

В таблице 1 постулированы модельные значения вероятности успеха для уровней готовности, определяющие S-кривые для каждого из ПИНГ.

Таблица 1

Значения вероятности успеха проекта раздельно по ПИНГ в зависимости от уровня готовности, принятые в качестве модельных для расчетов

Рассмотрим процесс вычисления вероятности p_i по всем ПИНГ на примере третьего уровня готовности. Подставляя величины частных вероятностей из таблицы 1 для каждого ПИНГ, получим:

P_i(3) = 0,25*0,5*0,5*0,5*0,5*0,5 = 0,0078 – для проектов, в которых все шесть ПИНГ являются критическими (далее по тексту – 6-ПИНГ проекты), то есть риски выполнения которых существенно влияют на успешную реализацию проекта;

P_j(3) = 0,25*0,5*0,5 = 0,063 – для проектов по созданию программного обеспечения, в котором критическими являются три ПИНГ: TRL, ORL, CRL (далее по тексту – 3-ПИНГ проекты).

Данное значение вероятности показывает, что на третьем уровне готовности совокупность рисков все еще значительная. В итоге из десяти тысяч проектов в области создания различного назначения оборудования и установок до успешной реализации в среднем доходят четыре проекта, а в области программного обеспечения – 1–2%. Такая статистика подтверждается опытом [5].

Для шестого уровня готовности картина с итоговым риском меняется.

P_i(6) = 0,8*0,89*0,89*0,89*0,89*0,89 = 0,45 – для проектов, в которых все ПИНГ являются критическими, то есть риски выполнения которых существенно влияют на успешную реализацию проекта, например создание приборов, установок.

P_j(6) = 0,8*0,89*0,89 = 0,63 – для проектов по созданию программного обеспечения, в котором критическими являются три ПИНГ: TRL, ORL, CRL.

Такие значения вероятностей не должны быть неожиданными. Опыт венчурных фондов говорит о невысокой доле успешно реализованных проектов [4].

Этот результат оценки рисков на разных уровнях готовности является еще одним аргументом в пользу того, что неотъемлемым элементом бережливого НИОКР как части любой инновационной разработки является не равномерное распределение средств на поддержку всех проектов портфеля, а отбор наиболее перспективных, в том числе с использованием оценок согласно выражению (6).

Несмотря на то, что наименьший риск развития имеет проект с равномерным развитием по всем ПИНГ (принцип бережливого НИОКР), на практике могут встречаться примеры, когда уровни готовности в ходе разработки инновационного продукта для различных ПИНГ будут разные.

В такой ситуации можно оценить вероятность достижения результата для 6-ПИНГ проектов следующим образом:

P_i(N) = S_TRL(N₁)*S_MRL(N₂)*S_ERL(N₃)*S_ORL(N₄)*S_BRL(N₅)*S_CRL(N₆) , (7)

где S_TRL(N₁), S_MRL(N₂), S_ERL(N₃), S_ORL(N₄), S_BRL(N₅), S_CRL(N₆) – значения вероятности на S-кривых для соответствующих ПИНГ и подтвержденных для них уровней готовности N_k, k = 1-6.

В силу того, что условия достижения уровней готовности по разным ПИНГ являются согласованными, то достижение части ПИНГ более высоких уровней готовности может нести риски их неверной интерпретации. По этой причине для 6-ПИНГ проектов более консервативной будет следующая оценка вероятности реализации:

Pi(N) = S_TRL(N_min)*S_MRL(N_min)*S_ERL(N_min)*S_ORL(N_min)*S_BRL(N_min)*S_CRL(N_min), (8)

где N_min – минимальное значение уровня готовности по всем используемым в проекте ПИНГ.

Специфика некоторых проектов такова, что не все ПИНГ требуются для описания рисков. Например, если продукт предполагается только для внутрикорпоративного использования, то есть процедура внедрения и заказчики определены, то ORL и CRL могут не применяться или быть адаптированы. Так, в экономическом обосновании для внутреннего применения целесообразным вместо рыночных секторов TAM, SAM, SOM использовать данные об объеме внедрения инновационного продукта в отрасли и на предприятии.

Если продукт будет производиться на существующей производственной линии, то использование MRL можно опустить. Если продукт не интегрирован в систему, а используется самостоятельно, то IRL можно не принимать во внимание.

Решение о подтверждении уровней готовности проекта, выборе применимых ПИНГ, декомпозиции продукта на элементы, выделении критических элементов, прогнозе NPV, оценке верхней границы стоимости этапов и приобретаемых проектов/технологий должна решать уполномоченная группа специалистов, владеющих методологией ПИНГ.

По данным таблицы 1 можно построить вероятности достижения положительного результата для проектов по разработке оборудования и программного обеспечения (рис. 6).

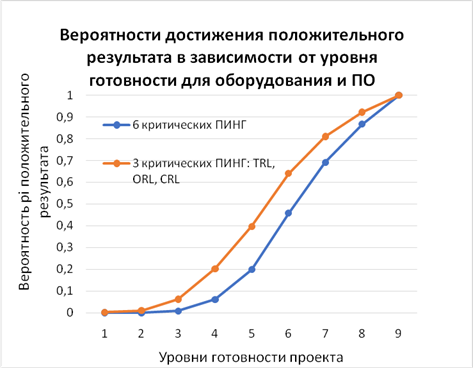
Рисунок 6. Вероятности достижения положительного результата для проектов по разработке оборудования и программного обеспечения Источник: составлено авторами.

Как мы отмечали ранее, на практике количество успешно реализованных IT-проектов превышает количество успешных hardware-проектов, что находится в соответствии c данными, представленными на рисунке 6 для 3-ПИНГ проектов.

9. Примеры расчетов по методике

Применим описанную выше модель для иллюстрации оценки экономической эффективности при управлении портфелем проектов, приняв следующие допущения:

1. Задача управления портфеля – обеспечить успешную реализацию M = 5 проектов.

2. 80 проектов одобрено на уровне готовности 3 (см. пример на рис. 1).

3. Все проекты однотипны, и каждый имеет NPV = 200 млн руб.

4. Проекты имеют три критических ПИНГ: TRL, ORL, CRL, кривая рисков описывается верхней кривой, показанной на рисунке 6.

5. Q-кривая соответствует кривой на рисунке 8а, соответствующей условию: «Непредсказуемость и значимость рисков нормальные».

6. Чистый дисконтированный доход от реализации M = 5 успешных проектов составит M*NPV = 1000 млн руб.

7. NPV не включает затраты на разработку проекта до девятого уровня готовности.

Максимальные затраты на выполнение этапа (N; N+1) для одного проекта согласно выражению (6) составят NPV_i* p_i*ΔQ(N; N+1).

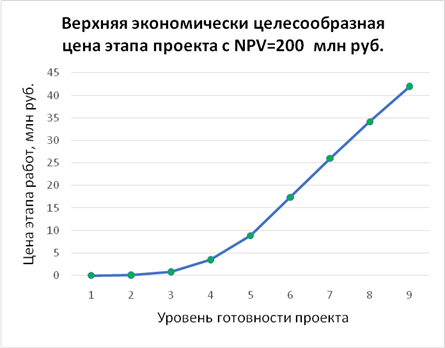
Рисунок 7. Оценка верхней экономически целесообразной цены этапа проекта в зависимости от уровня его готовности. Расчет проведен по выражению (6): NPV_i*p_i*ΔQ (N; N+1) = ΔСi для перехода с уровня N на уровень N+1

Источник: составлено авторами.

Из данных рисунка 7 следует, что экономически нецелесообразно в данном портфеле поддерживать проект по развитию продукта, например с уровня готовности 5 на уровень 6, с ценой этого этапа 9 млн рублей и более, а с уровня готовности 6 на уровень 7 при цене этапа более 17 млн рублей.

В модельном расчете определялись суммарные максимальные затраты на каждый этап разработки для всех M проектов, а затем затраты суммировались по всем девяти уровням готовности. По определению вероятности положительного результата число проектов, оставленных в портфеле на уровне готовности N, равно M/pi(M). Соответственно, для значения M проектов затраты составят:

(M/p_i(M))*NPV* p_i*ΔQ (N; N+1) = M*NPV*ΔQ (N; N+1).

Параметр p_i в формуле сокращается, а сумма затрат по всем уровням готовности составит:

(9)

Далее, учитывая, что M и NPV являются константанами, а =1, из выражения (9) следует, что сумма затрат по всем этапам по портфелю проектов равна .

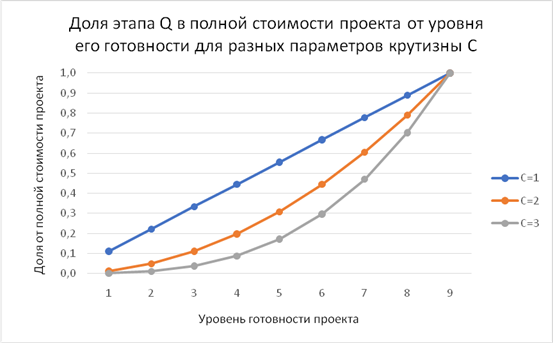
Мы пришли к очень важному выводу о том, что независимо от форм S- и Q-кривых (примеры показаны на рисунке 8(а) и (б)) при управлении портфелем идентичных проектов по описанной методике затраты равны доходу, и безубыточность портфеля будет обеспечена. Обратим внимание, что безубыточность портфеля обеспечивается даже с учетом невозвратных затрат на замороженные проекты.

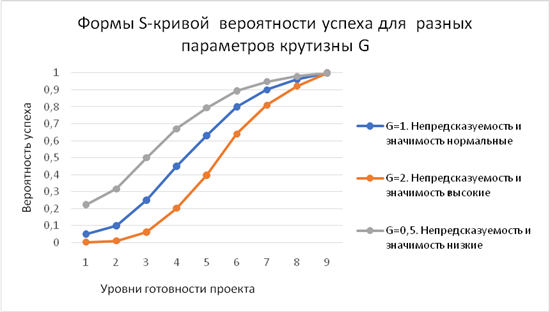
а)

б)

Рисунок 8. Примеры различных возможных форм зависимости вероятности успеха (а) и удельной стоимости этапов проекта (б) от уровня готовности проектов

Источник: составлено авторами.

Чем больше будет значение левой части неравенства (6) его правой части, тем больше будет рентабельность портфеля проектов.

С учетом полученных результатов по предельной стоимости этапов была рассчитана динамика общих затрат на выполнение портфеля проектов по уровням готовности. Результаты расчетов показали, что общие затраты на весь портфель проектов в рассматриваемых ограничениях линейно зависят от уровня готовности (рис. 9).

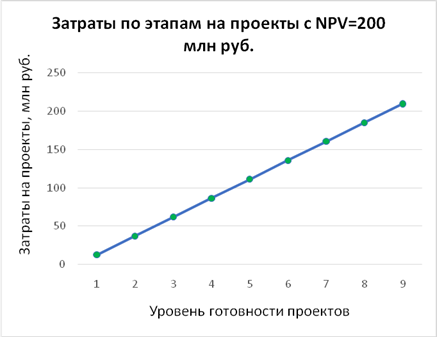
Рисунок 9. Затраты на портфель проектов по уровням готовности в условиях прекращения финансирования остановленных высокорисковых проектов по методике бережливого НИОКР

Источник: составлено авторами.

Факт инвариантности методики безубыточного управления портфелем проектов по отношению к формам S- и Q-кривых, величине NPV, числу проектов говорит о том, что данный результат будет справедлив не только для модельного расчета из М = 80 (допущение 2 в разделе 9) одинаковых проектов, но и при разнородном составе портфеля с наличием групп разного числа однотипных проектов, отличающихся по формам S- и Q-кривых, а также величине NPV.

Таким образом, методика позволяет определять условия и осуществлять безубыточное управление реальными портфелями инновационных проектов.

10. Оценка стоимости покупки ИП на ранней стадии

Не рискуй понапрасну и действуй наверняка.

Эрих Мария Ремарк, «Триумфальная арка»

В практике организаций могут встречаться потребность в покупке инновационных проектов/технологий на ранней стадии готовности.

Для расчета стоимости покупки потребуется оценка NPV и вероятность реализации проекта для экспертно подтвержденных уровней готовности по всем ПИНГ согласно выражению (10).

_, (10)

где C_x – цена предполагаемой покупки проекта х;

Nmin – минимальное значение уровня готовности по всем ПИНГ;

Pх – вероятность реализации проекта по формуле (8) для S-кривых с аргументом Nmin.

– доля стоимости доработки проекта до уровня готовности 9.

Таким способом определенные условия стоимости покупки инновационного проекта соответствуют минимизации риска инвестора для любого уровня готовности разрабатываемого в приобретаемом проекте продукта и могут быть использованы в том числе для рынка открытых инноваций.

11. Заключение

На основе методологии ПИНГ предложена методика управления рисками ИП, включая технологические и финансовые риски инвестиций, в том числе на начальных высокорисковых стадиях исследований и разработок.

На модельном примере показано, что методика оценки экономической эффективности выполнения этапов является инвариантной к форме рисков, удельной стоимости этапов работ, числу проектов в портфеле, величине NPV. По этой причине методика может применяться к широкому классу портфелей, в том числе разного состава, проектам из разных предметных областей.

Обеспечение положительной рентабельности портфеля проектов возможно при следующих условиях:

· подтверждение уровня готовности на каждом этапе по методике ПИНГ;

· экспресс-анализ и выделение экономически целесообразных этапов;

· экспертное ранжирование этапов проектов по научно-техническим и инновационным рискам по метрикам ПИНГ;

· поддержка финансирования фиксированной доли проектов с учетом S- и Q-кривых.

Критерий экономической целесообразности можно использовать при определении цены ИП ранних стадий на рынке открытых инноваций.

Предложенная методика может служить практической основой для целенаправленного повышения эффективности научных разработок, установления предметного взаимодействия разработчиков инновационных продуктов с промышленностью.

[1] В статистической физике такой подход применяется для замены анализа изменения параметров одной выделенной частицы во времени на анализ моментального распределения этих параметров по набору частиц – ансамблю [13].

[2] В силу ограниченности объема выборки M мы оцениваем выборочное среднее, которое, однако, стремится к истинному значению математического ожидания при стремлении M к бесконечности.