Математические модели и алгоритмы интеллектуальной платформы нового типа для реализации индивидуальной траектории обучения с учетом психотипа обучающегося

1. Введение

Вынужденный переход в связи с пандемией на тотальное дистанционное обучение обнаружил достаточно низкую степень готовности цифровых образовательных платформ. Решение возникших проблем возможно только за счет кардинального пересмотра концепции цифрового образования, разработки методически обоснованных и индивидуальных подходов к онлайн-преподаванию различных учебных курсов, учета индивидуальных особенностей и интересов как обучающихся, так и преподавателей, создания новых образовательных платформ и качественной проработки используемого методического материала. На решение указанных проблем направлено данное исследование.

Цель исследования: разработка концепции, математических моделей и алгоритмов интеллектуальной образовательной платформы (ИОП) нового типа, направленной на самостоятельное усвоение студентом заданных дисциплин, осуществляемое в процессе взаимодействия с электронной обучающей системой, подстраивающейся под уровень знаний студента, его психотип, систему предпочтений и индивидуальные особенности нервной системы, а также обеспечивающей объективный контроль за уровнем освоения результатов в плане компетентносто-ориентированного подхода.

Разработанная концепция направлена на решение задач:

1) спроектировать и разработать методически обоснованный электронный курс (ЭК) (на примере высшей математики), обеспечивающий полноценное изучение предмета без прямого участия преподавателя, осуществляемое на основе концепции программированного обучения;

2) разработать концепцию учета психотипа студента в ЭК посредством методов геймификации и создания интерфейса, отвечающего основным психотипам в соответствии с классификацией Бартла;

3) разработать нечетко-множественную математическую модель подстройки ЭК под уровень знаний студента, его психотип и индивидуальные особенности нервной системы студента на основе системы нечетко-логических выводов (продукционных правил);

4) разработать методику настройки системы нечетко-логических правил, управляющих ЭК, на основе результатов тестирования контрольных групп студентов посредством как классических, так и вновь разработанных тестов;

5) разработать нечетко-множественную модель оценки результатов обучения студента с использованием компетентносто-ориентированного подхода;

6) разработать программный комплекс, реализующий ИОП.

Предполагаемый итоговый теоретический результат: разработка принципиально новой ИОП, объединяющей в себе классические методы программированного обучения и геймификацию, направленную на создание индивидуально-ориентированной образовательной среды и обеспечивающей наиболее эффективное и комфортное взаимодействие человека с электронной системой, а также обеспечивающей объективный контроль за уровнем результатов образовательной деятельности.

2. Материалы и методы

Предлагаемая ИОП должна состоять из следующих трех блоков, реализуемых на основе математических моделей, методов и программных средств: 1) электронных курсов (ЭК), созданных на основе программируемого обучения; 2) оболочки, представляющей собой веб-форму, осуществляющую подстройку под психотип студента и реализованную на основе подхода геймификации; 3) блока контроля за уровнем достигнутых результатов на основе компетентностно-ориентированного подхода.

2.1. Программируемое обучение

За основу ЭК предполагается взять программируемые учебники и пособия, относящиеся к реализованному в 1970–80-х годах кибернетическому подходу, осуществляющему обучение студента по индивидуальной траектории, и в полной мере охватывающие современный курс математики, линейной алгебры и математического анализа. Для обеспечения унифицированного и методически обоснованного текущего контроля успеваемости предлагается разработать рейтинговую систему начисления баллов как за прохождение ЭК, так за итоговое тестирование.

Концепция программированного обучения возникла в начале 50-х гг. XX в., когда американский психолог Беррес Скиннер (1904–1990) предложил повысить эффективность усвоения материала, выстраивая его как последовательную программу подачи порций информации и контроля за их усвоением [1, 2] (Selevko, 1998; Hoškova, 2009). Программированное обучение – обучение по специально разработанной обучающей программе, которое представляет собой определенную последовательность конкретных задач, путем которых выполняется и контролируется деятельность педагога и учащихся.

Программируемое обучение было позитивно воспринято научным сообществом СССР. В разработке концепции программируемого обучения активно участвовали такие ученые, как Н.Ф. Талызина, П.Я. Гальперин, Л.Н. Ланда, И.И. Тихонов, А.Г. Молибог, А.М. Матюшкин, В.И. Чепелев, И.Е. Шварц и другие [3, 4] (Talyzina, 1969; Bespalko, 1970). В 70–80 годы программируемое обучение широко внедрялось в учебный процесс в отечественных вузах, в первую очередь технических. Однако кибернетический подход, на который было ориентировано программируемое обучение, не был реализован в силу отсутствия необходимой материальной базы. В настоящее время в связи с достаточным развитием компьютерных технологий и дистанционного обучения в отечественной педагогике происходит возрождение интереса к программированному обучению в образовательной практике [5–8] (Marushina, Bystrov, 2009; Mukhamedshina, 2012; Malyhina, 2002; Martirosyan, 2010). В англоязычной литературе можно встретить примеры ограниченного применения программируемого обучения (чаще используется термин «программируемые команды») в первую очередь для обучения языкам программирования [9] (Vargas Julie, 2014).

Препятствиями на пути активного использования подхода, на наш взгляд, является: 1) практическая сложность реализации программируемого обучения; 2) недоверие педагогического сообщества к «обучению людей машинами», полемика по поводу неучета эмоциональной компоненты обучения и личных особенностей студентов.

Первое препятствие может быть преодолено за счет обращения к методическим разработкам 70–80-х годов, которые еще сохранились в архивах и на кафедрах «старых» технических вузов. Указанные разработки представляют собой большую методическую и научную ценность, поскольку создают предпосылку для прорыва в применении программируемого обучения в цифровом образовании. Их поиск, восстановление и перевод в «цифровой» формат представляет собой серьезную и не терпящую отлагательства задачу. Второе препятствие может быть также преодолено за счет новых технологий вычислительной техники, приведшей к возникновению и быстрому развитию нового подхода в обучении – так называемой геймификации.

2.2. Геймификация обучения как образовательный подход, учитывающий индивидуальные особенности студента

Геймификация – это технология адаптации игровых методов к неигровым процессам и событиям для большей вовлеченности сотрудников/участников в процесс. В настоящее время существует развитая теоретическая база применения геймификации в обучении [10–13] (Orlova, Titova, 2015; Pevzner, Pogorelov, Shuklin, 2016; Eliseeva, Zyateva, Isakova, Kiyutina, Shkityr, 2016; Titov, 2013). В качестве рычагов влияния на участников процесса применяются следующие элементы. Баллы – вознаграждения, получаемые за совершение определенных действий в каком-либо процессе. Бейджи – виртуальные награды, предназначенные для измерения активности участников процесса. Рейтинги – показатели, отображающие успехи участников процесса. Уровни – статусы, которых участники могут достигать посредством своих действий в процессе. Лидерборды – таблицы лидеров, на которых обозначаются участники-лидеры. Виртуальная валюта – средства, которые можно зарабатывать и тратить в виртуальных точках продаж. Виртуальные товары – товары, которые можно покупать на виртуальные деньги. Интерактивные элементы – всевозможные элементы визуализации процесса. Дайджесты успеха – тематические информационные продукты. Указанные элементы могут применяться как унифицированно, так и с учетом психологических особенностей игрока, определенных на основе существующих классификаций, например Ричарда Бартла. Вот какие типы игроков описывает Ричард Бартл.

· Накопители (Achievers) или карьеристы, для которых важно накопление мощи, денег, артефактов – любых игровых благ и ресурсов.

· Киллеры (Killers), для которых главная мотивация – превосходство над другими игроками, доминирование, властвование.

· Исследователи (Explorers), которым интересно изучать игровой мир.

· Социальщики (Socializes) или тусовщики, для которых важно общение с другими игроками, социальное взаимодействие и взаимопонимание.

В приложении к ИОП мы предлагаем создать систему управления оболочкой системы, реализующую индивидуальный подход к обучающимся на основе геймификации и системы психотипов Бартла. Осуществлять подстройку предлагается на основе программного блока нечетко-множественных моделей. Предполагается использование традиционных инструментов геймификации, таких как рейтинги и лидерборды, монетизация достижений, доступ к библиотекам, общение в чатах и социальных сетях, для активизации в обучении движущих сил, присущих психотипам достигателя, накопителя, исследователя, социализатора. Этот подход позволит положительно замотивировать в достижении более высоких результатов в учебе не только студентов-исследователей и студентов-достигателей (что характерно для классической педагогики), но также и накопителей с социализаторами.

2.3. Компетентностно-ориентированный подход

Компетенции – базовые качества индивидуума, имеющие причинные связи с эффективной деятельностью после обучения [14] (Chelyshkova, 2012). В психолого-педагогической литературе понятия «компетенция» и «компетентность» получили широкое распространение с середины 60-х гг. прошлого века, став основой становления компетентностного подхода в образовании (Уотсон, Торндайк, Скиннер, Тайлор, Блум, Н. Хомский, Р. Уайт, Дж. Равенн, Ж. Делор, В. Хутмахер, Т. Хоффманн). В России проблематикой компетентностного подхода по отношению к различным видам деятельности занимаются В.И. Байденко [15] (Baydenko, 2006), И.А. Зимняя [16] (Zimnyaya, 2006), А. Каспржак [17] (Kasprzhak, 2005), В. Ландшеер [18] (Landsheer, 1988), А.К. Макарова [19] (Makarova, 1990), Н.С. Сахарова [20] (Sakharova, 1999), Ю.Г. Татур [21] (Tartur, Medvedev, 2007), А.В. Хуторской [22] (Khutorskoy, 2003) и др.

В работе [23] (Morcke, 2013) утверждается, что «образование, основанное на результатах, и образование, основанное на компетенциях, в основном сосредоточены на продукте, а не на процессе, любые различия между ними незначительны». Компетенция определяется как «результат комплексного обучения, в котором навыки, способности и знания взаимодействуют, образуя наборы» и которые имеют ценность по отношению к задаче, для которой они собраны [24] (Jones, Voorhees, 2002).

Компетентностный подход к образованию соответствует Tuning Educational Structures («Настройка образовательных структур в Европе»), который был инициирован в 2000 году [25] (Gonzalez, 2008).

Для отечественного образования данный подход не является чем-то новым. Ориентация на усвоение умений, способов деятельности и, более того, обобщенных способов действия была ведущей в работах отечественных педагогов и психологов еше до внедрения компетентностного подхода к образованию (В.В. Давыдов, В.В. Краевский, Н.В. Кузьмина, И.Я. Лернер, М.Н. Скаткин, Г.П. Щедровицкий и др.). Однако в настоящее время его формализация требует дополнительных исследований в заданном направлении. В первую очередь в разработке нуждается методика оценивания степени сформированности компетенций у студента с учетом особенностей и традиций отечественного образования [14] (Chelyshkova, 2012).

Компетенции разлагаются на результаты обучения по отдельным дисциплинам, которые проверяются в ходе аттестации – текущей, промежуточной, итоговой (тесты, контрольные работы, устные опросы, курсовые работы и т.д.). Результаты обучения соответствуют отдельным уровням (этапам) и аспектам (элементам) компетенций и сопоставимы с конкретными составляющими учебного плана (дисциплинами, практиками, НИР, самостоятельной работой и т.п.). Результаты обучения являются описанием знаний, умений и навыков (владений) студента после успешного завершения определенного этапа обучения. Результаты обучения представляют собой параметры, которые могут быть измерены и достижение которых является подтверждением того, что запланированные компетенции сформированы.

Таким образом, отечественный компетентностно-ориентированный подход представляет собой современное переосмысление существовавшего подхода к подготовке специалистов в рамках плановой экономики. Такой подход основан на четко сформулированных и обоснованных требованиях, структурирован, имеет разработанную нормативно-правовую базу. Особое внимание в нем уделяется настоящей разработке и научному обоснованию оценки результатов обучения. Разработанный на данный момент подход к оцениванию уровня сформированности компетенций состоит в многоступенчатых критериально-ориентированных измерениях, позволяющих получить обоснованные оценки [14] (Chelyshkova, 2012).

Для оценки компетенций разработан целый ряд оценочных средств, таких как деловая и/или ролевая игра; кейс-задача; коллоквиум; контрольная работа; круглый стол, дискуссия, полемика, диспут, дебаты; портфолио; проект; рабочая тетрадь; разноуровневые задачи и задания; расчетно-графическая работа; реферат; доклад, сообщение; собеседование; творческое задание; тест; тренажер; эссе и т.д. Для каждого вида оценочного средства имеются характеристики, нормативы представления в фонде оценочных средств, а также система градаций для выставления оценки. Устанавливаются соответствия между видами оценочных средств и уровнями оценки овладения компетенцией [14] (Chelyshkova, 2012).

Следует, однако, заметить, что большинство предлагаемых методов оценки компетенций достаточно сложны и требуют значительных временных затрат для применения на практике. Можно выделить следующие проблемы.

Во-первых, для оценки каждой из компетенций (либо их кластера) требуется составлять свой набор заданий и, таким образом, кардинально пересматривать уже существующие средства оценки. Между тем в настоящее время на большинстве профилирующих кафедр существует детально разработанная методическая база (банки тестов, вопросы к собеседованию, коллоквиуму, зачету, экзамену, индивидуальные и типовые задания и т.п.), в целом пригодная для оценки профессиональных компетенций. Во-вторых, процесс оценки каждого кластера компетенций должен осуществляться отдельно, причем в несколько этапов. В-третьих, при таком подходе требуется разрабатывать сложную систему начисления баллов за каждое задание, продумывать распределение баллов между оценочными средствами. При этом малейшее изменение структуры заданий, добавление либо исключение одиночного средства оценки приводит к необходимости заново пересчитывать всю систему оценки. В-четвертых, балльная система оценки компетенций часто приводит к ситуации, когда недобрав один-два балла, студент получает неоправданно низкую аттестационную оценку. Все это указывает на необходимость совершенствования существующих подходов в сторону их упрощения, адаптации под уже существующие фонды оценочных средств и проверенные десятилетиями методы проверки знаний.

Мы предлагаем модифицированный подход к оценке уровня сформированности компетенций, основанный на теории нечетких множеств, универсального математического аппарата, позволяющий учесть неопределенность экспертных оценок и приблизиться к решению перечисленных проблем.

3. Практическая реализация блоков ИОП

3.1. Реализация программируемого обучения в ИОП

Методика апробирована на материале раздела курса высшей математики «Векторная алгебра». При составлении курса использованы следующие материалы [26–28] (Kachanova, 1976; Kostina, 2009). Нами предложена адаптация методики дифференцированного обучения математике Костиной Е.А. [27] (Kostina, 2009) к электронному курсу, реализованному на примере раздела «Векторная алгебра» с использованием источников [26, 28] (Kachanova, 1976). Методологической основой являются [27] (Kostina, 2009): 1) дифференцированный подход к процессу обучения (Г.Д. Глейзер, И.М. Осмоловская, И.Э. Унт); 2) структурный подход к изучению математических способностей (И. Верделин, В.А. Крутецкий, Н.А. Менчинская, Э. Торндайк, Ч. Спирмен, И.С. Якиманская); 3) деятельностный подход к процессу обучения (Л.С. Выготский, А.Н. Леонтьев, С.Л. Рубинштейн).

В соответствии с методикой Костиной Е.А. [27] (Kostina, 2009), для раздела «Векторная алгебра» предлагается два тестирования: входное и выходное. Входное тестирование строится на материале предшествуюшего раздела «Линейная алгебра». Выходное тестирование осуществляется на материале проходимого раздела «Векторная алгебра». Оно же является входным для следующего раздела «Аналитическая геометрия». Методика диагностирования подробно описана в главе 2 диссертации Костиной Е.А. (стр. 116–122) и может быть реализована в ПО.

После прохождения студентом тринадцати диагностических циклов преподаватель обладает информацией об уровне развития каждого компонента его математических способностей. В результате студент может быть отнесен к одной из групп, перечисленных в таблице 1.

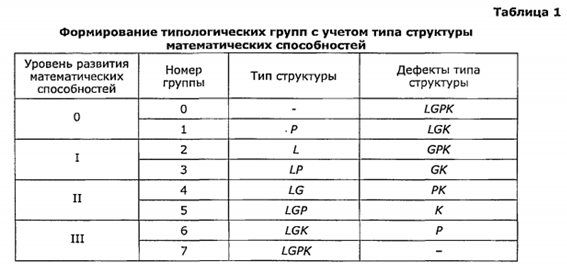
Здесь: L – логичность мышления; G – гибкость; K – креативность; P – пространственное мышление. Каждая типологическая группа характеризуется, с одной стороны успешностью решения блоков задач, отраженных в типе структуры математических способностей, и с другой – неудачами в решении остальных блоков, которые объясняются наличием дефектов типа структуры способностей. Подробное описание групп, их успешных сторон, дефектов и предпочтительных подходов обучения приведено в [27] (Kostina, 2009).

На основе характеристик групп нами были выделены четыре основных подхода к подаче материала на практических занятиях: группы 0–1 – разобрать решение подробно, дать образец; группы 2–3 – дать систему задач, подсказку и т.п.; группы 4–5 – подсказка на уровне плана; группы 6–7 – решить самостоятельно. Очевидно, что соседние группы, входящие в одну пару, отличаются друг от друга лишь большим/меньшим уровнем пространственного мышления. Соответственно, в группах, где пространственное мышление менее развито, изложение должно осуществляться наглядно (динамические чертежи). Подача материала в группах должна осуществляться с учетом их сильных сторон, с одной стороны, и в расчете на развитие/компенсацию недостающих способностей, с другой.

«Лекция» (то есть теоретический материал с задачами самоконтроля) – единая для всех групп. При этом имеются варианты ее визуального и аудиального восприятия; настройка осуществляется на основе нечетко-множественных команд, как это будет рассмотрено ниже, для геймификации. Изложение теории, сопровождаемое решением закрепляющих примеров, построено по принципу программируемого обучения и остается в целом неизменным для всех восьми групп. Однако предполагается, что ряд относительно сложных и обьемных доказательств будет скрыт для групп 0–1-2–3. При этом у них в курсе соответствующее место помечается символом «факультативный материал». Иллюстративный материал частично варьирован по группам в соответствии со способностью воспринимать материал.

«Практика» (то есть решение практических задач) проводится по индивидуальной траектории в соответствии с номером группы.

Из единого банка задач (тестов различного типа) для каждой группы выбирается свой набор задач по теме. Например, по теме «Скалярное произведение» для групп 0 и 1 набор задач представляет собой варьирование заданий на нахождение угла, проекции, работы, проверку перпендикулярности векторов. Для групп 2–3 соответствующий набор задач направлен на беглый проход по задачам данного уровня с последующим решением задач на геометрические фигуры, а также нахождение вектора по условиям. Для групп 4–5 работа начинается непосредственно с решения задач на геометрические фигуры, после чего идет отработка решения задач на нахождение вектора по заданным условиям с заключительным решением двух-трех нестандартных задач. Работа в группах 6–7 состоит из разминки в виде решения трех-четырех задач на геометрические фигуры, блока задач на нахождение вектора с варьированными условиями, усложненных, а также нестандартных задач.

Задачи оформлены в виде тестов; при этом за решение каждой задачи начисляются баллы в зависимости от сложности и полноты решения.

По каждому подразделу осуществляется итоговое тестирование, за которое студент набирает баллы. Студент также набирает баллы в процессе работы с теоретическим материалом (задания самоконтроля) и на «опросах теории» (в виде тестирования). По прохождении всего раздела студенту начисляется итоговая сумма баллов. Переход к следующему разделу возможен, если сумма набранных баллов не менее 60% от максимальной.

Таким образом, ставится «планка» для перехода к следующей теме, преодолеть которую можно, решив верно достаточное количество задач. Если у студента по какой-либо причине не получается набрать баллы внутри своей группы, он может нажать кнопку, соответствующую переходу в низшую группу. Аналогично в случае успешного работы студент имеет право, наоборот, перейти в группу высшую.

3.2. Реализация геймификации в ИОП

Реализация подстройки ИОП под психотип пользователя реализуется посредством психотипно-ориентированных вкладок. Так, вкладка «Уровень достижений» ориентирована в первую очередь на «достигателей»; вкладка «Общение» ориентирована на «социальщиков»; вкладка «Информация» ориентирована на «исследователей». Однако практически каждый пользователь (здесь – студент) представляет собой комбинацию нескольких психотипов, поэтому каждая из вкладок должна быть развернута для каждого пользователя с учетом его потребностей. В соответствии с этом предложено для каждой из вкладок разработать три уровня: базовый (1), развернутый (2) и психотипно-ориентированный (3).

Предлагается на каждой вкладке ввести автоматическую систему начисления баллов при обращении. Причем накопление баллов осуществляется так, что различные действия оцениваются различным количеством баллов. Например, за простой выход на форум начисляется 1 балл. За участие в обсуждении проблемы – 2 балла. За приглашение в группу друга – 5 баллов и т.д. После этого устанавливается соответствие между уровнями интерфейса и количеством баллов, накопленных пользователем за оцениваемый период, на основе экспертных оценок. Для установленных таким образом диапазонов вычисляются центры тяжести, и на их основе формируются нечеткие множества: SX1 = «социальная активность малая», SX2 = «социальная активность средняя», SX3 = «социальная активность высокая». После этого формируются правила нечеткой продукции (теория нечетких множеств [29] (Konysheva, Nazarov, 2011)) для выбора интерфейса вкладки «Общение».

Аналогично на основе анализа статистики работы со вкладками «Уровень достижений» и «Информация» формируется их интерфейс.

Пример подстройки приложения под психотип в соответствии с типологией Бартла на основе правил нечеткой продукции

Этап 1. Обработка экспериментального материала с целью выделения экспертных групп. Пусть результаты тестирования студентов представлены группой из 100–120 человек по тесту Бартла. Установлено, что в контрольной группе количество человек:

а) достигатель (в нем объединены такие психотипы, как накопитель и киллер): 30 – ярко выраженный достигатель; 65 – средне выраженный достигатель; 25 – слабовыраженный достигатель;

б) социальщик: 32 – ярко выраженный социальщик; 58 – средне выраженный социальщик; 10 – слабовыраженный социальщик;

в) исследователь: 20 – ярко выраженный исследователь; 64 – средне выраженный исследователь; 16 – слабовыраженный исследователь.

По данным а, б, в, исходную группу разбивают на экспертные группы. В каждой экспертной группе проводится опрос на предмет выявления предпочтений.

Этап 2. Исследование предпочтений с целью формирования нечетких множеств. В группах «Достигатель» исследуются предпочтения в выборе типа вкладки «Достижения», для типа пользователя «Социальщик» – вкладки «Социализация», а для «Исследователя» – вкладки «Информация». Каждому из типов присваивается свое значение переменной величины X.

Эксперты в каждой из групп могут выбрать один из трех основных типов исследуемой вкладки, соответствующей Min (X=0), Middle (X=0,5), Max (X=1), либо промежуточные между этими типами значения: Min – Middle (X=0,25) либо Middle- Max (X=0,75). Статистика выбора фиксируется, и на ее основе составляются нечеткие множества предпочтений. Например, пусть в группе 1 (ярко выраженный достигатель) получено следующее распределение: тип вкладки Min выбрал 1 человек; Min – Middle – 4 человека; Middle – 5 человек; Middle- Max – 8 человек, Max – 12 человек.

На основе приведенной статистики формируются нечеткие множества AY1 («интерфейс Достижения базовый»); AY2 («интрефейс Достижения развернутый»); AY3 («интрефейс Общение психотипно-ориентированный»).

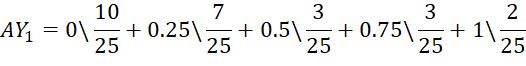
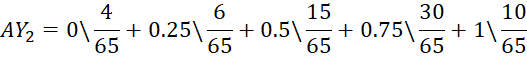
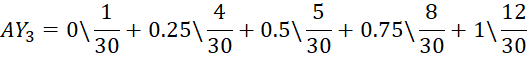
Этап 3. Формирование системы нечетко-логических выводов. В группах «Достигатель» исследуется статистика за 30 дней количества баллов, набранных при обращении к вкладке «Достижения», в среднем за месяц работы. Пусть в Группе 1: 3 человека набрали 10 баллов; 4–30 баллов; 6–50 баллов; 7–70 баллов; 10–90 баллов. На основе статистики баллов за 30 дней составлены три нечетких множества: AX₁ («уровень заинтересованности достижениями малый»), AX₂ («уровень заинтересованности достижениями средний»), AX3 («уровень заинтересованности достижениями высокий»).

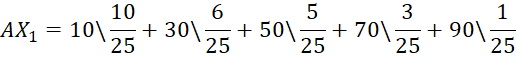
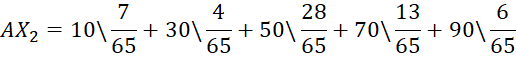
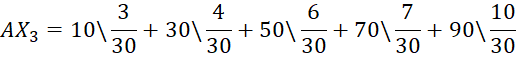
В результате формируем систему нечетко-логических выводов.

ПРАВИЛО Ach1: ЕСЛИ X2 = AX1 («уровень заинтересованности достижениями малый»), ТО Y2 = AY1 («интерфейс Достижения базовый»);

ПРАВИЛО Ach2: ЕСЛИ X2 = AX2 («уровень заинтересованности достижениями средний»), ТО Y2 = AY2 («интрефейс Достижения развернутый»);

ПРАВИЛО Ach3: ЕСЛИ X2 = AX3 («уровень заинтересованности достижениями высокий»), ТО Y3 = AY3 («интрефейс Достижения психотипно-ориентированный»).

Аналогично на основе анализа статистики в контрольных группах формируются системы нечетко-логических выводов для вкладок «Социализация» и «Информация».

Этап 4. Работа с продуктивными правилами для конкретного пользователя. Выбор типа вкладки для конкретного пользователя осуществляется на основе статистики баллов, набранных им за 30 дней.

AX – нечеткое множество, поданное на вход. Система продуктивных правил отвечает на вопросы: какую вкладку (и с какой вероятностью) он предпочел бы на основе имеющейся статистики? Ответ, рассчитанный на основе нечеткого вывода Мамдани , получаем в виде нечеткого множества:

Затем выполняем центрирование нечеткого множества:

.

На выходе как результат распознавания полученной оценки множеству получаем предпочтительный средний уровень middle.

3.3. Оценка уровня сформированности компетенции у студента на основе нечетко-множественного агрегирования результатов аттестации

В целях повышения универсальности методики, а также ее вариативности предложена ее нечетко-множественная модификация, основанная на стандартных нечетких четырехуровневых [0,1] – классификаторах [29–30] (Konysheva, Nazarov, 2011; Blyumin, Shuykova, Saraev, Cherpakov, 2002). Рассмотрим основные этапы применения системы выводов.

Этап 1. Выделение списка исследуемых компетенций. Кластеризация списка исследуемых компетенций. Описание компетенций или их кластеров в форме наблюдаемых признаков проявления.

Этап 2. Формирование банка оценочных средств, включающего стандартные оценочные средства с учетом специальности, профиля, преподаваемых предметов, традиционных методов оценки знаний студентов, а также предлагаемых модификаций.

Этап 3. Для каждого кластера компетенций (или отдельно взятой компетенции).

3.1. Определение весовых коэффициентов видов оценочных средств с точки зрения их значимости для оценки исследуемого кластера компетенций (определяется группой экспертов). Для построения весовых коэффициентов предлагается использовать группу из n экспертов. На первом этапе каждый из экспертов должен определить парные соотношения:

,

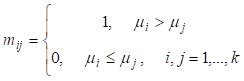где количественная оценка значимости i-го оценочного средства, k –количество используемых оценочных средств. То есть эксперт составляет матрицу, в i-й строке которой, j-м столбце стоит «1», если i-е средство оценки более значимо, чем j-е. Тогда l-я экспертная оценка весового коэффициента i-го оценочного средства вычисляется по формуле:

,

(сумму «1» в j-й строке разделить на общее количество «1» в матрице). Таким образом, некоторые оценки могут быть равны нулю. Тогда весовой коэффициент i-го показателя в группе экспертов вычисляется осреднением полученных весовых коэффициентов по группе экспертов:

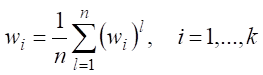. (5)

3.2. Определение весовых коэффициентов конкретных оценочных средств внутри вида с точки зрения их значимости для оценки исследуемого кластера компетенций (определяется преподавателем, осуществляющим контроль).

3.3. Расчет весовых коэффициентов для каждого конкретного оценочного средства: весовой коэффициент подгруппы*весовой коэффициент внутри группы.

Этап 4. 4.1. Формирование лингвистической переменной для оценки уровня сформированности компетенции. Вводится лингвистическая переменная: G = «уровень сформированности компетенции». Универсальным множеством для переменной G является отрезок , а множеством значений переменной – терм-множество ,

где

=«низкий уровень сформированности компетенции / неудовлетворительно»;

=«уровень сформированности компетенции ниже среднего / удовлетворительно»;

=«уровень сформированности компетенции выше среднего / хорошо»;

= «высокий уровень сформированности компетенции / отлично».

Каждый терм из множества является именем нечеткого подмножества, представляющего собой нечеткое трапециевидное число (табл. 2).

Таблица 2

Функции принадлежности подмножеств терм-множеств

4.2. Формирование лингвистической переменной для оценки выполнения вида оценочного средства. Вводится лингвистическая переменная: С_i = «оценка выполнения оценочного средства i-го вида». Универсальным множеством для переменной С_i является отрезок , а множеством значений переменной – терм-множество ,

где

С_i1 = «низкий результат выполнения / неудовлетворительно»;

С_i2 = «результат выполнения ниже среднего / удовлетворительно»;

С_i3 = «результат выполнения выше среднего / хорошо»;

С_i4 = «высокий результат выполнения / отлично».

Каждый терм из множеств С также является именем нечеткого подмножества, представляющего собой нечеткое трапециевидное число. Существенно, что изначально для оценки выполнения студентом оценочного средства задается любое удобное количество баллов (20, 40, 100 и т.д, в зависимости от существующих подходов к оценке и необходимости детализации результатов).

Этап 5. Формирование оценки уровня сформированности компетенции

Для формирования правила перехода от нормированных оценок, полученных на основе каждого средства оценки, будем использовать следующий алгоритм матричного агрегирования данных, основанного на стандартных нечетких четырехуровневых [0,1] – классификаторах [23–25] (Morcke, 2013; Jones, Voorhees, 2002; Gonzalez, 2008).

5.1. Формируем таблицу, состоящую из N строк (по количеству оценочных средств) и десяти столбцов: 1) номер оценочного средства; 2) наименование оценочного средства; 3) баллы, максимум; 4) набранные баллы; 5) нормированное значение: набранные баллы / максимум; 6) вес оценочного средства k_j, j=1,2,…N; 7–10) значения функций принадлежности термам µ_ij, i=1,2,…,5; j=1,2,…,N;

5.2. Вычисление весов термов. Согласно алгоритму стандартных нечетких четырехуровневых [0,1] – классификаторов, правило перехода от значений отдельных показателей к весам термов лингвистических переменных имеет вид:

(1)

где – значение функций принадлежности соответствующих термов, N –количество показателей в группе (здесь – количество используемых оценочных средств).

5.3. Вычисление числового значения итоговой переменной «уровень сформированности компетенции». Получим значения самой переменной g «уровень сформированности компетенции» по формуле:

, (2)

где – середина промежутка, который является носителем терма .

5.4. Лингвистическое распознавание переменной «уровень сформированности компетенции». Значение функции принадлежности будем рассматривать как меру истинности терма .

Пример практической реализации алгоритма

Этапы 1 и 2 опускаем. Этап 3.

3.1. Предположим, для оценки выбранного кластера компетенций предложены следующие 4 средства оценки: 1) контрольная работа; 2) кейс-задача; 3) расчетно-графическая работа; 4) тест.

В оценке весомости для оценки компетенций участвуют 3 эксперта.

Ими построены следующие матрицы парных соотношений:

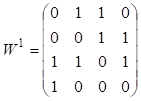
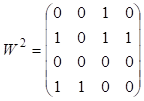
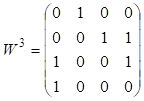
Обрабатываем результаты 1-го эксперта:

Аналогично обрабатываем результаты 2-го и 3-го эксперта.

Находим средние значения весов для каждого из средств оценки:

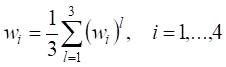
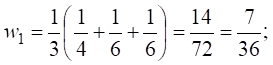
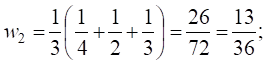
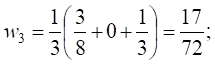
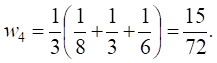
Таким образом, получены следующие весовые коэффициенты видов оценочных средств в целом: 1) контрольная работа 2) кейс-задача 3) расчетно-графическая работа 4) тест .

3.2. Будем считать, что студенту предлагаются две контрольные работы, оцениваемые по 50 баллов каждая, первая из которых считается более значимой, чем вторая (1-я – 60% материала, 2-я – 40%). Соответственно, их весовые коэффициенты будут:

Кроме того, для оценивания используются одна 40-балльная кейс-задача: и одна расчетно-графическая работа, 100 баллов: ;

Два равнозначных теста по 100 баллов каждый:

Этап 4. Будем считать, что функции принадлежностей лингвистических переменных С_i = «оценка выполнения оценочного средства i-го вида» описываются таблицей 2 (равномерное распределение).

Этап 5. 5.1.2. Составим расчетную таблицу 3 для оценки освоения студентом кластера компетенций, если он набрал:

– 1-я контрольная работа: 32 балла; 2-я контрольная работа: 44 балла;

- кейс-задача: 38 баллов;

- расчетно-графическая работа: 76 баллов;

- 1-й тест: 90 баллов; 1-й тест: 63 балла.

Таблица 3

Оценка сформированности компетенции на основе данных аттестации студента с использованием теории нечетких множеств

5.3. Центрируем полученное нечеткое множество, получаем числовое значение оценки: .

5.4. Для значения функции принадлежности термов: . Поскольку итоговое значение функции принадлежности четвертого терма значительно больше, можно утверждать, что имеет место «высокий уровень сформированности компетенции / отлично».

4. Программная реализация

Программное обеспечение разрабатывается как часть комплексной электронной информационно-обучающей среды, доступной для студентов выбранных учебных заведений. Реализован авторизованный защищенный доступ пользователей, динамическое формирование образовательного контента в соответствии с индивидуальной траекторией обучения, автоматизированный объективный контроль уровня усвоения материала, анализ и хранение достигнутых результатов.

Архитектура программной системы представляет собой клиент-серверное веб-приложение, что обеспечивает интерактивное онлайн-взаимодействие с пользователями через интернет, серверную обработку, анализ, архивирование и хранение в базе данных результатов обучения. Серверная часть системы реализована в кроссплатформенной среде ASP.NET Core на базе MS SQL Server. Клиентскую часть приложения составляет базовый контент учебника, информация в котором представлена различными мультимедийными форматами: текстовым, графическим, анимационным. Клиентская реализация, а также адаптивность для различных смарт-устройств обеспечивается применением современных технологий вэб-дизайна и разработки: HTML 5, CSS3 (в т.ч. CSS-фрэймворк bootstrap 5.0), AJAX, Java script.

Следует отметить, что оболочка интеллектуальной платформы разрабатывается независимо от ЭК и может быть наполнена любым содержанием в контексте учебных материалов. В том числе она может быть использована не только для реализации вузовских образовательных программ, но и для программ профессиональной переподготовки и повышения квалификации. Предложенный подход универсален и может быть применен к решению широкого круга образовательных задач.

Заключение

Предложена концепция интеллектуальной образовательной платформы, направленной на повышение качества образовательного процесса с использованием цифровых технологий. В основе концепции лежит комбинированное использование электронного учебника по образовательным дисциплинам, созданного на основе подхода программируемого обучения, и геймфикации, реализованной в веб-разработке оболочки указанной платформы.

Электронный учебник обеспечивает качественное изучение дисциплины в соответствии с индивидуальной траекторией обучения, а специально разработанная рейтинговая система оценки для текущего и итогового контроля обеспечивает обьективное и своевременное оценивание приобретенных знаний, умений и навыков.

Геймификация, реализованная в виде специальных вкладок, тип которых определяется на основе системы нечетких продуктивных правил, позволяет сделать максимально комфортной работу с образовательной платформой для различных психотипов учащихся, заинтересовать их, а также создать благоприятный эмоциональный фон, обеспечивающий высокие результаты в изучении дисциплин.

Методика оценки уровня сформированности компетенций у студента на основе результатов аттестации учитывает уже существующие и общепризнанные алгоритмы CBE и ее адаптации для отечественных аналогов. Она основана на агрегировании баллов, полученных при выполнении различных оценочных заданий, веса которых определяются на основе экспертных оценок. Ее преимуществом является универсальность, возможность учета любого количества оценочных средств без дополнительной подстройки расчетного алгоритма. Кроме того, она позволяет учитывать значимость различных средств оценки на основе алгоритмизированного расчета их весов с учетом мнений группы экспертов.

Методика имеет четкий алгоритм и легко реализуема на основе программного обеспечения в составе ИОП, направленной на реализацию индивидуальной образовательной траектории студента.

Предлагаемый подход обладает универсальностью и может быть использован не только для организации учебного процесса в вузе, но и в корпоративных образовательных системах, а также в разнообразных обучающих программах, рассчитанных на разноплановую неоднородную аудиторию.