Цифровая фотография как нематериальный актив в портфеле креативного инвестора

1. Введение

Исследование посвящено развитию методов инвестирования в цифровые нематериальные активы. В предыдущих работах авторов исследовались ключевые инвестиционные характеристики цифровых активов авторского права, особенности их рыночного оборота, были выстроены некоторые подходы к инвестиционному анализу портфелей активов такого класса. В частности, в сфере оборота цифровых изображений авторами были накоплены наблюдения, охватывающие более чем десятилетний период [4]. Анализ полученных экспериментальных данных позволил авторам впервые выявить эффект инерционности у активов подобного класса, а также сформулировать гипотезу импульсной структуры денежного потока совокупного дохода по портфелю цифровых изображений [5].

Понятие «креативный инвестор», вынесенное в заголовок статьи, требует дополнительного объяснения. В экономической литературе это понятие обычно связывают со способностями инвестора генерировать новые инвестиционные идеи [10]. Однако полученные авторами наблюдения позволяют утверждать, что процесс инвестирования в активы авторского права во многом связан с творческой деятельностью экономических субъектов, участвующих в этом процессе. Проведенный авторами анализ в рамках так называемого теста Хауи (Howey Test [9]) показал, что применительно к активам исследуемого класса инвесторами могут выступать:

· авторы, т.е. непосредственные создатели активов;

· компании, которые создают такие активы в процессе своей производственной деятельности, имеющей творческий характер, располагают для этого профессиональным оборудованием, технологиями, студиями, актёрским (модельным) составом;

· индивидуальные инвесторы и/или компании, приобретающие на законном основании права владения или распоряжения активами.

По версии авторов, первые две категории инвесторов могут быть названы креативными инвесторами, поскольку их права владения и распоряжения активами вытекают непосредственно из факта создания активов. Таким образом, креативность здесь имеет прямое отношение к творческому процессу создания активов авторского права.

Целью работы является развитие методов инвестирования в цифровые нематериальные активы авторского права.

Научная новизна заключается в том, что авторами впервые доказана гипотеза о пуассоновской природе потока случайных событий продажи цифровых активов исследуемого класса, и событий получения денежного дохода от их продажи.

2. Основная часть

Одной из ключевых особенностей процесса инвестирования в цифровые активы авторского права является высокая неопределенность в отношении конечной величины дохода от продажи каждого актива, имеющегося в портфеле. Рыночными посредниками в инвестиционном процессе здесь выступают компании – микрофотостоки (фотостоки), сформировавшие за последние 20 лет достаточно устойчивый оборот цифровых изображений, видео, и звуковых файлов. Достаточно отметить, что лидеры отрасли – компании Shutterstock и Adobe Stock уже вышли на фондовый рынок. Тем не менее, ни посредник, ни автор/инвестор (он же – креативный инвестор) не знает заранее, какой именно актив в портфеле будет продан, в какой момент времени состоится событие продажи, и какая именно сумма дохода при этом будет получена. Одной из причин неопределенности является широкий набор опций и тарифов, предлагаемых потребителям.

В частности, например, компания Shutterstock продает все цифровые изображения в 3-х версиях физического размера. Если обычное (т.е. не для редакционного использования) растровое изображение, размещенное автором/инвестором, имеет исходный размер около 3000 х 2000 пиксел, то компания автоматически дополняет его еще двумя версиями, имеющими размеры, соответственно, в три раза меньше (1000 х 669 пиксел), и в шесть раз меньше (500 х 335 пиксел) по каждой из сторон. Таким образом, если потребителю не требуется изображение максимального размера, то он может сразу купить более дешевую версию меньшего размера, и не преобразовывать его в дальнейшем самостоятельно, что является дополнительным удобством.

Далее пользователь должен выбрать – в какой ценовой категории продаж он будет покупать изображения:

· по подписке (Subscription);

· по запросу (On Demand);

· стандартная или расширенная лицензия (Enhanced License);

· одиночные и прочие продажи (Single and Other).

Этот выбор очень существенно влияет на стоимость каждого актива для конечного пользователя. Самой выгодной является покупка по годовой подписке. Отметим, что эта опция в настоящее время реализована на всех фотостоках без исключения, а в экономической литературе ее относят к одной из существенных финансовых инноваций. Она заключается в том, что, уплатив авансом некоторую фиксированную сумму, пользователь получает возможность покупать на выбор от 10 до 750 любых изображений (количество у разных компаний может отличаться) в месяц в зависимости от величины аванса (таблица 1). Например, при годовой подписке на Shutterstock, уплатив ежемесячный аванс 169 долл., потребитель получает возможность скопировать 350 любых изображений на выбор в течение месяца. Естественно, что такая подписка очень выгодна для тех, кому постоянно требуется большое количество новых изображений различной тематики – это графические и веб-дизайнеры, издательства, рекламные агентства и т. д.

Таблица 1

Тарифы на годовую подписку с ежемесячным авансом

Если у пользователя нет постоянной потребности в таких больших количествах изображений, то он может воспользоваться тарифами и опциями для покупки «по запросу» (таблица 2). Здесь действуют компромиссные условия для более редких покупок. Например, по стандартной лицензии Shutterstock за 229 долл. можно скопировать 25 изображений в течение года на выбор. А по лицензии с расширенными правами на использование актива за 25 изображений в год придется заплатить уже 1699 долл. аванса. Это объясняется более широкими возможностями использования таких изображений в издательском и рекламном бизнесе, в частности, более высокими тиражами продукции, в которой будут использоваться купленные изображения. Отметим, что авторы/инвесторы также получают доход от продажи своих изображений в категории «по запросу» более высокий, чем от продаж по подписке.

Таблица 2

Тарифы на покупку изображения «по запросу»

Таким образом, возможность самостоятельного выбора пользователями любых из перечисленных выше опций дает в результате самые разные комбинации сумм, получаемых фотостоком за продажу (копирование) одного и того же изображения. Кроме того, если пользователь не является постоянным подписчиком, то для него устанавливаются отдельные, более высокие тарифы в категории «единичных и прочих» продаж (Single and Other). Также имеются свои особенности ценообразования для новостных и других изображений редакционного характера (лицензия типа Editorial), и для векторных изображений. В итоге, именно широкие возможности выбора опций и тарифов объясняют диспропорции между количеством продаж конкретных активов и соответствующими доходами, получаемыми при этом как фотостоком, так и автором/инвестором.

Таковы, условно говоря, «объяснимые» причины неопределенности финансового результата инвестирования. Однако существуют другие, более глубокие причины, обусловленные творческой природой активов исследуемого класса. В частности, специалисты сходятся на том, что заранее спрогнозировать спрос на конкретный актив практически невозможно. Это приводит к тому, что существенную часть портфеля (иногда более половины) могут составлять активы, продажи которых не состоялись, и возможно, не состоятся в перспективе.

Жесткий инспекторский контроль качества, категоризация по тематике, фильтрация повторов и другие меры фотостоков не решают эту проблему, в основном лишь защищая коллекции изображений от переполнения. В связи с этим, упрощенное потребительское отношение к готовой цифровой фотографии явно требует пересмотра. Отметим, что упоминание «готовой» фотографии здесь имеет значение, т.к. исследования авторов посвящены экономическому обороту именно готовой, а не заказной фотографии. Также отметим, что исследования сущности фотографии как явления в последние годы раскрыли некоторые ее необычные аспекты, которым ранее не придавалось значения, но которые еще более усилили неопределенность ее смысла, содержания и ценности.

В частности, в ряде работ феномену фотографии противопоставляется рационализм экономических отношений, который обеспечивает непрерывный последовательный обмен товаров и денег, как в прямом, так и в обратном направлениях. Подразумевается, что при этом всегда существует возможность обмена денег на товар, и товара на деньги. Более того, показано, что то же самое наблюдается и в сфере оборота некоторых абстрактных ценностей, где, например, происходит столь же безостановочный последовательный обмен знаков (формы) на их смысловое содержание [2].

С фотографией же оказывается всё иначе, а именно, с помощью фотографии «существует возможность превратить объект в предмет изображения, но обратный обмен и обратное движение невозможны» [3, с. 112]. По этой причине фотография может не соответствовать принципам количественных эквивалентов. Изображение едва ли поддерживает математические или структурные принципы. Содержание фотографии почти всегда условно, оно редко сводится к единому резюме. Несмотря на свою, казалось бы, непосредственную связь с достоверным миром, фотография не соответствует принципам реальности предмета. Причина этого кроется в том, что сделанная однажды, фотография «… никогда не оперирует подлинными объектами» [3, с. 115].

Кроме того, немаловажная роль в фотографии принадлежит также ее технической составляющей, связанной в первую очередь с развитием оптики, а в последние десятилетия с достижениями в сфере информационных технологий. Технический аспект фотографии был отмечен еще в начале прошлого века В. Беньямином, который заметил, что «… природа, открывающаяся камере, – другая, чем та, что открывается глазу» [1, с. 105]. Таким образом, в совокупности все перечисленные выше аспекты делают готовое, в том числе цифровое изображение чрезвычайно высокорисковым активом.

Инвестиционный анализ подобных активов (портфелей) является сложной задачей. Многолетние наблюдения, накопленные авторами, позволили впервые выявить эффект инерционности инвестиционного дохода и сформулировать гипотезу об импульсной природе денежного потока, формируемого как отдельным активом, так и портфелем активов в целом [5]. В рамках выдвинутой гипотезы весь процесс продажи активов во времени рассматривается как однородный поток случайных событий, распространяющийся в направлении оси абсцисс (рис. 1). Одно событие в таком потоке соответствует одной состоявшейся продаже (т.е. продаже один раз) актива. По сути, такой поток состоит из элементарных неделимых случайных событий (1; 2; 3, … i), т.е. таких событий, дальнейшая дискретизация которых невозможна.

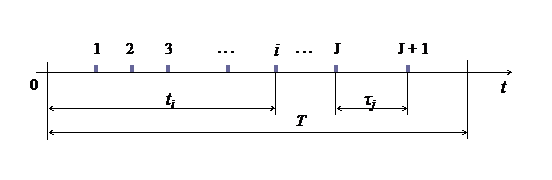
Рисунок 1. Случайный поток элементарных событий продажи индивидуального актива. (Источник: составлено авторами)

Приведём основные характеристики потока случайных событий продажи, представленного на рис. 1:

Т – время наблюдения, может варьироваться в зависимости от выбранного периода исследования;

t_i – момент совершения i-го случайного события продажи;

τ_j – интервал между событиями, является случайной величиной;

λ – интенсивность потока событий, т.е. сколько в среднем событий происходит за единицу времени.

Точные моменты времени совершения очередных событий в таком потоке неизвестны. Если известно, сколько событий n произошло за время наблюдения, то λ = n/T.

В теории вероятностей принято рассматривать подобные потоки событий в рамках модели потока бесконечно коротких импульсов, т.е. таких импульсов, продолжительность которых можно считать бесконечно малой [7]. Важнейшими наблюдаемыми характеристиками такого потока являются моменты появления случайных импульсов и интервалы между ними, которые также являются случайными величинами. Кроме того, отметим, что импульсы в некоторых процессах могут иметь и разную амплитуду.

Поток бесконечно коротких импульсов в общем случае называется пуассоновским, если он удовлетворяет требованиям ординарности и отсутствия последействия. Кроме того, поток может быть стационарным или нестационарным, т.е. таким потоком, у которого интенсивность, в свою очередь, зависит от времени.

Поскольку в нашем случае вероятность наступления событий продажи активов не зависит от моментов предыдущих продаж, а вероятность одновременной продажи двух и более активов можно считать близкой к нулю, то поток случайных событий продажи активов можно считать пуассоновским потоком (потоком редких событий). Амплитуда всех импульсов потока событий продаж является одинаковой, для удобства будем считать ее равной единице.

Вероятность того, что за время наблюдения произойдет n событий в пуассоновском потоке, равна:

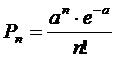, (1)

где – параметр Пуассона, который для стационарного потока равен среднему числу событий за время наблюдения. Как известно, математическое ожидание, как и стандартное отклонение значений интервалов между событиями у такого потока равны величине, обратной интенсивности потока [6]. С одной стороны, это говорит о том, что рассеяние значений времени наступления событий в потоке редких событий велико и плохо предсказуемо. С другой стороны, это дает возможность проверить гипотезу о пуассоновском распределении событий исследуемого потока. В частности, если найденные экспериментальным путем значения матожидания и стандартного отклонения окажутся близкими, то это может служить эмпирическим доказательством в пользу гипотезы о пуассоновском распределении.

На рис. 2 показано посуточное распределение случайных импульсов потока событий продажи изображения SN в августе 2013 г., полученное авторами в результате наблюдений. Данное изображение взято из реального исследуемого портфеля, размещенного на Shutterstock. Как было отмечено выше, амплитуда всех импульсов событий продажи одинакова, поскольку один элементарный импульс отображает одно событие продажи.

Рисунок 2. Распределение случайных импульсов потока событий продажи изображения SN в августе 2013 г. (Источник: составлено авторами)

Накопление или увеличение частоты случайных событий продажи позволяет объединять импульсы в группы, соответствующие суточным, квартальным, годовым и другим периодам наблюдения. В таких группах общее количество событий можно рассматривать как суммарные амплитуды импульсов продажи. Характеристиками таких суммарных импульсов уже являются соответствующие огибающие кривые, позволяющие переходить к анализу более сложных непрерывных случайных процессов.

Например, совокупность накопленных торговых событий, отображающая полный исторический ряд случайных событий продажи изображения SN за 2011-2019 гг. показана на рис. 3. За указанный период времени изображение SN было продано (скопировано) всего 254 раза. Диаграмма построена таким образом, что каждый ее стержень отображает сумму всех элементарных событий продажи данного актива за соответствующий год, указанный на оси абсцисс.

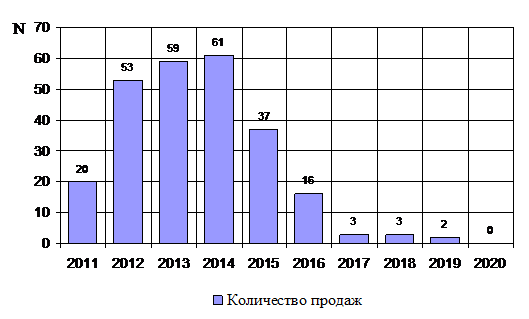
Рисунок 3. Количество событий продажи изображения SN за 2011-2019 гг., во всех категориях. (Источник: составлено авторами)

В отличие от диаграммы потока элементарных случайных событий (рис. 2) годовая диаграмма на рис. 3 отображает более сложный случайный процесс, в котором становится возможным выделение фронта нарастания (2011-2012 гг.), затем продолжения (2012-2014 гг.) и спада (2014-2019 гг.) информационного параметра суммарного импульса количества продаж данного актива. Кроме того, можно выделить характерный участок диаграммы (2016-2019 гг.), который по сравнению с устойчивым потоком 2012-2014 гг. представляет так называемый редеющий (разреженный) поток случайных событий, интенсивность которого в десятки раз ниже. Анализ таких потоков до настоящего времени представляет серьезную математическую проблему [8].

Визуальный анализ диаграммы говорит о том, что поток случайных событий продажи активов предпочтительно рассматривать как стационарный только в годовых периодах. Соответственно, количество событий продаж в каждом годовом периоде можно использовать для оценки интенсивности потока и вероятностных параметров.

Наличие полного ряда исторических данных позволило авторам впервые проверить гипотезу о пуассоновском распределении случайных событий продажи активов исследуемого класса. С этой целью стандартными средствами статистического анализа были найдены параметры матожидания и стандартного отклонения значений интервалов между элементарными событиями потоков продаж исследуемых активов. В частности, по изображению SN за период 2013-2014 гг. (в сумме 120 событий продаж) были получены:

- матожидание μ = 6,19 суток;

- стандартное отклонение σ = 6,06 суток.

Разница между полученными значениями составляет менее 3%, что подтверждает гипотезу авторов о пуассоновском распределении случайных событий в исследуемых потоках. Подтверждение пуассоновской природы потока дает возможность делать вполне обоснованные оценки вероятностей ненаступления событий продажи (Р₀) и наступления хотя бы одного события (Р_ХБ1). В частности, из выражения (1) при полном отсутствии наблюдаемых событий (n = 0) получаем:

. (2)

В свою очередь, вероятность наступления хотя бы одного события определяется как противоположное событие:

. (3)

Выражения (2) и (3) имеют большое практическое значение, т.к. они дают возможность оценить риск полного прекращения продажи актива, и наоборот, оценить вероятность реализации как минимум одного торгового события при существующих (наблюдаемых) параметрах случайного потока торговых событий конкретных активов. Например, в таблице 3 приведены значения вероятности полного прекращения продажи и вероятности как минимум одной продажи изображения SN в среднем за месяц, для которого все параметры потока случайных событий известны. Данные таблицы 3 говорят о том, что, начиная с 2016 г. вероятность полного прекращения продажи данного изображения увеличивается до 26%, затем поток торговых событий редеет, и к 2020 г. продажи прекращаются полностью. Подобные оценки очень важны для построения логико-вероятностных моделей поддержки принятия решений инвестора.

Таблица 3

Вероятности прекращения продажи и наступления как минимум одного события продажи изображения SN в среднем за месяц

Вторым информационным параметром исследуемого процесса является доход от продажи актива (выручка). В соответствии с гипотезой авторов об импульсной структуре денежного потока, второй поток случайных событий получения дохода отличается тем, что каждое событие потока имеет дополнительную характеристику – амплитуду (рис. 4). Это объясняется тем, что каждое случайное неделимое событие получения дохода представляет конкретную денежную сумму, полученную в результате торгового события. На оси ординат в этом случае откладывается величина дохода в денежном выражении, а диаграмма представляет поток случайных импульсов.

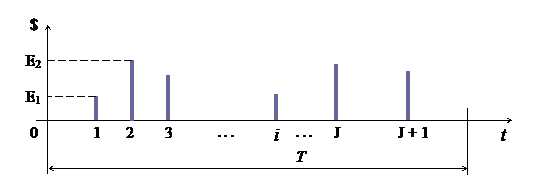
Рисунок 4. Случайный импульсный поток элементарных событий получения дохода от продажи индивидуального актива. (Источник: составлено авторами)

В частности, диаграмма на рис. 4 построена таким образом, что все элементарные импульсы дохода точно соответствуют по времени торговым событиям диаграммы рис. 2, но при этом амплитуды всех импульсов дохода различны (например, амплитуда Е₂ > Е₁), т.к. они отображают доход в денежном выражении.

На рис. 5 показано распределение случайных импульсов потока дохода от продажи изображения SN в августе 2013 г., построенное по результатам наблюдений. Данная диаграмма синхронна по времени с диаграммой событий продаж, представленной выше на рис. 2, но все импульсы потока имеют амплитуду, отображаемую в денежном выражении на оси ординат.

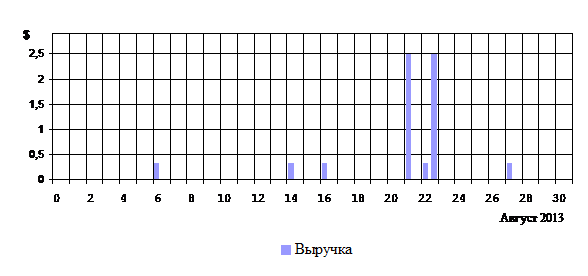
Рисунок 5. Распределение случайных импульсов потока дохода от продажи изображения SN в августе 2013 г. (Источник: составлено авторами)

Так же, как в случае элементарных торговых событий, накопление или увеличение частоты поступления элементарных импульсов дохода позволяет объединять их в группы, соответствующие суточным, недельным, квартальным, годовым и другим периодам, и таким образом переходить к непрерывным случайным процессам, характеристикой которых является огибающая кривая. Например, на рис. 6 приведена диаграмма, отображающая полную совокупность элементарных импульсов дохода от продажи изображения SN за 2011-2019 гг. Каждый стержень диаграммы отображает сумму элементарных импульсов дохода за соответствующий год, указанный на оси абсцисс. Анализ данной диаграммы показывает, что она не является масштабированной копией синхронной по времени диаграммы событий продаж, приведенной на рис. 3. Отсутствие пропорциональности диаграмм между собой подтверждается также и значением коэффициента корреляции между массивами данных о продажах и выручке, равным 0,966.

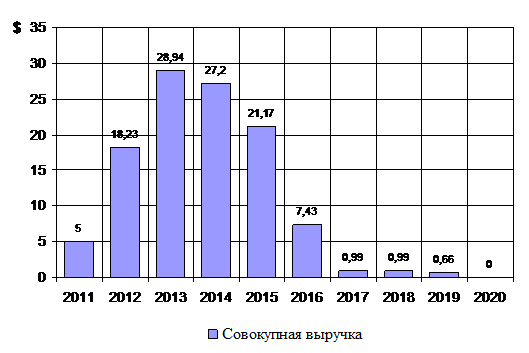
Рисунок 6. Совокупный доход от продажи изображения SN за 2011-2019 гг. (Источник: составлено авторами)

На диаграмме рис. 6 можно выделить начальный фронт, нарастающий около двух лет (2011-2012 гг.); затем – период стабилизации около некоторого максимального значения (2013-2014 гг.); затем – спад до полного прекращения дохода (2015-2019 гг.). В одной из предыдущих работ авторов было показано, как с помощью диаграммы подобного типа можно количественно определить амплитуду, длительность фронта, длительность импульса в целом, и длительность спада, т.е. количественно описать все основные параметры такого импульса [5]. В соответствии с предложенной концепцией полный денежный поток инвестиционного дохода по портфелю формируется завершенными и текущими (незавершенными) импульсами отдельных активов. По версии авторов инерционные свойства портфелей подобного типа объясняются тем, что в любой фиксированный момент времени портфель генерирует множество случайных незавершенных импульсов дохода. Именно перекрытие во времени взаимно независимых импульсов дохода обеспечивает длительное непрерывное поступление инвестиционного дохода.

3. Заключение

Появление новых рыночных институтов, подобных микрофотостокам позволило массовой, особенно молодежной аудитории использовать в качестве инструмента инвестиций интеллектуальную собственность, которая сегодня имеется в избытке буквально в любом смартфоне. Оптика и микроэлектроника достигли такого уровня, что цифровые фотографии, полученные с помощью камеры современного смартфона, при наличии определенных навыков и креативных способностей пользователя превращаются в инвестиционный ресурс, которого не существовало в принципе всего 5-7 лет назад. Более того, появились новые фотостоки (например – EyeEm), полностью ориентированные на фотографии, полученные с помощью мобильных устройств.

Тем не менее, проблемы, связанные с инвестированием в интеллектуальные активы, в том числе в цифровые активы исследуемого класса, с наступлением «цифровой эры» не уменьшились. Инвесторы по-прежнему (и вполне справедливо) считают любую интеллектуальную собственность источником избыточных рисков и неопределенностей.

В представленной работе впервые доказано, что поток случайных событий продажи цифровых изображений в портфеле автора/инвестора подчиняется закону Пуассона. В свою очередь, это дает в руки инвестору достаточно простые средства для количественной оценки вероятности полного прекращения продаж, как по отдельным активам, так и по портфелю в целом. Кроме того, гипотеза об импульсной структуре денежного потока, выдвинутая авторами, вносит вклад в общее понимание процесса формирования совокупного инвестиционного дохода по портфелю.

Как было отмечено, ведущие фотостоки уже вышли на фондовый рынок и стали публичными компаниями. Поэтому сегодня не только креативный (автор/инвестор), но любой инвестор может приобрести акции фотостока и стать опосредованным участником рынка интеллектуальной собственности. Однако креативный инвестор, покупая такие акции, получает возможность участия в распределении прибыли самого фотостока, и становится своего рода гибридным инвестором, получающим дополнительный дивидендный доход. Аспекты подобного гибридного инвестирования ранее не исследовались, и являются перспективой научной задачей.