Выбор модели оценки текучести персонала

Введение

Текучесть кадров определяет сотрудников, которые покинули фирму и были заменены новыми в течение финансового года. Каждое коммерческое предприятие осознает тот факт, что поддерживать существующий штат сотрудников дешевле и эффективнее, чем нанимать новых. Уволен работник или ушел по собственному желанию, в конце концов, не имеет значения, потому что в обоих случаях компания должна заново настраивать процесс найма, а это означает дополнительные расходы. Текучесть кадров оказывает прямое влияние на размер прибыли, поскольку в промежуточный период фирма теряет доход и производительность [1, 2] (Kibanov, Durakova, 2020).

Однако в текучести кадров есть и положительные моменты. В постоянно меняющемся мире появляются новые и передовые технологии. Это ставит новые задачи и возможности для их успешного решения: фирме нужен персонал, способный эффективно с ними справляться. Персонал, который работает в компании долгое время и не пользуется новыми программами обучения, не сможет успешно понять и справиться с изменениями. Для фирмы будет лучше, если они уйдут добровольно или недобровольно, поскольку в обоих случаях их можно заменить новыми сотрудниками, обладающими необходимыми знаниями для развития фирмы. Текучесть кадров в таких случаях улучшит текущие таланты, успешно интегрировавшись с ними.

В ситуации найма новых сотрудников и увольнения старых в компанию привносится волна свежих взглядов и новых идей, а также инновационные идеи. Большему количеству бывших сотрудников приходится сталкиваться с жесткой конкуренцией со стороны новой партии, и эта здоровая конкуренция оказывается выгодной для предприятия.

Наряду с преимуществами в текучести кадров имеются и недостатки, в частности: такой процесс в конечном итоге стоит денег, времени и усилий, что означает растрату ресурсов; приводит к новым программам обучения для новых сотрудников, что также создает дополнительные расходы; увольнение работников отрицательно сказывается на моральном духе других сотрудников фирмы, и это снижает производительность труда; компании с высокой текучестью кадров с трудом выполняют свои обязательства и укладываются в установленные сроки различных проектов.

В различных источниках, например [3, 4] (Tselyutina, Litvin, 2019), определяются нормативы текучести, чаще всего равные отношению числа уволившихся за фиксированный период времени (обычно год) к среднесписочному составу организации. Приемлемая норма текучести около 3–5% свидетельствует о нормальном обновлении персонала. Меньшие значения показателя характеризуют застойные явления в компании; значения, превышающие 50%, приводят к заключению о серьезных проблемах в работе с персоналом.

Важным для любой организации является вопрос прогнозирования такого явления, как текучесть. Во многих компаниях проблемы с текучестью диагностируются в тот момент, когда уже сложно на что-то повлиять. Зачастую даже в тех ситуациях, когда текучести персонала уделяют достаточно внимания, многие факторы не учитываются, что не позволяет вовремя и точечно определить узкие места в процессах управления персоналом.

В случае текучести кадров использование предиктивной аналитики считается не только выгодным для людей, но и экономит финансы компании: когда квалифицированный член команды уходит по собственному желанию, это всегда связано с большими затратами времени и денег на поиск и адаптацию подходящей замены. Кроме того, это может повлиять на общую производительность фирмы, лояльность клиентов и своевременную доставку продукции. Несмотря на то, что попытки предсказать текучесть кадров с помощью современной аналитики кажутся имеющими огромный потенциал, существует ряд ограничений, которые могут затруднить перенос этих научных результатов на реальные примеры из отрасли.

При работе с данными можно использовать любую из следующих стратегий: если нашей целью является прогнозирование соответствующих результатов, нам не нужно полностью понимать задействованные механизмы [5] (Yarkoni, Westfall, 2017). Наша стратегия будет скорее ориентирована на прогнозирование. В случае с проблемой текучести кадров мы, возможно, не хотим терять слишком много времени, ломая голову над «почему», когда мы уже можем спрогнозировать, какие сотрудники рискуют скоро уйти – в конце концов, наш шанс что-то изменить лежит только в будущем.

Результаты прогнозирования текучести кадров часто бывают неоднозначными, специфичными для конкретной проблемы и трудно поддаются обобщению. Это объясняется тем, что данные кадровых служб являются конфиденциальными, а это, в свою очередь, препятствует проведению углубленного анализа различных наборов данных.

С помощью методов машинного обучения исторические и размеченные данные о сотрудниках можно использовать для выявления характеристик, которые могут быть связаны с высокой производительностью труда, чтобы впоследствии предсказать вероятность того, что новый сотрудник будет хорошо выполнять свою работу [6]. Следовательно, данные о производительности других людей вместе с некоторыми ключевыми показателями (например, IQ, личностные тесты, результаты структурированных интервью) или их биографические данные служат основой для прогнозирования производительности нового сотрудника. Вследствие этого алгоритм обучается на данных из прошлого, чтобы предсказывать будущее.

В отношении инструментария для оценки текучести персонала можно указать ряд работ, в которых описано применение различных методов машинного обучения [7–11] (Alao, Adeyemo, 2013; Punnoose, Ajit, 2016). Очевидно, что указанный перечень не полон, поэтому появление еще одной публикации в этой области может быть оправдано использованием единой методологии и программного продукта (MatLab 2020). В последнем такого рода задачи решаются с формированием итоговой оценки точности классификации, и уже не требуется сравнивать площади под кривыми операционных характеристик различных методов, просматривать матрицы ошибок.

Цель работы состоит в представлении и демонстрации пяти приемов машинного обучения, включающих дискриминантный анализ, решающие деревья, случайный лес, методы ближних соседей и опорных векторов для прогнозирования текучести сотрудников в организации.

Методология

1. Машинное обучение

Под термином «машинное обучение» понимается технология, которая в [12] (Alpaydin, 2010) определена следующим образом: «Оптимизация критерия производительности модели с использованием данных и прошлого опыта». У нас есть модель, определенная с точностью до некоторых параметров, а обучение – это выполнение компьютерной программы для оптимизации параметров модели. Указанный термин относится к автоматическому обнаружению значимых закономерностей в данных. За последние 20 лет машинное обучение стало обычным инструментом в любой задаче, требующей извлечения информации из наборов данных. Мы находимся в окружении технологий, основанных на машинном обучении: программы для защиты от спама учатся фильтровать сообщения электронной почты, транзакции по кредитным картам защищены программным обеспечением, которое учится обнаруживать мошенничество, автомобили оборудованы системами предотвращения аварий, созданных с использованием таких алгоритмов.

Только за последние два десятилетия была признана присущая машинному обучению междисциплинарность [13] (Marsland, 2015). Этот вид обучения объединяет идеи нейробиологии, статистики, математики и физики для того, чтобы компьютеры обучались. Еще одна вещь, которая привела к изменению направления исследования машинного обучения, – это интеллектуальный анализ данных, который направлен на извлечение полезной информации из массивных наборов данных и требует эффективных алгоритмов, делающих больший акцент на информатике.

В алгоритмах машинного обучения при решении задачи текучести процесс состоит из двух фаз: обучения и использования (прогнозирования) (рис. 1).

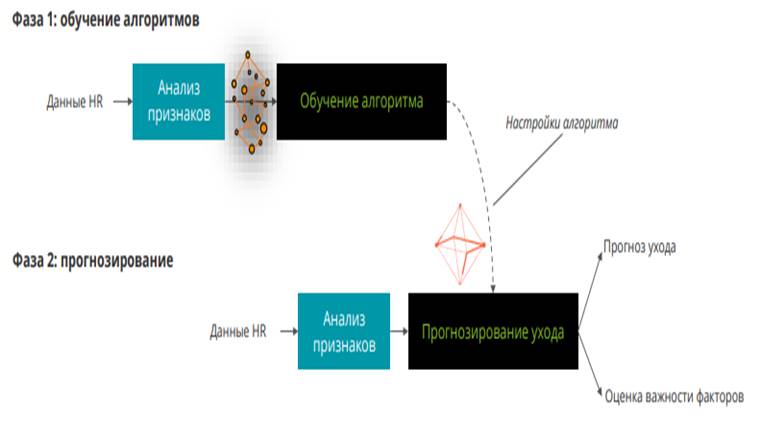
Рисунок 1. Алгоритм машинного обучения

Источник: [14].

На первом этапе алгоритм обучается, а на втором – используется по назначению.

2. Методы классификации

Машинное обучение по базе примеров формирует модель, которая в дальнейшем может быть использована для других задач, например прогнозирования. В ряде работ датасетом для проведения оценок текучести служит смоделированный набор данных, созданный IBM Watson Analytics, который можно найти на Kaggle. Эта база данных содержит 1470 записей о сотрудниках и 38 общих характеристик (ежемесячный доход, удовлетворенность работой, пол и т. д.) и целевую переменную: увольнение (да/нет) [9]. Однако, по мнению авторов, такой большой объем данных может скрыть истинные факторы, приведшие сотрудника к принятию решения об увольнении. По этой причине в работе рассматривается также смоделированный набор данных ("toy dataset"), поскольку в машинном обучении важно научиться правильно применять игрушечные наборы данных, так как обучение алгоритма на реальных данных сопряжено с трудностями и может закончиться неудачей [15] (Ramsundar, Zade, 2019). Разыгранные наборы данных играют решающую роль для понимания работы алгоритмов. При наличии простой синтетической выборки данных достаточно просто оценить, обучился алгоритм нужному правилу или нет. На реальных данных получить такую оценку сложно.

2.1. Формирование данных

Отобранными переменными были выбраны такие признаки работников: Х1 – удовлетворенность работой; Х2 – возраст; Х3 – зарплата; Х4 – время, затрачиваемое на дорогу до работы; Х5 – климат в коллективе; Х6 – количество лет, проведенных в компании; Х7 – время работы с одинаковым окладом; Х8 – должность (позиция). Переменные Х2, Х3, Х4, Х6, Х7 определялись как числовые величины, разыгранные в выбранном диапазоне их изменений. Остальные признаки рассматривались как оцениваемые по балльной шкале в диапазоне от 1 до 10 баллов. Выходной переменной являлась дихотомическая величина, которая характеризовала поведение работника: остается или увольняется. Смоделированная матрица состояла из 40 строк (работников) и 10 столбцов (9 признаков и метка класса).

Термин «проклятие размерности» (curse of dimensionality) обычно относится к трудностям, связанным с подгонкой моделей, оценкой ее параметров или оптимизацией многомерной функции при наличии большой выборки. При увеличении размерности пространства входных данных становится сложнее найти глобальные оптимумы для этого пространства. Следовательно, актуальна практическая необходимость отбора из большого набора входных переменных тех, которые наиболее полезны для прогнозирования выходов зависимых выходных переменных.

2.2. Дерево решений

Деревья решений могут применяться как к задачам регрессии, так и классификации. Такой прием определяет метод контролируемого обучения, который строит модели классификации в виде древовидной структуры. Дерево классификации используется для прогнозирования качественного ответа, а не количественного. Для дерева классификации мы предсказываем, что каждое наблюдение относится к наиболее часто встречающемуся классу обучения наблюдения в области, к которой оно принадлежит.

Методы на основе дерева просты и удобны для интерпретации. Однако, как правило, они не могут конкурировать с лучшими подходами к обучению с учителем с точки зрения точности прогнозирования [16] (Gareth, Witten, Hastie, 2013).

Этот метод обладает следующими преимуществами:

· Некоторые исследователи считают, что деревья решений более точно отражают человеческие подходы к принятию решений.

· Деревья могут отображаться графически и легко интерпретируются даже неспециалистами.

· Деревья могут легко обрабатывать качественные предикторы без необходимости создания фиктивных переменных.

Однако деревья могут быть очень непрочными, т.е. небольшое изменение данных может привести к большим изменениям в окончательной оценке дерева.

2.3. Линейный дискриминантный анализ

Линейный дискриминантный анализ (ЛДА) – широко используемый метод математического моделирования, представляющий собой обобщение линейного дискриминанта Фишера, предложенное им еще в 1936 г. Однако несмотря на долгую историю развития этих методов, эти модели продолжают активно использоваться и сегодня в различных сферах деятельности [17] (Ezghazi, Zahi, Zekoua, 2017). ЛДА определяет оптимальную линейную комбинацию, которая может разделить данные на разные кластеры путем проецирования выборок данных в пространство более низкого размерения. В отличие от принципа главных компонент, ЛДА – метод контролируемого обучения, хотя его производительность в некоторых случаях может уступать методу главных компонент.

ЛДА предполагает, что данные нормально распределены, классы имеют идентичные ковариации, признаки независимы и одинаково распределены. Для проведения классификации ЛДА измеряет расстояние между прогнозируемыми средними значениями и использует матрицу рассеяния, чтобы максимизировать отношение расстояния выборки между классами к расстоянию выборки внутри класса.

2.4. Метод k-ближайших соседей

Классификация этим методом определяет алгоритм МО, который формирует группу из k объектов в обучающей выборке, находящуюся ближе всего к тестовому объекту. Метод k-ближайших соседей является непараметрическим алгоритмом, используемым для задачи классификации. В этой задаче идея состоит в том, чтобы идентифицировать k точек данных в обучающей выборке, которые ближе всего к новому экземпляру, и классифицировать новый экземпляр по большинству голосов своих k соседей. На практике популярные меры расстояния включают такие меры расстояний, как евклидово, манхэттенское, Минковского.

Как только появляются новые данные, работа алгоритма определяется следующей последовательностью шагов:

· находятся k ближайших соседей;

· с использованием классов соседей алгоритм решает, как лучше классифицировать новые данные.

2.5. Случайные леса

Случайные леса используют ансамблевый подход, который обеспечивает улучшение по сравнению с базовой структурой дерева решений путем объединения группы слабых учеников для формирования более сильного ученика [18] (Breiman, 2001). Методы ансамбля используют подход «разделяй и властвуй» для повышения производительности алгоритма.

По существу, случайный лес – это множество решающих деревьев. В задаче классификации решение принимается голосованием по большинству. Все деревья строятся независимо по следующей схеме:

· выбирается подвыборка обучающей выборки (может быть, с возвращением) – по ней строится дерево (для каждого дерева – своя подвыборка);

· для построения каждого расщепления в дереве просматривается набор случайных признаков (для каждого нового расщепления – свои случайные признаки);

· выбираются наилучший признак и расщепление по нему (по заранее заданному критерию). Дерево строится, как правило, до исчерпания выборки (пока в листьях не останутся представители только одного класса).

2.6. Метод опорных векторов

Метод опорных векторов (МОВ) был предложен Вапником [19] (Vapnik, 1998). Этот метод обычно используется в качестве дискриминационного классификатора для присвоения новых данных одному из двух возможных категорий. Основная идея МОВ состоит в том, чтобы определить гиперплоскость, которая разделяет n-мерные данные на два класса. Эта гиперплоскость максимизирует геометрическое расстояние до ближайших точек данных, называемых опорными векторами.

Вдобавок к выполнению линейной классификации МОВ также вводит идею использования ядерного метода для эффективного выполнения нелинейной классификации. По существу, такой прием формирует для отображения признаков методологию, которая переводит атрибуты в новое пространство признаков (обычно более высокой размерности), где данные являются разделимыми.

Результаты

Фрагмент разыгранных данных для решения задачи показан в таблице 1.

Таблица 1

Фрагмент смоделированных данных

Источник: составлено авторами.

Напомним, что вся матрица данных содержит 40 строк. Далее перейдем к формированию сокращенного набора признаков. Методы, которые реализованы в модуле Feature Selection программы Statistica, предназначены для обработки больших наборов непрерывных и/или категориальных предикторов в задачах типа регрессии или классификации. Здесь можно выбрать подмножество предикторов из большого списка кандидатов без допущения о степени отношений между предикторами и зависимыми переменными. Этот модуль может служить идеальным препроцессором в МО, позволяя выбирать сокращенные наборы предикторов для дальнейшего анализа.

С помощью этого приема проведем оценку значимости признаков. Результаты такого ранжирования приведены на рисунке 2.

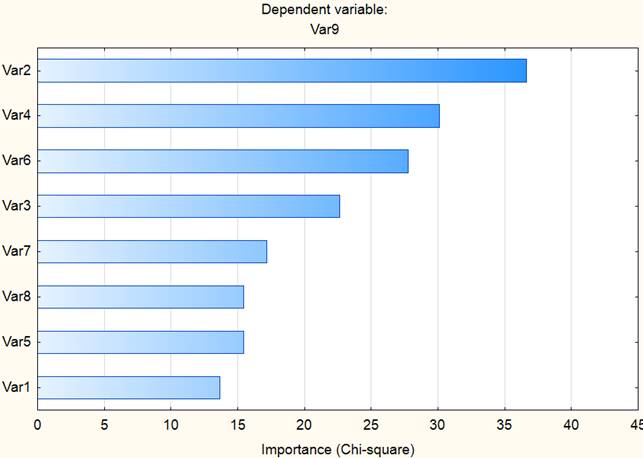
Рисунок 2. График важности признаков

Источник: составлено авторами.

Отберем для анализа следующие 5 переменных: Var2 – возраст; Var4 – время до работы; Var6 – количество лет в компании; Var3-зарплата; Var7 – время без повышения оклада.

Далее все расчеты проводим в MatLab. На рисунке 3 приведены итоговые результаты классификации, в которой были использованы перечисленные выше методы.

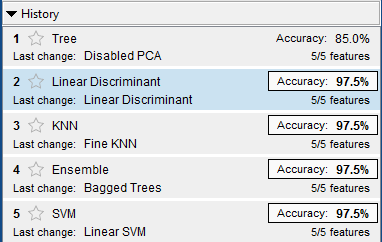
Рисунок 3. Результаты классификации

Источник: составлено авторами.

Как видно из рисунка 3, четыре метода из пяти дали одинаковые результаты точности классификации. Для дальнейшего расчета выберем метод ЛДА. Не приводя данных по матрице ошибок и операционной характеристике, перейдем сразу к оценке текучести. Для этого сохраним выбранную модель в рабочем пространстве MatLab и сформируем 5-мерный вектор оцениваемого работника, например X1 = [58.7; 1.1; 7.7; 72.2; 20.4].

Полученный для этого работника результат показан ниже:

yfit = trainedModel.predictFcn(X1)

yfit =1.

Таким образом, этот работник, скорее всего, останется в этой компании, так как выбранная модель отнесла его к классу 1 (остающихся в компании).

Обсуждение

Результаты исследования получены на смоделированных данных, и в дальнейшем целесообразно при решении задачи использовать реальные данные, однако в нахождении таких данных могут возникнуть проблемы, связанные с конфиденциальностью работы кадровых служб. Кроме того, нужно провести анализ признаков, влияющих на принятие решений. Необходим последующий анализ для определения справедливости полученных выводов. Также рекомендуется расширить это исследование, включив в него больше исходных данных и моделей.

Заключение

Таким образом, в работе продемонстрировано применение методов машинного обучения с использованием программного продукта MatLab для решения задачи по текучести персонала. Показана принципиальная возможность использования такого подхода в реальных ситуациях. Машинное обучение является составным элементом искусственного интеллекта, поэтому примененный в работе подход может служить начальным элементом при переходе к цифровой экономике. Различные задачи из области менеджмента и экономики могут быть решены аналогичным образом.