Оценка кредитного дефолтного свопа для российских коммерческих банков

Введение

В предыдущей статье «О применимости CDS для оценки кредитоспособности финансовых институтов РФ» были рассмотрены основные теоретические аспекты функционирования CDS, особенности российского рынка CDS и представлены преимущества использования спредов CDS для оценки кредитоспособности финансовых институтов по сравнению с существующими рейтинговыми моделями (Агеев, 2015).

Было показано, что присваиваемые международными рейтинговыми агентствами рейтинги обладают существенными недостатками, так как между процессом анализа финансовых данных и моментом присвоения рейтинга существует определенный временной лаг. К тому же рейтинги присвоены меньшей части существующих банков.

Одним из способов устранения этих недостатков может быть использование такого производного финансового инструмента, как CDS. Основное преимущество CDS заключается в том, что его постоянно оценивают участники рынка, которые учитывают не только данные отчетности банков, их кредитные рейтинги и другие фундаментальные оценки, но и всю доступную информацию фактически в режиме реального времени.

Современные модели оценки рисков могут основываться не только на использовании информации о тех CDS, которые торгуются на рынке, но и на построении теоретических значений CDS для контрагентов, в случае если такие инструменты на данный момент на рынке не представлены.

Проблема оценки CDS и использования полученных результатов в моделях оценки контрагентов в настоящее время еще до конца не разрешена, нет единого подхода либо устоявшихся моделей оценки, и вопрос использования того или иного инструментария для оценки CDS остается открытым.

В настоящей статье проводится практическое исследование с целью построения модели, предсказывающей теоретическое значение спредов CDS для финансовых институтов. Модель оценки CDS строится на базе данных из финансовой отчетности и каждодневного изменения существующих спредов CDS.

Статья построена следующим образом: в первой части приводятся теоретические аспекты исследования, во второй части производится обоснование используемой выборки для анализа и отбор показателей для модели, третья часть представляет собой построение модели и интерпретацию полученных выводов, заключительная часть состоит из практической проверки модели и выводов по итогам проведенного исследования.

Теоретическое обоснование модели

Существует несколько видов моделей оценки теоретического значения спреда CDS. В основном их можно разделить на два типа. Модели первого типа опираются на показатели других рыночных инструментов компании, на долг которой строится теоретическое значение спреда CDS (редуцированные модели). Модели второго типа основаны на фундаментальных показателях анализируемой компании (структурированные модели). В настоящей статье будет рассмотрена модель, основанная на фундаментальных данных.

В настоящем исследовании сделано следующее предположение: спред CDS на конкретный банк из определенной страны представляет собой спред CDS на эту страну (если быть точным, то на ее долг) плюс некоторая дельта, выражающаяся в определенных особенностях конкретного банка. Таким образом, основная задача исследуемой модели заключается в объяснении данной дельты.

В настоящем исследовании была предпринята попытка объяснить разницу между суверенным спредом и спредом на конкретный банк с помощью фундаментальных показателей финансовой отчетности.

Как было отмечено в предыдущей статье, на рынке CDS к настоящему моменту представлены восемь российских финансовых институтов: АО «АЛЬФА-БАНК», Банк ВТБ (ПАО), ОАО «Банк Москвы», АО «Банк Русский Стандарт», Внешэкономбанк, «Газпромбанк» (АО), АО «Россельхозбанк» и ПАО «Сбербанк». Проведенный анализ корреляции спредов 5-летних CDS этих банков со спредами 5-летних CDS на российский долг позволяет сделать вывод о том, что приведенное выше предположение о высокой зависимости спреда CDS на конкретный банк от спреда CDS на долг той страны, которую он представляет, подтверждается на практике (см. таблицу 1).

Таким образом, основной задачей на данном этапе исследования является отбор показателей для построения модели, которая смогла бы с достаточно высокой точностью объяснить спреды существующих CDS, что позволит в дальнейшем предсказать теоретические спреды CDS на банки, чьи CDS на рынке не торгуются.

Таблица 1

Коэффициенты корреляции между спредами 5-летних CDS на российский суверенный долг и спредами на российские банки

Формирование выборки и отбор показателей для проведения исследования

Для построения теоретических значений CDS необходимо использовать исторические данные по CDS, которые на регулярной основе котируются на бирже. Так как в России нет достаточного для проведения исследования количества банков, появилась необходимость прибегнуть к банкам в некоторых других относительно сопоставимых странах. В качестве таких стран было выбрано устоявшееся и часто анализируемое во многих работах объединение наиболее перспективных растущих экономик стран БРИКС (Бразилия, Россия, Индия, Китай и ЮАР). Данные страны имеют много общего в экономическом развитии и позициях на международных рынках. Таким образом, для цели построения теоретических значений CDS были отобраны банки из развивающихся стран группы БРИКС, CDS на долговые инструменты которых котируются на рынке.

В качестве временного периода выбран отрезок времени с начала 2011 года по февраль 2015 года. Выбор 2011 года в качестве начального периода для исследования объясняется, во-первых, желанием избежать влияния кризисных явлений на проводимое исследование, а во-вторых, тем, что наиболее качественные и заслуживающие доверия данные по котировкам спредов CDS появились в 2011 году.

Итоговая выборка банков с распределением по странам представлена в таблице 2 [1].

Таблица 2

Выборка банков из стран БРИКС для эмпирического исследования [2]

В качестве зависимой переменной выступает оцениваемое значение спреда CDS по банкам из группы стран БРИКС. Для анализа был выбран наиболее популярный и, следовательно, ликвидный по сроку вид CDS: пятилетний.

Из большого перечня потенциальных переменных были отобраны не коррелирующие между собой (приемлемый уровень корреляции 0,5). После исключения сильно взаимосвязанных переменных был сформирован следующий перечень переменных:

– «Суверенный спред CDS» (так же, как для CDS банков, для суверенных CDS был взят тот же пятилетний временной период; для Бразилии, России и Китая в качестве суверенного CDS был взят CDS на государственный долг; для Индии, так как CDS на государственный долг на рынке не представлен, был взят CDS на долг Export-Import Bank of India – этот государственный банк имеет самую низкую оценку среди индийских эмитентов);

– «Итого активы»;

– «Основные фонды / Итого обязательства»;

– «Чистая процентная маржа» (соотношение процентного дохода и суммы приносящих доход активов);

– «Средняя рентабельность активов»;

– «Коэффициент Затраты / Расходы» (соотношение административных расходов и операционной прибыли);

– «Кредиты за вычетом резервов / Итого активы»;

– «Кредиты за вычетом резервов / Депозиты и краткосрочное привлечение»;

– «Ликвидные активы / Депозиты и краткосрочное привлечение»;

– «Оставшаяся операционная прибыль» (чистая прибыль от остальных ценных бумаг (не относящихся к предназначенным для продажи и оцениваемым по справедливой стоимости через прибыль или убыток); чистый доход от страховой деятельности; прочие доходы от основной деятельности, операционная прибыль или убыток от участия);

– «Обесцененные кредиты / Сумма выданных кредитов»;

– «Коэффициент достаточности капитала»;

– «Межбанковский коэффициент» (соотношение остатков по лоро- и ностро-счетам);

– «Гудвилл»;

– «Вероятность дефолта страны». (Для оценки вероятности дефолта страны использовались присвоенные данной стране на конкретный промежуток времени рейтинги от трех международных рейтинговых агентств (Standard & Poor’s, Moody’s Investors Service и Fitch Ratings). Для соотнесения рейтингов и вероятностей дефолта использовались данные из ежегодно публикуемых рейтинговыми агентствами отчетов о вероятностях дефолтов. Здесь важно отметить, что в случае наличия у страны более одного рейтинга для определения конкретной вероятности дефолта использовались принципы, изложенные в рекомендациях «Базель II». Так, согласно пункту 97, в случае если у контрагента имеется рейтинг от двух рейтинговых агентств, используется тот рейтинг, которому соответствует наибольшая вероятность дефолта (то есть худший рейтинг). Если же у контрагента имеется более двух рейтингов (в нашем случае это количество ограничивается тремя), то, согласно пункту 98, отбирается два рейтинга, соответствующих наименьшей вероятности дефолта, и уже из них выбирается тот, которому соответствует большая вероятность дефолта (то есть из трех рейтингов вначале выбираются два лучших, а затем из них выбирается худший). Подобная оценка позволила получить конкретное значение вероятности дефолта каждой страны для каждого временного периода оценки);

– «Наличие государственного участия в акционерном капитале банка» (фиктивная переменная, принимающая значение «1», если государство входит в какой-то части в акционерный капитал банка, и «0», если нет);

– «Принадлежность к стране» (несколько фиктивных переменных, принимающих значение «1», если данный банк относится к той стране, которую характеризует данная переменная).

Еще одной часто встречающейся сложностью при отборе показателей является наличие гетероскедастичности (неоднородность наблюдений, выражающаяся в непостоянной дисперсии случайной ошибки модели). Поскольку в представленной выборке большое количество переменных принимает абсолютное, а не относительное значение, хорошим способом избавления от проблемы наличия гетероскедастичности является попытка взять от абсолютных значений натуральный логарифм. Переход к логарифму позволяет приблизить распределение остатков регрессии к нормальному распределению. Это повлияет на трактовку полученных результатов, но не изменит общей сути вычислений.

Из первоначального списка анализируемых переменных три были видоизменены. От двух абсолютных переменных был взят их натуральный логарифм: «Итого активы» и «Гудвилл». Это говорит о том, что теперь эти переменные следует трактовать в терминах эластичности: «Изменение итого активов» и «Изменение гудвилла».

Переменная «Оставшаяся операционная прибыль» была приведена к относительному виду путем ее соотношения с показателем «Итого активы». Полученная переменная получила название «Доля оставшейся операционной прибыли в активах».

Новые переменные также были проверены на наличие автокорреляции со всеми остальными, и были получены приемлемые результаты.

Окончательный набор переменных представлен в таблице 3.

Важно пояснить, что не все банки на регулярной основе публикуют ежеквартальные отчетности, но так как банки, на долг которых торгуются CDS, являются, как правило, достаточно крупными и публичными, то больших трудностей при сборе информации по данной выборке эта проблема не составила. Однако по тем показателям отчетности, по которым по той или иной причине данные отсутствовали, выборка была восполнена посредством вычисления средневзвешенного изменения пропущенного показателя по всем банкам из одной страны из представленной выборки за данный период. Это позволило добиться высококачественной по заполняемости выборки.

Отметим также, что все данные финансовой отчетности брались на фактическую дату составления отчетности. Полученные показатели сравнивались со значениями спредов CDS за этот день. Очевидно, что отчетности не публикуются в тот же день, когда они составляются, однако мы исходим из предпосылки о том, что все инвесторы получают информацию в тот же день, на который формируются отчетности. Опущение этой предпосылки и исследование модели с учетом даты публикации отчетности является хорошей возможностью для совершенствования модели в будущем.

Таблица 3

Набор переменных регрессионной модели оценки теоретического спреда CDS

Исходная модель оценки теоретического спреда CDS коммерческого банка выглядит следующим образом:

y_it = α + β₁*x_1,it + β₂*x_2,it + … + β_n*x_n,it + υ_it,

i = 1,…,N; t = 1,…,T, (1)

где

i – номер объекта,

t – время,

y_it – объясняемая переменная,

α – свободный член,

β_n – коэффициент при объясняющей переменной,

x_n,it – объясняющая переменная,

υ_it – случайная ошибка.

По ходу исследования будут построены четыре вида моделей:

1. линейная регрессионная модель;

2. модель панельных данных «between»-регрессии;

3. модель с детерминированными эффектами;

4. модель со случайными эффектами.

Практическое исследование

Линейная регрессионная модель является сквозной регрессией по всем временным периодам и по всем банкам, не учитывает панельную структуру данных. Оценка проводится с помощью метода наименьших квадратов. Надо отметить, что анализируемые данные имеют явный вид панельных данных (большое количество банков с некоторым количеством переменных за несколько временных периодов), следовательно, для более точного анализа и учета специфических характеристик различающихся банков лучше подходят модели, учитывающие панельный характер данных.

Построение простейшей регрессии линейного вида с поэтапным исключением из модели незначимых переменных привело к следующим результатам (см. таблицу 4).

Скорректированный R² принял следующее значение: R²_adj = 0,851. Общее количество наблюдаемых данных составило 373 наблюдения. Анализируя полученные результаты, следует отметить следующее:

1. Переменная «Суверенный спред CDS» значима (на 1%-ом уровне значимости), что свидетельствует о ее сильной объяснительной способности. При этом влияние этой переменной положительно, что логично: спред CDS банка почти всегда превышает суверенный спред.

2. Также значимыми оказались фиктивные переменные модели: «Наличие государственного участия в акционерном капитале банка» (на 10%-ом уровне значимости) и «Принадлежность к стране» (1%-ый уровень значимости для всех стран, кроме России (5%-ый уровень значимости)).

3. Следующие три переменные значимы, и коэффициенты при них имеют отрицательное значение: «Изменение итого активов», «Кредиты за вычетом резервов / Итого активы» и «Коэффициент достаточности капитала» (все – на 1%-ом уровне значимости). Что вполне логично и объяснимо: рост активов, доли кредитов в активах и коэффициента достаточности капитала, при прочих равных, положительным образом влияют на восприятие банка инвесторами.

4. С другой стороны значимы, и коэффициенты положительны у следующих переменных: «Чистая процентная маржа» (на 1%-ом уровне значимости), «Средняя рентабельность активов» (на 5%-ом уровне значимости), «Кредиты за вычетом резервов / Депозиты и краткосрочное привлечение» и «Изменение гудвилла» (обе – на 1%-ом уровне значимости). При этом если то, что рост кредитов по сравнению с депозитами оказывает отрицательное влияние на восприятие банка инвесторами, вполне логично, то отрицательная зависимость от роста маржи и рентабельности, а также роста гудвилла вызывает вопросы. Однако это влияние может измениться при применении моделей, учитывающих панельный вид данных.

Отметим, что проведенные тесты на автокорреляцию и гетероскедастичность показали, что полученные результаты можно считать приемлемыми.

Таблица 4

Оценивание регрессии линейного вида

Модель панельных данных «between»-регрессии представляет собой переписанную в терминах усредненных по времени значений переменных исходную модель, которая оценивается с помощью метода наименьших квадратов. Полученные по этой модели результаты показывают, как влияют на усредненную по времени зависимую переменную усредненные по времени для каждого объекта объясняющие переменные.

В данном случае надо смотреть на R²_between; величина этого показателя (R²_between = 0,998) свидетельствует о том, что при тестировании такой модели возникает много проблем. В связи с этим представляется нецелесообразным подробно анализировать ее результаты, отметим только, что «between»-регрессии часто являются вспомогательными.

Высокое значение R²_between свидетельствуют о том, что изменение средних по времени показателей для каждого банка оказывает более существенное влияние на каждую переменную, чем временные колебания этих показателей относительно средних.

Модель с фиксированными эффектами, «within»-регрессии (fixed effects model) характеризуется тем, что ненаблюдаемые случайные эффекты в ней (то есть объясняющие переменные, которые по тем или иным причинам не были включены в модель) – это фиксированные параметры, а случайная составляющая в регрессии является независимой одинаково распределенной случайной величиной. Важно, что эта независимость должна заключаться в том, что все объясняющие переменные, включенные в модель, должны быть полностью независимы от этих случайных величин для любого банка в любой момент времени.

Регрессия «within» – это исходная регрессионная модель, переписанная в терминах отклонений от средних по времени значений переменных. Надо отметить, что такие коэффициенты можно оценить только при неинвариантных по времени регрессорах, следовательно, применение фиктивных переменных в данной модели невозможно. Оценивание производится обыкновенным методом наименьших квадратов.

Результаты тестирования модели выглядят следующим образом (см. таблицу 5).

Таблица 5

Оценивание модели с фиксированными эффектами

О качестве моделей следует судить по коэффициентам детерминации R²_within – 0,817. Количество наблюдений – 390. Можно сделать вывод, что динамические различия оказывают существенное влияние на объясняющую переменную.

К основным особенностям полученной модели можно отнести следующие:

1. Так же, как и при оценивании сквозной регрессии, коэффициент при переменной «Суверенный спред CDS» оказался значимым (на 1%-ом уровне значимости) и имеет положительное влияние на спред CDS банка-контрагента.

2. В отличие от сквозной регрессии коэффициент при переменной «Вероятность дефолта страны, к которой относится банк» значим (на 1%-ом уровне значимости) и также оказывает положительное влияние на спреды CDS. Что логично: чем выше вероятность дефолта страны, к которой относится банк, тем хуже оценка данного банка внешними инвесторами.

3. К переменным, влияние которых также значимо (на 1%-ом уровне значимости) и по обеим моделям осталось без изменений, можно отнести «Изменение итого активов» (коэффициент с отрицательным знаком) и «Кредиты за вычетом резервов / Депозиты и краткосрочное привлечение» (коэффициент с положительным знаком). По-прежнему, чем больше банк, тем лучше его оценивают внешние инвесторы. И чем выше доля кредитов по отношению к краткосрочным депозитам, тем, при прочих равных, хуже внешняя оценка.

4. По одной переменной влияние по сравнению со сквозной регрессией изменилось на противоположное. Коэффициент при регрессоре «Чистая процентная маржа» имеет на этот раз отрицательный коэффициент (на 1%-ом уровне значимости), что логично, так как чем больше маржа, тем, при прочих равных, лучше оценка внешними инвесторами.

5. Влияние еще двух переменных осталось без изменений, но коэффициенты при них оказались незначимыми: «Средняя рентабельность активов» и «Коэффициент достаточности капитала».

6. Отметим также общее сокращение количества объясняющих переменных, которые являются значимыми (12 в линейной модели и 5 в регрессии «within»).

Модель со случайными эффектами (random effects model) предполагает, что все индивидуальные эффекты рассматриваемых объектов случайны. Тогда можно утверждать, что объекты выборки не зависят от ненаблюдаемых случайных эффектов и случайной составляющей для любого объекта в любой момент времени. Именно данная модель в теории должна наиболее эффективно объяснять зависимости в представленной выборке. Оценивание производится обобщенным методом наименьших квадратов.

Модель со случайными эффектами можно рассматривать как компромисс между сквозной регрессией, налагающей сильное ограничение гомогенности (заключающуюся в однородности выборки) на все коэффициенты уравнения регрессии, и регрессией с фиксированными эффектами, которая позволяет для каждого объекта выборки ввести свою константу (среднюю) и, таким образом, учесть существующую в реальности, но не наблюдаемую гетерогенность (заключающуюся в неоднородности выборки, состоящей из неоднородных объектов).

Поиски такого компромисса вызваны двумя причинами: во-первых, оценки модели «within» хотя и состоятельны для статических моделей в отсутствии эндогенности, но часто не очень эффективны с экономической точки зрения, и во-вторых, модель «within» не позволяет оценивать коэффициенты при инвариантных по времени регрессорах, которые тоже могут играть достаточно большую роль (то есть фиктивных переменных).

Поэтапное исключение из модели незначимых переменных привело к следующей итоговой модели со случайными эффектами (см. таблицу 6):

Таблица 6

Оценивание окончательной модели со случайными эффектами

При интерпретации моделей со случайными эффектами следует опираться не на R², так как в регрессии, оцененной с помощью обобщенного метода наименьших квадратов, он уже не является адекватной мерой качества модели. О значимости регрессии в целом свидетельствует высокое значение статистики Вальда – 1594,92 (на 1%-ом уровне значимости). Общее количество наблюдений составило 390.

Итоговое сравнение влияния всех регрессоров на объясняемую переменную во всех моделях приведено в таблице 7.

Из приведенного сравнения результатов моделей сделать следующие выводы:

1. «Суверенный спред CDS» всегда значим и его влияние положительно. Это доказывает первоначальную гипотезу о том, что «Спред CDS» банка-контрагента состоит из суверенного спреда плюс определенная дельта.

2. «Изменение итого активов» всегда оказывает положительное влияние на оценку банка внешними инвесторами: чем больше активы, тем меньше «Спред CDS».

3. «Вероятность дефолта страны», к которой относится данный банк, также всегда положительно влияет на «Спред CDS», то есть, чем больше вероятность дефолта страны, тем хуже банк оценивают внешние инвесторы.

4. «Наличие государственного участия в акционерном капитале банка» также находит положительное отражение в оценке банка внешними инвесторами, что тоже логично.

5. Как и при первой сквозной регрессии, модель со случайными эффектами позволяет отразить уровень влияния стран на значение «Спреда CDS».

6. При рассмотрении модели со случайными эффектами значимым и положительным получился коэффициент при переменной «Доля оставшейся операционной прибыли в активах» (на 5%-ом уровне значимости). Чем выше его доля, тем хуже оценивают банк внешние инвесторы.

7. Следующие переменные имеют определенно положительное влияние на «Спред CDS», то есть рост этих показателей выглядит отрицательно в глазах внешних инвесторов: «Основные фонды / Итого обязательства» – чем больше доля основных средств в обязательствах банка, тем хуже. «Средняя рентабельность активов» – по-прежнему отрицательно взаимосвязана с оценкой внешних инвесторов. «Кредиты за вычетом резервов / Депозиты и краткосрочное привлечение» – чем соотношение кредитов к краткосрочным депозитам больше, тем хуже.

8. Следующая переменная имеет определенно негативное влияние на «Спред CDS»: «Коэффициент достаточности капитала» – чем выше уровень достаточности капитала, тем лучше.

9. Наконец есть группа регрессоров, влияние которых однозначно определить не удалось: «Чистая процентная маржа», «Коэффициент Затраты / Расходы», «Кредиты за вычетом резервов / Итого активы», «Ликвидные активы / Депозиты и краткосрочное привлечение», «Обесцененные кредиты / Сумма выданных кредитов», «Межбанковский коэффициент» и «Изменение гудвилла».

10. Влияние константы всегда положительно и значимо для всех моделей.

Таблица 7

Сравнение влияния всех регрессоров по сквозной регрессии и моделям с фиксированными и случайными эффектами

Выберем теперь наиболее адекватную нашим данным модель. Для этого проведем попарное сравнение оцененных моделей:

1. Сквозную линейную регрессию сравним с регрессионной моделью с фиксированными эффектами – тест Вальда (Wald test).

2. Сквозную линейную регрессию сравним с регрессионной моделью со случайными эффектами – тест Бройша-Пагана (Breusch-Pagan test).

3. Регрессионную модель с фиксированными эффектами сравним с регрессионной моделью со случайными эффектами – тест Хаусмана (Hausman specification test).

Тест Вальда проверяет гипотезу о равенстве нулю всех индивидуальных эффектов.

В нашем случае:

CDS5 F test that all u_i=0: F(23, 361) = 47.05 Prob > F = 0.0000

Поскольку уровень значимости меньше 1%, то основная гипотеза отвергается. Таким образом, регрессионная модель с фиксированными эффектами лучше подходит для описания данных, чем модель простой линейной регрессии.

Тест Бройша-Пагана является тестом на наличие случайного индивидуального эффекта и проверяет линейную зависимость дисперсии случайных ошибок от набора переменных. Основная гипотеза заключается в том, что эта дисперсия равна 0.

В нашем случае:

CDS5

Test: Var(u) = 0

chibar2(01) = 2172.05

Prob > chibar2 = 0.0000

Поскольку уровень значимости меньше 1%, то основная гипотеза отвергается. Таким образом, регрессионная модель со случайными эффектами лучше подходит для описания данных, чем модель простой линейной регрессии.

Тест Хаусмана позволяет сделать выбор между моделями с фиксированными и случайными эффектами. Модель со случайными эффектами может быть применима только в том случае, когда существует некоррелированность случайного эффекта с регрессорами. В тесте проверяется основная гипотеза, что такая корреляция равна 0, при альтернативной гипотезе – что их корреляция нулю не равна. Этот тест построен на разности двух оценок, полученных из регрессий с фиксированными и случайными эффектами. Первые состоятельны как в случае основной, так и в случае альтернативной гипотезы, вторые – только при основной гипотезе.

В нашем случае:

Test (CDS5): Ho: difference in coefficients not systematic

chi2(4) = (b-B)' [(V_b-V_B)^(-1)](b-B) = 2.04

Prob>chi2 = 0.7277

Поскольку уровень значимости существенно больше 1%, основная гипотеза подтверждается. Полученные результаты позволяют сделать вывод, что в нашем случае лучше подходит модель со случайными индивидуальными эффектами.

Итоговая формула модели принимает следующий вид:

CDS5_it = 1515 + 1.25*CDS5_n,it – 73.76*ltotalassets_it +

+ 74.95*ropta_it + 38.7*sum5_c,it – 178.7*b – 125.4*r – 310.4*i, (2)

где

i – номер объекта,

t – время,

CDS5_it – «Пятилетний спред CDS»,

CDS5_n,it – «Суверенный спред CDS»,

ltotalassets_it – «Изменение итого активов»,

ropta_it – «Доля оставшейся операционной прибыли в активах»,

sum5_c,it – «Вероятность дефолта страны»,

b, r, i – «Принадлежность к стране – Бразилия, Россия или Индия».

Таким образом, согласно модели, величина спреда CDS зависит от суверенного спреда CDS, изменения величины активов, доли оставшейся операционной прибыли, а также от того, к какой стране относится анализируемый банк и вероятности ее дефолта.

Сравнение теоретических спредов CDS с их фактическими значениями

После того как была построена модель оценки теоретических спредов CDS, для проверки модели на практике, оценим российские банки, CDS на долг которых торгуются на бирже. Для анализа предполагается сравнить теоретические спреды CDS с их фактическими значениями для российских банков.

С помощью приведенной в предыдущем параграфе модели были получены квартальные теоретические значения спредов CDS и затем они были сопоставлены с их фактическими значениями. В таблице 8 приведены сравнения спредов CDS на начало каждого из 5 анализируемых годов.

Из таблицы 8 видно, что в целом модель предсказывает изменения CDS верно. Но для большей наглядности обратимся к графикам. На рисунках 1‑4 представлена динамика изменения торетических (CDS5П) и фактических (CDS5Ф) спредов 5-летних CDS на Банк ВТБ, Банка Москвы, Газпромбанк и Сбербанк.

Таблица 8

Сопоставление теоретических спредов CDS с их фактическими значениями

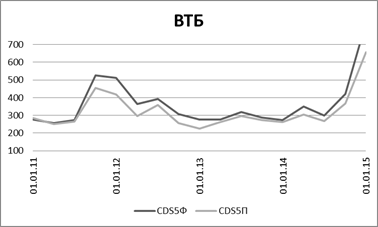
Рисунок 1. 5-летние теоретический и фактический спреды CDS на Банк ВТБ

Источник: Cоставлено автором

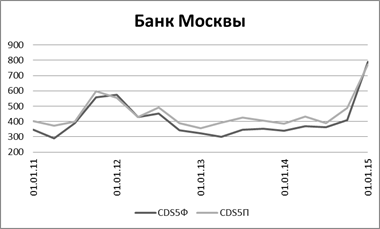
Рисунок 2. 5-летние теоретический и фактический спреды CDS на Банк Москвы

Источник: Составлено автором

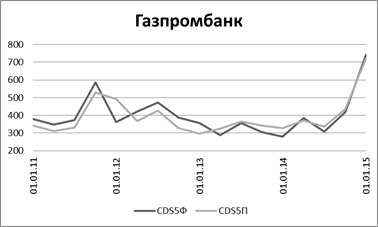
Рисунок 3. 5-летние теоретический и фактический спреды CDS на Банк ГПБ

Источник: Составлено автором

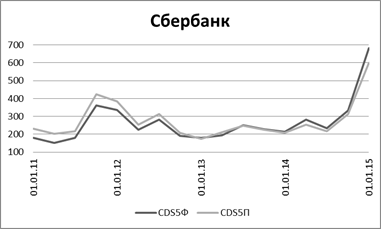
Рисунок 4. 5-летние теоретический и фактический спреды CDS на Сбербанк

Источник: Составлено автором

Обратим внимание, что в целом по представленным данным наблюдается сходство, и основные тенденции предсказываются моделью правильно. Отметим, что лучшие результаы показывают теоретические спреды на Сбербанк и Банк ВТБ, что объясняется тем, что именно CDS на долги этих двух банков являются наиболее ликвидными среди российских банков. Таким образом, показанная статистически «хорошая» объясняющая способность модели подтверждается и эмпирической проверкой, и построенными графиками.

Выводы

Основные современные методы оценки контрагентного риска на рынке межбанковского кредитования заключаются в построении различных кредитных, а также рейтинговых моделей. Новым подходом к оценке контрагентного риска является построение банком прогнозных спредов CDS для своих контрагентов.

Существенный плюс CDS заключается в том, что этот инструмент постоянно оценивают участники рынка, которые берут во внимание не только отчетность банка, его кредитные рейтинги, другие фундаментальные оценки, но и всю доступную информацию. Это значительно увеличивает гибкость в оценке контрагентного риска по сравнению с использованием рейтингов.

В настоящем исследовании была построена модель оценки CDS, базирующуюся на совмещении фундаментальной оценки с рыночной.

Для цели построения теоретических значений CDS брались те банки из развивающихся стран группы БРИКС (Бразилия, Россия, Индия, Китай и ЮАР), CDS на долговые инструменты которых котируются на рынке.

Спред CDS на конкретный банк состоит из спреда CDS на долг той страны, которую он представляет, плюс дельта, выражающаяся в определенных особенностях конкретного банка. Применяемая в исследовании модель оценки CDS основывается на фундаментальных показателях банка из финансовой отчетности, которые могут объяснить особенности каждого конкретного банка, и таким образом позволяют получить оценку теоретическую спреда CDS на данный банк.

По результатам расчетов было получено, что на величину спреда CDS оказывают влияние следующие факторы: в первую очередь суверенный спред CDS страны, которую представляет анализируемый банк, а также вероятность дефолта страны, к которой он относится, несколько факторов, характеризующих банк, – наличие или отсутствие государственного участия в акционерном капитале и то, из какой он страны, а также финансовые показатели из отчетности.

По итогам рассмотрения наиболее эффективной модели можно сделать вывод о том, что из финансовых показателей из отчетности наиболее значимыми являются следующие: изменение итоговой величины активов (обратная зависимость со спредом CDS) и доля оставшейся операционной прибыли в активах (прямая зависимость).

Полученные с помощью построенной модели оценки могут быть затем имплементированы в модель оценки вероятности дефолта банков-контрагентов, а результаты модели применимы для анализа банками своих контрагентов и последующего установления на них лимитов кредитного риска.

[1] При формировании выборки использовались следующие базы данных: Bankscope – Bureau van Dijk, Bloomberg Business и Thomson Reuters.

[2] CDS на банки из ЮАР в исследуемый в работе период представлены не были.