Современные возможности оценки кредитного риска при ипотечном жилищном кредитовании

Введение

Проблема моделирования и управления кредитными рисками в условиях динамического развития экономики и увеличения объемов кредитования становится ключевым ядром при построении эффективной системы риск-менеджмента современной кредитной организации. Среди разнообразия направлений кредитования физических лиц стоит отметить особую роль ипотечного жилищного кредитования (ИЖК), которое является одним из финансовых механизмов обеспечения населения жильем. Развитие системы ИЖК входит в число приоритетных направлений государственной жилищной политики, а согласно «Стратегии развития ипотечного жилищного кредитования в РФ до 2030» [5] ипотечный жилищный кредит станет основным инструментом обеспечения граждан жилой недвижимостью.

С внедрением элементов Базельских соглашений в национальную банковскую систему [10], включая их реализацию в «Методических рекомендациях по реализации подхода к расчету кредитного риска на основе внутренних рейтингов банков» [4], у банков появилась возможность использовать внутренние модели для оценки величины кредитного риска с целью определения величины капитала, необходимой для покрытия кредитного риска. К основным компонентам кредитного риска традиционно относят вероятность дефолта (Probability of Default, PD), долю потерь при дефолте (Loss Given Default, LGD) и сумму, подверженную риску дефолта (Exposure at Default, EAD). Цель статьи заключается в систематизации существующих подходов и методов оценки ключевых компонентов кредитного риска в приложении к ИЖК на основе существующей академической литературы и обзоров практик банковского риск-менеджмента. Особое внимание в работе уделяется особенностям данных компонентов кредитного риска и современным возможностям их учета при ипотечном андеррайтинге.

Обзор литературы

Моделирование вероятности ипотечного дефолта PD в основном базируется на двух теориях к объяснению причин ипотечного дефолта, известных как теория платежеспособности (the ability-to-pay theory) и теория опционов (the put-option theory). Появление этих теорий сопряжено со становлением таких разделов экономической науки, как теория потребления (конец 70-х гг. XX в.), институциональная экономика (конец 70-х – начало 80-х гг. XX в.), теория опционов (середина 80-х гг. XX в.) и теория портфельных инвестиций (начало 90-х гг. XX в.). В рамках данных теорий обсуждаются различные причины, побуждающие ипотечного заемщика объявлять дефолт.

В теории платежеспособности ключевая роль отводится соотношению ежемесячного платежа заемщика к размеру его ежемесячного дохода, известного как соотношение Платеж/Доход (debt-to-income ratio). Заемщик не объявляет ипотечный дефолт до тех пор, пока его доход покрывает сумму периодического ежемесячного платежа. В рамках теории платежеспособности наряду с соотношением Платеж/Доход к факторам кредитного риска относят показатели, которые связаны с его изменением. Например, увеличение финансового бремени заемщика, которое может быть спровоцировано любыми шоками его дохода, такими как потеря работы, развод, болезнь или смерть.

Согласно теории опционов заемщик объявляет ипотечный дефолт когда финансовые выгоды от такого решения превышают сопутствующие такому решению финансовые издержки. В этом случае ипотечный дефолт представляет собой исполнение опциона put (опциона на продажу) [12]. Другими словами, заемщик объявляет дефолт, если непогашенный остаток долга существенно превышает залоговую стоимость жилья. Отсюда следует, что при моделировании вероятности дефолта имеет значение соотношение суммы ипотечного кредита к стоимости залогового обеспечения, известного как показатель Кредит/Залог, а также факторы, способствующие его изменению, например, цены на рынке жилья.

Первая попытка эмпирически протестировать валидность данных теорий при моделировании вероятности ипотечного дефолта американских заемщиков была предпринята Джексоном и Кассерманом [15]. Более поздние исследования, в основном по американскому ипотечному рынку, не оставляли попыток тестирования данных теорий [7, 9, 13, 17] и позволили заключить о целесообразности использования обоих теорий для моделирования вероятности ипотечного дефолта. В эмпирической литературе находит подтверждение зависимость вероятности ипотечного дефолта от социально-демографических характеристик заемщиков, включая их уровень финансовой грамотности, параметров ипотечного кредита и макроэкономических показателей.

Для эмпирических целей в основном используется довольно широкий класс статистических (эконометрических) моделей. В зависимости от того, накладывается ли предположение о теоретическом законе распределения случайных величин, зависящего от числовых параметров, статистические модели вероятности ипотечного дефолта включают параметрические, полупараметрические и непараметрические модели. Последние теоретические разработки, вычислительная эффективность и доступность больших массивов данных обуславливает растущий интерес к полупараметрическому и непараметрическому оцениванию в финансовом моделировании. Однако стоит отметить, что в практике ипотечного андеррайтинга они менее распространены.

Для моделирования доли потерь в случае ипотечного дефолта LGD, в отличие от вероятности ипотечного дефолта PD, недостаточно наблюдать информацию в части наступления события ипотечного дефолта. При бухгалтерском подходе доля потерь при дефолте рассчитывается как:

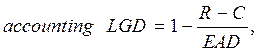(1)

где accounting LGD — бухгалтерская доля потерь при дефолте, R — взысканная в судебном порядке сумма ипотечной задолженности (сумма платежей по восстановлению), C — общие издержки по взысканию платежей, возникающие в ходе работы с просроченной задолженностью, EAD — сумма, подверженная риску дефолта, которая включает в себя средства, предоставленные заемщику и не погашенные им — текущая остаточная сумма долга, включая комиссии, штрафы и непогашенные проценты.

При экономическом подходе используется метод дисконтированных денежных потоков:

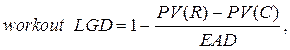(2)

где workout LGD — экономическая доля потерь при дефолте, PV(R) — приведенная к дате ипотечного дефолта стоимость взысканной в судебном порядке суммы ипотечной задолженности, PV(C) — приведенная к дате ипотечного дефолта стоимость общих издержек, возникающих в ходе работы с просроченной задолженностью.

Таким образом, в рамках обоих подходов наряду с событием ипотечного дефолта необходимо знание соответствующей стоимости залогового обеспечения и величины общих издержек, связанных с взысканием просроченной задолженности, а также остаточной суммы долга EAD. Соответственно, систематизация факторов кредитного риска в контексте LGD строится с точки зрения их влияния на вышеупомянутые компоненты LGD. В частности, эмпирические работы, включая [11, 18], указывают на влияние характеристик залогового обеспечения, параметров ипотечного кредита, особенностей процесса судебного урегулирования просроченной задолженности и макроэкономических условий. В них в основном превалирует использование эконометрических (регрессионных) моделей в классе параметрических, несмотря на существование ряда отличительных особенностей распределения LGD (например, бимодальности и цензурированности).

Особенности моделирования вероятности ипотечного дефолта

Одна из особенностей моделирования вероятности ипотечного дефолта заключается во взаимосвязанности принятий решений участников ипотечной сделки. В первую очередь, это касается решения кредитора об одобрении/отклонении кредитной заявки, принимаемое в результате ипотечного андеррайтинга, и решения заемщика объявлении/необъявлении ипотечного дефолта в ходе обслуживания ипотечного жилищного кредита. В настоящее время не существует международно-согласованных стандартов по кредитному андеррайтингу и выдаче ипотечных кредитов. Экспертный обзор практик ипотечного андеррайтинга может быть найден в [6]. Среди общих принципов ипотечного андеррайтинга следует отметить следующие:

1) эффективное подтверждение доходов и финансовой информации;

2) разумное покрытие для обслуживания долга (расчет соотношения размера ежемесячного платежа к ежемесячному доходу заемщика (соотношение Платеж/Доход; Debt-To-Income ratio, DTI);

3) реалистичные выплаты по ипотечным кредитам, удовлетворяющим установленным критериям;

4) надлежащие значения соотношения суммы кредита к оценочной стоимости приобретаемого жилья (соотношение Кредит/Залог; Loan-To-Value Ratio, LTV);

5) эффективное управление оценкой залога;

6) использование ипотечного страхования;

7) разумные допущения в отношении возможных негативных событий в связи с изменениями на рынке жилья, изменениями личных обстоятельств заемщика или микроэкономической конъюнктуры;

8) минимальные приемлемые стандарты;

9) практика выплаты вознаграждений (например, вознаграждение менеджеров по оценке кредитного риска не должно зависеть от объемов продаж).

В процессе кредитного андеррайтинга принимают участие специалисты разных структурных подразделений кредитной организации, включая юридическое управление, управление кредитования частных клиентов, финансовое управление и управление рисков, управление безопасности, а также отдел розничных продаж, отдел рефинансирования и др.

Игнорирование взаимосвязанности процессов принятия решений при эконометрическом моделировании PD порождает эконометрическую проблему, известную как проблема выборочной селективности. Вследствие этого, полученные оценки параметров регрессионного уравнения для вероятности ипотечного дефолта не обладают всеми желаемыми свойствами оценок, в частности, становятся смещенными и/или несостоятельными. Вместе с тем такая проблема может быть решена путем использования существующих разработок в области эконометрического моделирования. Так, в академической литературе, посвященной оценке кредитного риска при ИЖК, широкое распространение получил класс моделей Хекмана [14], основная идея которых сводится к моделированию нескольких взаимосвязанных процессов принятия решений. Другими словами, вместо одномерной эконометрической модели вероятности ипотечного дефолта оценивается двумерная эконометрическая модель, содержащей в себе уравнение регрессии для вероятности одобрения ипотечной заявки и вероятности ипотечного дефолта. Как показано в эмпирической работе [19] на примере американского ипотечного рынка, большинство оценок параметров в уравнении для вероятности одобрения ипотечного заемщика имеют противоположный знак в уравнении для вероятности дефолта, однако это верно только после коррекции оценок на выборочную селективность.

Результаты апробации многомерной эконометрической модели вероятности ипотечного дефолта заемщиков для портфеля ипотечных кредитов регионального оператора ОАО «Агентства по ипотечному жилищному кредитованию», включающей наряду с вероятностями одобрения ипотечной заявки и ипотечного дефолта, также вероятности подачи ипотечной заявки и заключения кредитного договора клиентом, обсуждаются в работах [2, 3]. В эмпирической работе [20] находит применение расширение классической модели Хекмана, которая используется для выявления взаимосвязи процесса кредитного андеррайтинга и процесса ценообразования при ИЖК.

Оценка потерь при ипотечном дефолте в условиях ограниченности информации

Для оценки доли потерь при ипотечном дефолте могут быть использованы вышеописанные бухгалтерский и экономический подходы. Однако их использование в практике банковского риск-менеджмента, в первую очередь, усложняется проблемой асимметрии информации, возникающей на разных процессах ИЖК. Это касается не только ограниченности информации о кредитных историях потенциальных заемщиков, но и возможные трудности к получению информации по дефолтным ипотечным кредитам, включая составляющие в формулах (1) и (2), используемым для оценки величины LGD.

Для аппроксимации бухгалтерской исторической доли потерь при дефолте в условиях ограниченности информации о дате ипотечного дефолта рассмотрим метод, состоящий из нескольких последовательных этапов:

1. Эконометрическое моделирование вероятности ипотечного дефолта PD с целью получения ее прогнозных значений на исследуемом временном горизонте.

2. Аппроксимация залоговой стоимости обеспечения R, остаточной суммы долга EAD и издержек, связанных с процессом взыскания просроченной ипотечной задолженности C на исследуемом временном горизонте.

3. Вычисление математического ожидания доли потерь при ипотечном дефолте LGD, которое служит аппроксимацией исторической доли потерь при ипотечном дефолте.

Практическая реализация данного метода невозможна без использования ряда ограничительных допущений. В условиях судебного урегулирования просроченной ипотечной задолженности требуются предположения не только о величине общих издержек и сроке восстановления, а также о стоимости реализации залогового обеспечения, включая размер дисконта и др. Кроме того, следует учитывать как особенности российского законодательства, которые определяют порядок обращения взыскания на залоговое имущество, так и банковскую и судебную практику. Так, например, реализация заложенного имущества допускается не ранее чем через 10 дней с момента получения залогодателем и заемщиком уведомление о начале обращения взыскания на предмет залога, а при наличии уважительных причин реализация предмета залога может быть отсрочена до 1 года. На практике, процесс взыскания довольно и может составлять до 1,5–2 г. [6].

Оценка экономической доли потерь LGD требует также предположений о размере ставки дисконтирования, которая в разные периоды экономического цикла различна. Поэтому выделяют также циклический LGD (point-in-time, PIT), который рассчитывается по краткосрочным периодам наблюдений и зависит от экономического цикла; долгосрочный LGD (trough-the-cycle, TTC), который соответствует нециклическому сценарию и не зависит от времени оценки LGD; LGD в период спада в экономическом цикле (bottom-of-the-cycle, downturn LGD). При расчете последнего, от кредитных организаций требуется не только выявление периодов экономического спада, но и определение их эффекта на показатель PD с последующим учетом его при расчете величины LGD [16]. Наличие проциклического эффекта в российском банковском секторе от внедрения Базель II, который обсуждается, например, в работе [1], может оказать нежелательное воздействие на экономику в целом, если в период спада капитал банков будет ограничен, и они будут вынуждены, таким образом, сократить кредитование в ситуации, когда оно в большей степени необходимо.

Отметим также, что в целях минимизации ошибок аппроксимации требуется не только использование реалистичных предпосылок, но и анализ устойчивости полученных результатов в случае их ослабления или нарушения. Например, в работе [8] демонстрируется высокая чувствительность величины экономического LGD к использованию различных предположений о размере ставки дисконтирования.

Полученные результаты аппроксимации исторической доли потерь при ипотечном дефолте позволяют также получить картину о распределении потерь внутри кредитного портфеля. В литературе отмечается возможная неоднородность потерь при ИЖК [8]. Об этом свидетельствует несимметричность и бимодальность распределения LGD, которая также прослеживается и на рис. 1 для портфеля ипотечных кредитов регионального оператора АИЖК. На рис. 1 можно заметить концентрацию доли потерь в окрестности 0,1 и 0,5, которые во многом определяются низким и высоким соотношением Кредит/Залог соответственно. Это означает, что заемщики с более высоким соотношением Кредит/Залог имеют более высокую ожидаемую долю потерь в случае дефолта, а, следовательно, и более высокий уровень кредитного риска.

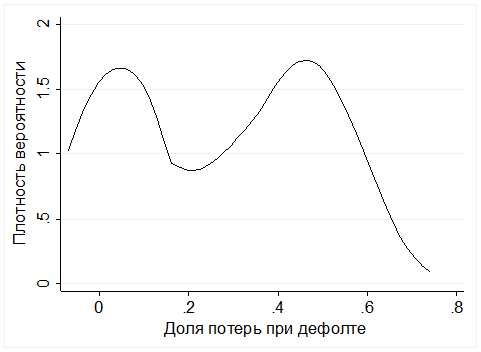
Рисунок 1. Распределение аппроксимированной исторической доли потерь LGD

Источник: составлен автором.

Неоднородность распределения потерь во многом связана с разным уровнем возмещения потерь в случае ипотечного дефолта, в основном посредством реализации залогового обеспечения. Такие результаты позволяют классифицировать ипотечных заемщиков по уровню кредитного риска, что может найти отражение в кредитной политики банка, включая направления по развитию адаптивных внутренних моделей оценки кредитного риска и совершенствование банковских продуктов. В целом, оценка доли потерь при дефолте представляется не менее комплексной задачей, чем моделирование вероятности дефолта, которая требует активного участия различных структурных подразделений банка, которые не ограничиваются подразделением по управлению рисками.

Заключение

Совершенствованию системы банковского риск-менеджмента способствует повышение точности оценки кредитного риска, включая его оценку в рамках внутренних рейтинговых моделей. Это требует не только развития, подходов и методов количественной оценки основных компонентов кредитного риска (вероятности дефолта, доли потерь в случае и дефолта, суммы, подверженной риску дефолта) с учетом особенностей различных видов кредитования, но и их эффективного внедрения в практику кредитного андеррайтинга. Современные возможности оценки кредитного риска при ипотечном жилищном кредитовании позволяют использовать широкий класс инструментов количественного анализа, включая эконометрическое моделирование. Они позволяют не только учесть природу исследуемых случайных величин, но и особенности процесса ипотечного андеррайтинга и современной системы ипотечного жилищного кредитования в России. В основном такие разработки нашли применение в академической литературе, посвященной проблемам кредитного риска и ипотечного кредитования в приложении к зарубежным рынкам. Несмотря на то, что они гораздо в меньшей степени встречаются в практике ипотечного андеррайтинга российских коммерческих банков, существующие инициативы регуляторов по развитию и внедрению IRB-подхода позволяет заключить о перспективах их активного использования.