Совершенствование методологии применения закона Бенфорда в системе аудиторских процедур диагностики недобросовестных действий

Введение

В условиях цифровизации бизнеса и возрастающей сложности финансово-хозяйственных операций особую актуальность приобретает противодействие недобросовестным действиям участников экономических отношений. Международные исследования, проведенные Ассоциацией сертифицированных исследователей мошенничества (ACFE) и аудиторской компанией PricewaterhouseCoopers (PwC) за период 2022-2024 гг., демонстрируют значительные масштабы данного явления: практически половина (46%) компаний подвергается различным формам недобросовестных действий, что приводит к существенным финансовым потерям (в среднем 5% от годовой выручки) [11, 20]. Данная статистика не только подчеркивает системный характер проблемы, но и указывает на необходимость разработки эффективных механизмов выявления и предотвращения недобросовестных действий в корпоративном секторе.

Внешний аудит выступает одним из ключевых инструментов обеспечения прозрачности деятельности организации и защиты интересов ее стейкхолдеров. Помимо основной функции, заключающейся в выражении мнения о достоверности финансовой отчетности, современный институт аудита призван выполнять более широкий спектр задач. В частности, особую значимость приобретает выявление признаков потенциальных или реальных недобросовестных действий. Немодифицированное аудиторское заключение все чаще интерпретируется пользователями финансовой отчетности не только как формальное подтверждение отсутствия существенных искажений, но и как индикатор надежности системы внутреннего контроля организации и отсутствия фактов корпоративного мошенничества.

В то же время, международная практика свидетельствует о низкой результативности внешнего аудита в обнаружении недобросовестных действий. На рисунке 1 представлено процентное соотношение методов выявления недобросовестных действий согласно исследованию «Report to the Nations» профессиональной ассоциации ACFE, которое основано на опросе 1 921 компаний по всему миру [11]. Данные демонстрируют, что внешний аудит оказывается эффективным лишь в 3% случаев. Примечательно, что даже случайное обнаружение недобросовестных действий происходит чаще – в 5% случаев. Наиболее результативным механизмом является информирование со стороны внутренних или внешних источников. Практически половина (43%) всех недобросовестных действия была выявлена именно этим способом.

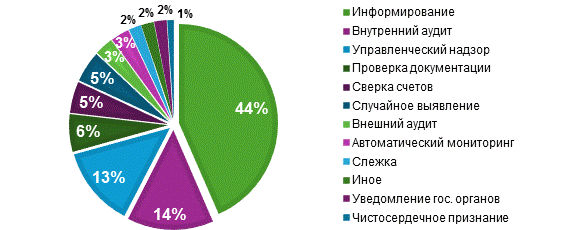
Рисунок 1. Методы выявления недобросовестных действий, ACFE, 2024 год

Источник: составлено автором на основе [11].

Учитывая, что недобросовестные действия могут приводить к существенным искажениям финансовой отчетности, международные стандарты аудита содержат требования по их обязательному рассмотрению в ходе проведения процедур оценки рисков и дальнейших аудиторских процедур по существу. Так, международный стандарт аудита 240 «Обязанности аудитора в отношении недобросовестных действий при проведении аудита финансовой отчетности» (далее – МСА 240) устанавливает обязанности по выявлению и оценке рисков существенного искажения вследствие недобросовестных действий (далее – РСИНД), планированию ответных аудиторских процедур и придерживанию принципа профессионального скептицизма на протяжении всего аудита [5, п. 11]. Система аудиторских процедур в ответ на РСИНД включает, как минимум, проверку надлежащего характера бухгалтерских записей и прочих корректировок, анализ оценочных значений на предвзятость и изучение операций за рамками обычной деятельности [5, п. 32]. Среди указанных процедур наибольшей информативностью и комплексностью характеризуется первая процедура, известная в профессиональном сообществе как тест проводок (англ. Journal Entry Testing).

В современной аудиторской практике для реализации данной процедуры преимущественно используются методы ручной обработки и фильтрации по базовым признакам, приведенным в качестве примеров в МСА 240 (операции в выходные дни, на круглые суммы, внесенные нестандартными пользователями и пр.) [5, 9]. Такой подход, несмотря на широкое распространение, демонстрирует крайне низкую эффективность в выявлении сложных и тщательно замаскированных недобросовестных действий. Более того, вследствие значительных объемов отобранных операций их ручной анализ зачастую практически неосуществим, что приводит к формальному выполнению процедуры и отсутствию какой-либо уверенности по ее результатам.

Вследствие указанных ограничений приобретает значимость применение закона Бенфорда как статистического метода, позволяющего идентифицировать скрытые закономерности и характеристики, указывающие на наличие признаков потенциальных недобросовестных действий, в том числе тщательно замаскированных. В исследованиях зарубежных ученых [13, 17, 21, 24] предложен комплекс статистических тестов, основанных на законе Бенфорда, с целью выявления аномальных элементов в выборочных совокупностях большого объема. В то же время, практическое применение указанных тестов в ходе аудита финансовой отчетности демонстрирует необходимость их дальнейшего методологического развития. В частности, получаемые результаты характеризуются неоднозначностью с точки зрения интерпретации, внутренней противоречивостью и оставляют значительный объем операций, требующих дополнительной аналитической обработки [22].

Указанный научный пробел обусловил цель данного исследования, которая заключается в совершенствовании методологии применения закона Бенфорда для выявления недобросовестных действий в данных бухгалтерского учета, а также ее адаптации к специфическим особенностям аудиторской деятельности в соответствии с требованиями международных стандартов аудита.

Материалы и методы

В контексте исторического развития закона Бенфорда (реже именуемого как закон первой цифры или закон аномальных чисел) примечательно, что его первооткрывателем является не Фрэнк Бенфорд, чьим именем он назван, а американский астроном и математик Саймон Ньюком. В 1881 году С. Ньюком обратил внимание на неравномерный характер износа страниц логарифмических таблиц: начальные страницы, содержащие числа с первыми цифрами 1 и 2, были значительно более изношены по сравнению с последующими. На основе данного эмпирического наблюдения и последующих математических расчетов, основанных на свойствах логарифмов, С. Ньюком рассчитал вероятности появления цифр в первом и во втором разрядах [15].

Данное открытие более чем на полвека опередило независимое исследование американского инженера компании General Electric Фрэнка Бенфорда, который в 1938 году опубликовал в издании «Труды Американского философского общества» научную статью под названием «Закон аномальных чисел» [12]. Значимость работы Ф. Бенфорда заключалась в проведении масштабного эмпирического исследования распределения первых цифр на основе 20 различных наборов данных. Анализируемые массивы включали широкий спектр показателей – географические объекты (протяженность рек, площади территорий), демографические данные (численность населения), математические последовательности ( , , ), а также 342 уличных адреса из справочника «Люди науки Америки». Результаты исследования продемонстрировали варьирующуюся степень соответствия различных наборов данных предполагаемому закону, однако агрегированное распределение всех массивов продемонстрировало значительное сходство с теоретическим.

На основе интегрального исчисления Ф. Бенфорд вывел формулы для вычисления ожидаемых частот появления первой ( ) и второй ( ) цифр, а также их комбинаций ( ) для любой системы счисления ( ) (таблица 1). В практике применения закона Бенфорда преимущественно рассматривается десятичная система счисления, поэтому в формулах используется десятичный логарифм ( ).

Таблица 1. Формулы ожидаемых частот первых цифр в соответствии с законом Бенфорда

В соответствии с представленными формулами, на рисунке 2 изображено распределение Бенфорда для первой цифры, второй цифры и первых двух цифр.

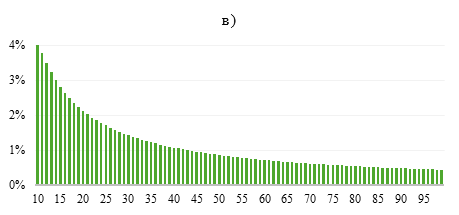
Рисунок 2. Распределение Бенфорда для а) первой цифры; б) второй цифры; в) первых двух цифр

Источник: составлено автором на основе [17].

В развитие теоретических аспектов закона Бенфорда существенный вклад внесли исследования американских математиков Р. Пинкхема (1961 г.) и Т. Хилла (1995 г.) [14, 19]. Теоретическое обоснование данного закона базируется на взаимосвязи вероятностных распределений в эмпирических данных и специфике математической структуры логарифмической шкалы. Процессы окружающего мира подвержены многочисленным ограничениям физического, природного, социального и экономического характера, что обуславливает более высокую вероятность появления малых значений по сравнению с крупными. Например, озер больше, чем рек; рек больше, чем морей; морей больше, чем океанов.

При этом закон Бенфорда применим только к совокупностям, которые удовлетворяют ряду существенных условий. В состав обязательных характеристик относятся числовой тип данных, их случайная природа, однородность явления с единым масштабом и единицами измерения, отсутствие минимальных и максимальных ограничений (за исключением нуля) и стремление распределения выборки к экспоненциальному. Кроме того, возможно выделить дополнительные условия, способствующие повышению точности и валидности результатов. В частности, значительный объем выборки (не менее 1 000 элементов), наличие величин нескольких порядков (более трех), преобладание малых элементов над крупными, а также близость логарифма разности между крайними значениями выборки к целому числу [3, 7].

Первое применение закона Бенфорда в качестве инструмента выявления мошенничества было предложено американским экономистом Хиллом Варианом в 1972 году [23]. Методологический подход Х. Вариана основывался на сопоставлении частотных распределений первой цифры в социально-экономических показателях с распределением Бенфорда для выявления аномальных отклонений. Впоследствии многие исследования приобрели характер отдельных наблюдений за тем, что конкретные наборы данных соответствуют распределению Бенфорда.

В течение последних десятилетий значительный вклад в развитие методологии применения закона Бенфорда для выявления манипуляций в бухгалтерском учете, финансовой и налоговой отчетности внес профессор Университета Западной Вирджинии Марк Нигрини. В докторской диссертации 1992 года «Выявление уклонения от уплаты подоходного налога с помощью анализа цифрового распределения» ученый применил закон Бенфорда к анализу сумм налоговых деклараций для идентификации недобросовестных налогоплательщиков. В работе 2012 года «Закон Бенфорда: методы применения в форензике, аудите и обнаружении мошенничества» М. Нигрини обобщил многочисленные исследования и представил комплексную методологию статистической обработки финансовых данных на основе закона Бенфорда.

Основополагающим принципом идентификации признаков фальсификации данных является сравнительный анализ эмпирического распределения частот первых значащих цифр исследуемого массива с теоретическим распределением Бенфорда. Данный анализ реализуется как посредством визуальной оценки гистограмм, так и путем реализации статистических тестов. В отечественной научной литературе преимущественно описывается лишь 6 базовых тестов: анализ частоты первой цифры, первой и второй цифры, первой пары цифр, первой тройки цифр, а также анализ дублей и округлений [1, 2, 7]. При этом на законе Бенфорда основаны только первые четыре теста. В международной практике методология анализа данных с помощью Бенфорда получила гораздо большее развитие. Наиболее комплексный подход, предложенный М. Нигрини, включает классификацию статистических тестов на три категории: базовые, продвинутые и связанные (рисунок 3). Выбор конкретных тестов определяется спецификой решаемой задачи и объемом имеющихся данных. В общем случае тесты выполняются последовательно.

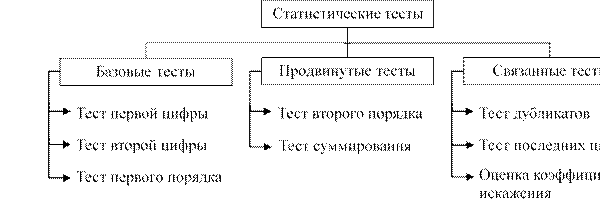
Рисунок 3. Распределение Бенфорда для а) первой цифры; б) второй цифры; в) первых двух цифр

Источник: составлено автором на основе [17].

Базовые тесты являются простыми в реализации и наглядными, вследствие чего наиболее часто используются при проверке соответствия данных распределению Бенфорда. К ним относятся тест первой цифры, тест второй цифры и тест первых двух цифр (также известный как тест первого порядка). При проведении базовых тестов анализ положительных и отрицательных чисел осуществляется раздельно, что обусловлено различной мотивацией к их манипулированию (например, тенденция к завышению прибыли при одновременном занижении убытков). Предварительным этапом является исключение чисел менее 10 ввиду их статистической несущественности.

Продвинутые тесты позволяют производить более детальный анализ и, согласно подходу М. Нигрини, включают тест суммирования и тест второго порядка. Преимуществом данных тестов является возможность применения к различным наборам данных, даже в случаях предполагаемого несоответствия закону Бенфорда. Тест суммирования направлен на выявление аномально крупных сумм чисел в разрезе первых цифр, фактически представляя собой расширенную версию теста первого порядка. Тест второго порядка анализирует первые цифры разностей между предварительно отсортированными суммами. Ввиду схожего характера выполняемых задач, в дополнение к указанным тестам целесообразно включить тест мантисс, который в методологии М. Нигрини вынесен за рамки системы, представленной на рисунке 3. Тест предполагает, что при соответствии распределения данных закону Бенфорда мантиссы (дробные части) логарифмов должны быть равномерно распределены по единичной окружности, а центр тяжести должен стремиться к точке с координатами (0; 0).

Связанные тесты представляют собой комплекс дополнительных методов, не основанных на законе Бенфорда, но исследующих прочие специфические характеристики цифрового распределения. В их состав входят тест дубликатов, позволяющий идентифицировать наиболее частотные суммы операций, тест последних двух цифр, исследующий равномерность распределения цифр в правой части чисел, а также оценка коэффициента искажения, направленная на выявление систематического завышения или занижения данных в исследуемой выборке.

Оценка соответствия фактического распределения закону Бенфорда осуществляется не только эмпирическими, но расчетными методами. Для количественной оценки применяется ряд статистических характеристик, каждая из которых обладает особенностями применения и интерпретации результатов. В научной литературе предлагаются три основные показателя, представленные в таблице 2.

Таблица 2. Статистические характеристики, оценивающие соответствие распределению Бенфорда

Результаты и обсуждение

В текущем исследовании методологический подход, предложенный М. Нигрини и другими зарубежными учеными, апробирован в ходе проведения аудиторских проверок и согласованных процедур, связанных с аналитикой данных бухгалтерского учета. Реализован комплекс базовых, продвинутых и связанных тестов с сопутствующим расчетом статистических характеристик на массиве данных, охватывающим более 30 действующих хозяйствующих субъектов. В целях обеспечения репрезентативности исследования выборка охватила различные отрасли экономики: производство, телекоммуникацию, оптовую и розничную торговлю, а также строительство, которое традиционно рассматривается как отрасль с повышенным риском недобросовестных действий [10]. Исследование продемонстрировало ряд существенных ограничений и недостатков, которые препятствуют внедрению данного подхода в качестве полноценной аудиторской процедуры в ответ на РСИНД.

Наиболее значимый недостаток заключается в отсутствии четко формализованного подхода к идентификации подозрительных операций на основе результатов тестирования. В научной литературе, как правило, предлагается метод отбора операций, начинающихся с цифр, которые имеют статистически значимые отклонения от теоретического распределения Бенфорда [2, 7, 13, 16]. Однако при его практической реализации обнаруживаются значительные сложности. Во-первых, подход невозможно применить к результатам продвинутых тестов и ряда связанных тестов, реализующих анализ не на уровне конкретных операций, а всей совокупности в целом. Во-вторых, неопределенность вносит множественность статистических характеристик, оценивающих соответствие закону Бенфорда (помимо представленных в таблице 2, можно выделить еще более 10). В большинстве исследований отбор производится только на основе Z-статистики первых значащих цифр, что фактически нивелирует значимость остальных показателей. И, в-третьих, подобный подход не обеспечивает достаточного сужения выборки, что обуславливает необходимость дополнительной аналитической обработки полученных результатов с помощью других методов. Для иллюстрации указанных ограничений рассмотрим результаты применения теста первых двух цифр (первого порядка) к массиву бухгалтерских записей дорожно-строительной компании (рисунок 4).

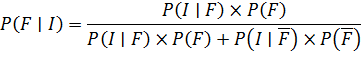
Рисунок 4. Результаты теста первого порядка в отношении дорожно-строительной компании

Источник: составлено автором.

На гистограмме частоты первых двух цифр, Z-статистика которых превышает критическое значение, выделены желтым цветом, остальных – синим. Так, Z-статистики более половины объектов (58 из 90) оказались выше критических значений. Операции, начинающиеся с идентифицированных цифровых комбинаций, составляют 76% от общего объема транзакций, что в абсолютном выражении превышает 100 000 бухгалтерских записей. Столь значительный массив данных исключает возможность ручной верификации и требует применения дополнительных методов обработки, нивелируя потенциальный экономический эффект от закона Бенфорда.

Следующим важным недостатком является противоречивость результатов при применении различных методов проверки тесноты соответствия распределению Бенфорда. Так, статистика хи-квадрат характеризуется излишней категоричностью, часто указывая на несоответствие закону Бенфорда, даже в случаях, когда визуальное распределение выборки близко к теоретическому, а MAD подтверждает приемлемое соответствие. Данная особенность объясняется зависимостью статистики хи-квадрат от объема выборки, в то время как MAD такой зависимости не имеет. Кроме того, в большинстве случаев при анализе реальных наборов данных Z-статистики выходят за критические значения, противореча другим статистическим характеристикам.

При визуальном изучении гистограммы на рисунке 4 прослеживается общее соответствие распределению Бенфорда, несмотря на отдельные отклонения как в большую, так и в меньшую сторону. Данное наблюдение количественно подтверждается показателем MAD, составившим 0,0013. Согласно критериям, разработанным М. Нигрини и Н. Миттермайер, полученное значение MAD находится в интервале [0,0012; 0,0018], что указывает на приемлемое соответствие закону Бенфорда [18]. В то же время, другие статистические характеристики содержат противоположные выводы. Как описано выше, более половины всех рассчитанных Z-статистик оказались выше критического значения, что свидетельствует о несоответствии распределению Бенфорда и потенциальном искажении большей части данных. При этом тест реализован на крайне высокой доверительной вероятности – 99%. При ее снижении доверительный интервал будет сужаться, вследствие чего еще больше Z-статистик будет выходить за свои критические значения. Статистика хи-квадрат для этих же данных составила 1 885,69 при критическом значении 122,94, что также подтверждает несоответствие закону Бенфорда. Таким образом, статистические характеристики отражают взаимоисключающие результаты, что делает невозможным их обобщение или усреднение.

В ходе исследования также был выявлен ряд методологических проблем, связанных с критическими значениями статистических характеристик. Первая заключается в необходимости пересмотра критических значений Z-статистик, принимаемых в зарубежных работах как 1,96 для уровня значимости 5% и 2,57 для уровня значимости 1%. Эмпирические наблюдения показывают, что при анализе реальных данных, даже при их близком соответствии закону Бенфорда, происходит систематическое превышение установленных критических значений. Данное обстоятельство указывает на целесообразность корректировки данных пороговых значений в сторону увеличения. Вторая методологическая проблема касается интерпретации p-value в тесте суммирования, поскольку в практике данное значение практически всегда стремится к единице, создавая иллюзию соответствия закону Бенфорда. Третья проблема связана с отсутствием установленных критических значений показателя MAD для теста второго порядка, что существенно ограничивает возможности его практического применения.

Предлагаемым комплексным решением вышеуказанных недостатков является интеграция наиболее информативных статистических характеристик с последующим применением кластерного анализа. Данный подход обеспечит агрегированную оценку статистических характеристик, устраняя необходимость их индивидуального анализа и сопоставления. Кроме того, подход позволит сформировать кластер, состоящий только из наиболее подозрительных операций и, как следствие, имеющий небольшой объем, что сделает возможным его дальнейший ручной анализ.

Отдельного внимания заслуживает группа ограничений, связанная с затруднительностью внедрения рассматриваемых статистических методов в систему процедур диагностики недобросовестных действий в ходе аудита финансовой отчетности. Несмотря на установление МСА 240 рамочных требований к аудиторским процедурам в ответ на РСИНД, которые предоставляют аудиторам определенную гибкость в разработке собственных методологических подходов, любой подобный подход должен полностью соответствовать требованиям международных стандартов аудита.

Во-первых, в соответствии с МСА 500 «Аудиторские доказательства», при использовании информации, подготовленной организацией, аудитор должен провести оценку ее надежности. В частности, стандарт предписывает получение аудиторских доказательств относительно точности и полноты информации, а также оценки уместности и достаточности информации для целей аудита [6, п. 9]. В рамках текущего исследования такой информацией будет являться выгрузка журнала бухгалтерских записей из учетной системы. Прежде чем приступать к ее анализу по существу, аудитору необходимо верифицировать полноту, точность и надежность полученных данных. Данный аспект приобретает особую значимость в контексте выявления недобросовестных действий. Существует риск преднамеренной модификации выгрузки, предварительно исключив из нее операции с признаками мошенничества. В таком случае последующий анализ утратит свою результативность и практическую ценность для целей аудита.

Во-вторых, закон Бенфорда в его классической интерпретации представляет собой исключительно статистический инструментарий, анализирующий количественные закономерности в суммах операций. При его применении оказываются упущенными качественные индикаторы подозрительности, которые могут содержаться в иных параметрах бухгалтерских записей (счета учета, дата операции, аналитические признаки (субконто), подтверждающие документы, авторы проводки и другие). Подобные характерные черты умышленно искаженных бухгалтерских записей приводятся в МСА 240. В частности, подозрительными считаются записи, которые:

· выполнены по несвязанным, нетипичным или редко используемым счетам;

· внесены сотрудниками, в чьи стандартные обязанности не входит ведение бухгалтерского учета

· регистрируются в конце периода или по его завершении и имеют недостаточно пояснений;

· осуществлены непосредственно перед или в процессе формирования финансовой отчетности без надлежащего отражения в учетных регистрах, и др. [5, п. А43].

В-третьих, МСА 240 требует как первичной оценки РСИНД, так его последующей переоценки при обнаружении искажений, потенциально связанных с недобросовестными действиями. Проверка надлежащего характера бухгалтерских записей выступает в качестве ответной процедуры на первоначальную оценку РСИНД. По результатам процедуры важно верифицировать точность проведенной и убедиться, что она не оказалась заниженной. Несмотря на то, что повторная оценка РСИНД может осуществляться посредством различных процедур, включая применение профессионального суждения аудитора, количественная оценка представляется более объективным и надежным инструментом. В связи с этим целесообразно интегрировать её в разрабатываемую методологию в качестве как агрегирующего итога всего проведенного анализа. Эффективным решением для реализации данного подхода может служить применение теоремы условной вероятности Томаса Байеса, которая широко применяется как надежный инструмент принятия решений в условиях неопределенности.

Таким образом, в связи с выявленными ограничениями существующих подходов, включая недостаточную эффективность статистических методов на основе закона Бенфорда и их несоответствие требованиям международных стандартов аудита, разработана комплексная авторская методология, в схематичном виде представленная на рисунке 5.

Рисунок 4. Авторская методология интеграции закона Бенфорда в состав аудиторских процедур в ответ на РСИНД

Источник: составлено автором.

Предложенная методология предполагает поэтапную аналитическую обработку массива бухгалтерских проводок, экспортированных из учетной системы, в разрезе четырех компонентов – проверка популяции на надежность, тестирование законом Бенфорда, кластеризация и переоценка РСИНД. Результаты анализа консолидируются в файле формата *.xlsx (MS Excel), который выступает в качестве проформы рабочего документа аудитора.

В качестве подготовительного этапа требуется выгрузка учетных регистров из системы бухгалтерского учета за анализируемый временной интервал (как правило, отчетный год), а именно:

1. Журнал хозяйственных операций (журнал проводок), содержащий детализированную информацию о всех бухгалтерских записях;

2. Оборотно-сальдовая ведомость (ОСВ), представляющая собой сводный регистр бухгалтерского учета, отражающий остатки на начало и конец периода, а также дебетовые и кредитовые обороты по всем счетам за период.

Данные формы являются фундаментальной информационной базой для последующего анализа.

1. Проверка популяции на надежность

В целях соблюдения требований МСА 500 предусмотрен комплекс из трех последовательных тестов, направленных на оценку точности и надежности исходной популяции данных. Отрицательный результат хотя бы одного из тестов служит основанием для признания популяции ненадежной, что исключает возможность проведения дальнейшего тестирования.

1.1 Проверка целостности данных

Журнал операций необходимо проанализировать на предмет выявления бухгалтерских записей с отсутствующим счетом по дебету или кредиту. Исключение составляют забалансовые счета, которые по своему характеру содержат односторонние записи.

1.2 Проверка математической точности

Для каждого счета в оборотно-сальдовой ведомости следует проверить выполнение равенства: Сальдо начальное + Дебетовый оборот – Кредитовый оборот = Сальдо конечное. Наличие отклонений является свидетельством нарушений в формировании оборотно-сальдовой ведомости или ее намеренного искажения.

1.3 Проверка полноты выгрузки

В целях проверки сопоставимости выгруженных регистров необходимо сравнить суммарные обороты по каждому счету из журнала операций с соответствующими показателями оборотно-сальдовой ведомости. Выявленные несоответствия могут быть следствием как технических неточностей в процессе формирования и выгрузки регистров, так и недобросовестных действий.

2. Тестирование законом Бенфорда

В структуре предлагаемой методологии ключевое место занимает реализация системы тестов, основанных на законе Бенфорда, которая была подробно описана ранее и схематично проиллюстрирована на рисунке 3. Первоначальным этапом является выбор доверительной вероятности как в целях соблюдения баланса между уровнем уверенности и точностью выявления потенциальных искажений. Как правило, тесты выполняются на доверительной вероятности 95% или 99%. Процедура предполагает последовательное выполнение базовых, продвинутых и связанных тестов, что обеспечивает всесторонний характер исследования.

Каждый тест предполагает визуальное представление результатов в виде гистограмм, отражающих теоретическое и фактическое распределения, а также величину отклонений между ними. Визуальный анализ дополняется количественной оценкой статистических характеристик, включая расчет Z-статистики, статистики хи-квадрат и MAD, представленных ранее в таблице 2. Интеграция качественных и количественных методов анализа позволит сформировать комплексную систему индикаторов в целях дальнейшей идентификации операций, содержащих признаки недобросовестных действий.

3. Кластерный анализ

Кластерный анализ (кластеризация) представляет собой многомерный статистический метод, цель которого состоит в разбиении набора объектов на группы таким образом, чтобы профили объектов в одной и той же группе были максимально похожи друг на друга (внутренняя сплоченность кластера), а объекты разных кластеров, наоборот, различны (внешняя изоляция кластера) [8]. В рамках текущего исследования кластерный анализ позволит агрегировать статистические характеристики, полученные на предыдущем этапе. На основе данного признакового пространства станет возможным выделение класса наиболее подозрительных операций. Важным преимуществом алгоритмов кластеризации является их способность к автоматическому выявлению скрытых закономерностей в данных, что обеспечивает объективную группировку аномальных операций без необходимости явного задания правил классификации.

3.1 Выявление класса подозрительных операций

В состав признакового пространства целесообразно включить Z-статистику для различных видов тестирования (тест первой цифры, тест второй цифры, тест первого порядка, тест второго порядка, тест последних двух цифр), поскольку данный показатель выявляет отклонения на уровне конкретных операций, а не всей совокупности в целом. Кроме того, в отношении каждой операции возможно рассчитать частоту суммы по тесту суммирования и общую частотность по тесту дублирования. Таким образом, каждый объект будет характеризоваться, как минимум, семью признаками. Полученные данные структурируются в виде матрицы «объект-свойство» и подлежат стандартизации вследствие различных единиц измерения.

3.1.1 Определение оптимального числа классов

Прежде чем проводить кластеризацию, необходимо определить оптимальное число классов. Среди множества существующих методов (индексы Калински-Харабаза, Дуды-Харта, методы «каменистой осыпи» и «локтя») наиболее эффективным представляется метод силуэта, оценивающий качество кластеризации через сравнение схожести объекта в кластере относительно соседних. Поскольку значение силуэта может продолжать расти с увеличением числа кластеров, в данном исследовании их количество целесообразно ограничить диапазоном от 2 до 5, выбирая максимальное значение метрики среди первых четырех разбиений. Такое ограничение обусловлено необходимостью сохранения интерпретируемости результатов и предотвращения избыточной сегментации данных.

3.1.2 Выделение главных компонент

Для визуального анализа структуры данных рекомендуется применить метод главных компонент (Principal Component Analysis, PCA). Данный подход позволит осуществить снижение размерности признакового пространства до двух основных компонент, что даст возможность построить наглядную визуализацию распределения объектов в соответствии с предварительно определенными классами. Метод направлен на оценку формы и взаимного расположения кластеров, а также на идентификацию потенциальных выбросов и аномальных объектов в исследуемом наборе данных.

3.1.3 Проведение кластеризации методом k-средних

Для идентификации подозрительных операций применяется кластерный анализ методом k-средних. Выбор данного метода обусловлен его вычислительной эффективностью при обработке больших массивов данных и соответствием требованиям метрики силуэта для оптимального выделения кластеров с четкими границами. Анализ результатов кластеризации включает расчет количественных характеристик полученных классов, а также визуализацию средних значений признаков в каждом классе.

3.1.4 Выявление аномального класса

Практика демонстрирует, что применение исключительно кластерного анализа не обеспечивает достаточного сокращения объема данных для возможности дальнейшего ручного анализа. В связи с этим возникает необходимость в дополнительной обработке и сужении количества операций.

Для решения данной задачи предлагается использовать два взаимодополняющих метода обнаружения аномалий:

1. Изоляционный лес (Isolation Forest) – метод, который эффективно выявляет выбросы в сложной структуре данных с неявно разделяемыми группами аномалий. Применение метода в сочетании с кластеризацией позволит идентифицировать отдельные операции, характеризующиеся либо редкими значениями признаков, либо значительным отклонением от центроидов соответствующих кластеров.

2. Эллиптическая огибающая (Elliptic Envelope) – метод, основанный на предположении о близком к нормальному распределению данных внутри кластеров. Метод эффективно выявляет операции, выходящие за пределы ожидаемого распределения, что дополняет изоляционный лес.

Каждый из вышеуказанных алгоритмов (метод k-средних, изоляционный лес и эллиптическая огибающая) производит отдельную оценку аномальности операций. Затем для каждого метода определяется класс с максимальной концентрацией аномальных наблюдений. Итоговый класс подозрительных операций формируется путем пересечения множеств, обнаруженных всеми тремя методами. В исключительно редких ситуациях, когда алгоритмы идентифицируют различные классы как аномальные, производится не пересечение, а объединение классов. По итогам данного этапа формируется ограниченная выборка наиболее подозрительных операций, размер которой оптимален для последующего детального изучения вручную.

3.2 Группировка операций по подозрительным признакам

В целях соблюдения требований международных стандартов аудита необходимо дополнительно сгруппировать операции, вошедшие в сформированную выборку, на основе характерных признаков преднамеренно искаженных бухгалтерских записей согласно МСА 240. Анализ стандарта позволил выделить восемь индикаторов, которые возможно извлечь из содержания журнала операций, а именно частота дебетового и кредитового счета, частота проводки, частота автора операции, признак ручной проводки, признак сторнирования, проведение в нерабочее время, число дублирований (операций с идентичной корреспонденцией счетов и суммой).

Данная система индикаторов формирует признаковое пространство, используемое для последующей кластеризации методом k-средних, что методологически соотносится с предыдущим этапом исследования. Существенным отличием является целевая направленность кластеризации – если на предшествующем этапе метод применялся для идентификации единственного наиболее подозрительного класса с исключением остальных, то в рамках текущего этапа он используется для группировки операций по различным категориям подозрительных признаков. Вследствие этого отсутствует необходимость в применении методов выявления аномалий (ранее этап 3.1.4), поскольку все анализируемые операции уже характеризуются признаками потенциальных недобросовестных действий. Реализация данного этапа не только обеспечивает соблюдение требований МСА, но и способствует упрощению дальнейшего анализа операций.

4. Переоценка РСИНД

Заключительный этап аудиторской процедуры представляет собой переоценку РСИНД на основе интегрального индекса. Данная переоценка направлена на подтверждение или опровержении оценки РСИНД, которая предваряла детальное тестирование с помощью закона Бенфорда. Вопросы первоначальной оценки РСИНД не входят в объем настоящего исследования.

При формировании интегрального индекса целесообразно использовать ранее рассчитанные статистические характеристики. При этом следует включать метрики, характеризующие искажение выборки в целом, нежели чем оценивающие подозрительность отдельных операций (примененные при кластеризации). В качестве таких статистических характеристик предлагается использовать следующие среднее абсолютное отклонение (MAD) по тесту первой цифры, тесту второй цифры, тестам первого и второго порядка, а также коэффициент искажения, оцененный в рамках связанного теста под номером 2.3.3 (см. рисунок 5).

В качестве метода агрегирования данных показателей и последующего расчета РСИНД целесообразно использовать теорему Томаса Байеса, позволяющую вычислить апостериорную вероятность события на основе априорной вероятности и дополнительной информации по результатам проведенных тестов.

Математическая модель количественной оценки РСИНД с помощью теоремы Байеса может быть представлена следующим образом:

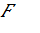
где:

· – апостериорная вероятность существенного искажения вследствие недобросовестных действий (пересмотренная оценка РСИНД);

· – априорная вероятность существенного искажения вследствие недобросовестных действий (первичная оценка РСИНД);

· – вероятность наличия индикаторов риска при существовании недобросовестных действий;

· – вероятность наличия индикаторов риска при отсутствии недобросовестных действий.

Полученный результат представляет собой вероятностную оценку в диапазоне от 0 до 1 (или от 0% до 100%), которая затем интерпретируется согласно установленной качественной шкале, например:

1. низкий уровень риска (0-20%);

2. уровень риска ниже среднего (20-40%);

3. средний уровень риска (40-60%);

4. уровень риска выше среднего (60-80%);

5. высокий уровень риска (80-100%).

Градация качественной шкалы может варьироваться в зависимости от принятой в аудиторской организации методологии.

Результаты проведенной аудиторской процедуры подлежат документированию в рабочем документе, который в соответствии с МСА 230 «Аудиторская документация» должен отражать характер, сроки и объем выполненных процедур, их результаты, собранные аудиторские доказательства и выводы [4, п. 8].

Заключение

В результате проведенного исследования установлено, что современный аудит демонстрирует существенные ограничения в области выявления недобросовестных действий, что не соответствует высоким ожиданиям пользователей финансовой отчетности и обуславливает необходимость совершенствования методологии аудиторских процедур. На основе систематизации российских и зарубежных научных работ выявлено, что закон Бенфорда представляет собой перспективный статистический инструментарий, имеющий потенциал применения в качестве аудиторской процедуры проверки надлежащего характера бухгалтерских записей. Вместе с тем, существующие подходы к его практической реализации характеризуются рядом методологических ограничений, включая неоднозначность интерпретации полученных результатов и недостаточную адаптацию к специфике аудиторской деятельности.

Предложенная в исследовании комплексная методология, основанная на интеграции закона Бенфорда с современными методами интеллектуального анализа данных, позволяет эффективно преодолевать выявленные недостатки. Практическая апробация разработанного подхода в условиях реальных аудиторских проверок демонстрирует его высокую результативность в выявлении признаков недобросовестных действий, при одновременном существенном снижении трудоемкости и упрощении процедур аудита. Полученные результаты свидетельствуют о перспективности дальнейшего развития и внедрения предложенной методологии в практику аудиторских организаций.

В качестве направлений дальнейших исследований следует отметить необходимость более широкой апробации предложенной методологии на предприятиях различных отраслей, масштабов и специфики деятельности. Кроме того, перспективным направлением является разработка программного обеспечения для полной автоматизации методологии, что позволит оптимизировать трудозатраты аудитора на техническую работу и сосредоточиться на содержательной части анализа.