Использование методов интеллектуального анализа данных для целей контроля

Введение

Актуальность темы. Современные условия характеризуются возрастанием рисков в сфере экономической безопасности, что обусловлено наложением ряда факторов: структурного экономического кризиса, последствий пандемии, общемировых рецессивных тенденций, проведением специальной военной операции, введением рестрикций со стороны недружественных государств и др. Все это приводит к нарастанию угроз устойчивому развитию отечественной экономики и стремлению хозяйствующих единиц избежать всеми возможными способами негативных последствий. В этой связи проблемы национальной экономической безопасности приобретают особую остроту. Анализ подходов к пониманию сущности экономической безопасности показал, что большинство трактовок данной дефиниции строятся на «учете и балансе интересов» [6]. Интересы государства в целях обеспечения экономической безопасности базируются на сохранении нации, целостности территории, обеспечении суверенитета, росте благосостояния населения, защите от враждебных воздействий, сохранении экологии, укреплении мировых позиций. [9] Немаловажное значение при обеспечении экономической безопасности уделяется технологическому суверенитету, обеспечивающему беспрепятственное использование в критически важных сферах экономики необходимых современных технологий [3]. Огромное внимание уделяется вопросам экономической безопасности на макроуровне [5, 7, 12, 15, 17]. Однако не меньший интерес и несомненное практическое значение имеют исследования экономической безопасности на микроуровне и методики ее оценивания. Стремительные изменения в техническом, технологическом, цифровом развитии генерирует новые, не имевшиеся ранее риски и угрозы. Они относятся к сложно идентифицируемым, остаются преимущественно не выявленными и в совокупности наносят ущерб всей макроэкономической системе. Согласно Глобальному обзору экономических преступлений 2020 [19], 28 процентов всех экономических преступлений составляют сознательные искажения – манипулирование данными финансового учета. Это требует выработки новых инструментов и методов их выявления. [8] В этой связи внедрение новых методик осуществления мониторинга и выявления рисков экономической безопасности отдельных субъектов хозяйствования с использованием цифровых средств становится особенно актуальным. [4,10,13]. Одним из эффективных способов выявления мошеннических действий и сомнительных операций является применение закона Бенфорда. [11,14,16,18]

Цель исследования – определить эффективность статистического инструмента выявления аномалий и оценки риска на основе анализа массива финансовых данных организации с использованием закона Бенфорда. В качестве источника информации для проведения анализа применяется сгенерированный программно синтетический датасет, содержащий данные журнала проводок для лизинговой компании, являющейся средней по отрасли.

Научная новизна исследования заключается в подтверждении приемлемости практического использования для целей финансового контроля, мониторинга и аудита статистического метода выявления аномалий для целей оценки риска экономической безопасности на основе закона Бенфорда.

Гипотеза: применение статистических методов выявления и оценки риска существенного искажения данных финансовой информации вследствие недобросовестных действий повысит эффективность контрольных процедур.

Материалы и методы исследования. В работе использовались современные достижения в сфере цифровизации методов контроля, теоретические и методологические изыскания отечественных и зарубежных авторов по вопросам экономической безопасности. Общенаучные методы, такие как абстрактно-логический, системного подхода, наблюдения, анализа и синтеза, сравнения, моделирования, графический метод и др., позволили отразить основные аспекты проведенного исследования. Применение статистических методов и средств автоматизации расчетов позволили выявить нестандартные элементы в выборке финансовых данных, свидетельствующие о наличии искажений, что подтверждает их целесообразность и повышает эффективность аудиторских процедур, внутреннего финансового контроля и проведения финансового мониторинга. С помощью скрипта, выполненного на языке Python, были проведены базовые, продвинутые и связанные тесты, позволяющие проверить естественный характер массива данных.

Результаты и их обсуждение. Недостоверное представление финансового положения компании вводит в заблуждение инвесторов и подрывает доверие к экономической системе в целом. Кроме того, менеджмент организации, опираясь на анализ искаженной информации, не может принимать адекватные стратегические и оперативные решения. В связи с этим возникает необходимость применения различных подходов к оценке качества финансовой отчетности с целью выявления фактов мошенничества. С помощью статистических методов сформированы выборки наиболее рискованных операций на основе журнала хозяйственных операций лизинговой организации.

В процессе достижения поставленной цели были решены следующие задачи:

- осуществлена первичная обработка данных, проверка соблюдения условий для анализа законом Бенфорда;

- проведены базовое, продвинутое и связанное тестирование, позволяющее проверить естественный характер массива данных;

- проанализированы полученные результаты.

Для оценки массива данных на возможность применения закона Бенфорда были проверены следующие условия:

- данные являются числовыми, а не категориальными;

- распределение стремится к экспоненциальному;

- данные случайны по своей природе;

- применяются одинаковые единицы измерения (рубли);

- нет заданных минимальных и максимальных значений;

- в наборе больше мелких наблюдений, чем крупных;

- значительная выборка данных (173 958 сумм хозяйственных операций).

Журнал операций соответствует соблюдению условий для анализа и возможности применения закона Бенфорда. Исходный датафрейм имеет необходимый размер. Малые выборки не могут воспроизвести ожидаемые частоты Бенфорда, что приводит к отклонениям от закона. Это требование соблюдено, так как в файле анализируется больше 100000 операций.

После проверки данных проводится базовое тестирование на соответствие распределению Бенфорда: тест первой цифры, тест второй цифры и тест первого порядка.

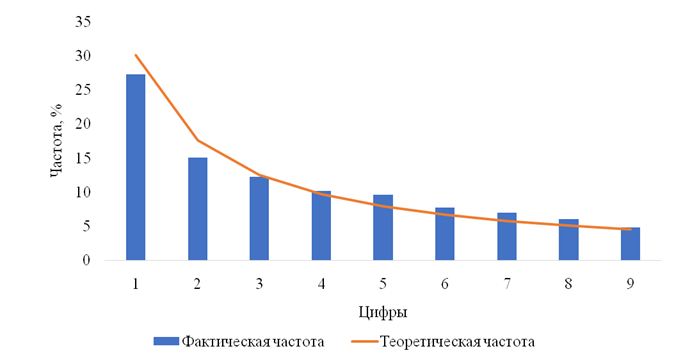
Рисунок 1. Теоретическое и фактическое распределение частот первых цифр

Источник: составлено авторами по исследуемым материалам организации.

Для тестирования первой цифры из массива данных по полю «Сумма» исключаются нематериальные значения (суммы меньше, чем 1 рубль), среди них отбирают первые цифры и строится гистограмма частот полученных значений, на нее наносятся линии ожидаемых частот (рис. 1).

Анализ строится на оценке показателей среднее абсолютное отклонение (𝑀𝐴𝐷) – для выборки; Z-статистика – для каждой цифры; статистика хи-квадрат – для выборки. По значениям Z-статистик можно сделать вывод, что для всех цифр присутствует риск манипулирования. Особенно существенно отличаются от ожидаемых частоты цифр 1, 2, 5, 7, поскольку их Z-статистики имеют наибольшие значения.

Таблица 1. Показатели соответствия выборки распределению Бенфорда для первых цифр

При проведении тестирования второй цифры по значениям Z-статистик сделан вывод о том, что компания не искажала значения сумм, вторые цифры которых это 6 и 8, поскольку их Z-статистики меньше критического значения. Для остальных цифр присутствует риск манипулирования, в особенности это касается цифр 0 и 5, поскольку их Z-статистики принимают наибольшие значения, а также наблюдается сильное отклонение фактической частоты от ожидаемой для этих цифр (рис. 2).

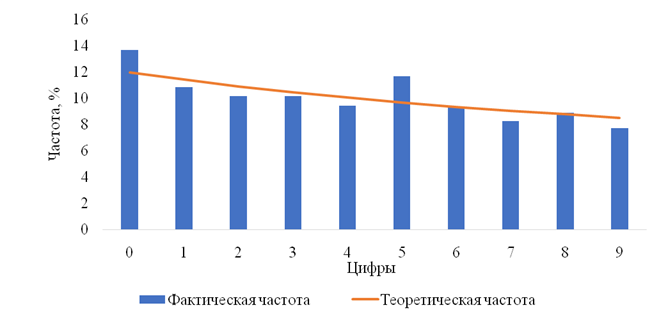
Рисунок 2. Теоретическое и фактическое распределение частот вторых цифр

Источник: составлено авторами по исследуемым материалам организации.

Тестирование первого порядка проводится исключением из анализируемого массива данных по полю «Сумма» значений меньше, чем 10 рублей, среди них отбирают первые две цифры и строится гистограмма частот полученных значений и линии ожидаемых частот. Согласно значениям Z-статистик, суммы, первые цифры которых это 25, 30 и 50, встречаются намного чаще, чем этого требует закон Бенфорда. Суммы, начинающиеся с цифр 17, 19, 21, 23, 24 встречаются значительно реже.

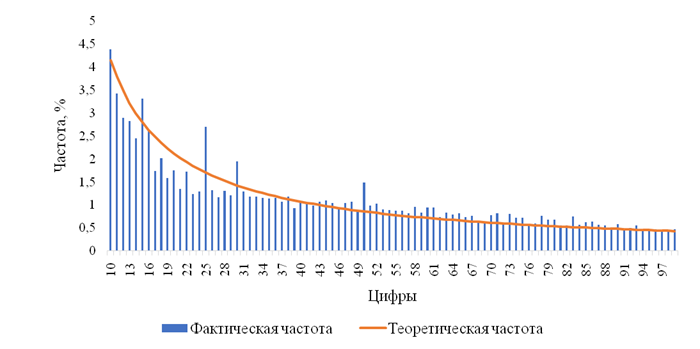
Рисунок 3. Теоретическое и фактическое распределение частот первых двух цифр

Источник: составлено авторами по исследуемым материалам организации.

На рис. 3 видно, что значения частот перед «пиковыми» частотами существенно меньше ожидаемых. Поэтому можно сделать вывод о том, что такое искажение вызвано округлением сумм операций в большую сторону, до числа, кратного 5.

После базовых тестов осуществляется проведение продвинутых тестов: тест суммирования, тест второго порядка и тест мантисс. Для проведения теста суммирования из массива данных по полю «Сумма» исключены значения, которые меньше, чем 10 рублей, среди них отбираются первые две цифры, рассчитываются суммы всех полученных элементов в разрезе первых двух цифр и строится гистограмма частот полученных значений по рассчитанным суммам, на нее наносится линию ожидаемой частоты (0,11).

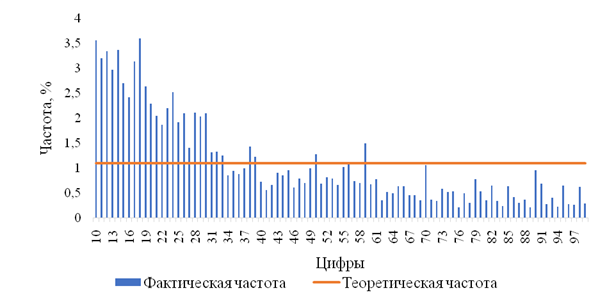
Рисунок 4. Теоретическое и фактическое распределение частот сумм

в разрезе первых двух цифр

Источник: составлено авторами по исследуемым материалам организации.

Если отсортировать исходный массив данных по убыванию значения поля «Сумма», можно убедиться, что самые крупные суммы действительно начинаются с цифр с наибольшими абсолютными отклонениями от средней частоты. Так, например, для цифры 19 это «Выдача кредита…» на сумму 196 278 801, 41 руб., для цифры 18 – «Корректировка выпуска продукции (услуг)» на сумму 184 758 275,19 руб., для цифры 17 – «Выдача кредита…» на сумму 170 000 000 руб. Согласно предусмотренным в МСА 240 «Обязанности аудитора в отношении недобросовестных действий при проведении аудита финансовой отчетности» признакам, корректирующие записи являются подозрительными и потенциально могут иметь мошенническую природу. В стандарте также указывается, что нетипично крупные суммы также являются подозрительными [1].

Для проведения теста мантисс рассчитаны x и y координаты мантисс логарифмов данных по полю «Сумма», а также x и y координаты центра тяжести. Согласно рис. 5, мантиссы логарифмов равномерно распределены по окружности, а центр тяжести близок к (0;0).

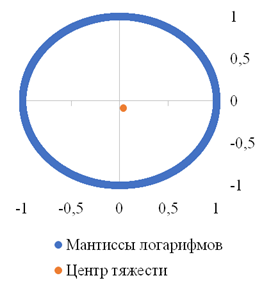
Рисунок 5. Дуговой тест мантисс

Источник: составлено авторами по исследуемым материалам организации.

Длина среднего вектора равна 0,008, а значение p-value равно 1, что больше критического значения, равного 0,05, и это говорит о том, что нулевая гипотеза о соответствии распределению Бенфорда подтверждается, можно сделать вывод, что в суммах бухгалтерских проводок содержатся данные, которые не искажают существенно показатели отчетности. По результатам проведенного анализа наиболее рискованные суммы операций приведены в таблице 2.

Таблица 2. Наиболее рискованные суммы операций

Выбор всех операций, отмеченных как подозрительные всеми тестами и имеющих признаки, указанные в таблице 2 позволяет сгруппировать их по содержанию (таблица 3). Содержание хозяйственной операции указано так, как в журнале операций проверяемой организации.

В качестве сомнительной операции была выделена «вычет НДС по предоплате» на сумму более 500 млн руб., эта операция действительно требует усиленной проверки (формальная проверка документов, проверка факта оплаты, правильности постановки объекта в бухгалтерском учете и др.), так как это связано с возвратом средств из бюджета и подвергается пристальному вниманию со стороны налоговой службы.

Начисление долга по страховым платежам является сомнительной операцией, так как не имеет экономического смысла, так как в журнале операций дебет и кредит синтетического счета и субсчета к нему для всех операций с таким содержанием одинаковы.

В качестве сомнительных операций были выделены операции с содержанием «начисление резерва по сомнительным долгам», что требует проверки правильности этой операции, а именно: порядок формирования резерва, предусмотренный учетной политикой предприятия, обоснованность отнесения задолженности к сомнительной по периоду просрочки. Также большая сумма свидетельствует о том, что работа с контрагентами ведется плохо: заключаются договоры с неплатежеспособными клиентами или сознательно допускающими просрочку.

Таблица 3. Наиболее рискованные категории операций (млн руб.)

В качестве подозрительных были отмечены операции «Восстановлены резервы по сомнительным долгам», что говорит о необходимости обратить внимание на методику расчета резерва сомнительных долгов. Этой операцией бухгалтер исправлял ошибку в неправильном начислении резерва. Однако такой метод исправления не считается корректным. Большое число операций с таким содержанием и существенность общей суммы этих операций (более 21 млн руб.) говорит либо о неправильной классификации задолженности, определении срока, применении методики расчета, либо организация сознательно увеличивает резервы по сомнительным долгам, чтобы уменьшить налог на прибыль.

Также подозрительными отмечены операции с содержанием «Передача основных средств». Среди этих операций содержатся как факты списания ранее используемых внутри организации объектов, так и передачи объектов, находящихся в лизинге. Нужно проверить законность списания основного средства. Если передается объект, бывший в лизинге, нужно проверить полноту получения за него лизинговых платежей.

Сомнительной операцией является «Оплата агентского вознаграждения по договору». Эта операция была проведена не один раз, а серией платежей с одинаковыми реквизитами по 500 тыс. руб. в течение одного дня по одному и тому же договору. Дробление сумм может свидетельствовать о том, что организация пыталась обойти Федеральный закон от 07.08.2001 №115-ФЗ «О противодействии легализации (отмыванию) доходов, полученных преступным путем, и финансированию терроризма» [1].

Заключение.

Применение математических методов позволяет повысить эффективность работы аудиторов, налоговых инспекторов, внутренних контролеров, освобождая от необходимости проверки рутинных фактов хозяйственной жизни, сужая объем работы и акцентируя внимание на операциях, требующих применения дополнительных процедур. Использование закона Бенфорда для обработки больших массивов учетных данных оказало высокую результативность. Выбранные после проведения тестов операции действительно можно отнести к сомнительным, а их суммы являются существенными. Полученные авторами результаты можно экстраполировать на другие организации различных отраслей экономики.