Моделирование роста народонаселения земли для прогнозирования экономики труда государства

Введение

Так как состояние развития общества в основном определяется уровнем инновационного внедрения технологий во всех научно-технических областях и зависит от множества общеэкономических, социально-культурных и военно-политических факторов общемирового и внутригосударственного значения, то особое значение для роста внутреннего валового продукта страны и экономики труда государства приобретает математическое моделирование и прогнозирование на несколько десятков лет вперед численности населения страны (НС) и народонаселения Земли (ННЗ).

Имея в достаточной степени точную математическую модель (ММ) роста ННЗ и результаты прогноза изменения НС, разрабатывается концепция увеличения населения РФ и как его наиболее эффективно использовать для роста благосостояния народа, экономического и оборонного могущества страны в перспективе. При этом, следует учитывать наличие тесных взаимосвязей между точностью полученной ММ роста ННЗ и прогнозами изменения НС с возможностью управляемой коррекции численности, а так же каким образом тенденция роста ННЗ и прогноз населения РФ могут оказывать влияние на развития всевозможных логистических систем (информационных, транспортных, производственных, складских и др.).

Проблема поиска наиболее подходящей ММ роста народонаселения на планете Земля решается исследователями несколько веков, однако до настоящего времени она решена только частично и с большими погрешностями для прошлых десятилетий, не говоря о низком качестве прогнозирования даже на несколько лет для будущих поколений. Что касается возможного соответствия имеющихся ММ роста ННЗ полученным официальным статистически данным [1], то эти ММ не отвечают действительности с большой погрешностью в границах ближайших нескольких лет хода истории.

Решение проблемы по разработке и проверке на точность любой ММ для учета роста ННЗ усугубляется трудностью получения точных исходных данных для проверки предлагаемой модели на адекватность, так как в большинстве случаев наблюдаются следующие недостатки по сбору статистических данных:

перепись населения производится в каждой из большого числа стран не в один и тот же год (не одновременно), а также с разной погрешностью по объективным причинам (например, отсутствие возможностей или средств) и субъективным причинам (например, приписывание численности населения для получения помощи от международных организаций);

количество населения во многих странах рассчитывается путем использования предшествующих последних данных переписи и после приблизительного определения роста населения в день производится умножение на число дней для заданного периода времени;

в результате суммирования полученных данных по всем странам Земли получают общий результат, который представляется наглядно в виде счетчика населения Земли с периодом обновления вплоть до секунды, но не гарантирует реальную точность даже в несколько процентов.

Тренды и ритмы в эволюции цивилизации в целом и роста ННЗ в частности могут быть описаны и зачастую описываются различными уравнениями (линейными, нелинейными, логарифмическими, степенными и др.), а их типы устанавливаются путем подбора соответствующей тренду или ритму функциональной модели статистическими методами (параметрическими) либо методами сглаживания исходного временного ряда (непараметрическими).

Опираясь на анализ тренда роста ННЗ за последние примерно четверть века и полученные автором ММ для определения периода жизненного цикла цивилизации и тенденции изменения численности населения на нашей планете [2], произведем уточнение этой модели.

Требования к математическим моделям народонаселения Земли и условия их реализуемости

Степень эволюции общества с учетом влияния искусственных факторов развития в основном зависит от роста расходования материальных ресурсов, развитости транспортных, инфокоммуникационных и логистических систем, где особое и резко прогрессирующее в развитие место приобретает информационная составляющая. То есть, на рост ННЗ в предыдущие несколько столетий наряду с увеличением использования полезных материальных ресурсов и вырабатываемых разновидностей энергии (электрической, ядерной и др.) стала оказывать существенное влияние всеобщая информатизация с последующей цифровизацией, для которых характерно преобладание искусственных производительных сил над естественными с массовым внедрение искусственного интеллекта во все сферы жизнедеятельности общества (экономическая, политическая, социальная, духовная).

В обобщенном виде тенденцию роста ННЗ предлагается представлять, как зависимость от технологического прогресса, который базируется не только на росте потребления материальных и энергетических ресурсов, но в основном зависит от увеличения объемов обмена информационным ресурсом, а также от объемов его обработки и хранением с целью развития инфокоммуникационных систем для внедрения более перспективных технологий во все области жизнедеятельности человечества и конкретной личности. Эту тенденцию роста ННЗ следует не только увязывать с генетическим информационным кодом (биологическим фактором), но также следует увязывать в комплексе с технологическим прогрессом и ростом влияния информационных процессов на развитие технологических процессов в условиях не уменьшения потребления материальных и энергетических ресурсов. Следовательно, с учетом изложенного обоснования, наряду с общепринятым понятием «век» в 100 лет введем понятие «информационно-технологический век» (ИТВ), шкала которого «сжимается» по закону геометрической прогрессии (ГП) и будет отличаться от равномерной шкалы, а также будет принимать значения в зависимости от степени инфотехнологического развития общества (социально-экономического фактора) и биологического фактора на генетическом уровне, как некого информационно-технологического комплекса в развитии цивилизации.

Анализ множества подходов к математическому моделированию ННЗ показал, что к их содержанию чаще всего предъявляются следующие требования и условия реализуемости [1, 3]:

историческая шкала времени должна быть обосновано привязана к демографической шкале ННЗ, а погрешность ММ по отношению к статистическим данным не должна превышать ;

описание роста ННЗ должна охватывать тысячи лет с приоритетом более точного учета численности населения в точках официально полученных статистических данных в течение сотен лет;

основным подходом к разработке ММ для ННЗ является макроописание, существо которого заключается в учете при необходимости исключительно существенных деталей демографического процесса с учетом изменения соотношений между ростом потребления человечеством материальных, энергетических и информационных ресурсов;

модель должна отражать циклическую динамику роста населения и может состоять из нескольких уравнений, число которых должно быть минимизировано;

введение очередного уравнения в ММ должно быть строго обосновано, например, после окончательного формирования социальной среды обитания в человеческом обществе применение известной популяционной модели Лотки-Вольтерра «хищник-жертва» стало не целесообразным из-за отсутствия ее адекватности при описании реальных демографических процессов, что привело к необходимости поиска более сложной модели с несколькими уравнениями;

эволюция народонаселения во времени не может быть монотонной и может рассматриваться в виде апериодических колебаний колебательного контура (осциллятора), периоды колебаний которого не повторяются через равные промежутки времени, но могут быть описаны математически, например, в виде ГП [2] или гиперболического роста [3];

изначально динамика популяции должна начинаться из двух особей и очень медленно расти, но на определенном этапе жизненного цикла темп роста должен существенно ускоряться, переходя к замедлению с предельным количественным значением численности населения Земли на завершающем цикле развития цивилизации;

учет изначально двух особей разного пола с дальнейшим увеличением популяции на их основе до некоторого количества, которое с научных позиций подлежит обоснованию, не следует рассматривать буквально в абсолютном исчислении, а может быть рассмотрено на генетическом уровне (ГУ) и инфотехнологическом уровне (ИТУ) развития популяций без подсчета человекоподобных особей древних периодов формирования человека-разумного, т. к. ГУ в этом древнем периоде доминировал над ИТУ;

математическая модель развития цивилизации (РЦ) во времени должна иметь сходство с ММ для ННЗ, а также сопрягаться в начальных и конечных точках завершения их функционирования в процессе проведения расчетов;

в математических моделях для РЦ и роста ННЗ должно быть предусмотрено получение промежуточные расчетов годов на шкале времени и численности населения по шкале народонаселения для полученных после расчета годов, в случаях, когда известны два ранее рассчитанные ближайшие к расчетному значению результаты.

Исследования показали, что приведенные выше требования и условия реализуемости для известного множества подходов к математическому моделированию ННЗ мало эффективно без применения наиболее адекватно подходящей ММ периодизации истории человечества (ПИЧ) [2], на анализе которой остановимся более подробно.

Математическая модель периодизации истории человечества на основе золотой геометрической прогрессии

В работе [2] автором приводятся результаты применения теории нечетких множеств для формализация множества наиболее важных событий мировой истории начиная с IV тысячелетия до н. э. и до 1995 г. (всего 800 событий), а также множества наиболее важных для развития общества научных открытий до 1986 г. (всего 80), где каждому историческому событию или научному открытию присвоена лингвистическая переменная с привязкой к оси времени в годах. На основе модифицированного метода статистического оценивания произведено многократное группирование спроецированных на ось времени наиболее важных событий (исторических и информационных в виде научных открытий), а обработка и анализ полученных результатов позволили получить ММ для расчета исторических периодов (ИП) ПИЧ в виде «золотой» ГП [2]

(1)

где: Ф = 1,618 033 988… – золотая пропорция (сечение), как знаменатель золотой ГП; 10³ – коэффициент масштабирования; n= 16,…,1, 0, –1,…,–16 – номера членов ГП, соответствующие номерам ИП, т. е. ИТВ на ИТУ развития в рамках ПИЧ. Результаты расчетов с помощью выражения (1) при n=16,…,1, 0 приведены в табл. 1, а при n = 0, –1,…,–16 – в табл. 2.

Таблица 1 – Результаты расчетов с помощью выражения (1) при n=16,…,1, 0

Таблица 2 – Результаты расчетов с помощью выражения (1) при n = 0, –1,…,–16

Анализ полученных результатов расчета в табл. 1 и табл. 2 показал:

ограничение в (1) максимальным положительным значением степени n=16 (это период, когда обитали в Эфиопии ардипитеки радимус и кадабба) обосновано тем, что три усеченные последовательности Фибоначчи чисел, как составляющие численных значений ИП I(n=8),…,I(n=16), теряют связь с тремя последовательностями Фибоначчи при n=17 (граница начала обитания ардипитека кадабба, датируемая 5,77 миллионов лет тому назад, которые примерно соответствуют граничному значению 5775882 г. до н. э. при n= 16);

переход от суммы трех последовательностей Фибоначчи к сумме двух усеченных последовательностей Фибоначчи чисел, как составляющих численных значений ИП I(n=7),…,I(n=0), при n=7, может характеризовать качественный переход для этого ИП I(n=7)=29 034 лет в границах 44 861 г. до н. э.– 73 895 г. до н. э. (период обитания неандертальцев);

ограничение в (1) максимальным отрицательным значением степени n=–16 обосновано тем, что для этой степени округление значений I(n=–16)=0, то есть полностью исчезает последняя из изначальных усеченная последовательность Фибоначчи, а сумма чисел обнуляется в 2118 году завершая описание этой математической моделью ПИЧ;

переход от двух последовательностей Фибоначчи к одной последовательности происходит при n=–7, что соответствуют граничному значению 2028 г. н. э.

Если совместить табл. 1 с табл. 2 при n=0, то сможем наблюдать закономерность последовательного сжатия ИП (ИТВ) по закону «золотой» ГП (1), начиная от I(n=16)=2 207 000 лет и завершая – когда I(n=–16)=0 лет в 2118 г. н. э.

Математические модели народонаселения Земли на основе золотых геометрических прогрессий

Не смотря на наличие не оправдавших себя в применении на практике прогнозирования роста населения множества подходов к разработке соответствующих ММ, в основу которых заложены разнообразные законы (удвоения, асимптотический, логистический, параболический, гиперболических и др.) [1;3–5], в ряде случаев исследователями уделялось внимание применению закону ГП с неизменными и меняющимися коэффициентами роста при экстраполяции, но ни один из них на практике не оправдался.

Анализ закона гиперболического роста ННЗ показал, что он позволяет производить оценки примерно с 1650 года по 1970 год, а до 1650 года и после 1970 года динамика численности населения подчиняется другим законам [3]. Например, не выдерживает критики гиперболический закон роста населения выдающегося астронома И. С. Шкловского [6], недостатки которого подробно раскрыты Б. Ц. Урланисом [4].

Известный ученый В. И. Вернадский отмечал, что уже в XVIII веке натуралисты установили факт размножения по закону ГП [7]. Учитывая этот факт и возможность формирования ИТВ в соответствии с ММ (1), сделаем предположение, что закон роста ННЗ не должен противоречить убывающей «золотой» ГП (1) для ПИЧ и должен иметь более точное выражение количества населения в виде возрастающей «золотой» ГП с возможностью перехода к дугой закономерности в точке качественного перехода («перегиба») при n=–7, что соответствует началу граничного значения 2028 г. н. э. Следовательно, для получения более точной ММ роста ННЗ произведем разбиение каждого из ИП шкалы роста населения с привязкой к летоисчислению в среднегеометрическом отношении с учетом выполнения характеристического свойства ГП. Для этого применим метод динамической аналогии по определению резонансной частоты («резонанса») осциллятора с позиции теории линейных электрических цепей и теории фильтрации сигналов электросвязи, когда известны нижняя (меньшая) и верхняя (большая) по величине частота полосы пропускания. То есть, произведем расчеты «резонансных» лет ( ), как среднегеометрических (СГ) значений ( ), для каждого ИП из табл. 1 и табл. 2 c учетом меньшего ( ) и большего ( ) граничных значений, что позволит получить в каждом из них по две неравномерных по значению полосы (полупериодов) в годах с помощью следующего выражения:

(2)

В результате применения выражения (2) к граничным значениям ИП, которые приведены в четвертой колонке табл. 1 и табл. 2, получим уточненную шкалу хронологической периодизации с годами в точках «резонанса» для каждого из ИТВ. Однако, для привязки этой шкалы к шкале роста ННЗ следует определиться с соответствующей ММ этого роста и возможностью получения после расчета первых двух человек. Для расчета роста ННЗ в работе [2] приведена ММ на основе золотой ГП:

(3)

Условием для совмещения (привязки) между собой временной шкалы ПИЧ (1) с шкалой роста ННЗ (3) является изначальное определение 2 человек, для чего подставим в (3) значение m = 46 применительно к начальному номеру ИП n = 16 и получим для 5 775 882 г. до н. э.:

(4)

Взяв за начало отсчета m=46 и n=16, а также учитывая (4) и рассчитанные среднегеометрические («резонансные») значения годов по формуле (2), производится распределение всех m=46,…,1 применительно к n= 16,…,1,0,–1,…,–6, где n=–6 является граничным из-за наличия в ММ для ПИЧ (1) качественного перехода от двух усеченных последовательностей Фибоначчи к одной последовательности при n=–7. Для примера в табл. 3 приведены результаты такого распределения при m=12,…,1 применительно к n= –1,…,–6, а также результаты расчетов по формуле (2) при n= –7…,–14, с хронологией привязки в годах нашей эры в соответствии с табл. 2.

Таблица 3 – Результаты расчетов с помощью выражения (2) при m=12,…,1 и n= –1,…,–6, а также при n= –7…,–14

После обеспечения взаимной привязки между (1) и (3) с помощью (4) для определения первых двух человек и распределения всех m=46,…,1 применительно к n= 16,…,1,0,–1,…,–6 с хронологической привязкой к годам в рамках всей ПИЧ, производится расчет численности ННЗ для полученных годов в рамках каждого из ИП (ИТВ). В табл. 4 приведены результаты расчетов численности ННЗ для полученных годов в рамках каждого из полупериодов ИП (ИТВ) применительно к данным в табл. 3, но в пределах применения выражения (3) при I(n)=–1,…,–6.

Таблица 4 – Результаты расчетов численности ННЗ для годов из табл. 3 при I(n)=–1,…,–6

Для проверки степени адекватности полученных результатов в табл. 4 представляет наибольший интерес ближайший и последний для полученной ММ 2000 год, так как для него известна примерная численность населения 0,6×10¹⁰ человек, которая с допустимой погрешностью –2,9 % соответствует «золотому» сечению человек. Расчет прироста населения (ПН) для каждого полупериода в рамках ИП выражается через разницу между граничными значениями численности ННЗ, а сами результаты расчетов в качестве примера с использованием данных из табл. 4 (с 1118 г. по 2000 г.) сведены в табл. 5.

Таблица 5 – Результаты расчетов ПН с использованием данных по ННЗ из табл. 4

Анализ данных из табл. 5 по ПН за полупериод с 1972 г. по 2000 г. млрд. чел.) и имеющейся по данным ООН статистики ННЗ до 2024 г. показывает, что в полупериоде с 2000 г. по 2028 г. динамика роста ННЗ может быть не только сохранена, но и распространится на следующий в исторической хронологии полупериод с 2028 г. по 2045 г., а тренд дальнейшего роста может моделироваться по следующему закону:

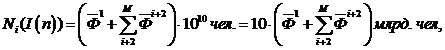(5)

где i = 1,…,M – порядковый номер полупериода в n-ом ИП (ИТВ) начиная с i = 1, берущему начало отсчета ПН с привязкой к 2000 г. при числе рассчитанного ННЗ по формуле (4), когда

В табл. 6 приведены результаты расчетов прогнозируемого роста ННЗ по формуле (5).

Таблица 6 – Результаты расчетов прогнозируемого роста ННЗ по формуле (5)

Сравнительный анализ данных ООН с результатами расчета на основе предлагаемых математических моделей народонаселения Земли

Анализ данных ООН по росту народонаселения Земли позволил выделить из них вековые реперные точки (года), которые привязаны к численности населения с равномерной шкалой от 1-го до 8-ми млрд. чел. [8; 9]: 1 млрд. чел. – 1800 г.; 2 млрд. чел. – 1927 г.; 3 млрд. чел. – 1960 г.; 4 млрд. чел. – 1974 г.; 5 млрд. чел. – 1987 г.; 6 млрд. чел. – декабрь 1999 г.; 7 млрд. чел. – 2011 г.; 8 млрд. чел. – ноябрь 2022 г.

Для ИП при n=–5,…,–13 присуща закономерность, когда СГ значения годов (2) с точностью до шести месяцем соответствуют среднеарифметическим (СА) результатам расчета для меньшего и большего граничных значений, т. е.

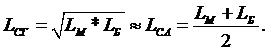(6)

Наличие закономерности (6) применительно к ИП в диапазоне лет от 1882 г. по 2115 г. позволяет вводить для каждого из ИП при n=–5,…,–13 равномерную шкалу с годичным ПН, путем умножения этого годичного приращения на конкретный номер по счету интересующего по народонаселению года в рамках исследуемого ИП.

Например, для ИП при n=–6 с хронологической привязкой (см. табл. 2) =1972 г. и =2028 г. произведем расчет с использованием выражения (6) и получим: Условие примерного равенства СГ и СА значений для данного ИП является необходимым для построения равномерной шкалы времени для диапазона в лет. Зная число населения в 2028 г. и в 1972 г. вычисляем ПН, как разницу, затем полученное значение ПН делим на 56 и получаем среднегодовой прирост ННЗ, который умножается на одно из чисел последовательности 2,…,55 с последующей привязкой к конкретному хронологическому году этого ИП при n=–6 .

Из приведенных выше реперных годов с привязкой к целочисленному значению ННЗ в млрд. чел. особое доверительное внимание привлекают годы, начиная с семидесятых годов, т. к. для этого периода времени (примерно равного пять десятилетий) статистические данные по народонаселению наиболее достоверные в сравнении с более ранними ИП.

В табл. 7 приведены статистические данные по ННЗ с учетом привязки конкретных годов к целочисленному значению ННЗ в млрд. чел., а также расчетные значения ННЗ по формуле (3) и пересчитанные значения численности населения применительно к годам в формуле (6) с привязкой к целочисленным статистическим данным от ООН.

Таблица 7 – Данные по ННЗ с учетом привязки годов к целочисленному значению, а также расчетные значения населения по формуле (3) и годов по формуле (6)

Анализ данных из табл. 7 показал:

до 1972 г. отклонения между расчетными значениями по формулам (3) и (6) в сравнении с приведенными по линии ООН, но которые невозможно отнести по объективным причинам получения к достоверным, превышают десять процентов;

после 1972 г. и по настоящее время (2024 г.) предложенные ММ в виде формул (3) и (6) позволили получить значения ННЗ с точностью, которая находится в пределах от +1,47% до -0,6% и соответствует допустимому отклонению не превышая .

Что касается результатам расчетов прогнозируемого роста ННЗ по формулам (3) и (6), которые приведены в табл. 6 и табл. 7, то они имеют теоретически обоснованный предел роста ННЗ по закону суммы обратного значения золотого сечения с золотой ГП: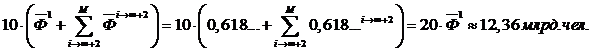

Из полученного нами по формуле (6) 2101года расчет ННЗ по формуле (3) составит 12,229 млрд. чел. (табл. 6, при I(n)=-10 и i =8), а после перерасчета на 2100 г. с учетом условия (3) и (6) получаем примерно 12,2 млрд. чел.

Оказывается, что наш прогноз ННЗ не противоречит прогнозу Центрального экономико-математического института Российской академии наук (ЦЭМИ РАН), что подтверждается полученными этим институтом следующими результатами научных исследований: «Наши прогнозы в общих чертах повторяют расчеты ООН, IIASA и IHME. Всего в мире к 2100 году будут жить 11773 млн человек, то есть почти 12 млрд. чел.» [8]. Если ЦЭМИ РАН допускает округление 11,773 млрд. чел. до 12 млрд. чел. в сторону увеличения численности ННЗ с точностью до +1,86%, то мы поступим таким же образом и округлим полученное значений 12,2 млрд. чел. до 12 млрд. чел. в сторону уменьшения численности ННЗ с точностью до -1,64%. Следовательно, в плане прогноза роста ННЗ к 2100 г. полученные нами результаты имеют допустимую погрешность, а совокупность ММ (1),…,(6) может использоваться научными организациями в качестве альтернативных.

Заключение

После обоснования требований к математическим моделям народонаселения Земли и представления разработанной ММ исторической периодизации истории человечества с учетом введения уменьшаемых по закону золотой ГП (1) ИТВ в настоящей научной приводятся две взаимно согласованные математические закономерностями (ММ) в золотых ГП, одна из которых – для расчета роста ННЗ в прошлом (3) до получения условных двух человек (4), а другая – для прогноза роста ННЗ в будущем (5) примерно до 2115 г. Прогнозы роста ННЗ к 2100 г., полученные нами и ЦЭМИ РАН имеют допустимую погрешность и могут использоваться научными организациями в качестве альтернативных при прогнозировании экономики труда государства.

Математическая модель (1) позволяет произвести расчет год (5 775 882 г. д. н. э.) с условным появлением на свет первых двух человек (4). Модель (3) позволяет получить значения ННЗ для нашего реально проживаемого времени в рамках имеющего конкретные статистические данные по линии ООН периода в 6-ть десятилетий (от 1972 г. и по 2024 г.) с высокой точностью в пределах от +1,47% до -0,6%. Что касается прогноза на будущее роста ННЗ, то результаты расчетов по формуле (5), которые приведены в табл. 6, позволили получить теоретически обоснованный предел роста ННЗ на 2115 год, а сама закономерность находится в согласованности с малой погрешностью относительно данных ООН для периода от 1972 г. по 2024 г.

Таким образом, имея в достаточной степени точную совокупность математических моделей (1),…,(6) с результатами прогнозируемого роста ННЗ (табл. 6) до 2115 г., предлагается разработать концепцию увеличения населения РФ и как ее наиболее эффективно использовать для роста благосостояния народа, экономического и оборонного могущества в перспективе на несколько десятилетий. При этом, следует учитывать наличие тесных взаимосвязей между точностью полученной ММ роста ННЗ и прогнозами изменения НС с возможностью управляемой коррекции численности, а так же каким образом тенденция роста ННЗ и прогноз населения РФ с учетом этой тенденции могут оказывать влияние на развития и внедрение перспективных инфокоммуникационных технологий, логистических систем и экономического развития государства.