Оценка влияния «зеленых» инвестиций в странах Евразийского экономического союза на величину загрязняющих атмосферу выбросов

Актуальность

Несмотря на непродолжительный срок существования ЕАЭС его участники активно включились в экологическую повестку, актуальную для всех современных экономик. Подтверждением этому служат как программные документы Евразийского экономического союза, так и опубликованные недавно соответствующие статистические данные, свидетельствующие о снижении выбросов СО2 в атмосферу в указанных государствах, а также о росте текущих затрат на охрану окружающей среды [1; 2; 3].

Литературный обзор

Как мы отметили выше, данная проблематика актуальна для подавляющего большинства современных стран, что подтверждается ростом числа публикаций на этот счет. Среди них наиболее релевантными целям нашего исследования нам показались следующие, связанные с «зеленым» финансированием:

- статья Дж. Янга [7]: Климатическое финансирование – это финансовое решение, которое появилось для решения проблемы изменения климата и развития низкоуглеродной экономики, и является важной тенденцией в развитии современных финансов. В статье в основном рассматриваются вопросы, связанные с климатическим финансированием. Исследования показали, что с глобальной точки зрения климатическое финансирование возникло с появлением проблем глобального изменения климата и неизбежно будет развиваться по мере углубления глобальных усилий по решению проблемы изменения климата. Смягчение последствий изменения климата, адаптация и коммерциализация экологически чистых технологий станут тремя основными направлениями поддержки климатического финансирования. Финансово-экологическая среда и ее различные факторы в пекинском районе Тяньцзинь Хэбэй, на примере которой написана статья, в целом положительно влияют на экономическое развитие, но влияние каждого фактора различается. Финансово-экологическая среда оказывает положительное стимулирующее влияние на рост экономических агрегатов и урбанизации.

- статья Ц. Лана, Х. Чена и др. [5]: чтобы достичь «углеродной нейтральности» в соответствии с утвержденным в КНР графиком, сфера услуг Китая должна добиться активизации «зеленого» развития. В статье авторы использовали интеграционную модель SBM-DDF для измерения экологической эффективности сферы услуг в 30 провинциях Китая в период с 2011 по 2019 год. На основе уровня «зеленой» эффективности сферы услуг Лан, Чен и др. использовали коэффициент Дагума-Джини и пространственную цепь Маркова для анализа источника регионального разрыва и пространственной динамической эволюции «зеленой» эффективности сферы услуг в четырех основных регионах Китая. Результаты показывают, что общая экологичность китайской сферы услуг растет, и между регионами существует значительная неоднородность; «зеленая» эффективность индустрии услуг Китая имеет очевидные характеристики пространственной дифференциации. Региональная дифференциация является основным источником его пространственной дифференциации, а вклад сверхплотности населения является наименьшим, что противоречит распространенным представлениям на этот счет. Провинции с высокой эффективностью сферы услуг в Китае оказывают положительное влияние на «зеленую» эффективность сферы услуг в соседних провинциях, в то время как провинции с низким уровнем эффективности будут оказывать определенное тормозящее влияние на «зеленую» эффективность сферы услуг в соседних провинциях.

- статья П. Жао, Ц. Лю и др. [10]: «зеленые» инновации способствуют качественному экономическому развитию и эффективной защите окружающей среды. В данной статья модель минимального расстояния до сильного эффективного рубежа (MinDS) использовалась для измерения эффективности «зеленых» инноваций 30 китайских провинций за период с 2000 по 2020 гг. Методы декомпозиции коэффициента Джини и оценки плотности ядра использовались для анализа региональных различий эффективности «зеленых» инноваций. Пространственная корреляция была оценена для анализа пространственных побочных эффектов и пространственной конвергенции эффективности «зеленых» инноваций. Названная эффективность Китая демонстрирует тенденцию к увеличению со значительными пространственными различиями между провинциями. Региональные различия и интенсивность трансвариации являются основными источниками пространственных различий в эффективности «зеленых» инноваций. Региональные различия в них уменьшились в наблюдаемый период за исключением восточных регионов страны. Результаты оценки пространственной сходимости свидетельствуют о пространственной абсолютной и условной сходимости во всех регионах. Следовательно, по мнению авторов статьи для повышения эффективности «зеленых» инноваций в Китае необходимо учитывать влияние экономического уровня, структуры промышленности и экологических норм.

- статья В. Ванга, В. Лю и др. [8]: в этом исследовании анализируются компании химической промышленности КНР с расходами на охрану окружающей среды, чтобы определить, какие из них имеют лучшие финансовые показатели. Кроме того, в этом исследовании используется анализ охвата данных для оценки эффективности фирм с расходами на охрану окружающей среды и без них. В этом исследовании также используется индекс производительности Малмквиста (MPI) для анализа изменения производительности фирм и метод начальной загрузки для проверки того, являются ли индексы статистически значимыми. Наконец, это исследование делит компании химической промышленности на три основные категории в зависимости от их продукции. Результаты этого исследования предоставляют убедительные доказательства взаимосвязи между расходами на охрану окружающей среды и финансовыми показателями. Полученные данные свидетельствуют о том, что фирмы с расходами на охрану окружающей среды имеют более высокую эффективность и производительность. Следовательно, исследование побуждает компании в отрасли прилагать больше усилий для защиты окружающей среды, что может быть достигнуто за счет более чистого производства для получения более высоких выгод.

- статья А. Баррелла, П. Добржански и др. [4]: как отмечают атворы статьи, политика охраны окружающей среды широко обсуждается в научных трудах. Однако особое внимание следует уделить и эффективности расходов на охрану окружающей среды, что и является основной целью названной работы. Страны Европейского союза были выбраны для данного анализа в связи с тем, что в последние годы этот регион стал неформальным мировым лидером в отношении реализации мер политики в области охраны окружающей среды. По этой причине использовалась методология анализа охвата данных, позволяющая рассчитать межотраслевую эффективность за 2005-2015 годы. Анализ показывает, что среди 30 проанализированных стран наиболее эффективной в природоохранной деятельности является Финляндия. Гипотеза о том, что более высокие расходы на охрану окружающей среды не приводят к улучшению экологических результатов, подтвердилась. Эти результаты аналогичны тем, к которым мы пришли в нашем исследовании. Анализ подтвердил проблему снижения эффективности расходов на охрану окружающей среды в выбранных странах-членах Европейского Союза.

- статья Ц. Ционга, Ю. Ванга и др. [9]: статья исследует влияние «зеленого» финансирования на оптимизацию промышленной структуры в Китае. Используя панельные данные 30 провинций за период с 2012 по 2020 год, авторы применяют метод взвешенного анализа TOPSIS для измерения уровня развития «зеленого» финансирования и уровня оптимизации промышленной структуры в Китае. В итоге исследования выявляется неравномерность и недостаточность развития зеленого финансирования и оптимизации промышленной структуры в стране. При этом обнаруживается значительное влияние «зеленого» финансирования на рационализацию и повышение качества промышленной структуры. Также отмечается различие в влиянии «зеленого» финансирования на оптимизацию промышленной структуры в разных регионах Китая и в различных отраслях. В итоге авторы предлагают рекомендации для государства и финансовых учреждений по использованию «зеленого» финансирования для поддержки оптимизации промышленной структуры Китайской народной республики.

Научный пробел

В научных исследованиях, связанных с влиянием инвестиций в природоохранные мероприятия на величину выбросов СО2, существуют следующий научный пробел:

1. Недостаток эмпирических исследований: существует потребность в большем количестве эмпирических исследований, которые бы обратились к реальным данным об инвестициях в природоохранные мероприятия и их влиянии на уровень выбросов СО2. Большинство существующих исследований в данной области являются модельными и теоретическими, в то время как недостаточно исследований, основанных на фактических данных и реальных мерах по сокращению выбросов углекислого газа.

2. Ограниченные данные и измерения: доступ к подробным данным об инвестициях в природоохранные мероприятия и их воздействию на выбросы СО2 является ограниченным. Существует необходимость в сборе и использовании более точных и надежных данных для понимания связи между инвестициями и выбросами СО2.

Все это указывает на необходимость дальнейших исследований в данной области, чтобы более точно понять и доказать влияние инвестиций в природоохранные мероприятия на снижение выбросов СО2 и способствовать разработке более эффективных политик и стратегий по борьбе с изменением климата.

Цель исследования

Целью настоящей статьи было исследование влияния природоохранных инвестиций в основной капитал на снижение выбросов СО2 в атмосферу от стационарных источников в странах Евразийского экономического союза после создания названного межгосударственного образования.

Научная новизна

Новизна исследования состоит в применении непараметрических методов оценки влияния «зеленых» инвестиций на объемы выбросов СО2 в странах Евразийского экономического союза, построении соответствующих регрессионных моделей и их проверке на гетероскедастичность с помощью теста Бройша-Пагана.

Авторская гипотеза

Наша гипотеза состоит в том, что между величиной инвестиций в природоохранные мероприятия стран ЕАЭС и объемами выбросов СО2 от стационарных источников в указанных странах отсутствует статистически значимая зависимость, поэтому зафиксированное ранее снижение объемов загрязняющих атмосферу выбросов объясняется не эффективностью мероприятий, направленных на защиту экологии, а иными причинами.

Методология

Статистический анализ и визуализация его результатов выполнены нами с использованием языка R, версия 4.2.2, в операционной системе Windows 10 (64-bit, сборка 18363).

Мы использовали три модели корреляции для исследования взаимосвязи между величиной природоохранных инвестиций и объемами выбросов СО2 в страна Евразийского экономического союза. В параметрическом анализе предполагается, что данные следуют определенному статистическому распределению, обычно нормальному распределению. Один из наиболее часто используемых параметрических методов для оценки корреляции между двумя переменными является коэффициент корреляции Пирсона.

Коэффициент корреляции Пирсона является числовой мерой, которая количественно определяет силу и направление линейной связи между двумя переменными. Он находится в диапазоне от -1 до 1, где значение 1 указывает на положительную линейную корреляцию, значение -1 указывает на отрицательную линейную корреляцию, а значение 0 указывает на отсутствие линейной корреляции между переменными.

Параметрические методы основываются на определенных предположениях о распределении данных. Коэффициент корреляции Пирсона часто используется для количественной оценки линейной связи между двумя непрерывными переменными.

В непараметрическом анализе не делаются предположения о распределении данных. Вместо этого используются статистические тесты, основанные на ранжировании данных. Среди популярных непараметрических коэффициентов корреляции выделяется коэффициент Спирмена.

Коэффициент корреляции Спирмена оценивает монотонную связь между двумя переменными, и его значения находятся в диапазоне от -1 до 1. Он вычисляется на основе относительных ранговых позиций наблюдений.

Непараметрические методы не накладывают жестких предположений относительно распределения данных. Вместо этого они оценивают связь между переменными на основе их порядкового или рангового положения. Примером широко используемой непараметрической меры корреляции является коэффициент корреляции Спирмена.

Методы оценки устойчивой корреляции разработаны для смягчения влияния выбросов и аномальных наблюдений в данных. Эта методология направлена на уменьшение влияния экстремальных значений на оценку корреляций.

Один из заметных коэффициентов устойчивой корреляции – это коэффициент корреляции Мейера, также известный как коэффициент Кендалла. Он разработан для надежной оценки корреляции между переменными путем включения информации о ранжировании.

Осознавая важность учета влияния выбросов и экстремальных значений, методы оценки устойчивой корреляции применяются для получения более надежных оценок корреляций. Среди этих методов широко применяется коэффициент корреляции Кендалла (также называемый коэффициентом корреляции рангов Кендалла).

Мы провели тест Бройша-Пагана, также известный как тест на гетероскедастичность, чтобы проверить гипотезу о гетероскедастичности в наших моделях регрессии.

Гетероскедастичность относится к неравномерному распределению ошибок в модели в зависимости от значений независимых переменных. Это может привести к неправильным выводам и несогласованным оценкам коэффициентов регрессии. Тест Бройша-Пагана позволяет определить гетероскедастичность в остатках модели и принять соответствующие меры.

Статистика теста Бройша-Пагана следует распределению хи-квадрат с числом степеней свободы, равным количеству независимых переменных в исходной модели.

При проведении теста мы сравниваем значение статистики теста Бройша-Пагана с критическим значением распределения хи-квадрат при заданном уровне значимости. Если значение статистики превышает критическое значение, мы приходим к выводу, что в остатках модели есть гетероскедастичность. В противном случае гипотеза о гетероскедастичности отвергается.

Для каждой страны-члена ЕАЭС нами были построены регрессионные модели для изучения влияния инвестиций в природоохранные мероприятия (так называемые «зеленые» инвестиции, инвестиции в основной капитал на охрану атмосферного воздуха, миллионов единиц национальной валюты) на выбросы CO2 (выбросы в атмосферу стационарными источниками, тыс. тонн). Нулевая гипотеза предполагает отсутствие корреляции между величиной «зелены» инвестиций стран-членов ЕАЭС и уровнем выбросов CO2. Для получения стандартизированных параметров модели использовались имеющиеся статистические данные [2; 3]. Доверительные интервалы на уровне 95% и значения p-значений были рассчитаны с использованием аппроксимации Уолда с t-распределением.

На диаграммах и описании регрессионных моделей ниже мы использовали следующие обозначения:

- “emiss_rus”, “emiss_blr”, “emiss_kzh”, “emiss_kyr” – выбросы СО2 от стационарных источников, тыс. тонн, в России, Белоруссия, Казахстане и Киргизии соответственно;

- “inv.env.inv_russ”, “inv.env.inv_blr”, “inv.env.inv_kzh”, “inv.env.inv_kyr” – инвестиции в основной капитал на охрану атмосферного воздуха, миллионов единиц национальной валюты в России, Белоруссии, Казахстане, Киргизии соответственно.

Результаты

Ниже представлены результаты корреляционного и регрессионного анализа влияния природоохранных инвестиций стран Евразийского экономического союза на выбросы СО2 от стационарных источников в названных странах.

1. Модель для России

На рисунке 1 представлены результаты корреляционного анализа с использованием коэффициента Пирсона:

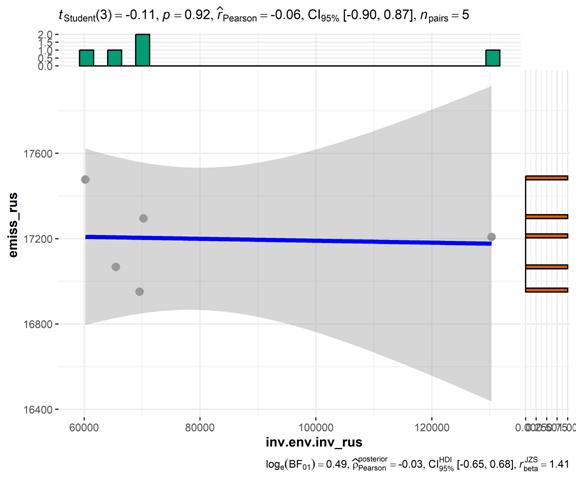
Рисунок 1 – Корреляция (метод Пирсона) между инвестициями в основной капитал на охрану атмосферного воздуха и выбросами СО2 в атмосферу стационарными источниками, Россия. Источник: подготовлено авторами.

Согласно результатам, представленным на рис. 1, значение p-value составляет -0,06. Это значение близко к стандартному значению p-value (0,05), что может свидетельствовать о том, что между наблюдаемыми переменными существует статистически значимая связь, и рост природоохранных инвестиций в России в анализируемый период приводит к снижению выбросов СО2 в атмосферу от стационарных источников.

На рисунке 2 мы представили результаты корреляционного анализа с использованием коэффициента Спирмена:

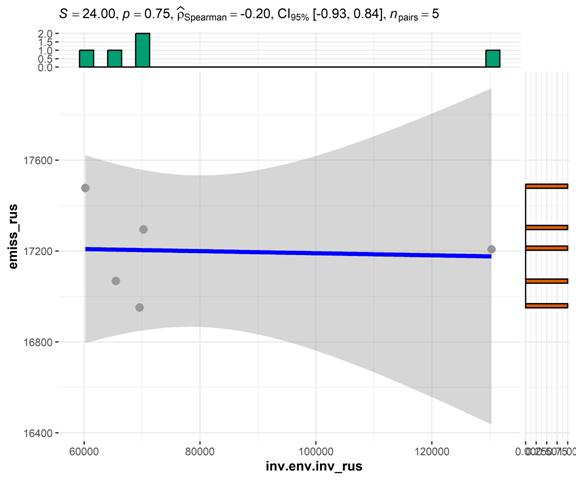
Рисунок 2 – Корреляция (метод Спирмена) между инвестициями в основной капитал на охрану атмосферного воздуха и выбросами СО2 в атмосферу стационарными источниками, Россия. Источник: подготовлено авторами.

Согласно результатам, представленным на рис. 2, значение p-value составляет -0,2. Это значение превышает стандартное значению p-value (0,05), что указывает на недостаточность доказательств для отклонения нулевой гипотезы, т.е. между наблюдаемыми переменными отсутствует статистически значимая связь.

На рисунке 3 представлены результаты корреляционного анализа с использованием коэффициента Кендалла:

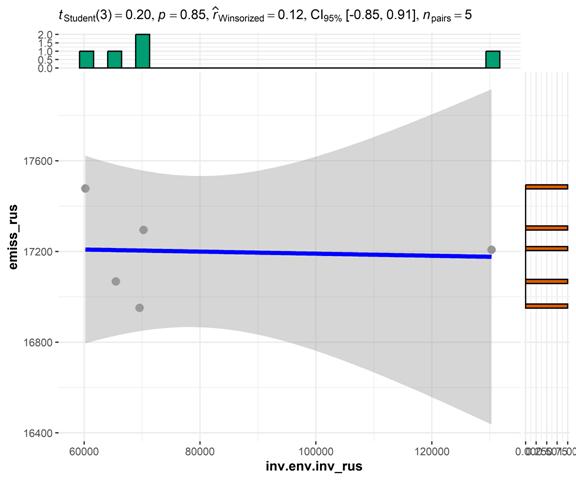
Рисунок 3 – Корреляция (метод Кендалла) между инвестициями в основной капитал на охрану атмосферного воздуха и выбросами СО2 в атмосферу стационарными источниками, Россия. Источник: подготовлено авторами.

Согласно результатам, представленным на рис. 3, значение p-value составляет 0,12. Это значение превышает стандартное значению p-value (0,05), что указывает на недостаточность доказательств для отклонения нулевой гипотезы, т.е. между наблюдаемыми переменными отсутствует статистически значимая связь.

Ниже представлена информация, которая является результатом выполнения регрессионного анализа. Модель (рис. 4), которая была использована, имеет зависимую переменную ‘emiss_rus’ и независимую переменную ‘inv.env.inv_rus’. Результаты анализа включают в себя оценки коэффициентов, их стандартные ошибки, t-значения, p-значения и дополнительные статистические показатели.

Оценки коэффициентов показывают, что константа (Intercept) составляет примерно 1.724e+04, а коэффициент независимой переменной (inv.env.inv_rus) составляет примерно -4.573e-04 (в экспоненциальной записи). Стандартные ошибки коэффициентов отражают их точность оценки.

t-значения используются для проверки значимости коэффициентов. В данном случае, t-значение для константы составляет около 51.033, что указывает на его статистическую значимость. Однако, t-значение для коэффициента независимой переменной составляет около -0.113, что указывает на его незначимость.

p-значения также используются для оценки статистической значимости коэффициентов. В данном случае, p-значение для константы составляет примерно 1.66e-05, что означает, что этот коэффициент статистически значим. Однако, p-значение для коэффициента независимой переменной составляет около 0.917, что означает, что этот коэффициент не является статистически значимым.

Стандартная ошибка остатков модели (Residual standard error) составляет около 234.2.

Множественный коэффициент детерминации и Скорректированный коэффициент детерминации (Multiple R-squared и Adjusted R-squared) показывают, насколько хорошо модель объясняет изменчивость зависимой переменной. В данном случае, Multiple R-squared составляет около 0.004219, что означает, что только около 0,42% изменчивости переменной ‘emiss_rus’ объясняется независимой переменной ‘inv.env.inv_rus’. Adjusted R-squared составляет около -0.3277, что указывает на то, что добавление этой независимой переменной не улучшает предсказательную способность модели.

F-statistic и p-value относятся к статистическому тесту на значимость модели в целом. Здесь F-statistic равен примерно 0.01271 с 1 и 3 степенями свободы, а p-value равно примерно 0.9174. Поскольку p-значение выше обычной уровня значимости 0.05, мы не можем отклонить нулевую гипотезу о том, что модель не имеет статистически значимого эффекта.

Тест Бройша-Пагана используется для проверки гетероскедастичности остатков. Его значение равно примерно 1.7835 с 1 степенью свободы, а p-значение равно примерно 0.1817. Поскольку p-значение выше обычной уровня значимости 0,05, мы не можем отклонить нулевую гипотезу о отсутствии гетероскедастичности в остатках модели.

В целом, результаты регрессионного анализа показывают, что независимая переменная ‘inv.env.inv_rus’ не имеет статистически значимого влияния на зависимую переменную ‘emiss_rus’. Предсказательная способность модели также низкая, объясняя только около 0,42% изменчивости зависимой переменной. Однако, остатки модели не указывают на присутствие гетероскедастичности. Тем не менее, проведенный нами тест Бройша-Пагана дают следующие результаты: BP = 1.7835, df = 1, p-value = 0.1817, свидетельствуя о наличии гетероскедастичности в модели.

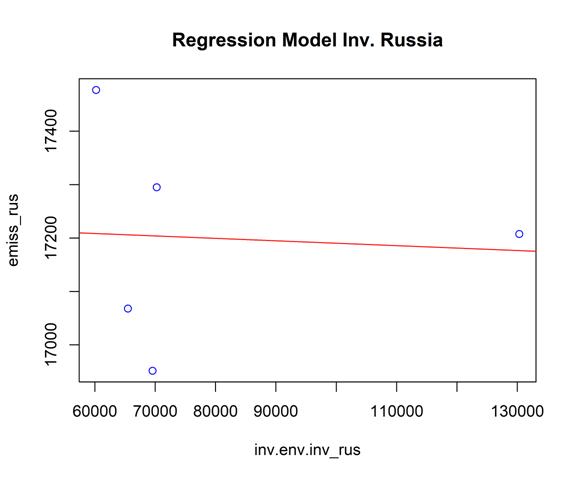
Рисунок 4 – Регрессионная модель зависимости загрязняющих атмосферу выбросов стационарными источниками от инвестиций в природоохранные мероприятия в России. Источник: подготовлено авторами.

Мы построили линейную модель (рис. 4), оцениваемую с помощью метода наименьших квадратов (далее – МНК), для прогнозирования переменной ‘emiss_rus’ с использованием переменной ‘inv.env.inv_rus’ (формула: emiss_rus ~ inv.env.inv_rus). Модель объясняет статистически незначимую и очень слабую долю дисперсии (R2 = 4.22e-03, F(1, 3) = 0.01, p = 0.917, скорр. R2 = -0.33).

Значение константы модели, соответствующее ‘inv.env.inv_rus’ = 0, составляет 17236.18 (95% доверительный интервал (далее – ДИ) [16161.32, 18311.04], t(3) = 51.03, p < 0.001).

В рамках этой модели:

- Влияние переменной ‘inv.env.inv_rus’ является статистически не значимым и отрицательным (бета = -4.57e-04, 95% ДИ [-0.01, 0.01], t(3) = -0.11, p = 0.917; Стандартизованная бета = -0.06, 95% ДИ [-1.90, 1.77]).

2. Модель для Армении

По Армении отсутствуют данные об инвестициях в природоохранные мероприятия в анализируемый период в использованном источнике.

3. Модель для Беларуси

На рисунке 5 представлены результаты корреляционного анализа с использованием коэффициента Пирсона:

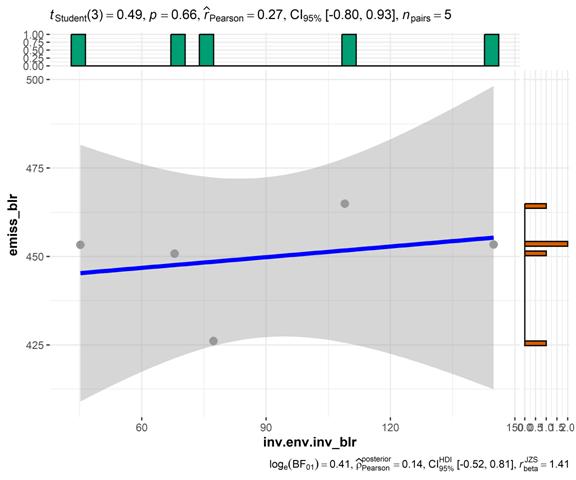
Рисунок 5 – Корреляция (метод Пирсона) между инвестициями в основной капитал на охрану атмосферного воздуха и выбросами СО2 в атмосферу стационарными источниками, Белоруссия. Источник: подготовлено авторами.

На рисунке 6 представлены результаты корреляционного анализа с использованием коэффициента Спирмена:

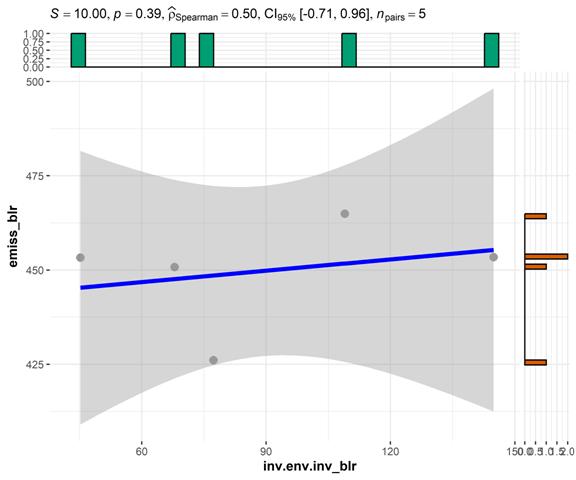
Рисунок 6 – Корреляция (метод Спирмена) между инвестициями в основной капитал на охрану атмосферного воздуха и выбросами СО2 в атмосферу стационарными источниками, Белоруссия. Источник: подготовлено авторами.

На рисунке 7 представлены результаты корреляционного анализа с использованием коэффициента Кендалла:

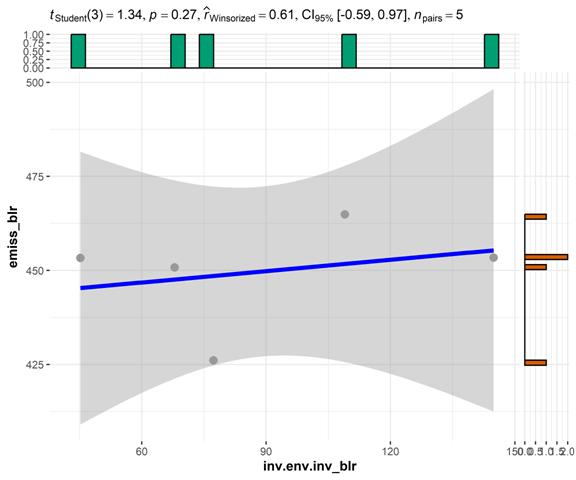
Рисунок 7 – Корреляция (метод Кендалла) между инвестициями в основной капитал на охрану атмосферного воздуха и выбросами СО2 в атмосферу стационарными источниками, Белоруссия. Источник: подготовлено авторами.

Информация ниже является результатом выполнения регрессионного анализа. Модель, которая была использована, имеет зависимую переменную ‘emiss_blr’ и независимую переменную ‘inv.env.inv_blr’. Результаты анализа включают в себя оценки коэффициентов, их стандартные ошибки, t-значения, p-значения и дополнительные статистические показатели.

Оценки коэффициентов показывают, что константа (Intercept) составляет примерно 440.7619, а коэффициент независимой переменной (inv.env.inv_blr) составляет примерно 0.1006. Стандартные ошибки коэффициентов отражают их точность оценки.

t-значения используются для проверки значимости коэффициентов. В данном случае, t-значение для углового коэффициента составляет около 22.608, что указывает на его статистическую значимость. Однако, t-значение для коэффициента независимой переменной составляет около 0.492, что указывает на его незначимость.

p-значения также используются для оценки статистической значимости коэффициентов. В данном случае, p-значение для константы составляет примерно 0.00019, что является статистически значимым на уровне значимости 0.001. Однако, p-значение для коэффициента независимой переменной составляет примерно 0.65634, что указывает на его незначимость на уровне значимости 0.05.

Residual standard error (стандартная ошибка остатков) показывает разброс остатков вокруг регрессионной линии. В данном случае, она составляет примерно 15.86.

Multiple R-squared (коэффициент множественной корреляции) показывает, как хорошо модель объясняет вариацию зависимой переменной. В данном случае, он составляет примерно 0.07472, что означает, что модель объясняет только 7.472% вариации зависимой переменной. Adjusted R-squared (скорректированный коэффициент множественной корреляции) учитывает количество использованных переменных и может быть отрицательным. В данном случае, он составляет около -0.2337.

F-statistic (F-статистика) используется для проверки общей значимости модели. В данном случае, F-статистика составляет примерно 0.2423, а p-значение составляет около 0.6563. Это означает, что модель не является статистически значимой на уровне значимости 0.05.

Тест Бройша-Пагана выполняется для проверки гетероскедастичности остатков. В данном случае, рассчитанное значение статистики BP составляет около 0.12508, а p-значение составляет примерно 0.7236. Это означает, что гетероскедастичность остатков не является статистически значимой на уровне значимости 0.05.

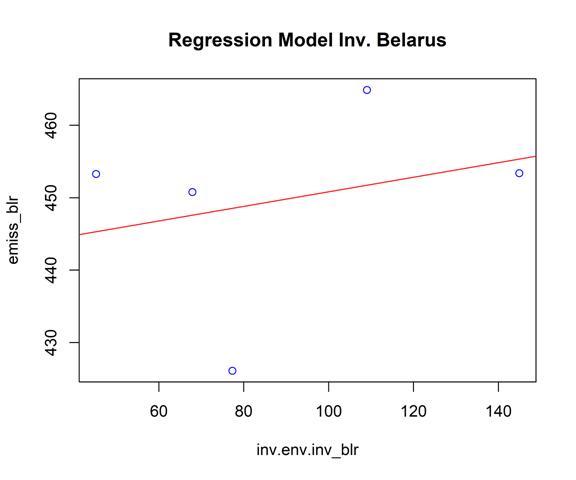
Рисунок 8 – Регрессионная модель зависимости загрязняющих атмосферу выбросов стационарными источниками от инвестиций в природоохранные мероприятия в Белоруссии. Источник: подготовлено авторами.

Мы применили линейную модель (рис. 8) (оцениваемую с помощью МНК) для прогнозирования показателя «emiss_blr» на основе переменной «inv.env.inv_blr» (формула: emiss_blr ~ inv.env.inv_blr). Модель объясняет статистически незначимую и слабую долю вариации (R2 = 0,07, F(1, 3) = 0,24, p = 0,656, скорректированный R2 = -0,23). Значение пересечения модели при inv.env.inv_blr = 0 составляет 440,76 (95% ДИ [378,72, 502,81], t(3) = 22,61, p < 0,001).

В рамках этой модели:

- Влияние переменной inv.env.inv_blr статистически незначимо и положительно (beta = 0,10, 95% ДИ [-0,55, 0,75], t(3) = 0,49, p = 0,656; Std. beta = 0,27, 95% ДИ [-1,49, 2,04]).

4. Модель для Казахстана

На рисунке 9 представлены результаты корреляционного анализа с использованием коэффициента Пирсона:

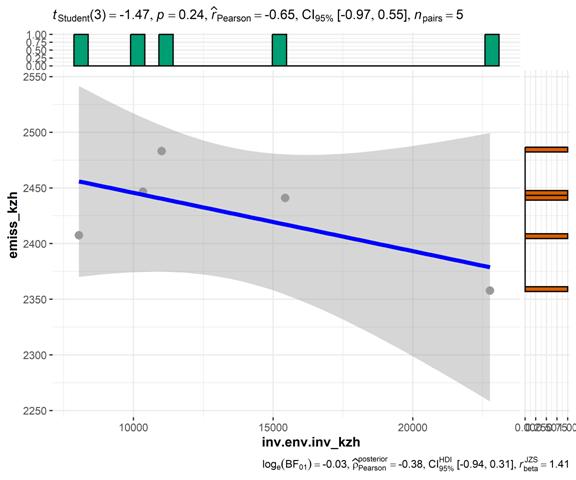
Рисунок 9 – Корреляция (метод Пирсона) между инвестициями в основной капитал на охрану атмосферного воздуха и выбросами СО2 в атмосферу стационарными источниками, Казахстан. Источник: подготовлено авторами.

На рисунке 10 представлены результаты корреляционного анализа с использованием коэффициента Спирмена:

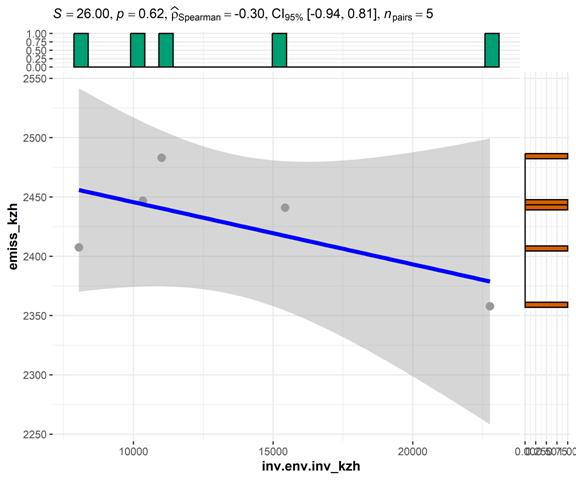
Рисунок 10 – Корреляция (метод Спирмена) между инвестициями в основной капитал на охрану атмосферного воздуха и выбросами СО2 в атмосферу стационарными источниками, Казахстан. Источник: подготовлено авторами.

На рисунке 11 представлены результаты корреляционного анализа с использованием коэффициента Кендалла:

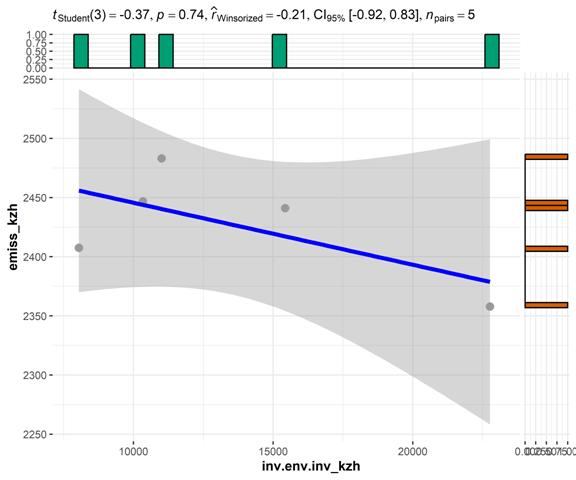
Рисунок 11 – Корреляция (метод Кендалла) между инвестициями в основной капитал на охрану атмосферного воздуха и выбросами СО2 в атмосферу стационарными источниками, Казахстан. Источник: подготовлено авторами.

Ниже приведены результаты применения модели линейной регрессии для предсказания переменной «emiss_kzh» на основе переменной «inv.env.inv_kzh».

Стандартная ошибка остатков модели: 41.56 при использовании 3 степеней свободы.

F-статистика: 2.154 при использовании 1 и 3 степеней свободы, p-значение: 0.2385.

Оценка коэффициента для переменной «inv.env.inv_kzh» составляет -0.005239. Это говорит о том, что при увеличении значения «inv.env.inv_kzh» на единицу, значение «emiss_kzh» уменьшается на 0.005239 единиц с учетом других предикторов модели.

Коэффициент детерминации (R-квадрат) равен 0.4179 (скорректированный R-квадрат: 0.2239), что означает, что 41.79% вариации в переменной «emiss_kzh» объясняется переменной «inv.env.inv_kzh» и другими предикторами модели.

Тест Бройша-Пагана не обнаружил статистически значимой гетероскедастичности в остатках модели, так как p-значение равно 0.2368 (больше 0.05). Это говорит о том, что дисперсия остатков модели является постоянной.

Также стоит отметить, что коэффициент т-статистики для переменной «inv.env.inv_kzh» равен -1.468, и его p-значение равно 0.239. Это означает, что коэффициент не является статистически значимым на уровне значимости 0.05.

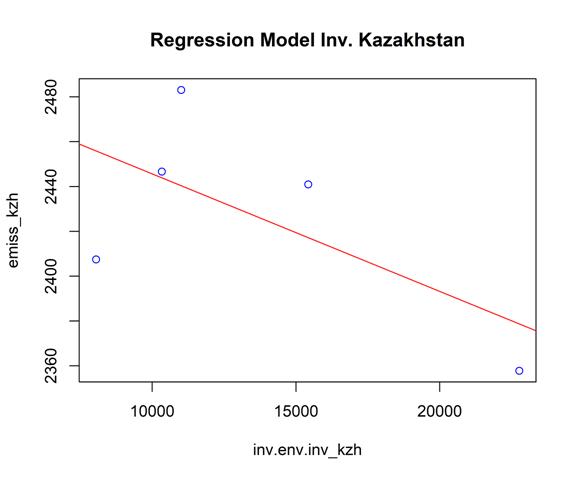
Рисунок 12 – Регрессионная модель зависимости загрязняющих атмосферу выбросов стационарными источниками от инвестиций в природоохранные мероприятия в Казахстане. Источник: подготовлено авторами.

Мы построили линейную модель (рис. 12) (оцениваемую с использованием МНК) для предсказания переменной «emiss_kzh» на основе переменной «inv.env.inv_kzh» (формула: emiss_kzh ~ inv.env.inv_kzh). Модель объясняет статистически незначимую и существенную долю дисперсии (R2 = 0.42, F(1, 3) = 2.15, p = 0.239, скорректированный R2 = 0.22).

Константа модели, соответствующая inv.env.inv_kzh = 0, составляет 2498.03 (95% доверительный интервал [2333.48, 2662.58], t(3) = 48.31, p < .001).

В рамках этой модели:

- Эффект переменной «inv.env.inv_kzh» является статистически незначимым и отрицательным (бета = -5.24e-03, 95% CI [-0.02, 6.12e-03], t(3) = -1.47, p = 0.239; Стандартизированная бета = -0.65, 95% доверительный интервал [-2.05, 0.76]).

Модель, основанная на переменной «inv.env.inv_kzh», не объясняет статистически значимую долю дисперсии переменной «emiss_kzh» (R2 = 0.42). Коэффициент при переменной «inv.env.inv_kzh» оказывается незначимым и отрицательным, что может указывать на отсутствие связи между этими переменными. Доверительные интервалы для коэффициентов позволяют оценить неопределенность оценок.

5. Модель для Киргизии

На рисунке 13 представлены результаты корреляционного анализа с использованием коэффициента Пирсона:

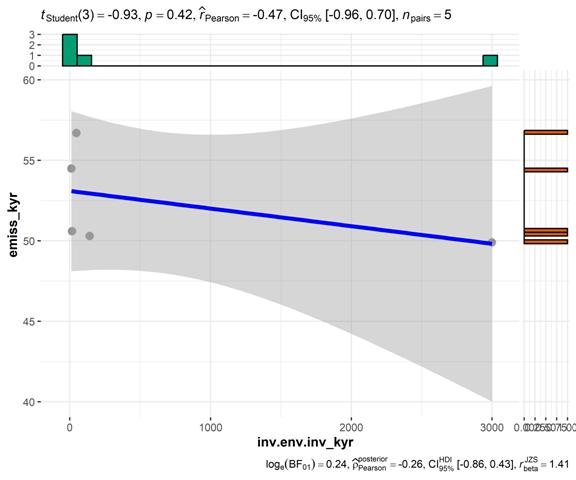
Рисунок 13 – Корреляция (метод Пирсона) между инвестициями в основной капитал на охрану атмосферного воздуха и выбросами СО2 в атмосферу стационарными источниками, Киргизия. Источник: подготовлено авторами.

На рисунке 14 представлены результаты корреляционного анализа с использованием коэффициента Спирмена:

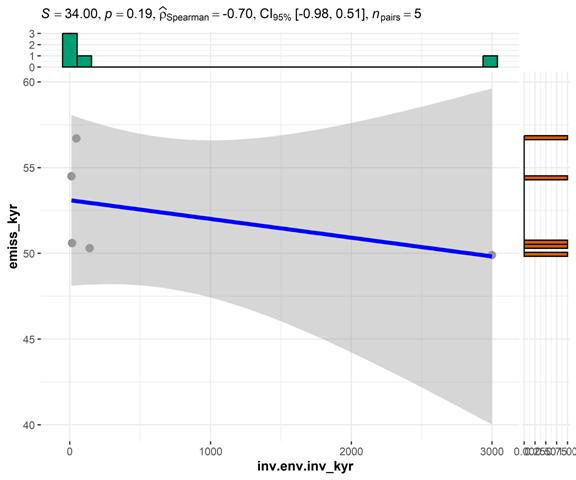
Рисунок 14 – Корреляция (метод Спирмена) между инвестициями в основной капитал на охрану атмосферного воздуха и выбросами СО2 в атмосферу стационарными источниками, Киргизия. Источник: подготовлено авторами.

На рисунке 15 представлены результаты корреляционного анализа с использованием коэффициента Кендалла:

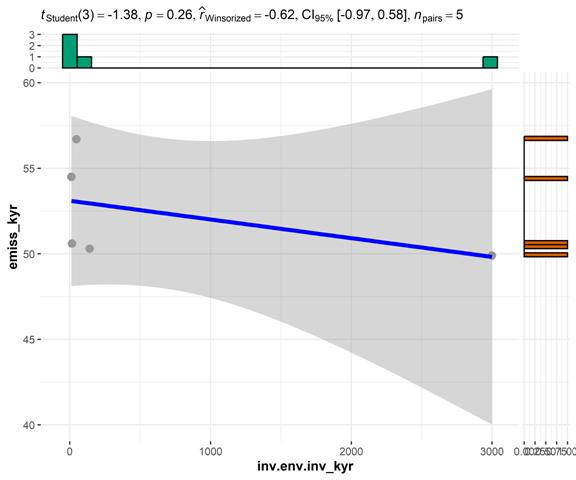
Рисунок 15 – Корреляция (метод Кендалла) между инвестициями в основной капитал на охрану атмосферного воздуха и выбросами СО2 в атмосферу стационарными источниками, Киргизия. Источник: подготовлено авторами.

Ниже представлены результаты применения модели линейной регрессии (рис. 16) для предсказания переменной «emiss_kyr» на основе переменной «inv.env.inv_kyr».

Модель, основанная на переменной «inv.env.inv_kyr», слабо объясняет переменную «emiss_kyr» (R-квадрат = 0.2256). Коэффициент при переменной «inv.env.inv_kyr» оказывается статистически незначимым (p = 0.419), что указывает на отсутствие связи между этими переменными. Остаточная стандартная ошибка: 3.082 при 3 степенях свободы; R-квадрат множественной регрессии: 0.2256, скорректированный R-квадрат: -0.03253. F-статистика F: 0.874 при 1 и 3 степенях свободы, p-значение: 0.4188. Доверительные интервалы для коэффициентов позволяют оценить некоторую неопределенность оценок. Остаточная стандартная ошибка составляет 3.082, что говорит о том, что предсказания модели находятся в среднем в пределах плюс-минус 3.082 от фактического значения.

Тест Бройша-Пагана используется для проверки гомоскедастичности (равномерности дисперсии) остатков модели. В данном случае, результаты теста (BP = 1.8618, p-value = 0.1724) не дают оснований отвергнуть нулевую гипотезу о гомоскедастичности остатков.

Таким образом, модель линейной регрессии не является статистически значимой и не может достаточно хорошо объяснить изменчивость переменной «emiss_kyr» на основе переменной «inv.env.inv_kyr».

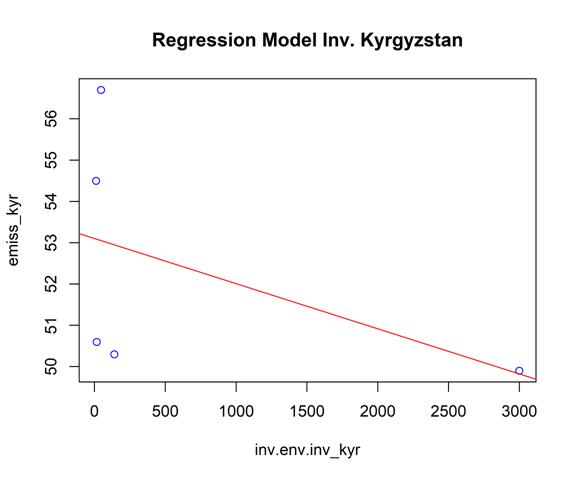
Рисунок 16 – Регрессионная модель зависимости загрязняющих атмосферу выбросов стационарными источниками от инвестиций в природоохранные мероприятия в Киргизии. Источник: подготовлено авторами.

Мы построили линейную модель (рис. 16) (оцениваемую с использованием МНК) для предсказания переменной «emiss_kyr» на основе переменной «inv.env.inv_kyr» (формула: emiss_kyr ~ inv.env.inv_kyr). Модель объясняет статистически незначимую и умеренную долю дисперсии (R2 = 0.23, F(1, 3) = 0.87, p = 0.419, скорректированный R2 = -0.03).

Константа модели, соответствующая inv.env.inv_kyr = 0, составляет 53.10 (95% доверительный интервал [48.11, 58.10], t(3) = 33.83, p < .001).

В рамках этой модели:

- Эффект переменной inv.env.inv_kyr является статистически незначимым и отрицательным (бета = -1.09e-03, 95% доверительный интервал [-4.81e-03, 2.63e-03], t(3) = -0.93, p = 0.419; Стандартизированная бета = -0.47, 95% доверительный интервал [-2.09, 1.14]).

Модель, основанная на переменной «inv.env.inv_kyr», не объясняет статистически значимую долю дисперсии переменной «emiss_kyr» (R2 = 0.23). Коэффициент при переменной «inv.env.inv_kyr» оказывается незначимым и отрицательным, что может указывать на отсутствие связи между этими переменными. Доверительные интервалы для коэффициентов позволяют оценить неопределенность оценок. Однако необходимо отметить, что модель была построена на основе небольшой выборки (N=3), поэтому результаты могут быть менее надежными и не обобщаться на всю генеральную совокупность.

Заключение

Полученные нами результаты достаточно противоречивы. С одной стороны, за исключением Беларуси рост природоохранных инвестиций приводит к снижению выбросов СО2 в атмосферу стран-участниц Евразийского экономического союза. С другой стороны, корреляционный и регрессионный анализ полученных нами моделей не позволил выявить статистически значимого влияния «зеленых» инвестиций на снижение загрязняющих атмосферу выбросов от стационарных источников в названных странах. Мы полагаем, что краткость существования упомянутого международного объединения не позволяют сделать однозначный вывод о взаимосвязи «зеленых» инвестиций и величины выбросов СО2; необходимы дальнейшие исследования. Однако можно утверждать, что переход к более широкому использованию возобновляемых источников энергии потребует роста инвестиций в природоохранные мероприятия, а, значит, появятся новые данные для развития и совершенствования предложенных в настоящей статье моделей.