Системная устойчивость и экономические циклы
Скачать PDF | Загрузок: 27
Статья в журнале
Российское предпринимательство *
№ 7 (55), Июль 2004
* Этот журнал не выпускается в Первом экономическом издательстве
Аннотация:
Окончание. Начало в № 6/2004. Анализ колебательной устойчивости и темпов экономического роста может быть выполнен по спектру собственных значений матрицы G. При этом для количественной оценки уровней демпфирования колебательных составляющих движения будем использовать степень устойчивости системы, которую определим модулем вещественной части самой правой пары сопряженных комплексных корней характеристического уравнения на комплексной плоскости. Аналогично под степенью экономического роста будем понимать значение самого правого вещественного собственного числа.
Ключевые слова: экономический рост, экономические циклы, устойчивость системы, системная устойчивость, цикличность экономики
Окончание. Начало в № 6/2004
Анализ колебательной устойчивости и темпов экономического роста может быть выполнен по спектру собственных значений матрицы G. При этом для количественной оценки уровней демпфирования колебательных составляющих движения будем использовать степень устойчивости системы, которую определим модулем вещественной части самой правой пары сопряженных комплексных корней характеристического уравнения на комплексной плоскости. Аналогично под степенью экономического роста будем понимать значение самого правого вещественного собственного числа.
Для расчетов собственных значений в распоряжении исследователя имеется программная реализация ![]() - алгоритма, реализованная в пакетах прикладных программ и вычислительной среде MATLAB [1].
- алгоритма, реализованная в пакетах прикладных программ и вычислительной среде MATLAB [1].
Обеспечение желаемых или максимально возможных демпферных свойств системы и темпов расширения экономики может быть достигнуто численным поиском элементов вектора конечного спроса или, что то же самое, величин ![]() из формулы (3), то есть нормированием потребления. Разумеется, это не единственно возможный сигнал управления. Так, система таблиц аналитических показателей МОБ, разрабатываемая Госкомстатом России, содержит в матрице коэффициентов прямых затрат А строку и, соответственно, столбец с названием «Услуги финансовых посредников». Их элементы также могут выступать в качестве варьируемых параметров при численной оптимизации динамических свойств экономической системы. Сама оптимизация выполняется в соответствии со схемой алгоритма, представленного на рис. 1.
из формулы (3), то есть нормированием потребления. Разумеется, это не единственно возможный сигнал управления. Так, система таблиц аналитических показателей МОБ, разрабатываемая Госкомстатом России, содержит в матрице коэффициентов прямых затрат А строку и, соответственно, столбец с названием «Услуги финансовых посредников». Их элементы также могут выступать в качестве варьируемых параметров при численной оптимизации динамических свойств экономической системы. Сама оптимизация выполняется в соответствии со схемой алгоритма, представленного на рис. 1.

Рис. 1. Функциональная схема численного поиска
Первоначально на основе статистических данных составляется динамическая модель МОБ. В первом блоке функциональной схемы исходная система приводится к нормальной форме Коши. Далее вычисляются собственные числа матрицы состояния замкнутой модели с помощью QR – алгоритма. По ним формируется вспомогательная функция F, ориентирующаяся на совокупность доминирующих корней, смещение которых на комплексной плоскости в результате введения управления представляется желательным.
На следующем этапе в соответствии с выбранным алгоритмом численного поиска определяется стратегия изменения варьируемых параметров в направлении уменьшения функционала. Для новых значений параметров корректируется матрица системы, вновь вычисляются характеристические корни и т.д.
Для успешной реализации алгоритма численного поиска большое значение имеет минимизируемая вспомогательная функция F, которая должна обладать необходимыми математическими свойствами непрерывности и дифференцируемости и ориентироваться на совокупность корней характеристического уравнения матрицы G модели (6), определяющих динамические свойства системы. Эта функция может быть построена следующим образом:
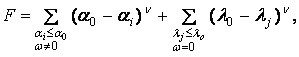 (7)
(7)
где ![]() – собственные числа G;
– собственные числа G; ![]() – параметр, характеризующий желаемое демпфирование колебательных составляющих;
– параметр, характеризующий желаемое демпфирование колебательных составляющих; ![]() – вещественные части комплексных корней, взятые с обратным знаком;
– вещественные части комплексных корней, взятые с обратным знаком; ![]() – требуемая величина степени экономического роста;
– требуемая величина степени экономического роста; ![]() – значения вещественных корней;
– значения вещественных корней; ![]() – параметр (
– параметр (![]() =2,3,4,…).
=2,3,4,…).
Введение управления преследует цель обеспечить смещение на комплексной плоскости комплексных корней до уровня ![]() , вещественных – до
, вещественных – до ![]() , а также обеспечить
, а также обеспечить ![]() . Таким образом, экономическая система должна быть апериодически неустойчивой.
. Таким образом, экономическая система должна быть апериодически неустойчивой.
Весьма актуальным является обеспечение колебательной устойчивости и приемлемой динамики переходных процессов для моделей, учитывающих временные зависимости элементов матриц А и В из (1), т.е. для ![]() , так как, строго говоря, элементы
, так как, строго говоря, элементы ![]() можно только условно считать постоянными. Если определить уравнение (1), записанное для момента времени
можно только условно считать постоянными. Если определить уравнение (1), записанное для момента времени ![]() , как модель k – го "режима" экономической системы и рассмотреть моменты времени
, как модель k – го "режима" экономической системы и рассмотреть моменты времени ![]() , соответствующие изменяющимся технологическим условиям функционирования экономики, то нетрудно сформулировать задачу обеспечения колебательной устойчивости для совокупности "режимов". Это же мероприятие позволяет обеспечить получение так называемых робастных результатов, учитывающих статистическую ошибку в исходных данных. Здесь выбирается единый вектор конечного спроса, а обобщенная функция качества переходных процессов F формируется как сумма критериев вида (7):
, соответствующие изменяющимся технологическим условиям функционирования экономики, то нетрудно сформулировать задачу обеспечения колебательной устойчивости для совокупности "режимов". Это же мероприятие позволяет обеспечить получение так называемых робастных результатов, учитывающих статистическую ошибку в исходных данных. Здесь выбирается единый вектор конечного спроса, а обобщенная функция качества переходных процессов F формируется как сумма критериев вида (7):
 (8)
(8)
где п – число «режимов».
Для функционала (8) возможно, а во многих случаях целесообразно, задавать показатели качества переходных процессов ![]() и
и ![]() различными. Так, для режимов, близких к предельным по устойчивости или нагрузочной способности экономики, они могут выбираться меньшими, чем для «рабочих» режимов.
различными. Так, для режимов, близких к предельным по устойчивости или нагрузочной способности экономики, они могут выбираться меньшими, чем для «рабочих» режимов.
На варьируемые параметры ![]() по инженерно-экономическим и иным соображениям могут быть наложены ограничения. Они учитываются следующей заменой переменных:
по инженерно-экономическим и иным соображениям могут быть наложены ограничения. Они учитываются следующей заменой переменных:
![]() (9)
(9)
с последующей безусловной минимизацией по коэффициентам ![]() .
.
С вычислительной точки зрения с ростом ![]() и
и ![]() вклад слагаемых в сумму (8) возрастает. Таким образом, эти показатели являются своеобразными весовыми коэффициентами функции качества. При этом, как это уже отмечено выше, каждый "режим" характеризуется своей матрицей состояния, по которой вычисляются собственные числа и формируются
вклад слагаемых в сумму (8) возрастает. Таким образом, эти показатели являются своеобразными весовыми коэффициентами функции качества. При этом, как это уже отмечено выше, каждый "режим" характеризуется своей матрицей состояния, по которой вычисляются собственные числа и формируются ![]() . Существенно, что объем вычислений растет лишь линейно с увеличением числа "режимов", что позволяет вести оптимизацию даже при большой размерности задачи.
. Существенно, что объем вычислений растет лишь линейно с увеличением числа "режимов", что позволяет вести оптимизацию даже при большой размерности задачи.
Расчеты по оптимизации спроса с использованием, например, метода покоординатного спуска показали, что это сопряжено с необходимостью вычисления собственных чисел и значений функции ![]() несколько десятков или даже сотен раз. Причем с увеличением числа оптимизируемых параметров
несколько десятков или даже сотен раз. Причем с увеличением числа оптимизируемых параметров ![]() требуемое количество вычислений собственных значений резко возрастает. Известная теоретическая оценка трудоемкости
требуемое количество вычислений собственных значений резко возрастает. Известная теоретическая оценка трудоемкости ![]() - алгоритма для вычисления характеристических корней говорит о том, что она приблизительно пропорциональна кубу размерности вектора переменных состояния. В связи с этим выбор эффективного метода оптимизации является важным условием при работе с высокоразмерными балансовыми моделями. Проанализируем возможные пути снижения объема вычислений.
- алгоритма для вычисления характеристических корней говорит о том, что она приблизительно пропорциональна кубу размерности вектора переменных состояния. В связи с этим выбор эффективного метода оптимизации является важным условием при работе с высокоразмерными балансовыми моделями. Проанализируем возможные пути снижения объема вычислений.
Для минимизации ![]() может быть использован обычный градиентный метод, который с учетом замены переменных (9) принимает вид:
может быть использован обычный градиентный метод, который с учетом замены переменных (9) принимает вид:
![]() (10)
(10)
где ![]() - функция вида (8);
- функция вида (8); ![]() - номер шага;
- номер шага; ![]() - вектор варьируемых параметров;
- вектор варьируемых параметров; ![]() - величина шага вдоль направления вектора градиента.
- величина шага вдоль направления вектора градиента.
Компоненты вектора градиента вычисляются непосредственным дифференцированием (7) и (9):
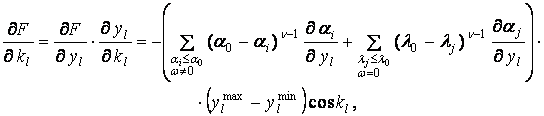 (11)
(11)
где ![]()
![]() ;
; ![]() - элементы матрицы чувствительности, определяемые по известной формуле [2]:
- элементы матрицы чувствительности, определяемые по известной формуле [2]:
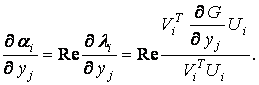 (12)
(12)
Для вещественных корней ![]() во второй сумме выражения (7).
во второй сумме выражения (7).
Здесь ![]() - собственные векторы матриц
- собственные векторы матриц ![]() и
и![]() . При этом
. При этом ![]() представляет собой вещественные части собственных значений в начальной точке, взятые с обратным знаком.
представляет собой вещественные части собственных значений в начальной точке, взятые с обратным знаком.
Стандартная реализация формулы (10) предполагает вычисление всех собственных значений на каждом шаге процесса оптимизации. Число таких шагов при большом числе варьируемых параметров, как уже отмечалось, измеряется десятками и даже сотнями.
Трудоемкость вычислений можно значительно сократить, если использовать в (11) для приближенного вычисления ![]() линейную модель, связывающую изменения значений вектора
линейную модель, связывающую изменения значений вектора ![]() в зависимости от вариации вектора приращения варьируемых параметров
в зависимости от вариации вектора приращения варьируемых параметров ![]() :
:
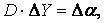 (13)
(13)
где 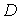 - матрица чувствительностей, элементами которой являются коэффициенты чувствительности
- матрица чувствительностей, элементами которой являются коэффициенты чувствительности ![]() вещественных частей собственных значений к варьируемым параметрам
вещественных частей собственных значений к варьируемым параметрам![]() ;
; ![]()
![]() .
.
Базируясь на линейном прогнозе изменения вещественных частей корней характеристического уравнения (13), можно, как правило, с приемлемой погрешностью выполнить несколько шагов по формуле (10) с заданным шагом ![]() так, чтобы изменение компонент
так, чтобы изменение компонент ![]() и, следовательно,
и, следовательно, ![]() было не слишком велико и оставалось в рамках модели линейного приближения (13).
было не слишком велико и оставалось в рамках модели линейного приближения (13).
Таким образом, значительное число шагов градиентного метода выполняется с вычислением ![]() по формуле (13) без определения всех собственных значений матрицы системы, что значительно сокращает объем вычислений. Когда линейная модель перестает удовлетворять по точности, собственные значения и векторы вычисляются вновь, а затем по ним - матрица чувствительностей
по формуле (13) без определения всех собственных значений матрицы системы, что значительно сокращает объем вычислений. Когда линейная модель перестает удовлетворять по точности, собственные значения и векторы вычисляются вновь, а затем по ним - матрица чувствительностей ![]() для последующего использования системы уравнений (13) на нескольких шагах процесса минимизации.
для последующего использования системы уравнений (13) на нескольких шагах процесса минимизации.
Переход к получению единой настройки для совокупности режимов работы экономической системы не вызывает затруднений, так как компоненты вектора градиента в этом случае легко вычисляются по формуле:
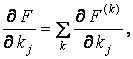
где ![]() - вспомогательная функция для
- вспомогательная функция для ![]() -го режима.
-го режима.
Здесь для каждого режима вычисляется своя матрица чувствительностей ![]() , используемая в (13).
, используемая в (13).
При выборе значения шага ![]() в (10) следует руководствоваться следующими соображениями. Пусть
в (10) следует руководствоваться следующими соображениями. Пусть ![]() ‑ наперед заданное максимально допустимое по условию справедливости линейного прогноза (13) приращение компонент варьируемых параметров
‑ наперед заданное максимально допустимое по условию справедливости линейного прогноза (13) приращение компонент варьируемых параметров ![]() для выполнения нескольких шагов
для выполнения нескольких шагов ![]() по формуле (10) без пересчета матрицы чувствительностей
по формуле (10) без пересчета матрицы чувствительностей ![]() . В соответствии с соотношением (9) ему отвечает некоторое
. В соответствии с соотношением (9) ему отвечает некоторое ![]() . Тогда при известном максимальном значении компонент вектора градиента
. Тогда при известном максимальном значении компонент вектора градиента ![]() значение
значение ![]() , не приводящее к превышению
, не приводящее к превышению ![]() за
за ![]() шагов, определяется выражением
шагов, определяется выражением
![]()
Выводы
1. Показана возможность управления экономической динамикой сложных систем, представленных динамической моделью межотраслевого баланса за счет оптимизации и нормирования конечного потребления и других параметров системы для совокупности режимов их функционирования. Разработан алгоритм оптимизации.
2. Предложен критерий качества переходных процессов для работы в составе алгоритма численного поиска, позволяющий обеспечить заданные или предельно достижимые динамические свойства экономической системы.
3. Высокая вычислительная эффективность оптимизации обеспечивается модификацией градиентного метода, значительно снижающей трудоемкость вычислений по сравнению с традиционными методами (покоординатный спуск, стандартный градиентный метод и др.).
Источники:
2. Уилкинсон Дж. Алгебраическая проблема собственных значений. – М.: Наука, 1970.
Страница обновлена: 22.02.2026 в 02:10:20
Download PDF | Downloads: 27
Sistemnaya ustoychivost i ekonomicheskie tsikly
Toroptsev E.L., Gurnovich T.G.Journal paper
