Разработка модели краткосрочного прогнозирования диапазона изменения цен валютных котировок

Введение

С глобализацией и развитием финансовых отношений, а также совершенствованием информационных технологий, в финансовый рынок вовлекается все большее число участников. Значительная удельная доля участников приходит на рынок с целью получения прибыли от инвестирования и осуществления спекулятивных операций. Рынок ценных бумаг, драгоценных металлов, капитала, товарные и валютные биржи, а также другие финансовые рынки показывают устойчивую тенденцию увеличения денежного оборота. Согласно последним исследованиям Банка международных расчетов, ежедневный денежный оборот валютного рынка Forex в апреле 2016 года составил 5,1 трлн долларов, тогда как в 2000 году он составлял 1,5 трлн долл. [6].

При осуществлении операций на финансовом рынке и принятии решений относительно купли-продажи того или иного финансового актива особое значение имеет прогноз изменения его стоимости. Однако финансовый рынок является сложным для прогнозирования, что обуславливается рядом причин. Если рассматривать валютные курсы, то на их формирование, с одной стороны, влияет состояние экономики страны-эмитента (макроэкономические показатели, торговый баланс и другие). С другой же стороны, сильное воздействие на курсы могут оказывать политические и порой даже психологические факторы. И если курсы, устанавливаемые Центральными банками, более устойчивы, котировки рынка Forex достаточно чувствительны и колеблются практически каждую секунду. Таким образом, механизм формирования цен на валютных и других финансовых рынках чрезвычайно сложен, он включает в себя большое количество факторов, трудных для выявления. Статистические наблюдения, которые имеются в распоряжении исследователей, представляют собой лишь «след» их совместного воздействия, а динамика изменения котировок напоминает хаотические колебания.

В силу описанных выше сложностей сегодня не существует единственного эффективного метода прогнозирования валютных котировок, что делает разработку моделей и методов их прогнозирования актуальной и привлекательной задачей как для практических, так и для научных целей.

Обзор современного состояния изучаемой проблемы

Вопросам прогнозирования динамики изменения цен финансовых активов, в частности валютных курсов, посвящено множество работ. Так, в работах Е.А. Ефремова, П. Панфилова, В.М. Дегтяреева предложены модели прогнозирования валютных курсов с помощью нейронных сетей, которые пользуются все большей популярностью сегодня. Применение различных статистических и эконометрических методов прогнозирования описано в работах Д.В. Колодко, П.А. Иващенко, П.А. Крокова, В.В. Крюковой, В.М. Дегтяреева, В.Д. Летинского. В частности, в работе [3] (Gizatulin, Smirnov, 2003) рассмотрены вопросы применения скользящей средней, адаптивной к типу уравнения тренда при управлении финансовыми активами. Методы теории детерминированного хаоса при анализе обменных курсов применяли А.М. Балонишников, В.А. Балонишникова. Применение методов, связанных с нечеткими временными рядами, рассмотрены в работах К. Дегтярева. Вопросы совершенствования методологии управления динамическим капиталом рассмотрены в работе [4] (Kamnєva, Kholіna, Gіzatulіn, 2012).

Вместе с тем, несмотря на наличие большого количества работ, все еще не существует инструмента, который бы позволил достаточно эффективно прогнозировать цены финансовых инструментов, в частности валютных пар. Также анализ литературы выявил, что большинство работ посвящены повышению точности прогноза их будущей цены. Однако недостаточно проработаны модели и методы, позволяющие прогнозировать наиболее вероятный диапазон изменения валютных котировок.

Описание модели краткосрочного прогнозирования диапазона изменения валютных котировок

В динамике таких показателей, как цены на акции, нефть, золото и курсы валют, крайне сложно выявить устойчивые тенденции, элементы циклического или сезонного поведения. Изменение их стоимости характеризуется хаотичностью и непредсказуемостью, резкими скачками. Этим обуславливается сложность построения точного прогноза, особенно в долгосрочном периоде. Так, авторами работы [2] (Baloshnikov, Baloshnikova, 2010) была выявлена ограниченная предсказуемость курса валют на примере курса доллара к рублю. Ранее, в работе [1] (Baloshnikova, 2009), подобная тенденция была выявлена и по отношению к другим валютам. Тем не менее в работах был сделан вывод о возможности их прогнозирования в краткосрочном периоде.

При прогнозировании динамики финансовых рынков наибольшей популярностью пользуются два основных подхода: фундаментальный и технический анализ. Фундаментальный анализ основывается на том, что при прогнозировании необходимо учитывать влияние макро- и микроэкономических показателей, таких как ВВП, процентные ставки, безработица и другие. В свою очередь, главным постулатом технического анализа является возможность прогнозирования будущей динамики цен с помощью анализа прошлой. Согласно техническому анализу, любое воздействие на цену, будь то экономический или политический фактор, учитывается рынком и находит в ней отражение. Следовательно, чтобы прогнозировать будущее значение цены, необходимо исследование накопленной статистики, которая является «историей» изменения исследуемых величин, представленной в виде временного ряда – множества упорядоченных во времени наблюдений.

В рамках технического анализа можно выделить такую условную группу методов, как канальные индикаторы. Как инструмент анализа рынка, канальные индикаторы получили широкое распространение среди трейдеров. Они позволяют измерять волатильность цены и учитывать ее при осуществлении финансовых операций. Суть использования канальных индикаторов заключается в построении возможных границ колебаний цены. Схожий подход лежит в основе настоящей работы.

Авторами данной работы предлагается осуществить краткосрочный прогноз возможного диапазона колебания будущей цены, то есть определить прогнозный коридор. Фактически он представляет собой интервал, в пределах которого будет находиться наиболее вероятное значение цены.

В основе механизма прогнозирования, предлагаемого авторами данной работы, лежит метод парной регрессии, в то время как большинство канальных индикаторов базируются на скользящей средней. Прогнозирование предлагается осуществлять с использованием уравнения регрессии вида (1).

, (1)

где Y– зависимая, прогнозируемая переменная;

a и b – коэффициенты регрессии;

t – независимая переменная, обозначающая момент времени.

Идентификация параметров а и b осуществляется с помощью метода наименьших квадратов (МНК) на основе статистики баров, содержащих информацию об изменении котировок за определенный период времени.

Постоянно меняющаяся динамика валютных курсов требует разработки гибкого механизма прогнозирования значений временного ряда, т.к. сам временной ряд подвержен значительным колебаниям. При данном подходе в качестве статистики для идентификации параметров предлагается использовать только последние N значений выборки – скользящее окно, а не весь массив статистической информации. Данное предположение основывается на том, что последние значения выборки хранят наиболее актуальную информацию о состоянии на рынке и оказывают наибольшее влияние на ближайшее поведение цены при прогнозировании ее на краткосрочный период. Таким образом, величина N определяет гибкость прогноза.

Границы каналов большинства индикаторов чаще всего строятся исходя из цены закрытия или усредненной цены за период. Например, верхняя и нижняя полосы канала Боллинджера пропорциональны среднеквадратическому отклонению от скользящей средней цены за период. Для построения границ канала Кельтнера необходимо найти скользящие средние от разницы максимальной (High) и минимальной (Low) цены за период.

Подход, предложенный авторами данной работы, заключается в том, что построение верхней и нижней границ прогнозного коридора необходимо основывать на максимальной и минимальной ценах за период. Изменение величины максимума и минимума баров свидетельствует о том, что изменится возможный диапазон вероятных значений будущих цен, а значит, и ширина прогнозного коридора.

Исходя из этого утверждения, для определения верхнего и нижнего значений прогнозного коридора необходимо учитывать разный характер колебания максимальной и минимальной цен. Поэтому в работе предлагается построить два уравнения регрессии вида (1) для верхней и нижней границ коридора соответственно. Идентификация верхней границы осуществляется на основе выборки b_H – максимальных значений баров (High), идентификация нижней, соответственно, b_L – минимальных значений баров (Low). Исходя из этого, границы находятся из выражения 2.

, (2)

где Y (N+1) – фактическое значение курса валют на следующем (прогнозном) шаге;

– прогнозное значение максимальной и минимальной цен бара на следующем шаге;

– величина отклонения верхней и нижней границ коридора.

Для нахождения величин ξ_{H и} ξ_L необходимо для всех значений t(N) выборок b_H и b_L определить абсолютную ошибку ε(N) прогноза как модуль разницы между прогнозным и фактическим значениями. В выражении (3) представлена формула нахождения ошибки в общем виде.

, (3)

где – абсолютная ошибка прогноза;

– фактическое значение курса в момент времени N;

– прогнозное значение валютного курса в момент времени N.

Совокупность этих величин, упорядоченных по возрастанию, составляет множество E (выражение 4).

(4)

Важной величиной при построении прогнозного коридора является процент охвата выборки коридором – величина ν, которая изменяется в пределах от 0 до 1. Согласно МНК, сумма квадратов отклонений прогнозных значений от фактических является минимальной, поэтому получаемая линия регрессии располагается так, что вокруг нее сгруппировано большинство значений выборки. Исходя из этого, можно определить такое граничное значение ξ, в пределах которого будет находится ν процентов прогнозируемой величины. Для упорядоченного множества Е из выражения (4) эту граничную величину можно определить из выражений (5–7):

(5)

, (6)

где Z – множество целых чисел.

Полученное число m является порядковым номером элемента множества Е, которое и является искомой величиной ξ (выражение 7).

(7)

Таким образом, получаем, что, при сохранении предыдущей динамики, значение прогноза с вероятностью ν будет находиться в пределах диапазона, определяемого из выражения (2), что и определяет ширину коридора. Фактически она зависит от того, насколько большими были отклонения прогноза от фактического значения, т.е. от волатильности цены валютной пары. Стоит отметить, что свои особенности на динамику валютных курсов может оказывать и временной интервал баров, т.е. таймфрейм (TF).

Таким образом, полученная модель прогнозирования валютного курса имеет три параметра. В общем виде модель представлена в выражении 8.

, (8)

где P – фактический процент попадания значений курса валют в прогнозный коридор.

Результаты апробации модели

Для апробации представленной модели была использована динамика цены валютной пары EUR/USD за 2015 год, N ϵ [2, 3…30], ν ϵ [60,65…95], таймфреймы – пятиминутный (M5), часовой (H1) и дневной (D1).

Ключевым при использовании изложенного метода прогнозирования является определение оптимальных величин скользящего окна N и вероятности попадания в прогнозный коридор ν для каждого таймфрейма. От этих параметров напрямую зависит ширина прогнозного коридора.

Оценить качество результатов поможет такой показатель, как процент попадания в коридор (Р). При слишком малых значениях N и ν получаем узкий канал, следовательно, маленький процент попадания в коридор (рис. 1а), при больших значениях – слишком широкий коридор, значительно отклоняющийся от реальных значений цены (рис. 1б). В оптимальном случае параметры модели должны быть такими, чтобы прогнозный коридор, с одной стороны, наиболее точно описывал диапазон изменения цены. С другой стороны, его ширина не должна покрывать большие скачки цены, т.к. анализ его прорывов вследствие неожиданных скачков может свидетельствовать об изменении тренда.

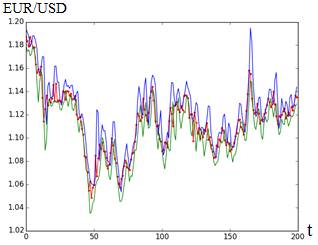
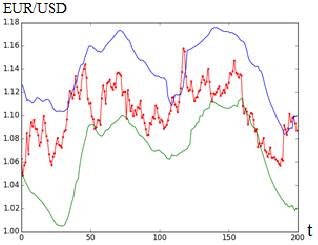
a) б)

Рисунок 1. Графики прогнозного коридора при: а) N=2, ν=0.6, P=45 %; б) N=50, ν=0.95, P=78 %

Источник: составлено автором

При проведении серии экспериментов было выявлено, что с увеличением ν увеличивается и процент попадания в коридор P. Однако при увеличении N процент значимо растет только до определенной границы, которую, при дальнейшем увеличении N, превышает не существенно. Это говорит о том, что эта величина ширины скользящего окна является оптимальной и дальнейшее ее увеличение не имеет смысла, т.к. это приведет только к расширению прогнозного коридора, а значит, к понижению точности прогноза. Оптимальные значения N для разных параметров ν и TF, а также соответствующие им величины Р представлены в таблице. На рисунке 2 представлен график прогнозного коридора при оптимальных параметрах.

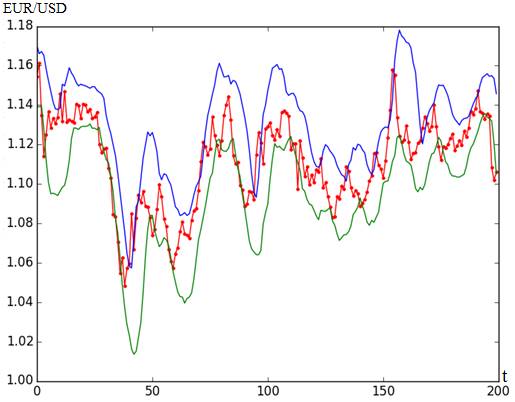
Рисунок 2. График динамики валютной пары EUR/USD и прогнозного коридора при оптимальных значениях параметров: N=13 и ν=0.85, P=80 %

Источник: составлено автором

Таблица

Оптимальные значения N в разрезе величины ν и таймфреймов

Как видно из таблицы, наиболее высокий процент попадания в большинстве случаев был получен при значениях ν от 70–75 %, N от 10 до 13, что говорит о высокой эффективности данных значений параметров при прогнозировании.

Заключение

В данной работе была представлена модель краткосрочного прогнозирования диапазона изменения валютных котировок с тремя параметрами. Апробация модели была осуществлена на примере динамики цен валютных пар EUR/USD за 2015 год. В ходе экспериментов были выявлены оптимальные значения параметров модели (N и ν) для разных таймфреймов. При оптимальных значениях параметров модель показывает высокий процент попадания фактических значений котировок в прогнозный коридор (от 70 % и выше).

Результаты данной работы составляют основу для дальнейших исследований. Разработанная модель обуславливает необходимость изучения характера влияния максимальной и минимальной цен баров динамику цены закрытия. Также в ходе дальнейших исследований предполагается глубже исследовать прикладные аспекты предложенного метода: сформулировать правила купли-продажи, правила входа и выхода с рынка, просчитать прибыльность и другие показатели. Интерес представляет и изучение возможности адаптации параметров модели к различным рыночным ситуациям, в частности эффективность модели в условиях высокой волатильности цены.