Оптимизационная модель сравнительной оценки состояния экономических систем заинтересованными сторонами

Введение. Сравнительная оценка состояния экономических систем и поиск оптимальных решений всегда имели существенное значение для науки и практики [15; 32; 33]. В экономике под системами традиционно понимается обширная совокупность систем (как объектного, так и проектного типов) на различных иерархических уровнях, где верхний эшелон представлен странами и их объединениями, а нижний – бизнес-единицами в составе предприятий и отдельными инвестиционными подпроектами [9–11]. Такого рода анализ востребован многими стейкхолдерами (заинтересованными сторонами): руководителями различных государственных, региональных и муниципальных органов, собственниками, менеджерами, инвесторами, кредиторами и иными участниками экономических процессов [15; 28; 29]. В большинстве ситуаций оценочный процесс индивидуален, но актуален и компромиссный выбор, отвечающий интересам нескольких участников [11; 15]. Комплексность оценки состояния экономических систем, как правило, достигается применением соответствующих групп показателей, то есть проекций [1; 7; 27]. Неоднозначность такого выбора вызвана противоречивостью коэффициентов как внутри групп, так и между ними [8; 12]. Для раскрытия критериальных и стейкхолдерских неопределенностей предложен и апробирован профильный научно-методический аппарат. Принципы, методы и методики многопроекционного и многокритериального выбора, учитывающего интересы сторон, известны [23–25]. В данной статье осуществлена их интеграция в рамках единой оптимизационной стейкхолдерской модели.

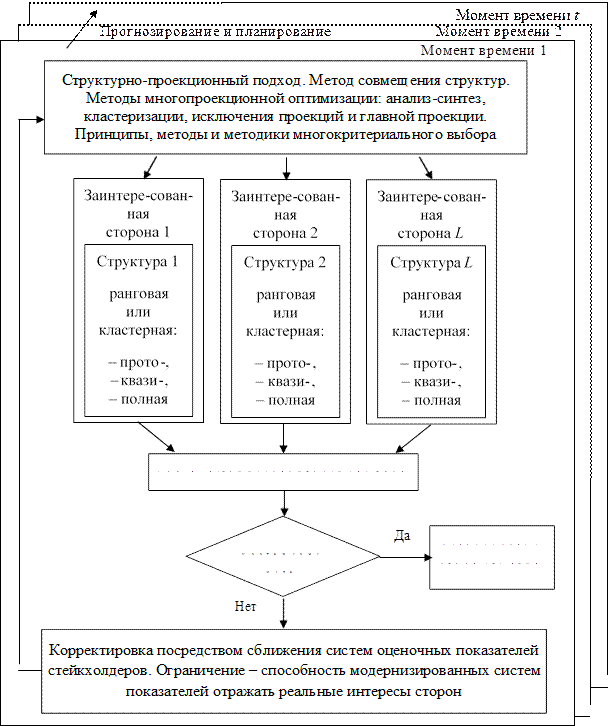
Описание модели. Оптимизационная модель сравнительной оценки состояния экономических систем заинтересованными сторонами приведена на рис. 1. На переднем плане изображен некоторый актуальный момент времени. Базис модели составляют структурно-проекционный подход, метод совмещения структур, методы многопроекционной оптимизации (анализ-синтез, кластеризации, исключения проекций и главной проекции), а также принципы, методы и методики многокритериального выбора. Все они перечислены в головной (верхней) части оптимизационной стейкхолдерской модели [20; 21; 24].

Взаимодействуют несколько заинтересованных сторон (стейкхолдеров) С = {Сl}, , руководствующихся собственными целями Цl = {Цl_i}, , в области обеспечения устойчивости, безопасности, инновационности, эффективности и пр. [6; 26; 30], предусматривающими в том числе потребность достижения согласия при проведении оценки экономического состояния. В детерминированной постановке сравнению подлежат варианты (альтернативы) S = {S_i}, . Интересы стейкхолдеров отражают системы показателей К = {Кlⁱ_j}, , , [24]. Строчный индекс l обозначает принадлежность проекционной системы конкретной заинтересованной стороне, верхний индекс i указывает номер проекции, а нижний j – номер показателя в ней.

Изначально посредством многопроекционной и/или многокритериальной оптимизации формируются индивидуальные решения стейкхолдеров в виде прото-, квази- или полных структур. В многокритериальной постановке выделяют ранговые, а в многопроекционной – кластерные структуры.

Многопроекционное решение синтезируется путем пересечения оптимальных множеств проекций [24; 25], полученных на базе лучших систем (1), эффективных вариантов (2), альтернатив нижестоящих рангов (3):

Рисунок 1. Оптимизационная модель сравнительной оценки состояния

экономических систем заинтересованными сторонами

Источник: составлено автором.

, (1)

, (2)

. (3)

Выражения (1) – (3) описывают симметричный выбор. Кроме того, возможен асимметричный выбор в соответствии с формулой (4), когда задействуемые для синтеза проекционные множества различаются:

. (4)

Затем по формуле (5) синтезируется взаимоприемлемое решение сторон [15]:

. (5)

Компромиссному выбору способствует сближение систем оценочных показателей участников процесса. Ограничением выступает способность модернизированных систем показателей представлять реальные интересы сторон. Излишне компромиссные системы показателей приводят к решениям, которые перестают устраивать стейкхолдеров, поскольку по факту уже не отражают их позицию. Модель позволяет формировать как симметричные, так и асимметричные решения не только в контексте проекций, но и в аспекте учета интересов сторон.

Таким образом, модель обеспечивает получение результата, отвечающего запросам всех взаимодействующих стейкхолдеров. Чтобы перейти к будущему моменту времени, предстоит реализовать надлежащее прогнозирование (планирование) состояния экономических систем.

Моделирование. Поясним специфику оптимизационной стейкхолдерской модели характерными примерами. Полагаем, что осуществляется поиск взаимоприемлемого решения при оценке состояния экономических систем S₁–S₁₀ двумя заинтересованными сторонами. Первая заинтересованная сторона оперирует пятнадцатью показателями в составе пяти проекций К1¹₁–К1¹₃, К1²₁–К1²₃, К1³₁–К1³₃, К1⁴₁–К1⁴₃ и К1⁵₁–К1⁵₃. Как отмечалось ранее, строчный индекс – номер стейкхолдера, верхний индекс – номер проекции, а нижний индекс – номер показателя в ней.

Не производя дополнительных расчетов, воспользуемся сортированными массивами и решениями, изложенными в авторской статье [10], адресуя их первому стейкхолдеру.

Первая проекция.

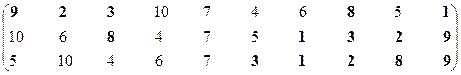
Множество эффективных экономических систем [10] – М1¹_эф = {S₁, S₂, S₃, S₈, S₉}. Здесь и далее в массивах эффективные варианты выделены жирным шрифтом.

Вторая проекция.

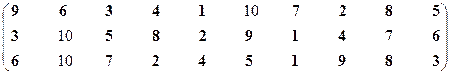
Множество эффективных систем – М1²_эф = {S₁, S₂, S₃, S₄, S₅, S₆, S₇, S₈, S₉}.

Третья проекция.

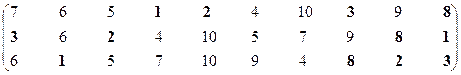
Множество эффективных систем – М1³_эф = {S₁, S₂, S₃, S₈}.

Четвертая проекция.

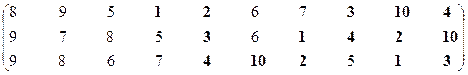
Множество эффективных систем – М1⁴_эф = {S₁, S₂, S₃, S₄, S₁₀}.

Пятая проекция.

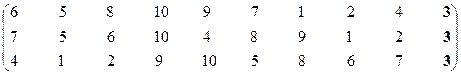
Множество эффективных систем – М1⁵_эф = {S₃}.

Посредством пересечения паретовских множеств проекций определяем первый кластер (протоструктуру) одноименной заинтересованной стороны М1_1КЛ = {S₁, S₂, S₃, S₈, S₉}∩{S₁, S₂, S₃, S₄, S₅, S₆, S₇, S₈, S₉}∩{S₁, S₂, S₃, S₈}∩{S₁, S₂, S₃, S₄, S₁₀}∩{S₃} = {S₃}.

Положим также, что второй стейкхолдер оперирует шестью показателями в составе двух проекций К2¹₁–К2¹₃ и К2²₁–К2²₃ соответственно. Здесь для пояснения сути авторской модели проанализируем восемь возможный ситуаций:

1) все показатели требуется максимизировать;

2) необходимо минимизировать первый и второй показатели и максимизировать третий;

3) требуется минимизировать первый показатель и максимизировать второй и третий;

4) необходимо максимизировать первый и третий показатели и минимизировать второй;

5) требуется максимизировать первый и второй показатели и минимизировать третий;

6) все показатели необходимо минимизировать;

7) требуется минимизировать первый и третий показатели и максимизировать второй;

8) необходимо максимизировать первый показатель и минимизировать второй и третий [11].

Обратимся к сортированным массивам и решениям, представленным в публикации [11]. Только задействуем их не в исходном виде, а преобразуем позиции двух заинтересованных сторон, фигурирующих в [11], в двухпроекционную позицию одного стейкхолдера для целей настоящего исследования. В данной статье это будет сторона 2.

Ситуация 1

Первая проекция.

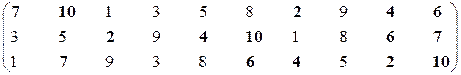
Множество эффективных экономических систем известно [11] – М2¹_эф = {S₂, S₄, S₆, S₇, S₁₀}.

Вторая проекция.

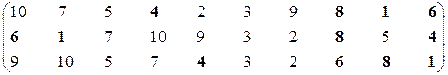
Множество эффективных систем [11] (Lapaev, 2024) – М2²_эф = {S₁, S₄, S₆, S₈}.

Первый кластер (протоструктура) второго стейкхолдера: М2_1КЛ = {S₂, S₄, S₆, S₇, S₁₀}∩{S₁, S₄, S₆, S₈} = {S₄, S₆}.

Ситуация 2

Первая проекция.

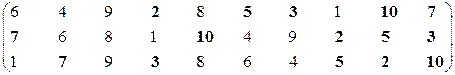
Множество эффективных экономических систем – М2¹_эф = {S₂, S₃, S₅, S₇, S₁₀}.

Вторая проекция.

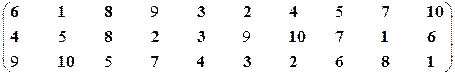
Множество эффективных систем – М2²_эф = {S₁, S₂, S₃, S₄, S₆, S₇, S₈, S₁₀}.

Первый кластер второго стейкхолдера: М2_1КЛ = {S₂, S₃, S₅, S₇, S₁₀}∩{S₁, S₂, S₃, S₄, S₆, S₇, S₈, S₁₀} = {S₂, S₃, S₇, S₁₀}.

Ситуация 3

Первая проекция.

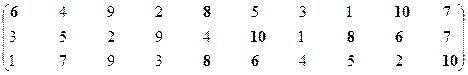
Множество эффективных экономических систем – М2¹_эф = {S₆, S₇, S₈, S₁₀}.

Вторая проекция.

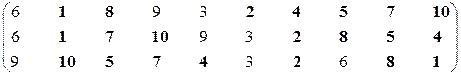
Множество эффективных систем – М2²_эф = {S₁, S₂, S₄, S₅, S₇, S₈, S₁₀}.

Первый кластер второго стейкхолдера: М2_1КЛ = {S₆, S₇, S₈, S₁₀}∩{S₁, S₂, S₄, S₅, S₇, S₈, S₁₀} = {S₇, S₈, S₁₀}.

Ситуация 4

Первая проекция.

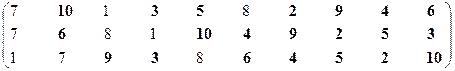
Множество эффективных экономических систем – М2¹_эф = {S₂, S₃, S₄, S₅, S₆, S₉, S₁₀}.

Вторая проекция.

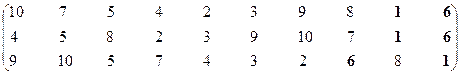
Множество эффективных систем – М2²_эф = {S₁, S₆}.

Первый кластер второго стейкхолдера: М2_1КЛ = {S₂, S₃, S₄, S₅, S₆, S₉, S₁₀}∩{S₁, S₆} = {S₆}.

Ситуация 5

Первая проекция.

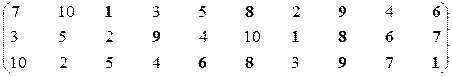
Множество эффективных экономических систем – М2¹_эф = {S₁, S₆, S₇, S₈, S₉}.

Вторая проекция.

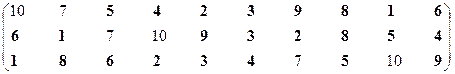
Множество эффективных систем – М2²_эф = {S₁, S₂, S₃, S₄, S₅, S₆, S₈, S₉}.

Первый кластер второго стейкхолдера: М2_1КЛ = {S₁, S₆, S₇, S₈, S₉}∩{S₁, S₂, S₃, S₄, S₅, S₆, S₈, S₉} = {S₁, S₆, S₈, S₉}.

Ситуация 6

Первая проекция.

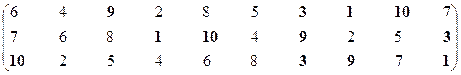
Множество эффективных экономических систем – М2¹_эф = {S₁, S₃, S₇, S₉, S₁₀}.

Вторая проекция.

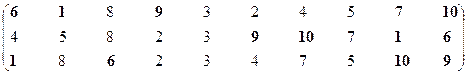
Множество эффективных систем – М2²_эф = {S₁, S₆, S₇, S₉, S₁₀}.

Первый кластер второго стейкхолдера: М2_1КЛ = {S₁, S₃, S₇, S₉, S₁₀}∩{S₁, S₆, S₇, S₉, S₁₀} = {S₁, S₇, S₉, S₁₀}.

Ситуация 7

Первая проекция.

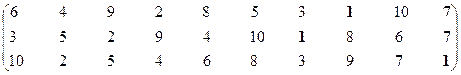
Множество эффективных экономических систем – М2¹_эф = {S₁, S₇}.

Вторая проекция.

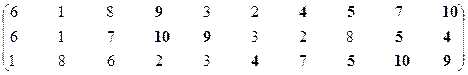
Множество эффективных систем – М2²_эф = {S₄, S₅, S₉, S₁₀}.

Первый кластер второго стейкхолдера отсутствует, поскольку {S₁, S₇}∩{S₄, S₅, S₉, S₁₀} = Ø. Здесь требуется квазиэффективный выбор.

Ситуация 8

Первая проекция.

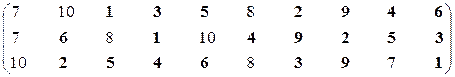
Множество эффективных экономических систем – М2¹_эф = {S₁, S₂, S₃, S₄, S₅, S₆, S₉}.

Вторая проекция.

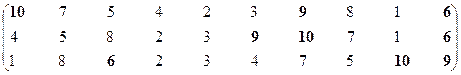
Множество эффективных систем – М2²_эф = {S₆, S₇, S₉, S₁₀}.

Первый кластер второго стейкхолдера: М2_1КЛ = {S₁, S₂, S₃, S₄, S₅, S₆, S₉}∩{S₆, S₇, S₉, S₁₀} = {S₆, S₉}.

Перейдем к синтезу взаимоприемлемых решений двумя заинтересованными сторонами на уровне протоструктур согласно оптимизационной модели. Получаем, что из восьми ситуаций компромисс возможен лишь во второй ситуации, где Мвп_эф = М1_1КЛ∩М2_1КЛ = {S₃}∩{S₂, S₃, S₇, S₁₀} = {S₃}.

Противоречия имеют место и при анализе нижестоящих кластеров, образующих усеченную структуру. Так, с позиции первого стейкхолдера [10] второй кластер имеет вид – М1_2КЛ = {S₂}, а третий – М1_3КЛ = {S₁}. Однако у второй заинтересованной стороны в ситуациях 5 и 6 система S₁ входит в старший первый кластер, а не в третий.

Вариантов коррекции систем оценочных показателей много. Не претендуя в данной статье на их исчерпывающий охват, рассмотрим два характерных случая. Достигая индивидуальной цели при осуществлении сравнительной оценки состояния экономических систем, первый стейкхолдер исключает из рассмотрения заключительную пятую проекцию. Тогда состав первого кластера М1_1КЛ = {S₁, S₂, S₃, S₈, S₉}∩{S₁, S₂, S₃, S₄, S₅, S₆, S₇, S₈, S₉}∩{S₁, S₂, S₃, S₈}∩{S₁, S₂, S₃, S₄, S₁₀} = {S₁, S₂, S₃} расширяется, и наряду со второй ситуацией компромисс станет возможен в ситуациях 5 и 6.

Далее будем полагать, что в ситуации 8 второй стейкхолдер, руководствуясь собственными целевыми установками, заменяет последний показатель на заключительный показатель первой заинтересованной стороны, что отразится на сортированном массиве следующим образом.

Ситуация 8, вторая проекция, модифицированная.

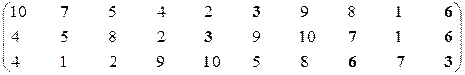
Нетрудно показать, что М2²_эф = {S₃, S₆, S₇}. Учитывая М2¹_эф = {S₁, S₂, S₃, S₄, S₅, S₆, S₉}, находим М2_1КЛ = {S₃, S₆}. В итоге получим точечный ответ Мвп_эф = М1_1КЛ∩М2_1КЛ = {S₃}∩{S₃, S₆} = {S₃}. То есть в данном случае при наличии у сторон общего показателя компромисс достигнут. Суть модели ясна.

Заключение

Разработанная стейкхолдерская модель займет важное место в теории и методологии многокритериальной и многопроекционной оптимизации и будет востребована при формировании профильных подходов, моделей, классификаций, методик и алгоритмов для исследования широкого круга экономических систем на различных иерархических уровнях при решении насущных задач оценки устойчивости [18; 19; 31], безопасности [3; 5; 13], инновационности [14; 16; 17] и эффективности [2; 4; 22] основными заинтересованными сторонами: руководителями министерств, ведомств и департаментов, собственниками, менеджерами, инвесторами, кредиторами и пр.