Метод совмещения структур для исследования экономических систем заинтересованными сторонами
Лапаев Д.Н.1
1 Нижегородский государственный технический университет им. Р.Е. Алексеева
Скачать PDF | Загрузок: 2
Статья в журнале
Креативная экономика (РИНЦ, ВАК)
опубликовать статью | оформить подписку
Том 18, Номер 9 (Сентябрь 2024)
Цитировать:
Лапаев Д.Н. Метод совмещения структур для исследования экономических систем заинтересованными сторонами // Креативная экономика. – 2024. – Том 18. – № 9. – С. 2153-2174. – doi: 10.18334/ce.18.9.121595.
Эта статья проиндексирована РИНЦ, см. https://elibrary.ru/item.asp?id=71960652
Аннотация:
В современных условиях оценка состояния экономических систем различных иерархических уровней преимущественно реализуется в многокритериальной либо в многопроекционной постановках. За проведением такой оценки всегда стоит одна или несколько заинтересованных сторон (стейкхолдеров) в лице: государств, собственников, менеджеров, инвесторов, кредиторов и пр. Предлагаемый в статье метод совмещения структур обеспечивает поиск компромисса заинтересованными сторонами посредством пересечения предварительно выделенных стейкхолдерами индивидуальных ранговых или кластерных прото-, квази- или полных структур. Очевидно, что чем ближе системы показателей заинтересованных сторон друг к другу, тем реальнее компромисс. Однако на пути к согласию следует исключить манипуляции показателями (проекциями) и недоучет интересов стейкхолдеров. Метод совмещения структур станет базовым (в том числе связующим) элементом единой теории и методологии многокритериального и многопроекционного стейкхолдерского выбора и будет востребован при разработке профильных моделей, классификаций, методик и алгоритмов для исследования широкого спектра экономических систем на разных уровнях управления при решении актуальных задач анализа устойчивости, безопасности, инновационности и эффективности различными заинтересованными сторонами
Ключевые слова: экономическая система, заинтересованная сторона, взаимоприемлемое решение, оптимизация, структура, кластер, ранг, устойчивость, безопасность, эффективность
JEL-классификация: С61
Введение
В современных условиях оценка состояния широкого спектра экономических систем различных иерархических уровней в основном осуществляется в многокритериальной либо в многопроекционной постановках [1, 7, 8, 11–14, 16, 17, 19–25, 29] (Alenkova, Lapaeva, 2023; Lapaev, Lapaeva, Potashnik, 2023; Lapaev, 2023; Lapaev, Lapaeva, 2014; Lapaev, 2016; Lapaev, 2024; Lapaev, Lapaeva, Potashnik, 2024; Lapaev, Lapaeva, 2015; Lapaev, Lapaeva, 2014; Lapaeva, 2015; Lapaeva, 2018; Lapaeva, 2017; Lapaeva, 2015; Lapaeva, 2017; Lapaeva, 2017; Lapaeva, 2017; Mityakov [et al.], 2019). Сказанное справедливо для оптимизационных научно-практических задач исследования устойчивости [14, 15, 27] (Lapaev, Lapaeva, Potashnik, 2024; Lapaev, Mityakov, Mokretsova, 2013; Mityakov, Lapaev, Kataeva, Ramazanov, 2019), безопасности [3–6, 9, 10] (Bank, Lapaev, Khusainov, 2024; Bukhvald, Lapaev, 2022; Vakulenko, Lapaev, Vynogradova, Sokolov, 2022; Kuznetsova, Lapaev, 2024; Lapaev, Mityakov, 2013; Lapaev, 2016) и инновационности [2, 11, 17, 18, 26, 28] (Artemyev, Lapaev, Kornilov, Mityakova, 2023; Lapaev, Lapaeva, 2014; Lapaev, Lapaeva, 2014; Lapaeva, Mityakova, 2022; Mityakov, Lapaev, Mityakov, Ladynin, 2022; Morozova, Maltsev, Maltsev, Lapaev, 2010).
За проведением оценки состояния экономических систем всегда стоит некая заинтересованная сторона (стейкхолдер; лицо, принимающее решение). Характерными стейкхолдерами являются: государства, собственники, менеджеры, инвесторы, кредиторы и пр. В большинстве случаев оценочный процесс индивидуален, но востребован и компромиссный выбор, отвечающий интересам нескольких сторон [12, 24, 25] (Lapaev, 2016; Lapaeva, 2017; Lapaeva, 2017), который предстоит конкретизировать.
Предлагаемый в статье метод совмещения структур обеспечивает поиск компромисса заинтересованными сторонами при осуществлении сравнительной оценки состояния экономических систем путем пересечения (наложения) предварительно выделенных стейкхолдерами ранговых или кластерных структур.
Формализованная постановка имеет следующий
вид. Взаимодействуют несколько заинтересованных сторон (стейкхолдеров) С = {Сl},
,
руководствующихся собственными целями Цl = {Цli}, , 
,
предусматривающими в том числе потребность достижения компромисса при
проведении оценки состояния. Исследование может выполняться на конкретную дату
(настоящую, прошедшую, будущую) либо в динамике. В детерминированной постановке
сравнению подлежат варианты (альтернативы) S = {Si}, . Интересы
стейкхолдера отражает иерархическая К = {Кij}, , 
или
планарная система показателей К = {Кj}, . В многосторонней
проекционной постановке задействуют тройную нумерацию коэффициентов: К =
{Кlij}, , , .
Строчный индекс l обозначает
принадлежность проекционной системы конкретной заинтересованной стороне, верхний
индекс i указывает номер проекции, а нижний j
– номер показателя в ней. Стейкхолдеры руководствуются максимально полным набором
показателей (проекций), обеспечивая надлежащий учет всех аспектов оптимизационной
задачи.
Руководствуясь системой принципов сравнительной оценки состояния экономических систем, предложим логическую схему метода совмещения структур, приведенную на рис. 1.
Рисунок 1. Логическая схема метода совмещения структур
в стейкхолдерском выборе
Источник: составлено автором
Суть метода заключается в следующем. Изначально в каждой проекции находятся индивидуальные решения стейкхолдеров Мlопт. Затем синтезируется взаимоприемлемое решение сторон [12] (Lapaev, 2016):
.
В многокритериальной постановке оперируют ранговыми, а в многопроекционной – кластерными структурами. В качестве индивидуальных решений Мlопт могут выступать прото-, квази- или полные структуры. Отметим, что метод допускает корректировку параметров в виде пересмотра состава сравниваемых альтернатив, стейкхолдеров, проекций и показателей, набора принципов и методов оптимизации, инструментария прогнозирования, планирования и импутации данных, даты проведения исследования, исходной цели.
Вполне очевидно, что чем ближе системы оценочных показателей заинтересованных сторон друг к другу, тем реальнее компромисс в виде Мвп. Вместе с тем необходимо исключить манипуляции показателями (проекциями) и недоучет интересов стейкхолдеров.
Для иллюстрации метода изначально обратимся к однопроекционному выбору, полагая что эффективные множества и нижестоящие ранги известны. Осуществляется поиск взаимоприемлемого решения при оценке состояния экономических систем S1–S10 двумя заинтересованными сторонами, каждая из которых оперирует тремя показателями К11–К13 и К21–К23 соответственно. Проанализируем восемь ситуаций:
1) все показатели требуется максимизировать;
2) необходимо минимизировать первый и второй показатели и максимизировать третий;
3) требуется минимизировать первый показатель и максимизировать второй и третий;
4) необходимо максимизировать первый и третий показатели и минимизировать второй;
5) требуется максимизировать первый и второй показатели и минимизировать третий;
6) все показатели необходимо минимизировать;
7) требуется минимизировать первый и третий показатели и максимизировать второй;
8) необходимо максимизировать первый показатель и минимизировать второй и третий.
Многокритериальные позиции стейкхолдеров представлены сортированными массивами, где экономические системы построчно упорядочены по мере возрастания эффективности.
Ситуация 1
Позиция первого стейкхолдера.
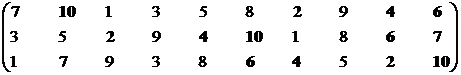
Множество эффективных экономических систем (протоструктура) – М1эф = {S2, S4, S6, S7, S10}.
Позиция второго стейкхолдера.
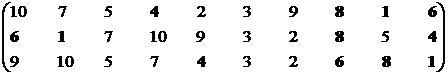
Множество эффективных систем – М2эф = {S1, S4, S6, S8}.
Синтезируем взаимоприемлемое решение на базе протоструктур: Мвпэф = {S2, S4, S6, S7, S10}∩{S1, S4, S6, S8} = {S4, S6}.
Ситуация 2
Позиция первого стейкхолдера.
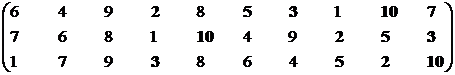
Множество эффективных экономических систем – М1эф = {S2, S3, S5, S7, S10}.
Позиция второго стейкхолдера.
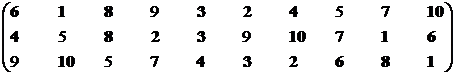
Множество эффективных систем – М2эф = {S1, S2, S3, S4, S6, S7, S8, S10}.
Синтезируем взаимоприемлемое решение: Мвпэф = {S2, S3, S5, S7, S10}∩{S1, S2, S3, S4, S6, S7, S8, S10} = {S2, S3, S7, S10}.
Ситуация 3
Позиция первого стейкхолдера.
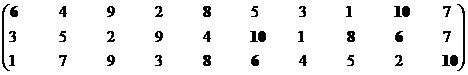
Множество эффективных экономических систем – М1эф = {S6, S7, S8, S10}.
Позиция второго стейкхолдера.
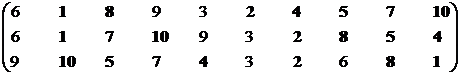
Множество эффективных систем – М2эф = {S1, S2, S4, S5, S7, S8, S10}.
Синтезируем взаимоприемлемое решение: Мвпэф = {S6, S7, S8, S10}∩{S1, S2, S4, S5, S7, S8, S10} = {S7, S8, S10}.
Ситуация 4
Позиция первого стейкхолдера.
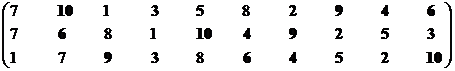
Множество эффективных экономических систем – М1эф = {S2, S3, S4, S5, S6, S9, S10}.
Позиция второго стейкхолдера.
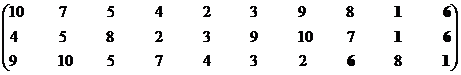
Множество эффективных систем – М2эф = {S1, S6}.
Синтезируем взаимоприемлемое решение: Мвпэф = {S2, S3, S4, S5, S6, S9, S10}∩{S1, S6} = {S6}.
Ситуация 5
Позиция первого стейкхолдера.
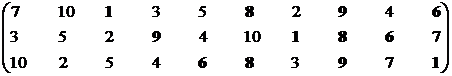
Множество эффективных экономических систем – М1эф = {S1, S6, S7, S8, S9}.
Позиция второго стейкхолдера.
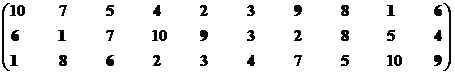
Множество эффективных систем – М2эф = {S1, S2, S3, S4, S5, S6, S8, S9}.
Синтезируем взаимоприемлемое решение: Мвпэф = {S1, S6, S7, S8, S9}∩{S1, S2, S3, S4, S5, S6, S8, S9} = {S1, S6, S8, S9}.
Ситуация 6
Позиция первого стейкхолдера.
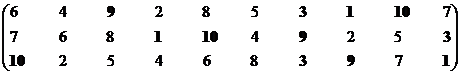
Множество эффективных экономических систем – М1эф = {S1, S3, S7, S9, S10}.
Позиция второго стейкхолдера.
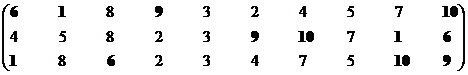
Множество эффективных систем – М2эф = {S1, S6, S7, S9, S10}.
Синтезируем взаимоприемлемое решение: Мвпэф = {S1, S3, S7, S9, S10}∩{S1, S6, S7, S9, S10} = {S1, S7, S9, S10}.
Ситуация 7
Позиция первого стейкхолдера.
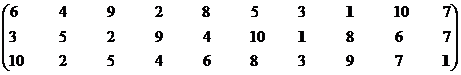
Множество эффективных экономических систем – М1эф = {S1, S7}.
Позиция второго стейкхолдера.
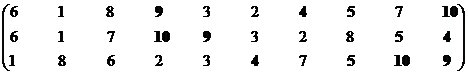
Множество эффективных систем – М2эф = {S4, S5, S9, S10}.
Синтезируем взаимоприемлемое решение: Мвпэф = {S1, S7}∩{S4, S5, S9, S10} = Ø. Здесь стейкхолдеры могут обратиться к квазиэффективному выбору.
Ситуация 8
Позиция первого стейкхолдера.
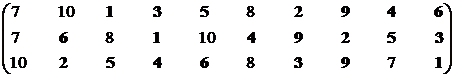
Множество эффективных экономических систем – М1эф = {S1, S2, S3, S4, S5, S6, S9}.
Позиция второго стейкхолдера.
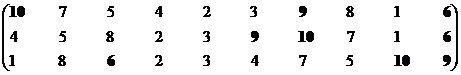
Множество эффективных систем – М2эф = {S6, S7, S9, S10}.
Синтезируем взаимоприемлемое решение: Мвпэф = {S1, S2, S3, S4, S5, S6, S9}∩{S6, S7, S9, S10} = {S6, S9}.
Далее перейдем к рассмотрению вторых рангов.
Ситуация 1
Позиция первого стейкхолдера.
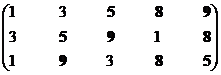
Множество экономических систем второго ранга – М12р = {S5, S8, S9}.
Позиция второго стейкхолдера.
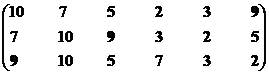
Множество второго ранга – М22р = {S2, S3, S5, S9}.
Синтезируем взаимоприемлемое решение на базе вторых рангов: Мвп2р = {S5, S8, S9}∩{S2, S3, S5, S9} = {S5, S9}.
Ситуация 2
Позиция первого стейкхолдера.
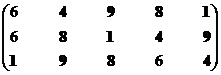
Множество экономических систем второго ранга – М12р = {S1, S4, S8, S9}.
Позиция второго стейкхолдера.
Здесь оставшиеся системы несравнимы и множество второго ранга имеет вид М22р = {S5, S9}.
Синтезируем взаимоприемлемое решение: Мвп2р = {S1, S4, S8, S9}∩{S5, S9} = {S9}. В данном случае ранговые структуры обоих стейкхолдеров проанализированы полностью.
Ситуация 3
Позиция первого стейкхолдера.
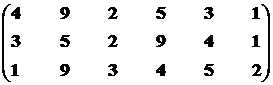
Множество экономических систем второго ранга – М12р = {S1, S2, S3, S4, S5, S9}.
Позиция второго стейкхолдера.
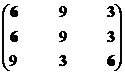
Множество второго ранга – М22р = {S3, S6}.
Синтезируем взаимоприемлемое решение: Мвп2р = {S1, S2, S3, S4, S5, S9}∩{S3, S6} = {S3}.
Ситуация 4
Позиция первого стейкхолдера.
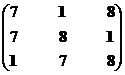
Множество экономических систем второго ранга – М12р = {S1, S8}.
Позиция второго стейкхолдера.
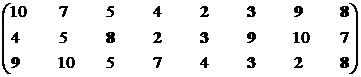
Множество второго ранга – М22р = {S2, S3, S7, S8, S9}.
Синтезируем взаимоприемлемое решение: Мвп2р = {S1, S8}∩{S2, S3, S7, S8, S9} = {S8}.
Ситуация 5
Позиция первого стейкхолдера.
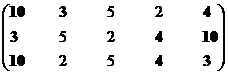
Множество экономических систем второго ранга – М12р = {S3, S4, S10}.
Позиция второго стейкхолдера.
Здесь оставшиеся системы несравнимы и множество второго ранга имеет вид М22р = {S7, S10}.
Синтезируем взаимоприемлемое решение: Мвп2р = {S3, S4, S10}∩{S7, S10} = {S10}.
Ситуация 6
Позиция первого стейкхолдера.
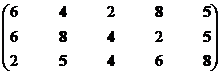
Множество экономических систем второго ранга – М12р = {S4, S5, S8}.
Позиция второго стейкхолдера.
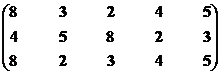
Множество второго ранга – М22р = {S2, S3, S5}.
Синтезируем взаимоприемлемое решение: Мвп2р = {S4, S5, S8}∩{S2, S3, S5} = {S5}.
Ситуация 7
Позиция первого стейкхолдера.
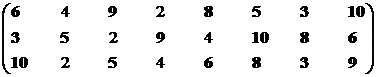
Множество экономических систем второго ранга – М12р = {S3, S5, S6, S8, S9, S10}.
Позиция второго стейкхолдера.
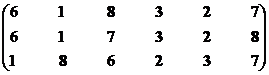
Множество второго ранга – М22р = {S2, S3, S7, S8}.
Синтезируем взаимоприемлемое решение: Мвп2р = {S3, S5, S6, S8, S9, S10}∩{S2, S3, S7, S8} = {S3, S8}.
Ситуация 8
Позиция первого стейкхолдера.
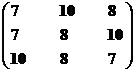
Множество экономических систем второго ранга – М12р = {S7, S8, S10}.
Позиция второго стейкхолдера.
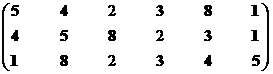
Множество второго ранга – М22р = {S1, S3, S4, S5, S8}.
Синтезируем взаимоприемлемое решение: Мвп2р = {S7, S8, S10}∩{S1, S3, S4, S5, S8} = {S8}.
Далее перейдем к анализу кластерных структур. Осуществляется формирование общего решения при оценке состояния экономических систем S1–S10 двумя заинтересованными сторонами. Первый стейкхолдер оперирует пятью трехкритериальными проекциями (К111–К113, К121–К123, К131–К133, К141–К143 и К151–К153), а второй – двумя (К211–К213 и К221–К223). Необходимо определить взаимоприемлемое решение.
Позиция первого стейкхолдера представлена пятью сортированными массивами, где экономические системы построчно упорядочены по мере роста эффективности. Считаем паретовские множества проекций известными.
Рассмотрим первую проекцию.
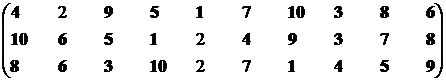
Множество эффективных экономических систем – М11эф = {S1, S3, S5, S6, S7, S8, S9, S10}.
Обратимся ко второй проекции.
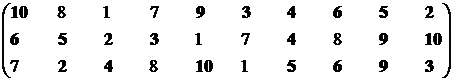
Множество эффективных систем – М12эф = {S2, S3, S4, S5, S6, S9, S10}.
Перейдем к третьей проекции.
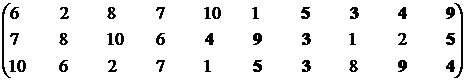
Множество эффективных систем – М13эф = {S3, S4, S5, S9}.
Рассмотрим четвертую проекцию.
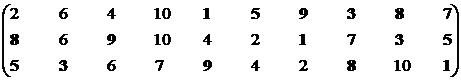
Множество эффективных систем – М14эф = {S1, S3, S5, S7, S8, S9}.
Обратимся к пятой проекции.
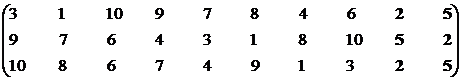
Множество эффективных систем – М15эф = {S2, S5}.
Формируем пятипроекционное эффективное решение (протоструктуру) первой стороны: М1эф = {S1, S3, S5, S6, S7, S8, S9, S10}∩{S2, S3, S4, S5, S6, S9, S10}∩{S3, S4, S5, S9}∩{S1, S3, S5, S7, S8, S9}∩{S2, S5} = {S5}.
Позиция второго стейкхолдера выражена двумя массивами.
Рассмотрим первую проекцию.
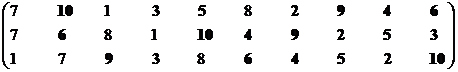
Множество эффективных экономических систем – М21эф = {S2, S3, S4, S5, S6, S9, S10}.
Обратимся ко второй проекции.
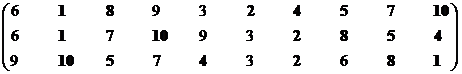
Множество эффективных систем – М22эф = {S1, S2, S4, S5, S7, S8, S10}.
Синтезируем двухпроекционное решение второй стороны: М2эф = {S2, S3, S4, S5, S6, S9, S10}∩{S1, S2, S4, S5, S7, S8, S10} = {S2, S4, S5, S10}. Имеем взаимоприемлемое эффективное решение стейкхолдеров – Мвпэф = {S5}∩{S2, S4, S5, S10} = {S5}.
Приведем заключительный пример также в контексте многопроекционного выбора. Производится поиск компромисса при оценке состояния экономических систем S1–S10 двумя заинтересованными сторонами. Первый стейкхолдер задействует пять проекций (К111–К113, К121–К123, К131–К133, К141–К143 и К151–К153), а второй – две (К211–К213 и К221–К223). Требуется синтезировать общее решение.
Позиция первого стейкхолдера представлена пятью сортированными массивами. Рассмотрим первую проекцию.
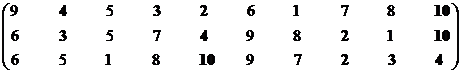
Множество эффективных экономических систем – М11эф = {S2, S3, S4, S7, S10}.
Обратимся ко второй проекции.
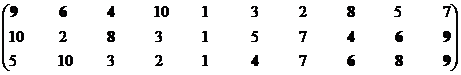
Множество эффективных систем – М12эф = {S4, S6, S7, S8, S9}.
Перейдем к третьей проекции.
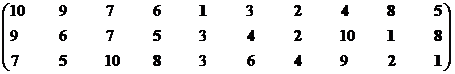
Множество эффективных систем – М13эф = {S1, S2, S4, S5, S8}.
Рассмотрим четвертую проекцию.
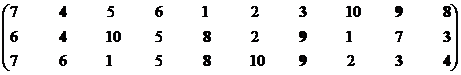
Множество эффективных систем – М14эф = {S3, S4, S8, S9}.
Перейдем к пятой проекции.
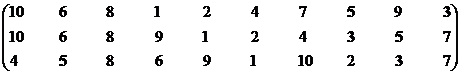
Множество эффективных систем – М15эф = {S3, S5, S7}.
По пяти проекциям эффективное решение первого стейкхолдера не определено – М1эф = {S2, S3, S4, S7, S10}∩{S4, S6, S7, S8, S9}∩{S1, S2, S4, S5, S8}∩{S3, S4, S8, S9}∩{S3, S5, S7} = Ø.
Для достижения компромисса задействуем второй ранг в последней проекции М152р = {S2, S4, S9}, имеем квазиэффективное множество М15кэф = {S2, S3, S4, S5, S7, S9}. Находим асимметричное решение (протоструктуру) М1асим = {S2, S3, S4, S7, S10}∩{S4, S6, S7, S8, S9}∩{S1, S2, S4, S5, S8}∩{S3, S4, S8, S9}∩{S2, S3, S4, S5, S7, S9} = {S4}.
Позиция второго стейкхолдера выражена двумя проекциями. Рассмотрим первую проекцию.
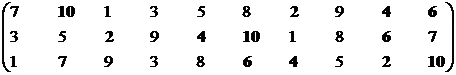
Множество эффективных экономических систем – М21эф = {S2, S4, S6, S7, S10}.
Обратимся ко второй проекции.
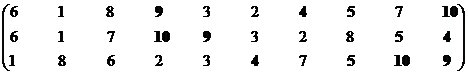
Множество эффективных систем – М22эф = {S4, S5, S9, S10}.
Синтезируем двухпроекционное решение второй стороны: М2эф = {S2, S4, S6, S7, S10}∩{S4, S5, S9, S10} = {S4, S10}. Находим взаимоприемлемое решение стейкхолдеров: Мвпасим = {S4}∩{S4, S10} = {S4}. Далее по аналогии можно получить и сопоставить нижестоящие кластеры. Суть метода ясна.
Заключение
Метод совмещения структур станет ключевым (в том числе связующим) компонентом единой теории и методологии многокритериального и многопроекционного стейкхолдерского выбора и будет востребован при разработке профильных моделей, классификаций, методик и алгоритмов для исследования широкого круга экономических систем на разных уровнях управления при решении актуальных задач анализа устойчивости, безопасности, инновационности и эффективности различными заинтересованными сторонами в лице государств, собственников, менеджеров, инвесторов, кредиторов и иных участников экономических отношений.
Источники:
2. Артемьев Н.В., Лапаев Д.Н., Корнилов Д.А., Митякова Е.В. Инновационное развитие моногородов как императив их экономической безопасности. / Монография. - Нижний Новгород: НГТУ, 2023. – 116 c.
3. Банк С.В., Лапаев Д.Н., Хусаинов М.К. Методы обеспечения экономической безопасности хозяйствующего субъекта от угроз теневой экономики // Russian Journal of Management. – 2024. – № 1. – c. 380–389. – doi: 10.29039/2409-6024-2024-12-1-380-389.
4. Бухвальд Е.М., Лапаев Д.Н. Вариации стратегического планирования и риски для экономической безопасности России // Вестник Нижегородского университета им. Н.И. Лобачевского. Серия: Социальные науки. – 2022. – № 2(66). – c. 7–13. – doi: 10.52452/18115942_2022_2_7.
5. Вакуленко Р.Я., Лапаев Д.Н., Виноградова О.В., Соколов Р.Н. Технологии преодоления экономических санкций. Иранский опыт // Научные исследования и разработки. Экономика фирмы. – 2022. – № 3. – c. 82–90. – doi: 10.12737/2306-627X-2022-11-3-82-90.
6. Кузнецова С.Н., Лапаев Д.Н. Обеспечение комплексной экономической безопасности техно- и промышленных парков // Экономическая безопасность. – 2024. – № 4. – c. 951-966. – doi: 10.18334/ecsec.7.4.120939.
7. Лапаев Д.Н., Лапаева О.Н., Поташник Я.С. Безопасность обрабатывающих производств Владимирской области в экономико-инновационном аспекте // Экономика, предпринимательство и право. – 2023. – № 8. – c. 3005-3018. – doi: 10.18334/epp.13.8.118743.
8. Лапаев Д.Н. Безопасность регионов Приволжского федерального округа в экономико-инновационном аспекте // Экономическая безопасность. – 2023. – № 1. – c. 291-314. – doi: 10.18334/ecsec.6.1.117300.
9. Лапаев Д.Н., Митяков Е.С. Методика многокритериальной оценки экономической безопасности регионов России (на примере Приволжского федерального округа) // Экономика, статистика и информатика. Вестник УМО. – 2013. – № 4. – c. 151–154.
10. Лапаев Д.Н. Методические подходы к анализу и оценке угроз экономической безопасности в социальной сфере // Интернет-журнал Науковедение. – 2016. – № 5 (36). – c. 41.
11. Лапаев Д.Н., Лапаева О.Н. Многокритериальная методика выбора предпочтительных вариантов при сравнении инновационной деятельности отраслей промышленности // Аудит и финансовый анализ. – 2014. – № 5. – c. 113–116.
12. Лапаев Д.Н. Многокритериальное принятие решений в экономике. / Монография, 2-е изд. - Нижний Новгород: НГТУ, 2016. – 281 c.
13. Лапаев Д.Н. Многопроекционная оценка безопасности регионов Приволжского федерального округа в экономико-инновационном аспекте // Экономическая безопасность. – 2024. – № 2. – c. 425-442. – doi: 10.18334/ecsec.7.2.120476.
14. Лапаев Д.Н., Лапаева О.Н., Поташник Я.С. Многопроекционная оценка устойчивости регионов Сибирского федерального округа // Развитие и безопасность. – 2024. – № 2 (22). – c. 90–99.
15. Лапаев Д.Н., Митяков Е.С., Мокрецова Е.С. Мониторинг устойчивого развития отраслей промышленности на основе многокритериального подхода // Экономика, статистика и информатика. Вестник УМО. – 2013. – № 5. – c. 168–171.
16. Лапаев Д.Н., Лапаева О.Н. Принципы выбора многопроекционного решения в экономике // Аудит и финансовый анализ. – 2015. – № 4. – c. 415–417.
17. Лапаев Д.Н., Лапаева О.Н. Формирование методики определения предпочтительных вариантов при сравнении инновационной деятельности отраслей промышленности по совокупности показателей // Аудит и финансовый анализ. – 2014. – № 3. – c. 373–375.
18. Лапаева О.Н., Митякова Е.В. Концептуальная модель обеспечения инновационной деятельности монопрофильных территорий // Развитие и безопасность. – 2022. – № 4 (16). – c. 31–42. – doi: 10.46960/2713-2633_2022_4_31.
19. Лапаева О.Н. Многокритериальная оценка экономического состояния предприятий и отраслей промышленности и выбор предпочтительных альтернатив. / Монография. - Нижний Новгород: НГТУ, 2015. – 145 c.
20. Лапаева О.Н. Многопроекционная оценка состояния промышленных экономических систем. / Монография. - Нижний Новгород: НГТУ, 2018. – 371 c.
21. Лапаева О.Н. Многопроекционная сравнительная оценка альтернатив в экономике. / Монография. - Нижний Новгород: НГТУ, 2017. – 210 c.
22. Лапаева О.Н. Постановка и анализ задач многопроекционного принятия решений в экономике // Гуманизация образования. – 2015. – № 3. – c. 112–116.
23. Лапаева О.Н. Проекционный подход к сравнительной оценке альтернатив в экономике // Современная наука: актуальные проблемы и пути их решения. – 2017. – № 1(32). – c. 41-43.
24. Лапаева О.Н. Принцип ранжированного выбора взаимоприемлемого многопроекционного прогнозного решения // Конкурентоспособность в глобальном мире: экономика, наука, технологии. – 2017. – № 1-1(26). – c. 105–108.
25. Лапаева О.Н. Принцип эффективного выбора взаимоприемлемого многопроекционного прогнозного решения // Конкурентоспособность в глобальном мире: экономика, наука, технологии. – 2017. – № 1-1 (26). – c. 102–104.
26. Митяков С.Н., Лапаев Д.Н., Митяков Е.С., Ладынин А.И. Мониторинг научно-технологической безопасности регионов России: многокритериальный анализ // Инновации. – 2022. – № 3 (281). – c. 18–25. – doi: 10.26310/2071-3010.2022.281.3.003.
27. Митяков С.Н., Лапаев Д.Н., Катаева Л.Ю., Рамазанов С.А. Устойчивое развитие и угрозы экономической безопасности // Экономика и предпринимательство. – 2019. – № 10 (111). – c. 111–114.
28. Морозова Г.А., Мальцев В.А., Мальцев К.В., Лапаев Д.Н. Инновационное развитие промышленных комплексов в регионе. / Монография. - Нижний Новгород: ВВАГС, 2010. – 160 c.
29. митяков С. Н. Экономическая безопасность регионов России. / Монография, 3-е изд. - Нижний Новгород: Нижегород. гос. техн. ун-т им. Р.Е. Алексеева, 2019. – 299 c.
Страница обновлена: 08.10.2024 в 15:43:42