Оптимизация в процессе планирования на уровне государства с использованием межотраслевого баланса

Введение

Переход к проектной экономике невозможен без осуществления оптимального планирования выпуска ключевых отраслей и крупных государственных проектов. Если говорить о коммерческом предприятии, очевидно, что здесь без планирования и прогнозирования невозможна оптимизация деятельности, причем, вектор критериев оптимальности в большинстве случаев заключается в максимизации прибыли за определенный период времени, увеличении доли рынка, поддержании уровня удовлетворенности клиентов качеством товаров и услуг и др. с различными весами [1]. Например, если взять крупное производственное предприятие, то встают следующие вопросы: потратить доступные средства на увеличение производства, либо на капитальные инвестиции, либо же вовсе на исследование рынка и возможную смену вида деятельности.

В случае, когда речь идет об экономике страны, вопрос критерия оптимальности становится острее: может ли это быть увеличение ВВП или доходов бюджета, улучшение благосостояния народа, защита государственной безопасности или обогащение конкретных лиц и фирм (такие случаи нередки)? [2, 3]

Отечественный практический опыт показывает, что зачастую коммерческие предприятия намного эффективнее используют наличные инвестиционные ресурсы, чем государство. Как правило, это связано с тем, что коммерческие фирмы применяют современные технологии и инструменты анализа, прогнозирования и планирования: начиная от громоздких ERP-систем, заканчивая нейронными сетями и математическими инструментами оптимального планирования инвестиционных проектов [4]. Государство зачастую пренебрегает детальными расчетами своих инвест-проектов, несмотря на то, что объемы государственного инвестирования в сотни раз превышают объемы инвестиций коммерческих предприятий, и решения и планы принимаются порой "на глаз". В связи с этим необходимость создания и использования работающих и применимых на практике систем оптимизации и планирования экономики в государственном масштабе приобретает актуальность. [5, 6]

Авторы отмечают, что вопрос об определении адекватного критерия оптимальности выходит за рамки данного исследования, т.к. им, в первую очередь, должно заниматься руководство страны. В данной работе решаются задачи потенциальной возможности оптимизации экономики без проработки идеи об адекватности критерия оптимальности. В связи с этим целю настоящего исследования является разработка метода и инструментария моделирования и оптимизации выпуска отраслей экономики, потому как анализ взаимодействия отраслей экономики или крупных проектов имеет большое значение для формирования управленческих решений. Авторы оставляют открытой возможность программного изменения критериев оптимальности: таких как благосостояние населения, увеличение производства или экспорта и т.д.

Межотраслевой баланс

Методология межотраслевого баланса (МОБ) была разработана В. В. Леонтьевым [7]. МОБ представляет собой экономико-математическую модель, характеризующую межотраслевые производственные и финансовые взаимосвязи в экономике региона или страны.

Данный метод называется балансовым ввиду установления и соблюдения материальных и стоимостных пропорций наличия и источников ресурсов с направлениями и объемами их использования. В данном случае это означает достижение баланса или равенства между производством и потреблением в экономике, что выражается в модели следующей формулой:

(1)

Где - это совокупный выпуск всех отраслей, – технологическая матрица коэффициентов прямых затрат промежуточного потребления, где элементы матрицы - необходимый объем (или доля) продукции -ой отрасли для производства единицы продукции -й отрасли, – совокупное конечное потребление всех отраслей.

Экономико-математическая модель статического МОБ исходит из следующих предпосылок: а) объемы производственного потребления прямо пропорциональны объемам производства продукции потребляющих отраслей, а коэффициентами пропорциональности являются коэффициенты прямых затрат, которые для МОБ в стоимостном выражении определяются как: ; б) каждый продукт производится только одной отраслью.

Коэффициенты прямых затрат – это отраслевые показатели, выражающие непосредственные затраты продукции одной отрасли на производство продукции другой отрасли. Также выделяют коэффициенты полных затрат – это показатели, характеризующие как прямые, так и косвенные затраты одной отрасли на производство продукции другой отрасли, т.е. учитывающие оборот товаров и услуг по всей цепочке технологических связей. Чем интенсивнее связи в экономике, тем выше коэффициенты полных затрат. Эти коэффициенты рассчитываются по следующей формуле:

(2)

Где C – матрица коэффициентов полных затрат, E – единичная матрица

На основе матрицы коэффициентов полных затрат рассчитываются коэффициенты полных потребностей, которые показывают, какой объем валового продукта должен быть произведен при появлении в ней дополнительной потребности у конечного потребителя:

На сегодняшний день существуют базы таблиц «затраты-выпуск», создаваемые Организацией экономического сотрудничества и развития (OECD), включающие симметричные (квадратные таблицы «товар-товар» или «отрасль-отрасль») по 34 отраслям за 1995-2011 гг., а также «Глобальная база таблиц затраты-выпуск» (англ. World Input-Output Database или WIOD) [8], которая составляет стандартизированные межотраслевые таблицы для 43 стран по 56 отраслям.

Практическое применение межотраслевого баланса для прогнозирования и оптимизации функционирования отраслей экономики пришлось на поздний советский период. Большой вклад в развитие межотраслевых моделей внесли советские ученые в 1960-1980 гг., на которые пришелся пик их разработок. Множество работ, посвященных статическому и динамическому межотраслевому балансу было сделано В. Коссовым [9], А. Г. Гранбергом [10, 11].

В работах А. Г. Гранберга и др. [10, 11] обобщены результаты исследований разработанных авторами модельных комплексов СИРЕНА и СИРЕНА-2, являющихся плодом труда нескольких десятилетий ученых СО РАН, которые предназначены для оценки направлений и приоритетов региональной инвестиционной политики.

Обширная работа была сделана учеными под руководством В. Ильина [12]. Также можно отметить работы Баранова [13, 14]. Среди современных ученых, необходимо отметить работы В. Л. Макарова [15], в которых автор рассматривает возможность использования механизма стратегического планирования применительно к российским условиям и предлагает модель проектной экономики, представляющую собой компьютерный инструмент для составления и реализации стратегического планирования страны, а также совместную работу автора данной статьи Ахмадеева Б. А. и Макарова В. Л. [16], в которой описывается механизм оптимизации экономических проектов, основанный на методе численной оптимизации. Также нельзя не отметить работы по анализу и оптимизации межотраслевого баланса среды зарубежных ученых. [17, 18]

Модель оптимального планирования (ОП), основана на инструментарии математического программирования. Основоположником данной идеи является Л. В. Канторович, [19]. Принцип оптимального планирования в комбинации с методом экономического анализа, основанном на таблицах затраты-выпуск является мощнейшим инструментом для анализа состояния экономики и дальнейшего планирования экономической деятельности. [20, 21]

В общем виде задача представляет собой стандартную оптимизационную задачу, которая называется обычно прямой:

(3)

Где - вектор коэффициентов оптимальности (например, им может быть прибыль), – вектор объемов (интенсивности) выпуска продукции отраслей (или т.н. способов производства), - производственная матрица, где положительные значения обозначают выпуск продукции, а отрицательные – потребление, – вектор ограничений на ресурсы. Стоит отметить, что технологическая матрица в формуле (1) отличается от производественной матрицы в формуле (3) тем, что в первом случае это коэффициенты прямых затрат, а не конечное стоимостное или конечное выражение выпуска продукции определенной отрасли.

Также определяется двойственная к прямой задача оптимизации. Ее решение означает нахождение т.н. объективно-обусловленных оценок (о.о. оценки) на каждый из ресурсов (столбцы в матрице ). В классической оптимизационной проблеме решение двойственной задачи означает нахождение оценок на ресурсы, указанные в ограничениях (вектор ), при продаже которых мы бы получили доход не меньше того, который образуется в случае использовании ресурсов для производства нашими способами, т.е. той самой прибыли, указанной в векторе . Двойственная к задаче (3) формулируется следующим образом:

(4)

Где – вектор ресурсов, – производственная матрица, – оценки ресурсов.

Математический смысл данных оценок заключается в том, что они определяют, на сколько увеличится (уменьшится) значение целевой функции при увеличении (уменьшении) запаса данного ресурса на одну единицу.

Алгоритм преобразования таблицы затраты-выпуск в задачу оптимизации

В качестве источника статистических данных была выбрана база данных WIOD [8]. Данные в таблицах приведены в текущих ценах. Приведем пример структуры симметричной таблицы «отрасль-отрасль» за 2000 год по экономике России (Таблица 1).

Таблица 1.

Схематичный пример таблицы межотраслевого баланса по РФ за 2000 год. (Источник: WIOD [8])

Опишем алгоритм преобразования таблицы МОБ в задачу линейной оптимизации:

1) Сложение двух подматриц: промежуточного потребления и структуры импорта для промежуточного потребления:

(5)

Где – подматрица промежуточного потребления, – подматрица импорта для промежуточного потребления. В данном случае мы предполагаем, что импортируемый товар также выпускается отечественными отраслями, поскольку целью настоящего исследования является перераспределение интенсивностей выпуска по определенным категориям товаров и услуг без разделения на импортные и отечественные.

2) Подсчет суммы производства по каждой отрасли за вычетом того объема, который она производит для самой себя:

(6)

Где – количество отраслей, – сумма промежуточного и конечного потребления –ой отрасли, – объем производства –ой отрасли для самой себя.

3) Замена положительных значений для всех недиагональных элементов матрицы на отрицательные (затраты производственного способа)

(7)

4) Присвоение суммы (6) значению производства отрасли для самой себя (выпуск производственного способа):

(8)

5) Транспонирование матрицы =

Далее вводится новый ресурс, который обозначен центральным банком (“Bank”), средства которого будут ограничены в объеме, сопоставимом с объемом затрат общего выпуска продукции исследуемой экономики.

Таблица 2.

Преобразованная таблица затраты-выпуск (Источник: составлено авторами на основе таблиц WIOD [8])

В приведенном примере оптимизационной задачи (Таблица 2) ограничение задано суммарным объемом затрат всех отраслей. Центральный банк посредством финансовых инвестиций в каждую отрасль, может стимулировать или дестимулировать выпуск любой отрасли, а сама отрасль при этом тратит из общего объема сумму затрат на собственное производство пропорционально своим затратам из базовых данных. Для всех остальных ресурсов ограничения заданы через ноль – т.е. объем производства каждого ресурса равен объему потребления этого ресурса. Соответственно, сумма производства-потребления каждого товара (по столбцам), зависящего от интенсивности применения каждого способа должна быть не меньше нуля. Это означает, что мы не можем потребить больше, чем произвели. То же касается и ЦБ – он не может выдать денег больше, чем имеет в качестве ограниченного ресурса. В данном примере это сделано для того, чтобы посмотреть, каким образом можно оптимизировать интенсивность работы отраслей при имеющихся ресурсах, без введения дополнительных

Из соответствующей таблицы видно, что, в качестве критерия оптимальности (последний столбец) было выбрано конечное потребление домохозяйствами со значением равным единице (“final consumption expenditure by households”).

Ниже математически описан пример задачи, приведенный в таблице 2:

(9)

Где значения – обозначают интенсивность выполнения каждого способа производства. Это означает, что каждый вектор-строка в приложении 2 умножается на значение соответствующей интенсивности, где – множитель для первого способа – множитель для второго способа и т.д.

Решение задачи (9) получено с использованием системы Wolfram Mathematica (Таблица 3) цветом выделены значения решения прямой (x) и двойственной (y) задач.

Таблица 3.

Решение прямой и двойственной задачи линейного программирования (Источник: составлено авторами на основе таблиц WIOD [8])

Серым цветом выделены столбец со значениями интенсивности оптимального использования отраслей (x) и строка со значениями дефицитности (y) различных продуктов (о.о. оценки). Используя описанный выше алгоритм, перейдем далее к оптимизации отраслей на полных таблицах затраты-выпуск.

Отраслевая оптимизация экономики на основе полных таблиц затраты-выпуск

Проведем оптимизацию с максимизацией конечного потребления для данных МОБ с использованием алгоритма, описанного выше. Оценим, как с течением времени менялось значение конечного потребления отраслей – оптимален ли был объем выпуска каждой отрасли согласно нашей задаче.

Коэффициент корреляции между структурой затрат отраслей соседних лет достаточно высокий – минимальное значение на уровне 0,86, а корреляция между годами 2010-2011 и 2013-2014 близка к единице. Это говорит в целом о неизменной структуре затрат.

Далее проведем оптимизационный эксперимент с максимизацией конечного потребления, где сравним, как значения индекса роста оптимальной интенсивности применения отраслей согласно решению оптимизационной задачи (2010 г.) соотносятся с реальными значениями индекса роста конечного потребления за следующий за оптимизируемым период (2011 г.):

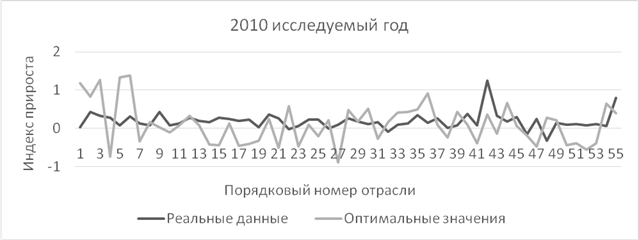
Рис. 1. Графики индексов прироста конечного потребления (Источник: составлено авторами на основе WIOD [8])

На графике на рис. 1 видно, что реальные данные редко совпадают с оптимальными. Из этого можно сделать вывод о потенциальной возможности оптимизировать выпуск отраслей на следующий год. Далее в таблице 4 мы доказываем, что конечное потребление по оптимальному плану всегда выше реального с учетом скорректированных значений реального конечного потребления по всем отраслям на валовый выпуск.

Таблица 4

Значения объемов скорректированного и оптимизированного конечного потребления (млн. руб.) (Источник: составлено авторами на основе WIOD [8])

Отметим, что коэффициент корреляции между структурой конечного потребления соседних лет в исследуемом периоде достаточно высок: 2010-2011: 0,997, 2011-2012: 0,961, 2012-2013: 0,938, 2013-2014: 0,998, что так же говорит в целом о неизменной структуре потребительского спроса.

Очевидно, что линейные производственные функции отраслей, представленные в таблицах затраты-выпуск, не являются точными. Тем не менее, представленная оптимизация может дать направления по регулированию объемов выпуска в каждой из отраслей, поскольку в первом приближении любую нелинейную функцию можно сгладить линейной.

Приведем примеры отраслей за 2010 г., индекс прироста которых на основании решения оптимизационной задачи оказался выше 0,5, т.е. те отрасли, увеличение выпуска которых даст наибольший прирост конечного потребления в следующем году при неизменной структуре потребления:

Таблица 5

Отрасли с индексом прироста > 0,5 (Источник: составлено авторами на основе WIOD [8])

Теперь приведем примеры отраслей за 2010 г., c наибольшим отрицательным индексом прироста (< -0,5), инвестиции в которые наименее эффективны с точки зрения критерия оптимальности:

Таблица 6

Отрасли с индексом прироста < -0,5 (Источник: составлено авторами на основе WIOD [8])

Мы видим по результатам в таблице 3, что согласно решению оптимизационной задачи, рекомендуется сократить издержки на образование на 56%. Уменьшая расходы на образование, даже если это оптимально с точки зрения тактического увеличения производства товаров, через 5-10 лет может сказаться на том, что производить товары будет некому.

Проведем эксперимент с максимизацией выпуска отрасли «образование» на данных за 2010 г., установив критерий оптимальности напротив этой области, равный 1, а также, задав условие, что уровень интенсивности способа «конечное потребление» должен быть не меньше 1, т.е. не меньше прошлогоднего уровня. На рис. 2 для сравнения представлены индексы прироста при различных критериях оптимальности:

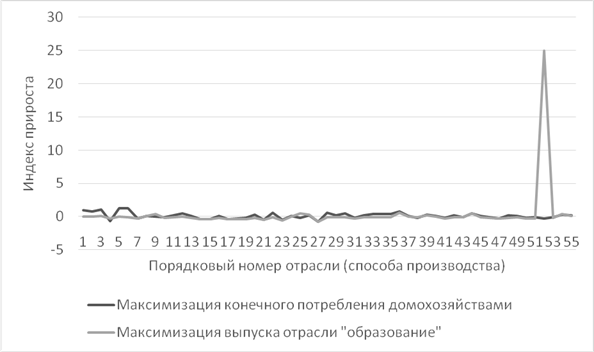
Рис. 2. Оптимальные индексы прироста отраслей (Источник: составлено авторами)

Выведем результаты наиболее перспективных и наименее значимых отраслей, согласно новой постановке задачи в табл. 7 и 8:

Таблица 7

Отрасли с индексом прироста >0,5 (Источник: составлено авторами на основе WIOD [8])

Таблица 8

Отрасли с индексом прироста < -0,5 (Источник: составлено авторами на основе WIOD [8])

Из таблиц 7 и 8 видно, что при задаче максимизации выпуска отрасли «образование» рекомендации по увеличению или уменьшению финансирования различных отраслей совершенно отличаются от предыдущей задачи.

Проследим далее динамику изменения дефицитности денежных ресурсов (двойственных оценок) с максимизацией выпуска отрасли «образование» и конечного потребления на рис. 3 и 4 соответственно:

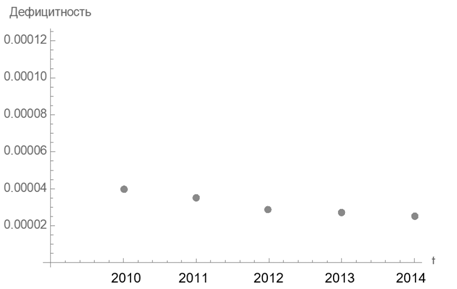
Рис. 3. Дефицитность денежных ресурсов с 2010 по 2014 гг. для максимизации выпуска отрасли «образования» (Источник: составлено авторами на основе WIOD [8])

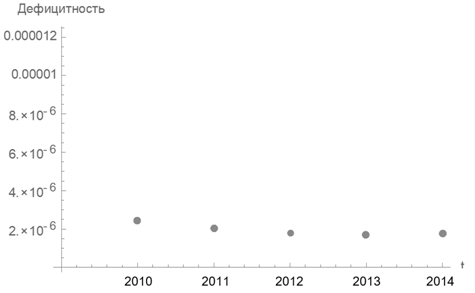
Рис. 4. Дефицитность денежных ресурсов с 2010 по 2014 гг. для максимизации конечного потребления. (Источник: составлено авторами на основе WIOD [8])

Исходя из двойственных оценок ресурса «Банк», структура изменения дефицитности данного ресурса с 2010 по 2014 гг. сохраняется неизменной как как для задачи оптимизации выпуска с максимизацией отрасли «образование», так и для задачи с максимизацией конечного потребления. Однако, как свидетельствуют значения из графиков на рис. 3 и 4, денежный ресурс является более дефицитным при задаче максимизации выпуска отрасли «образование».

Заключение

В статье был приведен и подробно описан авторский алгоритм преобразования симметричной таблицы МОБ на базе статистических данных, предоставленных Всемирной базой данных таблиц затраты-выпуск (WIOD), в задачу линейной оптимизации. Было показано, что структура потребления отраслей, а также конечного потребления не менялась значительно в рамках исследуемого периода (2010-2014 гг.), что говорит о возможности использования таблицы за определенный год для прогнозирования и оптимизации экономики на ближайшие несколько лет. Был приведен пример оптимизации отраслей с разными критериями оптимизации – максимизацией конечного потребления и максимизацией выпуска отрасли «образование». Показано, как критерий оптимизации влияет на решение оптимизационной задачи, а также на дефицитность различных ресурсов: нехватка денежных ресурсов стоит более остро при задаче максимизации выпуска отрасли «образование», чем при задаче максимизации конечного потребления.

Очевидно, что качество результатов данной оптимизации самым главным образом зависит от истинности предоставленных данных. Тем не менее, как уже было сказано выше, целью работы являлось создание инструментария. Также отметим, что для того, чтобы формировать управленческие решения на основе результатов оптимизации, необходимо дальнейшее исследование результатов, анализ и сравнение внутреннего выпуска с импортом, а также их качественный анализ, что планируется сделать в последующих работах авторов.