Подходы к построению предсказательных моделей логистических процессов

Введение

В современном мире основной проблемой прогнозирования событий, в частности логистических процессов, является тот факт, что объем информации в логистических системах растет быстрыми темпами, причем как в объемах, так и в разновидностях форматов данных. В эту эпоху активного информационного развития перед аналитиками и учеными возникает острая необходимость создания новых методов моделирования, которые могут удовлетворять потребностям эффективности логистического процесса, как внутри предприятия, так и в цепочках поставок в целом.

Объектом исследования в данной работе являются существующие подходы и методы предсказательного моделирования, применяемые к логистическим процессам.

Целью работы является систематизация моделей и методов, позволяющих использовать их в качестве предсказательных по отношению к логистическим процессам.

Методология – кабинетные исследования, сравнительный анализ.

Методический аппарат исследования включает в себя метод кабинетного исследования для изучения информации в книгах и научных статьях о существующих подходах и методах моделирования, применяемых к логистическим процессам, а также метод сравнительного анализа для сопоставления полученной информации и составления сравнительной таблицы.

Новизна работы заключается в том, что при наличии различных подходов и методов моделирования логистических процессов нет систематизированного списка, отражающего основные их характеристики, который можно использовать для выбора подходящего метода для своей компании в той или иной ситуации.

Авторская гипотеза состоит в том, что на сегодняшний день, несмотря на существование множества различных подходов и методов моделирования логистических процессов, нет такого, который бы идеально подходил для логистических систем в любой компании и цепочки поставок в целом.

Литературный обзор

Предсказательной аналитикой, которую называют также прогнозной или предиктивной, называется класс методов анализа данных, концентрирующийся на прогнозировании будущего поведения объектов и субъектов с целью принятия оптимальных решений [1] (Sigel, 2014).

Благодаря активному развитию информационных и компьютерных технологий системы прогнозного анализа используются в различных областях, позволяя реализацию математических методов обработки больших объемов данных [2] (Shcherbatov, 2019). Прогнозное моделирование с использованием нейронных сетей и машинного обучения с применением высокоскоростной обработки данных и параллельных вычислений можно считать одним из перспективных направлений предиктивной аналитики [3] (Bruskin, 2018).

В современной предсказательной аналитике используются так называемые метамодели, или суррогатные модели, которые «обучаются» по множеству прототипов входных и выходных данных и имитируют (заменяют) как источники получения данных, так и сами модели [4] (Burnaev, 2019).

Наряду с другими отраслями активно развивается применение предиктивной аналитики в области управления цепями поставок для прогнозирования спроса, планирования производства, запасов, дистрибуции, ценообразования, послепродажного обслуживания, то есть на всех этапах цепи [5].

Понятие «логистический процесс» можно рассматривать как в широком, так и в узком смысле.

Если говорить о широком понимании логистического процесса, то он представляет собой совокупность логистических операций и определяется как организованная во времени и пространстве последовательность выполнения операций, которая подчинена достижению целей хозяйственной системы с применением принципов и методов логистики [6] (Golikov, 1999).

В определении логистического процесса как упорядоченной на оси времени последовательности логистических операций, направленной на обеспечение потребителей продукцией соответствующего ассортимента и качества в нужном количестве в требуемое время и место [7] (Rodnikov, 2011), также прослеживается представление логистического процесса как множества взаимосвязанных логистических операций.

В случае же рассмотрения логистического процесса в более узком понимании его можно приравнять к понятию логистической операции [8] (Toluev, 2005).

Логистические процессы имеют место не только в торговых и транспортных предприятиях или складских объектах, которые традиционно принято считать логистическими, но и в любых других областях, где наблюдается движение большого количества материальных объектов [8] (Toluev, 2005).

Для построения системы предсказательной аналитики могут быть использованы различные подходы, методы и модели, которые будут рассмотрены в данной работе.

Дерево решений – метод, который применяется при необходимости принятия последовательного ряда решений в условиях риска. Дерево решений позволяет увязать точки принятия решения, возможные стратегии и их последствия с учетом влияния факторов среды. Дерево решений отображает возможные действия и их последствия, а его конечной целью является создание модели, предсказывающей значение целевой переменной на основе нескольких переменных на входе [9] (Trofimova, Trofimov, 2012).

Метод деревьев решений является одним из наиболее популярных методов решения задач классификации и прогнозирования. Деревья решений применяются для представления правил, имеющих логическую структуру «если…, то …», в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение [10] (Yakovlev, Seredin, 2018).

Цепи Маркова – стохастическая модель, описывающая последовательность возможных событий, в которой вероятность каждого события зависит только от состояния, достигнутого в предыдущем событии [11] (Stivenson, Ueyt, 2011).

Марковские цепи с заданным интервалом времени и начальным распределением, с последующим расчетом будущего состояния применяются к сериям зависимых случайных величин [12] (Tyan, Rakhmangulov, Muravyov, Van, 2018).

Теория игр – это математическая теория стратегии, которая предполагает существование по меньшей мере двух игроков, выбор которых определяет исход. Конфликт игроков, связанный с противоречивыми предпочтениями, в рамках данной теории может быть частичным, когда оба игрока могут быть в выигрыше или же, напротив, в проигрыше. В основе теории игр – стратегии игроков, которые находятся в равновесии [13] (Neyman, Morgenshtern, 1970).

Модели теории игр могут быть применены и к экономике, так как интересы участников экономических процессов могут не совпадать, и даже быть конфликтными, и каждый игрок решает свою локальную задачу, пытаясь максимизировать свою собственную прибыль. В результате система приходит в какое-то равновесное состояние. С помощью равновесной ситуации можно определить оптимальное решение игры [14] (Ganicheva, Ganichev, 2019).

Системная динамика – модель, в рамках которой процессы, происходящие в мире, представляются в виде накопителей и потоков между ними. Такая модель описывает структуру и поведение системы посредством множества взаимодействующих связей и задержек, и в качестве результата выявляет и показывает зависимости и причинно-следственные связи моделируемой системы [15, 16] (Shterman, 2000; Skorodumov, 2015).

Системная динамика позволяет описывать сложные системы естественным образом, минимизируя математические расчеты, что делает ее своеобразным прорывом в моделировании сложных систем [17] (Tregubov, Slavnetskova, 2020).

В настоящее время системная динамика широко распространена и ее методы применяются в различных сферах – экологической политике, городском планировании, экономической политике, транспортных технологиях и многих других [17] (Tregubov, Slavnetskova, 2020).

Дискретно-событийное моделирование представляет систему в виде хронологической последовательности событий, происходящих в определенный момент времени и являющихся показателями изменения системы – продвижение по модели происходит либо от события к событию, либо через дискретные промежутки времени [16, 18] (Skorodumov, 2015; Lou, Kelton, 2000).

Дискретно-событийное моделирование сосредоточено на описании процессов, которые описываются как дискретные потоки событий. Значимыми считаются события, которые вносят в характер течения процесса значимые изменения и образуют дискретный поток значимых событий, а незначимые события остаются за рамками модельной абстракции [19] (Ramazanov, 2017).

Агентное моделирование – подход, основной идеей которого является получении представления о глобальных правилах функционирования всей системы, исходя из индивидуального поведения ее отдельных активных объектов и их взаимодействия [16] (Skorodumov, 2015).

Агентная модель состоит из множества индивидуальных агентов и их окружения. Каждый агент может взаимодействовать как с другими агентами, так и с внешней средой и может изменять свое поведение и внешнюю среду в процессе функционирования [20] (Gaykova, 2019).

В агентном моделировании применяется принцип репрезентации объектов «снизу-вверх», то есть акцент делается не на макро-, а на микроуровень, когда правила поведения задаются для каждого из агентов, которыми могут быть любые автономные сущности из реального мира, взятые в интересующей исследователя системе отношений, а общая динамика системы является следствием совокупности взаимодействий этих агентов [19] (Ramazanov, 2017).

Анализ выживаемости представляет собой набор статистических процедур для анализа данных, в которых интересующей переменной результата является время до события [21] (Klyaynbaum, Klyayn, 2012).

Анализ выживаемости является одним из самых распространенных методов статистического анализа в медицине [22] (Zulkarnaev, 2019).

Несмотря на то, что данный подход к моделированию чаще всего используется в области медицины и изначально применялся для оценки продолжительности жизни пациентов при изучении эффективности методов лечения, на сегодняшний день анализ выживаемости применяется и во многих других отраслях [21] (Klyaynbaum, Klyayn, 2012).

Основные результаты

Глобальная и ключевая цель моделирования заключается в прогнозировании поведения процесса или системы. В зависимости от того, насколько точно и в полной мере модель отображает моделируемый объект, модели подразделяются на изоморфные и гомоморфные [23, 24] (Gadzhinskiy, 2012; Melnikov, Skhirtladze, Antonyuk, 2015) (рис. 1).

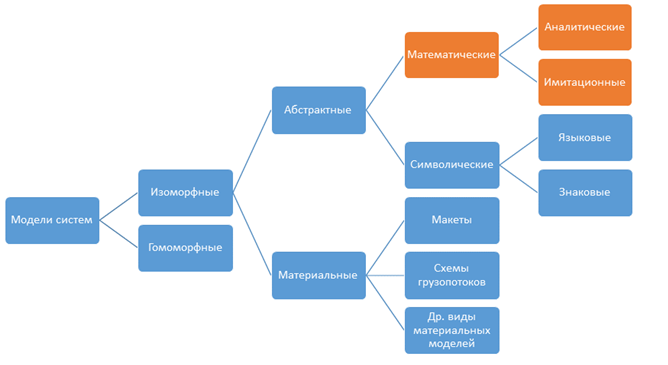
Рисунок 1. Классификация моделей логистических систем

Источник: составлено авторами на основе данных из источников [23, 24] (Gadzhinskiy, 2012; Melnikov, Skhirtladze, Antonyuk, 2015).

Изоморфные модели – это модели, которые максимально точно отображают моделируемые объекты (процессы, системы), их характеристики, особенности и могут быть эквивалентной их заменой [23, 24] (Gadzhinskiy, 2012; Melnikov, Skhirtladze, Antonyuk, 2015).

Гомоморфные модели отображают моделируемый процесс частично, допуская не принимать во внимание абсолютно все характеристики объекта и влияющие факторы. Несмотря на меньшую точность, данная разновидность моделей является более применимой к логистическим процессам, так как построение изоморфной модели является практически невозможным из‑за огромного множества факторов, оказывающих на них влияние. Также гомоморфные модели являются более простыми и универсальными в построении и применении [23, 24] (Gadzhinskiy, 2012; Melnikov, Skhirtladze, Antonyuk, 2015).

В свою очередь, гомоморфные модели в зависимости от степени материальности делятся на материальные и абстрактные. Материальные модели предполагают воспроизведение функциональных, физических, геометрических и динамических характеристик моделируемого объекта и являются весьма дорогостоящими, в связи с чем большей популярностью и применением в логистике пользуются именно абстрактные модели [23, 24] (Gadzhinskiy, 2012; Melnikov, Skhirtladze, Antonyuk, 2015).

Среди абстрактных моделей можно выделить символические и математические. Наиболее широко применяются в логистике именно математические модели таких разновидностей, как аналитические и имитационные, которые мы рассмотрим более подробно [23, 24] (Gadzhinskiy, 2012; Melnikov, Skhirtladze, Antonyuk, 2015).

Аналитическое моделирование – это математический подход к исследованию логистических систем, целью которого является получение максимально точных решений. В процессе моделирования с использованием данного подхода необходимо выполнение следующих этапов [25] (Nikolaychuk, 2017):

1. Формулировка математических законов, связывающих объекты моделируемой системы, в виде алгебраических, дифференциальных и других функциональных соотношений.

2. Решение уравнений с возможным использованием вычислительной техники и получение теоретических результатов.

3. Проверка полученных теоретических результатов и сопоставление их с практикой [25] (Nikolaychuk, 2017) (рис. 2).

Рисунок 2. Процесс аналитического моделирования

Источник: составлено авторами на основе данных из источников [23, 24] (Gadzhinskiy, 2012; Melnikov, Skhirtladze, Antonyuk, 2015).

Имитационное моделирование предполагает проведение экспериментов с математической моделью, которая описывает поведение системы в течение определенных периодов времени, с использованием информационных технологий. В случае применения данного вида моделирования логистических процессов закономерности, определяющие характер количественных отношений внутри этих процессов, остаются неопознанными (метод «черного ящика») – экспериментатор может лишь менять условия протекания процесса и наблюдать получаемый результат. Конечной целью имитационной модели является определение таких оптимальных условий, при которых результат будет максимально удовлетворять заявленным требованиям [23, 3] (Gadzhinskiy, 2012; Bruskin, 2018).

Имитационное моделирование обычно проводится в два этапа [25] (Nikolaychuk, 2017):

1. Конструирование модели реальной логистической системы.

2. Проведение экспериментов на данной модели (рис. 3).

Рисунок 3. Процесс имитационного моделирования

Источник: составлено авторами на основе данных из источников [23, 24] (Gadzhinskiy, 2012; Melnikov, Skhirtladze, Antonyuk, 2015).

Для определения наиболее подходящего вида моделирования, применимого к логистическим процессам, авторами составлена сравнительная таблица, в которой представлены их основные преимущества и недостатки (табл. 1).

Таблица 1

Сравнение аналитического и имитационного моделирования логистических процессов

В связи с тем, что логистические системы функционируют в условиях неопределенности окружающей среды и подвергаются воздействию множества факторов, в том числе имеющих случайный характер, имитационное моделирование, учитывая его способность учитывать подобные факторы, может более точно спрогнозировать сценарии протекания логистических процессов. Но стоит также учитывать и определенные недостатки данного метода, такие как высокая стоимость и невозможность масштабирования [23, 25] (Gadzhinskiy, 2012; Nikolaychuk, 2017).

Помимо сравнения аналитического и имитационного моделирования логистических процессов рассмотрим также и конкретные наиболее популярные подходы и теории (табл. 2).

Таблица 2

Подходы к моделированию логистических процессов

В конечном итоге можно увидеть, что на сегодняшний день существует множество методов и моделей, также и кроме описанных в данной статье, которые так или иначе могут быть применены к моделированию логистических процессов. Каждый подход имеет свои особенности, преимущества и недостатки, и на данный момент не существует такого метода, который бы идеально подходил для моделирования логистических систем и процессов.

На основе проведенного анализа можно сказать о том, что идеальной для моделирования логистических процессов будет такая модель, которая будет включать в себя преимущества и исключать недостатки всех рассмотренных подходов и методов, а именно:

· Надежность и безопасность.

· Отсутствие высоких требований к подготовке данных.

· Простота построения, настройки и использования.

· Простота в понимании и интерпретации результатов моделирования.

· Единообразие анализа и проектирования.

· Работа с большими объемами данных без необходимости наличия дополнительного специального оборудования.

· Возможность представления проблемы с точки зрения конкурентов.

· Интерпретируемость системных потоковых диаграмм.

· Учет изменений во времени параметров системы и внешней среды.

· Учет субъективных предпочтений и опыта эксперта в процессе принятия решений.

· Возможность анализа результатов на каждом этапе.

· Простота сопровождения.

· Работа с цензурированными данными.

· Полнота представления данных.

· Оптимальность принятия решения в рамках всей системы.

· Моделирование процессов с длинной памятью.

· Широкое применение моделей.

· Прогнозирование результата с учетом хаотичного поведения субъектов модели.

· Учет качественных изменений системы.

· Учет возникновения непредвиденных обстоятельств.

· Учет непрерывности процесса и взаимозависимости элементов системы.

Логистическая система в любой компании должна быть построена таким образом, чтобы соблюдать главное правило логистики – правило «7R», которое в некоторых источниках называется логистическим миксом и заключается в обеспечении наличия необходимого товара определенного качества в необходимом количестве своевременно и в нужном местоположении конкретному потребителю с требуемым уровнем затрат [26] (Moiseeva, 2008).

И несомненно, идеальная модель логистических процессов помимо обладания перечисленными преимуществами должна иметь своей обязательной и ключевой целью соблюдение правила логистики «7R». Перечисленные элементы и характеристики идеальной модели представлены на рисунке 4.

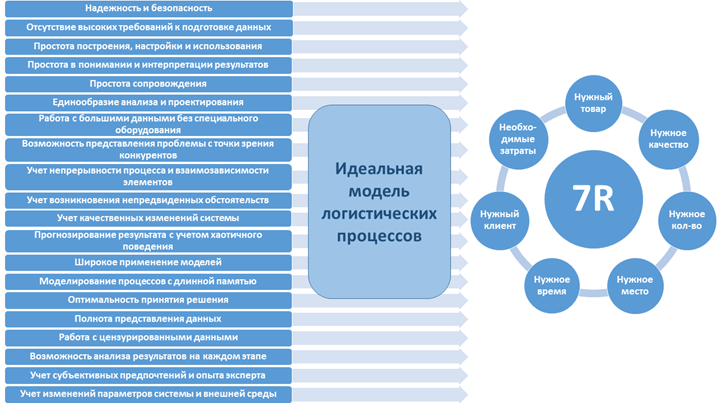
Рисунок 4. Идеальная модель логистических процессов

Источник: составлено авторами на основе проведенного в данной работе исследования.

На сегодняшний день идеальной модели с указанными признаками не существует, но учитывая активное развитие искусственного интеллекта, машинного обучения и методов обработки больших данных за последние несколько лет, создание такой модели возможно в ближайшем будущем.

Заключение

В результате проведенного исследования были изучены основные разновидности моделирования процессов, а также наиболее популярные подходы, методы и модели, применяемые при моделировании логистических процессов, систематизированы знания и классификация данных методов и моделей, выявлены их основные преимущества и недостатки. На основе полученных знаний разработаны требования, которым должна соответствовать будущая идеальная модель логистических процессов. Она должна включать все преимущества имеющихся методов и подходов, не иметь описанных недостатков и своей главной целью иметь соблюдение основного правила логистики «7R».

Обобщенное описание существующих подходов к моделированию процессов поможет авторам, осуществляющим дальнейшие исследования в данной области, и может быть использовано в качестве выбора подходящего метода моделирования.

Проблемой, выявленной в ходе работы, является отсутствие на данный момент метода моделирования, который бы идеально подходил для применения ко всем логистическим процессам и отвечал всем имеющимся требованиям.

Авторы в качестве решения данной проблемы предлагают перечень требований, которые должна включать идеальная модель, который может быть использован учеными для ее дальнейшей разработки.

Возможные направления дальнейших исследований лежат в плоскости создания на основе предложенных требований и характеристик, полученных в ходе исследования, идеального метода моделирования логистических процессов учеными в области разработки имитационных и аналитических моделей с использованием больших данных, искусственного интеллекта и машинного обучения и реализации описанной модели.