Оценка курсовой стоимости ценных бумаг

1. Математический аппарат вычисления курсовой стоимости ценных бумаг

Одним из показателей, который определяется в ходе фундаментального анализа, является дисконтированная стоимость будущих доходов (Р_диск), получаемых в результате инвестирования денежных средств в ценные бумаги. По этому показателю производится оценка курсовой стоимости ценных бумаг (прежде всего облигаций и акций) и делается вывод о том, соответствует ли рыночная цена финансового инструмента тем доходам, которые можно получить с его помощью; переоценен он или недооценен; следует его продавать или покупать.

В условиях рыночной экономики инвестирование всегда связано с риском неполучения запланированного дохода (риском недостижения поставленной в ходе инвестирования цели). Причем, чем на большую доходность рассчитывает инвестор, тем большему риску он подвергается (рис. 1).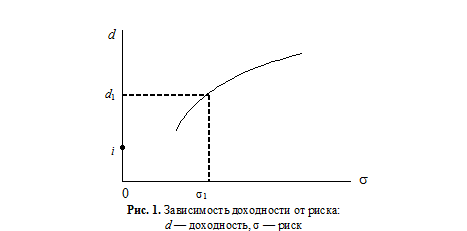

Когда возникает вопрос о том, куда (в какой финансовый инструмент) вложить деньги, вариантов, как правило, бывает много:

‑ на депозит в банк под процент;

‑ в недвижимость;

‑ в драгоценности;

‑ в произведения искусства;

‑ в ценные бумаги (государственные или корпоративные) и т.д.

Каждый из вариантов способен обеспечить определенную доходность вложений при соответствующем риске.

Доходность самых надежных вложений (рис. 1) можно считать своеобразной точкой отсчета — базовой ставкой процента (i). Эту доходность называют еще нормой прироста капитала, или ставкой дисконта. Это практически безрисковый процент, который в странах со стабильной рыночной экономикой могут обеспечить государственные краткосрочные облигации. Все другие вложения денежных средств сопряжены с большим риском, но позволяют получить более высокую доходность.

Инвестиции всегда увязывают с конкретным периодом времени (Т_и). И это не случайно. Фактор времени в финансовых операциях имеет исключительно важное значение. “Время — деньги”. Дело в том, что деньги, вложенные под проценты, способны приносить доход. Этот доход зависит от периода Т_и, на который осуществляются инвестиции. То есть ДЕНЬГИ ИМЕЮТ ВРЕМЕННУЮ СТОИМОСТЬ!

Как же оценить будущую стоимость сегодняшних денег?

Предположим, исходная денежная сумма Р вкладывается в инвестиционный проект на n периодов времени (Т_и = n) под r процентов за соответствующий период. Чаще всего в качестве единичного периода времени берется год. И r при этом является ставкой годовых процентов. Какой же будет стоимость сегодняшних денег через n периодов времени? Обозначим эту будущую стоимость символом F.

Существуют два основных подхода к оценке F [1(2)]:

а) финансовые вычисления на основе простых процентов;

б) финансовые вычисления на основе сложных процентов.

Целесообразно рассмотреть каждый из этих подходов более детально.

При финансовых вычислениях на основе простых процентов исходная сумма денег на начало каждого периода инвестиций остается неизменной.

Через один период времени (например, через год) стоимость денежных средств будет (в данном выражении r берется в долях единицы). На второй период (на второй год) в инвестиционный проект снова вкладывается сумма P (а доход в размере Pr изымается из оборота).

Через два периода инвестиций (два года) На очередной период в инвестиционный проект снова будет вложена сумма Р (а доход в размере 2Pr изъят из оборота). И так далее.

Через n инвестиционных периодов (n лет)

При финансовых вычислениях на основе сложных процентов исходная сумма денег на начало каждого следующего периода инвестирования меняется. Дело в том, что полученный в ходе текущего периода доход не изымается из оборота, а реинвестируется (добавляется к исходной сумме и совместно с ней вкладывается под проценты). Или, как говорят, идет начисление процентов на проценты. При этом: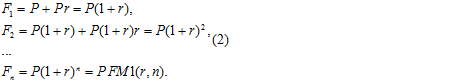

Сомножитель обычно называют коэффициентом наращения, или процентным фактором будущей стоимости FM1(r, n). Значения этого факторного множителя табулированы, что существенно упрощает процессы вычисления [1(2)].

Следует отметить, что при малой ставке процента (единицы процента) результаты вычислений для простого и сложного процентов различаются мало. При ставке процента 10 и более отличия существенны.

Обычно при малых сроках инвестирования (не более одного года) используют вычисления на основе простых процентов. При инвестировании на более длительные сроки вычисления производят на основе сложных процентов.

Полученные выражения для будущей стоимости денег можно интерпретировать следующим образом: сегодняшняя сумма денег Р эквивалентна сумме денег F в будущем (с точки зрения и покупательной способности, и потребительской стоимости денег, и возможных рисков). Так как F больше P, значит для решения тех же задач в будущем потребуется больше денег.

То есть деньги с течением времени дешевеют. Отсюда вытекают два важных правила эккаунтинга (account):

1) сегодняшняя стоимость денег не равна их завтрашней стоимости (рубль, полученный сегодня, стоит дороже рубля, который будет получен завтра);

2) деньги, полученные в разные периоды времени, нельзя просто складывать. Это разные деньги.

Как же сравнивать деньги, полученные в разные периоды времени? Как посчитать общую сумму дохода, полученного в разные периоды времени?

Для решения этих задач доходы разных периодов пересчитывают на одну дату (чаще всего на момент начала инвестирования, определяя современную стоимость будущих доходов). Такой пересчет называют дисконтированием.

Пусть F — денежная сумма, гарантируемая инвестиционным проектом через n периодов времени (например, n лет). Какова ее сегодняшняя стоимость, если r — процентная ставка (ставка дисконта)? Пересчет можно осуществить, используя выражение (2):

где P — сегодняшняя стоимость будущих доходов;

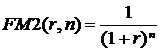— коэффициент дисконтирования, или процентный фактор настоящей стоимости (также табулируется).

Дисконтировать в соответствии с (3) можно не только единичный платеж, но и последовательность (серию) платежей (ренту, или аннуитет). Так, если F₁, F₂, ..., F_n — платежи 1-, 2-, ..., n-го периодов инвестирования, то сегодняшняя стоимость всех этих платежей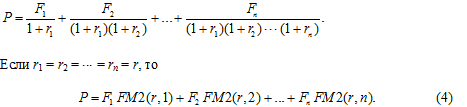

Если в состав процентной ставки не включена инфляционная составляющая, то ее необходимо учесть отдельно. (Такое может быть в случае гиперинфляции в стране, когда годовой темп инфляции превышает десятки, сотни процентов.)

Пусть темп инфляции в течение соответствующего инвестиционного периода равен t₁, t₂, ..., t_n (в долях единицы). Тогда выражение (4) должно быть записано в следующем виде: Из анализа выражения (5) следует:

1) инфляция учитывается по формуле сложных процентов;

2) современная стоимость будущих доходов с учетом инфляции составит еще меньшую величину.

Целесообразно рассмотреть два важных для практики частных случая, когда F₁ = F₂ = ... = F_n = A (постоянная рента, или постоянный аннуитет). Выражение (4) с учетом этого условия может быть приведено к виду где FM3(r, n) — процентный фактор современной стоимости аннуитета (табулируется).

Последовательность платежей можно приводить не только к текущей дате (дисконтировать), но и к любой дате в будущем. Для случая постоянного аннуитета сумма платежей, приведенная к последнему периоду инвестирования, может быть вычислена по формуле

где FM4(r, n) — процентный фактор будущей стоимости аннуитета (табулируется).

2. Оценка курсовой стоимости облигаций.

Произведем оценку курсовой стоимости облигации с постоянными купонами (Р_об). Параметры облигации следующие:

N — номинальная стоимость облигации;

K — размер годового купона (сумма процентных выплат за год);

n — число лет до погашения облигации;

r — дисконт (в качестве дисконта обычно выбирают годовую доходность по альтернативному вложению денежных средств.

Для рассматриваемого случая целесообразно взять годовой процент по депозитам в банке).

Курсовую стоимость облигации рассчитываем путем дисконтирования всех годовых доходов и номинальной стоимости (которая будет выплачена при погашении облигации) на текущую дату. Используя (3) и (6), получаем

3. Оценка курсовой стоимости акций

Оценим курсовую стоимость акций (Р_а) при следующих допущениях:

1) в каждый период (ежегодно) выплачиваются дивиденды;

2) размер дивидендов одинаков и равен D;

3) акция бессрочна;

4) дисконт от периода к периоду не меняется.

Эти допущения чрезвычайно жесткие для обыкновенных акций современных российских эмитентов и менее жесткие для привилегированных акций.

На основании выражения (4) При n, стремящемся к бесконечности, выражение (9) будет приближаться к виду

Технический анализ рынка ценных бумаг

Основополагающим принципом технического анализа является следующий: все политические, экономические, психологические и прочие факторы, которые могут воздействовать на цену товара, уже отражены в его цене (в котировках ценных бумаг). Поэтому изучать следует только тенденции изменения цен без оглядки на внешние воздействия. Так как цены изменяются под воздействием спроса и предложения, предметом исследования является также и объем торгов.

Основной целью технического анализа является установление тенденций движения цен (трендов) и обнаружение признаков изменения этих тенденций (обнаружение поворотных моментов).

Технический аналитик считает, что тенденция движения цен продолжается до тех пор, пока не появятся сигналы об ее изменении. Обнаружить эти сигналы — вот основная задача.

Для решения этой задачи строят графики (чарты) изменения цен активов за какой-либо период (рис. 2). В результате исследования этих графиков выявляют тренды и поворотные моменты.

Существует большое число методов анализа чартов. Все их можно разделить на четыре основные группы:

1) выявление и анализ фигур на графиках изменения цен;

2) следование за трендом;

3) анализ характера рынка;

4) применение структурных теорий.

Первая группа методов основана на выявлении характерных фигур на графиках изменения цен. По этим фигурам устанавливаются тенденции изменения цен (тренды) и определяются поворотные моменты. Так, в частности, считается, что повторяющиеся фигуры на графике свидетельствуют о близком значительном изменении цен.

Вторая группа методов основана на том, что тенденция, раз установившись, скорее всего сохранится, нежели изменится. Таким образом, задача сводится к тому, чтобы установить наличие тенденции и следовать ей.

Анализ характера рынка предполагает изучение не только движения цен, но и другой информации (например, объема торговли). При этом считается, что “объем следует за тенденцией”. Объем торговли на рынке “быков” возрастает в период значительного повышения курсов после их снижения и сокращается в период реакции. На рынке “медведей” объем торговли растет в период реакции и падает во время повышения цен. Считается также, что большой объем торговли сразу после резкого изменения цен означает прекращение действия текущей тенденции.

Структурный аналитик не занимается ежедневным построением графиков и изучением “фигур”. Он уверен в том, что только изучение истории фондового рынка может дать ключ к пониманию повторяющихся ситуаций. Поэтому основным предметом исследования являются сезонные изменения котировок, другие временные циклы.

Бесспорным достоинством технического анализа является его простота. Технический аналитик пользуется ограниченной информацией, касающейся, как правило, только фондовых цен и объема торговли. Такую информацию легко получить, обработать, а затем использовать в практической деятельности. При этом необходимо помнить, что технический анализ чаще всего применяется для краткосрочных прогнозов.