Многокритериальная оптимизация в задачах управления инвестиционной политикой

Введение

Основой развития сложной социально-экономической или производственной системы является разработка эффективной инвестиционной политики, при реализации которой особенно велики риски неудач и просчеты [1]. Управление инвестиционной политикой сложных систем – это всегда многокритериальная задача [2]. Инвестиционная политика нуждается в получении экономического обоснования, которое можно выработать на основе оптимизационных моделей. Существующее разнообразие подходов и моделей формирования инвестиционной политики определяется многообразием реальных ситуаций, в которых возникает такая проблема. Проблемную ситуацию следует рассматривать как «разрыв» в деятельности, «рассогласование» между целями и возможностями субъекта, необходимо понимание проблемной ситуации. Требуется адаптация общего знания к конкретному объекту. Актуальность работы определяется необходимостью постоянного совершенствования инструментария формирования эффективной инвестиционной политики в условиях неопределенности.

Теоретической базой предложенной оптимизационной модели послужили последние публикации, в которых рассматривались различные аспекты управления инвестиционной политикой в сложных социально-экономических и производственных системах.

Различные методические подходы к принятию управленческих решений в области формирования инвестиционной политики рассматриваются в работах [3-5]. Этапы и факторы, учитываемые при разработке инвестиционной политики представлены в работе [6]. В работе [7] инвестиционная политика рассматривается как механизм совершенствования экономической структуры. При разработке инвестиционной политики чаще всего используются интегральные мультипликативные критерии. Принципы разработки моделей в условиях многокритериальности рассматриваются в работах [8-10]. В состав интегрального критерия локальные критерии обычно входят с весовыми коэффициентами, учитывающими уровень важности каждого из этих критериев. Различные подходы к определению весовых коэффициентов излагаются в работах [11-13]. Одним из наиболее распространенных подходов к оценке параметров моделей формирования инвестиционной политики являются методы, разработанные на основе метода парных сравнений [14-16].

Отличительной особенностью предложенного в статье подхода является то, что кроме абстрактной математической модели многокритериальной оптимизации управления инвестиционной политикой предложен алгоритм реализации модели в условиях реальной ситуации. Основные элементы алгоритма иллюстрируются числовым примером, в основе которого лежат исследования реальной социально-экономической системы региона.

Оптимизация математической модели управления инвестиционной политикой

Пусть необходимо распределить ограниченный объем инвестиций на развитие сложной социально-экономической системы. Состояние системы описывается с помощью n групп качественных показателей эффективности функционирования системы . Обозначим оценки весовых коэффициентов значимости качественных показателей эффективности. Распределение средств определяется количеством средств, направляемых на улучшение состояния системы, характеризуемого качественными показателями эффективности. План распределения средств по направлениям задается вектором . На практике объема инвестиций недостаточно для достижения идеального состояния. Поэтому целью модели является максимальное приближение к «идеальному состоянию системы», когда качественные показатели эффективности функционирования системы выполняются на 100%. Текущее состояние системы описывается вектором оценок текущего состояния заданного в процентах. То есть, для достижения идеального состояния системы необходимо выполнение действий, улучшающих показатели эффективности на %:

(1)

Оценка средств, необходимых для достижения идеального состояния, задается вектором Тогда расход средств, необходимых на улучшения i-го показателя на 1%, определяется по формуле (2):

(2)

Следовательно единица измерения для – руб./%.

Общее улучшение i-го показателя за счет освоения выделенных средств в процентах определяется по формуле (3):

(3)

С учетом введенных обозначений математическую модель управления инвестиционной политикой можно записать в виде модели линейного программирования (4):

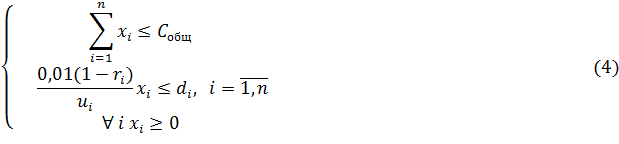
Целевая функция задачи имеет смысл среднего взвешенного значения процента достижения показателей эффективности системы идеального состояния.

Рассмотренная математическая модель является базовым вариантом модели, которая может быть усовершенствована с учетом возможностей и потребностей разработчиков инвестиционной политики системы. Например, в работе Мартышенко Н.С. рассмотрена оптимизационная модель, в которой за показателями эффективности функционирования туристского комплекса региона закреплены варианты объектов, которые направлены на повышение эффективности системы [17]. Кроме того, учитывается синергетический эффект, достигаемый за счет реализации отдельных проектов, а общий объем инвестиций необходимо распределить по периодам планирования. Методы оценки синергетического эффекта в социально-экономических системах рассматриваются также в работах [18,19].

При практической реализации оптимизационной модели важнейшим этапом является система сбора исходных данных и оцениваемых параметров, учитываемых в модели. Этапы оценки параметров оптимизационной модели представлены на рисунке 1.

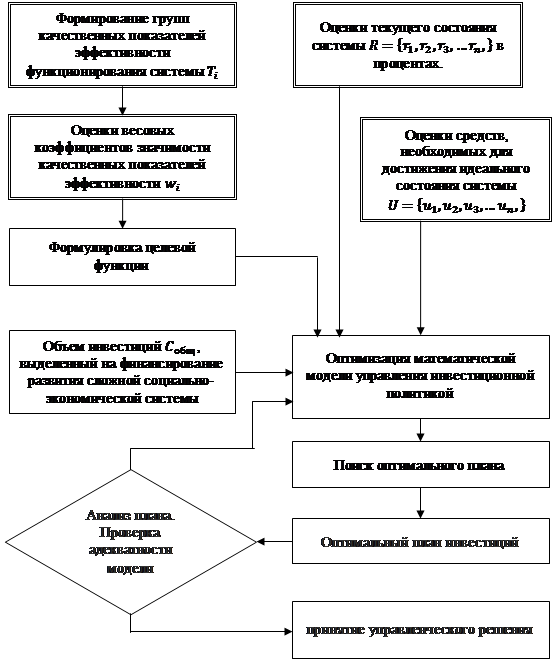
Рисунок 1. Этапы (алгоритм) оценки параметров оптимизационной модели

Источник: составлено авторами

Алгоритм включает четыре этапа оценки параметров модели (на схеме выделены двойной линией). Для оценки параметров чаще всего используется экспертная информация, получаемая методами коллективной многовариантной экспертизы [20]. Выбор методики сбора экспертной информации зависит от конкретной ситуации.

После получения оптимального решения модели оно проверяется на адекватность. Решение не должно противоречить логике сформулированной цели моделирования [21].

Противоречия могут возникать из-за неполноты учета существующих в реальности ограничений. Если модель не отвечает требованию адекватности, то целесообразно рассмотреть возможность добавления в модель новых ограничений.

Иллюстративный числовой пример оценки параметров оптимизационной модели

В качестве иллюстративного примера рассмотрим социально-экономическую систему обеспечения качества жизни региона. Вся экспертная информация касается конкретного региона – Приморского края. Рассмотрим по этапам процедуры оценки параметров оптимизационной модели.

Система наиболее существенных для населения показателей качества жизни активно исследовалась во Владивостокском государственном университете при исследовании миграционных процессов. Исследования основывались на данных мониторинга мнений населения с помощью ряда анкетных опросов, проводимых в период с 2013 по 2017 гг. За этот период в опросах приняли участие 1600 респондентов. В последние годы так же проводятся подобные исследования, но в меньших масштабах.

В процессе исследования был выделен список наиболее существенных проблем, волнующих население края. В частности, был сформирован такой список на основе систематизации ответов на открытый вопрос анкеты: «Укажите социально-экономические и другие проблемы, которые вас наиболее всего беспокоят». Для обработки данных опроса было использовано специальное программное обеспечение, позволяющее выделить типологии ответов. Всего было выделено 16 наиболее существенных проблем. Результаты обработки данных представлены в таблице 1.

Таблица 1. Параметры оптимизационной модели

В качестве весов можно выбрать частоту типологии. При большом списке проблем можно использовать и матрицу парных сравнений. В одном из опросов населения респондентам было предложено оценить степень решения в настоящее время каждой из проблем ( %). Это субъективные оценки, отражающие восприятие населением определенной проблемы.

Приближение к желаемому (идеальному) уровню удовлетворенности степенью решения проблемы в регионе призвано улучшить социальное самочувствие населения региона. Идеальное состояние должно отвечать существующим запросам населения. Со временем такие запросы могут изменяться. Например, в 60-е годы получение отдельной малогабаритной квартиры в панельном доме могло осчастливить человека. Сейчас запросы населения гораздо выше.

Для оценки средств, необходимых для достижения идеального состояния социально-экономической системы необходимо привлечение экспертов различных направлений обеспечения социально-экономических условий жизни населения в регионе.

Заключение

Рассматривается подход к многокритериальной оптимизации в задачах управления инвестиционной политикой в социально-экономических системах. Раскрываются возможности использования методов математического моделирования и оптимизации в сфере управления инвестиционной политикой. Управление эффективной инвестиционной политикой системы должно быть адекватно изменяющимся внешним условиям. При разработке оптимизационных моделей используется сочетание методов многокритериального анализа и методов коллективной многовариантной экспертизы. Предложенная модель может быть использована как инструмент формирования сбалансированной структурной политики социально-экономических систем. Модель может быть использована и в случае, когда необходимо оптимизировать выбор проектов из инвестиционного портфеля по развитию отдельного отраслевого комплекса региона.