Метод многокритериального ранжирования экономических систем

Лапаев Д.Н.¹
¹ Нижегородский государственный технический университет им. Р.Е. Алексеева

Статья в журнале

Экономическая безопасность ^{(РИНЦ, ВАК)}
опубликовать статью | оформить подписку

Том 7, Номер 8 (Август 2024)

Эта статья проиндексирована РИНЦ, см. https://elibrary.ru/item.asp?id=72103220

Аннотация:
Во многих научных и практических оптимизационных задачах поиск лучшей экономической системы не является определяющим, а востребовано сквозное исследование всех сравниваемых альтернатив для их позиционирования в рамках некоторой структуры. Предлагаемый в статье метод ранжирования обеспечивает частичное или сплошное многокритериальное структурирование сопоставляемых экономических систем по мере последовательного применения принципа Парето. Изначально принцип воздействует на исходную совокупность сравниваемых альтернатив, что обеспечивает их разделение на эффективное множество (первый ранг он же протоструктура) и остаток. Затем указанный принцип применяется к остатку, что позволяет получить второй ранг и одноименный остаток, то есть приступить к формированию квазиструктуры. Далее при необходимости на остаток предстоит последовательно воздействовать принципом Парето вплоть до установления всей иерархической структуры. Метод ранжирования станет важным компонентом теории и методологии многокритериального и многопроекционного выбора и будет востребован при разработке профильных моделей, классификаций, методик и алгоритмов для исследования широкого спектра экономических систем (как объектного, так и проектного типов) на различных уровнях управления при решении актуальных задач оценки устойчивости, безопасности, инновационности и эффективности

Ключевые слова: экономическая система, многокритериальная оптимизация, метод ранжирования, принцип Парето, эффективное множество, устойчивость, безопасность, эффективность

JEL-классификация: С61

Введение. Во многих оптимизационных научно-практических задачах в областях оценки устойчивости [14, 15, 27], безопасности [3–6, 9, 10] и инновационности [2, 11, 17, 18, 26, 28] поиск единственной экономической системы [11, 17, 19] не является основным, а востребовано сквозное исследование всей совокупности сравниваемых альтернатив (вариантов) для позиционирования последних в рамках некоторой структуры [1, 7, 8, 12, 13, 14]. Комплексную оценку состояния экономических систем, как правило, обеспечивает использование нескольких блоков (проекций) показателей [16, 20–25]. Так, по блочному принципу сформирована общая математическая модель мировой динамики [29]: 1) климат, природная среда, 2) экология, 3) технологии, 4) демография, 5) экономика (производство, экономические отношения), 6) социосфера (социальные взаимодействия), 7) политика (государственное управление, политические взаимодействия). В ней каждому блоку (проекции) соответствует своя частная модель. При исследовании экономической безопасности на мезоуровне рассматривают 10 проекций: макроэкономическое развитие, промышленная безопасность, продовольственная безопасность, энергетическая безопасность, бюджетно-финансовая безопасность, кадровая безопасность, инновационное развитие, социальное развитие, экологическое развитие, внешнеэкономическое развитие [30]. Однако частные экономические задачи успешно решаются в однопроекционной (многокритериальной) постановке.

Для обозначения результатов иерархического многокритериального компаративного анализа оперируют понятием ранга, под которым понимают совокупность вариантов (альтернатив), выделенных на основании некоторого принципа (правила) [12]. В нашем случае это базовый принцип Парето, согласно которому решение есть совокупность взаимно несравнимых (неулучшаемых) экономических систем.

Его использование для анализа исходного набора альтернатив позволяет сформировать эффективное множество, которое называют также множеством первого ранга. Последовательная реализация принципа при исследовании оставшихся вариантов дает возможность получить второй и нижестоящие ранги. Для регламентации процесса ранжирования потребуется разработка профильного научного метода.

Основная часть. Предлагаемый в статье метод ранжирования обеспечивает частичное или сплошное многокритериальное структурирование сопоставляемых экономических систем по мере последовательного применения принципа Парето. Формализованная постановка имеет следующий вид. Принятие решения осуществляется некоторой заинтересованной стороной, руководствующейся собственными целями Ц = {Ц_i}, . Исследование может проводиться на конкретную дату (настоящую, прошедшую, будущую) либо в динамике. Сравнению подлежат экономические системы S = {S_i}, . При принятии решения задействуются показатели К = {К_j}, , обеспечивающие надлежащий учет всех аспектов оптимизационной задачи. Требуется определить первый и нижестоящие ранги.

Суть метода заключается в следующем (рис. 1).

Изначально принцип Парето воздействует на исходную совокупность сравниваемых альтернатив, что обеспечивает их разделение на эффективное множество М_эф (первый ранг он же протоструктура) и остаток. Затем указанный принцип применяется к остатку, что позволяет получить второй ранг М_2р и одноименный остаток, то есть приступить к формированию квазиструктуры. Приставка квази здесь означает, что исследование не завершено в полном объеме и может быть продолжено. Далее при необходимости на остаток предстоит последовательно воздействовать принципом Парето вплоть до установления всей иерархической структуры.

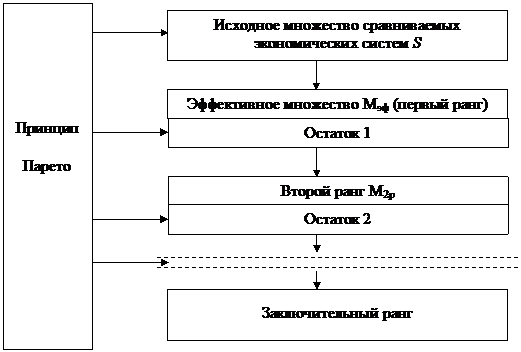
Рисунок 1. Логическая схема метода многокритериального

ранжирования экономических систем

Источник: составлено автором

Отметим, что метод ранжирования допускает корректировку параметров в виде пересмотра состава сравниваемых экономических систем, показателей, инструментария прогнозирования, планирования и импутации данных, даты проведения исследования, исходной цели, состава стейкхолдеров. Вместе с тем необходимо исключить манипуляции в интересах выхода на желаемый результат вопреки научно обоснованному решению.

Для пояснения сущности метода рассмотрим пример выделения ранговой структуры при исследовании состояния экономических систем S₁–S₁₀ по трем показателям К₁–К₃ в восьми ситуациях.

Ситуация 1

Все показатели требуется максимизировать.

Построение эффективного множества начнем с формирования сортированного массива. Для этого упорядочим по мере возрастания значений показателей номера 1–10 сравниваемых экономических систем. Здесь и далее в массивах эффективные варианты выделены жирным шрифтом. Итерация 1.

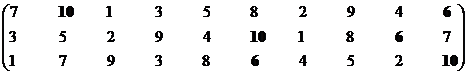
Неэффективны (слева от оптимумов)	Эффективны (крайние правые системы)
1, 3, 8, 9	6
	7
	10
Остаток 2, 4, 5

Итерация 2.

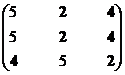
Неэффективны	Эффективны
	4
5	2
	Решение 2, 4, 6, 7, 10

По итогам двух итераций множество эффективных экономических систем запишем в виде М_эф = {S₂, S₄, S₆, S₇, S₁₀}. Дальнейшему анализу подлежат альтернативы S₁, S₃, S₅, S₈ и S₉.

Построение множества второго ранга.

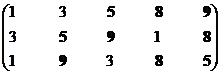
Неоптимальны (слева от оптимумов)	Оптимальны (крайние правые системы)
	9
1, 3	8
	5
	Решение 5, 8, 9

Следовательно, множество систем второго ранга примет вид М_2р = {S₅, S₈, S₉}. Оптимальные варианты выделены жирным шрифтом в массивах. Взаимно несравнимые альтернативы S₁ и S₃ составят заключительный третий ранг.

Структура включает три ранга: первый ранг (протоструктура) представлен пятью экономическими системами, второй – тремя и третий – двумя.

Ситуация 2

Необходимо минимизировать показатели К₁ и К₂ и максимизировать показатель К₃. Поменяем в первой и второй строках порядок следования номеров на обратный.

Формирование эффективного множества, итерация 1.

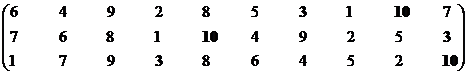
Неэффективны	Эффективны
	7
9	3
1, 6, 8	10
Остаток 2, 4, 5

Итерация 2.

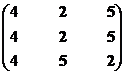
Неэффективны	Эффективны
4	5
	2
	Решение 2, 3, 5, 7, 10

Множество эффективных систем – М_эф = {S₂, S₃, S₅, S₇, S₁₀}, тогда дальнейшему анализу подлежат альтернативы S₁, S₄, S₆, S₈ и S₉.

Построение множества второго ранга.

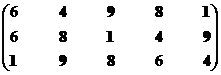
Неоптимальны	Оптимальны
	1
	9
6	4
Остаток 8	Решение 1, 4, 8, 9

Множество систем второго ранга примет вид М_2р = {S₁, S₄, S₈, S₉}. Альтернатива S₆ составит заключительный третий ранг.

Структура включает три ранга: первый ранг представлен пятью экономическими системами, второй – четырьмя, а третий – одной.

Ситуация 3

Требуется минимизировать показатель К₁ и максимизировать показатели К₂ и К₃. Сообразно этому перестраиваем массив.

Формирование эффективного множества.

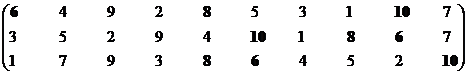
Неэффективны	Эффективны
1	7
2–5, 9	10
Остаток 6, 8 (несравнимы)	Решение 6, 7, 8, 10

Множество эффективных систем – М_эф = {S₆, S₇, S₈, S₁₀}, поэтому дальнейшему анализу подлежат альтернативы S₁–S₅ и S₉.

Построение множества второго ранга, итерация 1.

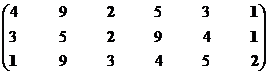
Неоптимальны	Оптимальны
	1
	2
Остаток 3–5, 9

Итерация 2.

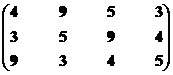
Неоптимальны	Оптимальны
	3
	4
	5
Остаток 9	Решение 1, 2, 3, 4, 5, 9

Множество второго ранга примет вид М_2р = {S₁, S₂, S₃, S₄, S₅, S₉}.

Структура включает два ранга: первый ранг представлен четырьмя экономическими системами, а второй – шестью.

Ситуация 4

Необходимо максимизировать показатели К₁ и К₃ и минимизировать показатель К₂. Корректируем массив.

Формирование эффективного множества, итерация 1.

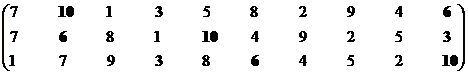
Неэффективны	Эффективны
7	6
1, 7	3
7	10
Остаток 2, 4, 5, 8, 9

Итерация 2.

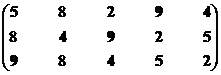
Неэффективны	Эффективны
8	4
	5
8	2
Остаток 9	Решение 2, 3, 4, 5, 6, 9, 10

Множество эффективных систем – М_эф = {S₂, S₃, S₄, S₅, S₆, S₉, S₁₀}, тогда дальнейшему анализу подлежат альтернативы S₁, S₇ и S₈.

Построение множества второго ранга.

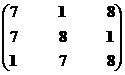
Неоптимальны	Оптимальны
7	8
	1
	Решение 1, 8

Тогда множество систем второго ранга примет вид М_2р = {S₁, S₈}. Вариант S₇ составит заключительный третий ранг.

Структура включает три ранга: первый ранг представлен семью экономическими системами, второй – двумя и третий – одной.

Ситуация 5

Требуется максимизировать показатели К₁ и К₂ и минимизировать показатель К₃. Перестраиваем массив.

Формирование эффективного множества, итерация 1.

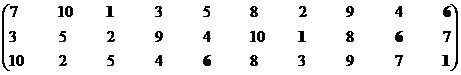
Неэффективны	Эффективны
2, 4, 5, 10	6
	7
10	1
Остаток 3, 8, 9

Итерация 2.

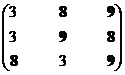
Неэффективны	Эффективны
3	9
	8
	Решение 1, 6, 7, 8, 9

Множество эффективных систем – М_эф = {S₁, S₆, S₇, S₈, S₉}, поэтому дальнейшему анализу подлежат альтернативы S₂–S₅ и S₁₀.

Построение множества второго ранга.

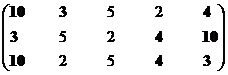
Неоптимальны	Оптимальны
2, 5	4
	10
	3
	Решение 3, 4, 10

Таким образом, множество систем второго ранга примет вид М_2р = {S₃, S₄, S₁₀}. Взаимно несравнимые варианты S₂ и S₅ составят заключительный третий ранг.

Структура включает три ранга: первый ранг представлен пятью экономическими системами, второй – тремя и третий – двумя.

Ситуация 6

Все показатели необходимо минимизировать. Корректируем массив.

Формирование эффективного множества.

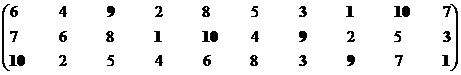
Неэффективны	Эффективны
	7
2, 4–6, 8	3
6, 8	1
Остаток 9, 10 (несравнимы)	Решение 1, 3, 7, 9, 10

Множество эффективных систем – М_эф = {S₁, S₃, S₇, S₉, S₁₀}, тогда дальнейшему анализу подлежат альтернативы S₂, S₄–S₆ и S₈.

Построение множества второго ранга.

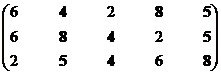
Неоптимальны	Оптимальны
2	5
6	8
Остаток 4	Решение 4, 5, 8

При этом множество систем второго ранга примет вид М_2р = {S₄, S₅, S₈}. Взаимно несравнимые варианты S₂ и S₆ составят заключительный третий ранг.

Ситуация 7

Требуется минимизировать показатели К₁ и К₃ и максимизировать показатель К₂. Перестраиваем массив.

Формирование эффективного множества.

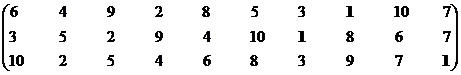
Неэффективны	Эффективны
2–6, 8–10	7
	1
	Решение 1, 7

Множество эффективных систем – М_эф = {S₁, S₇}, поэтому дальнейшему анализу подлежат альтернативы S₂–S₆ и S₈–S₁₀.

Построение множества второго ранга, итерация 1.

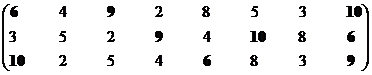
Неоптимальны	Оптимальны
	10
	6
	9
Остаток 2–5, 8

Итерация 2.

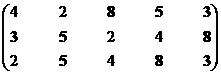
Неоптимальны	Оптимальны
	3
2, 4	8
Остаток 5	Решение 3, 5, 6, 8, 9, 10

Множество систем второго ранга примет вид М_2р = {S₃, S₅, S₆, S₈, S₉, S₁₀}. Взаимно несравнимые варианты S₂ и S₄ составят заключительный третий ранг.

Структура включает три ранга: первый и последний ранги представлены двумя экономическими системами, а второй – шестью.

Ситуация 8

Необходимо максимизировать показатель К₁ и минимизировать показатели К₂ и К₃. Корректируем массив.

Формирование эффективного множества, итерация 1.

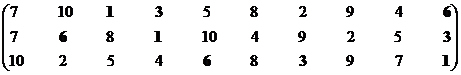
Неэффективны	Эффективны
	6
10	3
7	1
Остаток 2, 4, 5, 8, 9

Итерация 2.

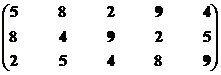
Неэффективны	Эффективны
	4
	5
8	9
Остаток 2	Решение 1, 2, 3, 4, 5, 6, 9

Множество эффективных систем – М_эф = {S₁, S₂, S₃, S₄, S₅, S₆, S₉}, тогда дальнейшему анализу подлежат альтернативы S₇, S₈ и S₁₀.

Построение множества второго ранга.

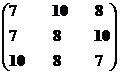
Варианты взаимно несравнимы. Таким образом, множество вариантов второго ранга примет вид М_2р = {S₇, S₈, S₁₀}.

Структура включает два ранга: первый ранг представлен семью экономическими системами, а второй – тремя. Суть метода ясна.

Заключение

Метод ранжирования станет важным компонентом теории и методологии многокритериального и многопроекционного выбора и будет востребован при разработке профильных моделей, классификаций, методик и алгоритмов для исследования широкого круга экономических систем как объектного, так и проектного типов на различных иерархических уровнях при решении актуальных задач оценки устойчивости, безопасности, инновационности и эффективности.

Источники:

1. Аленкова И.В., Лапаева О.Н. Безопасность регионов Центрального федерального округа в экономико-инновационном аспекте // Развитие и безопасность. – 2023. – № 1 (17). – c. 74–83. – doi: 10.46960/2713-2633_2023_1_74.
2. Артемьев Н.В., Лапаев Д.Н., Корнилов Д.А., Митякова Е.В. Инновационное развитие моногородов как императив их экономической безопасности. / Монография. - Нижний Новгород: НГТУ, 2023. – 116 c.
3. Банк С.В., Лапаев Д.Н., Хусаинов М.К. Методы обеспечения экономической безопасности хозяйствующего субъекта от угроз теневой экономики // Russian Journal of Management. – 2024. – № 1. – c. 380–389. – doi: 10.29039/2409-6024-2024-12-1-380-389.
4. Бухвальд Е.М., Лапаев Д.Н. Вариации стратегического планирования и риски для экономической безопасности России // Вестник Нижегородского университета им. Н.И. Лобачевского. Серия: Социальные науки. – 2022. – № 2(66). – c. 7–13. – doi: 10.52452/18115942_2022_2_7.
5. Вакуленко Р.Я., Лапаев Д.Н., Виноградова О.В., Соколов Р.Н. Технологии преодоления экономических санкций. Иранский опыт // Научные исследования и разработки. Экономика фирмы. – 2022. – № 3. – c. 82–90. – doi: 10.12737/2306-627X-2022-11-3-82-90.
6. Кузнецова С.Н., Лапаев Д.Н. Обеспечение комплексной экономической безопасности техно- и промышленных парков // Экономическая безопасность. – 2024. – № 4. – c. 951-966. – doi: 10.18334/ecsec.7.4.120939.
7. Лапаев Д.Н., Лапаева О.Н., Поташник Я.С. Безопасность обрабатывающих производств Владимирской области в экономико-инновационном аспекте // Экономика, предпринимательство и право. – 2023. – № 8. – c. 3005-3018. – doi: 10.18334/epp.13.8.118743.
8. Лапаев Д.Н. Безопасность регионов Приволжского федерального округа в экономико-инновационном аспекте // Экономическая безопасность. – 2023. – № 1. – c. 291-314. – doi: 10.18334/ecsec.6.1.117300.
9. Лапаев Д.Н., Митяков Е.С. Методика многокритериальной оценки экономической безопасности регионов России (на примере Приволжского федерального округа) // Экономика, статистика и информатика. Вестник УМО. – 2013. – № 4. – c. 151–154.
10. Лапаев Д.Н. Методические подходы к анализу и оценке угроз экономической безопасности в социальной сфере // Интернет-журнал Науковедение. – 2016. – № 5(36). – c. 41.
11. Лапаев Д.Н., Лапаева О.Н. Многокритериальная методика выбора предпочтительных вариантов при сравнении инновационной деятельности отраслей промышленности // Аудит и финансовый анализ. – 2014. – № 5. – c. 113–116.
12. Лапаев Д.Н. Многокритериальное принятие решений в экономике. / Монография, 2-е изд. - Нижний Новгород: НГТУ, 2016. – 281 c.
13. Лапаев Д.Н. Многопроекционная оценка безопасности регионов Приволжского федерального округа в экономико-инновационном аспекте // Экономическая безопасность. – 2024. – № 2. – c. 425-442. – doi: 10.18334/ecsec.7.2.120476.
14. Лапаев Д.Н., Лапаева О.Н., Поташник Я.С. Многопроекционная оценка устойчивости регионов Сибирского федерального округа // Развитие и безопасность. – 2024. – № 2 (22). – c. 90–99.
15. Лапаев Д.Н., Митяков Е.С., Мокрецова Е.С. Мониторинг устойчивого развития отраслей промышленности на основе многокритериального подхода // Экономика, статистика и информатика. Вестник УМО. – 2013. – № 5. – c. 168–171. – doi: RPFQBP.
16. Лапаев Д.Н., Лапаева О.Н. Принципы выбора многопроекционного решения в экономике // Аудит и финансовый анализ. – 2015. – № 4. – c. 415–417.
17. Лапаев Д.Н., Лапаева О.Н. Формирование методики определения предпочтительных вариантов при сравнении инновационной деятельности отраслей промышленности по совокупности показателей // Аудит и финансовый анализ. – 2014. – № 3. – c. 373–375.
18. Лапаева О.Н., Митякова Е.В. Концептуальная модель обеспечения инновационной деятельности монопрофильных территорий // Развитие и безопасность. – 2022. – № 4 (16). – c. 31–42. – doi: 10.46960/2713-2633_2022_4_31.
19. Лапаева О.Н. Многокритериальная оценка экономического состояния предприятий и отраслей промышленности и выбор предпочтительных альтернатив. / Монография. - Нижний Новгород: НГТУ, 2015. – 145 c.
20. Лапаева О.Н. Многопроекционная оценка состояния промышленных экономических систем. / Монография. - Нижний Новгород: НГТУ, 2018. – 371 c.
21. Лапаева О.Н. Многопроекционная сравнительная оценка альтернатив в экономике. / Монография. - Нижний Новгород: НГТУ, 2017. – 210 c.
22. Лапаева О.Н. Постановка и анализ задач многопроекционного принятия решений в экономике // Гуманизация образования. – 2015. – № 3. – c. 112–116.
23. Лапаева О.Н. Проекционный подход к сравнительной оценке альтернатив в экономике // Современная наука: актуальные проблемы и пути их решения. – 2017. – № 1(32). – c. 41–43.
24. Лапаева О.Н. Принцип ранжированного выбора взаимоприемлемого многопроекционного прогнозного решения // Конкурентоспособность в глобальном мире: экономика, наука, технологии. – 2017. – № 1-1(26). – c. 105–108.
25. Лапаева О.Н. Принцип эффективного выбора взаимоприемлемого многопроекционного прогнозного решения // Конкурентоспособность в глобальном мире: экономика, наука, технологии. – 2017. – № 1-1 (26). – c. 102–104.
26. Митяков С.Н., Лапаев Д.Н., Митяков Е.С., Ладынин А.И. Мониторинг научно-технологической безопасности регионов России: многокритериальный анализ // Инновации. – 2022. – № 3 (281). – c. 18–25. – doi: 10.26310/2071-3010.2022.281.3.003.
27. Митяков С.Н., Лапаев Д.Н., Катаева Л.Ю., Рамазанов С.А. Устойчивое развитие и угрозы экономической безопасности // Экономика и предпринимательство. – 2019. – № 10 (111). – c. 111–114.
28. Морозова Г.А., Мальцев В.А., Мальцев К.В., Лапаев Д.Н. Инновационное развитие промышленных комплексов в регионе. / Монография. - Нижний Новгород: ВВАГС, 2010. – 160 c.
29. Садовничий В.А. Преодолевая пределы роста. Основные положения доклада для Римского клуба. / Монография. - М.: МГУ, 2023. – 99 c.
30. Митяков С. Н. Экономическая безопасность регионов России. / Монография, 3-е изд. - Нижний Новгород: Нижегород. гос. техн. ун-т им. Р.Е. Алексеева, 2019. – 299 c.

Страница обновлена: 30.11.2024 в 10:46:25

Подробнее об авторе: