Концептуальный подход к оценке продовольственной безопасности макрорегиона на основе использования методов математического моделирования

Введение

Актуальность разработки теоретических и методических основ оценки продовольственной безопасности обусловлена потребностями модернизации системы продовольственного обеспечения территорий Российской Федерации в условиях нарастания внешних и внутренних угроз, а также практической значимостью своевременного прогнозирования продовольственного дефицита и предотвращения кризисных явлений с учетом новых глобальных и национальных трендов в агропромышленном комплексе (АПК).

Важность оценки продовольственной безопасности на макрорегиональном уровне предопределена необходимостью регионов Российской Федерации кооперационной деятельности с целью достижения рекомендуемых показателей в сфере продовольствия в рамках существующего спроса на продукцию АПК, изменений потребительских предпочтений, распространения умного сельского хозяйства, изменений климата и роста нагрузки на ресурсы [1] (Ruiga, Kovzunova, Stupina, Kashina, Burmenko, 2020).

Анализ действующей нормативно-правовой базы в области обеспечения продовольственной безопасности показывает, что текущее федеральное и региональное законодательство представляет набор законов и подзаконных актов, слабо связанных между собой, в связи с чем закрепленная методика оценки продовольственной безопасности, утвержденная Указом Президента РФ от 21 января 2020 г. № 20 в Доктрине продовольственной безопасности Российской Федерации, не учитывает территориальные особенности страны, а отсутствие закрепленной системы целевых индикаторов и их пороговых значений не позволяет осуществлять корректную оценку продовольственной безопасности на макрорегиональном уровне.

Существующая рассогласованность показателей и критериев оценки продовольственной безопасности является причиной отсутствия взаимосвязи в оценочных параметрах и логики интерпретации полученных значений, что, в свою очередь, приводит к несвоевременной идентификации угроз продовольственной безопасности и нарушению продовольственной устойчивости регионов и макрорегионов.

Учитывая обозначенную проблематику исследовательских вопросов, обусловленную недостаточно полной проработкой методических аспектов по вопросам оценки продовольственной безопасности на региональном и макрорегиональном уровне, целью данного исследования является формирование концептуального подхода к оценке продовольственной безопасности макрорегиона с включением методов математического моделирования, позволяющих осуществлять проверку результатов проведенной оценки с последующей идентификацией наиболее значимых параметров, требующих особого внимания при принятии управленческих решений.

Для целей данного исследования целесообразно конкретизировать содержание понятия «продовольственная безопасность макрорегиона». По мнению авторов, продовольственная безопасность макрорегиона может быть определена как состояние экономики ограниченного территориального объединения с ярко выраженной хозяйственной специализацией, при котором население обеспечивается качественным и доступным продовольствием, нормальным уровнем жизни, исключающим возможность появления острого недоедания, достигаемое путем стимулирования развития продовольственных инноваций за счет межрегионального взаимодействия, направленных на обеспечение отечественного производства продукции, за счет рационального использования ресурсного потенциала.

Материалы и методы

В настоящее время на законодательном уровне для оценки продовольственной безопасности закреплена только одна методика, в основу которой заложена система общепризнанных показателей, индикаторов и критериев, определяемых Правительством Российской Федерации. Данная методика представлена в Доктрине продовольственной безопасности и включает четыре основных критерия: производственная независимость, экономическая доступность, физическая доступность, соответствие пищевой продукции требованиям законодательства Евразийского экономического союза о техническом регулировании [2]. Методика ориентирована, прежде всего, на оценку продовольственной безопасности на федеральном уровне. Применение методики на макрорегиональном уровне является сомнительным, что связано в первую очередь с расчетом показателя продовольственной независимости, система пороговых значений которого в конечном итоге не учитывает специфические особенности территорий, включая неблагоприятные природно-климатические, географические и другие факторы, которые создают препятствия для производства всех перечисленных в Доктрине видов сельскохозяйственной продукции, сырья и продовольствия. Кроме того, в методике упущена процедура валидации норм потребления продовольственных товаров, которая необходима для адекватной и соизмеримой оценки продовольственной безопасности на макрорегиональном уровне.

Исследование альтернативных теоретических подходов к оценке продовольственной безопасности позволяет сделать вывод о том, что в большинстве случаев методики оценивания также сводятся к изучению трех основных показателей, таких как производственная независимость, экономическая и физическая доступность продовольствия. При этом исключается возможность адаптации к макрорегиональному уровню, несмотря на всю важность и актуальность данной рассматриваемой категории.

Так, в зарубежных исследовательских направлениях по вопросам оценки продовольственной безопасности, представленных в работах Чарльза Николсона, Эммы Стивенс [3] (Nicholson, Stephens, Kopainsky, Jones, Parsons, Garrett, 2021), авторы используют индексный подход к оцениванию, рассматривая такие показатели, как наличие, доступность и потребление продовольствия, не включая при этом в систему оценки социальный блок, отражающий уровень жизни населения. Аналогичный подход представлен в работах Ларисы Михореану, Марианы Лауры Кисмаш [4] (Mihoreanu, Cismaş, Dănilă (Jianu), 2019) и По-Чи Чен, Мин-Миин Ю [5] (Chen, Yub, Shihc, Chang, Hsu, 2019). Исследование авторов основывается на изучении глобального индекса продовольственной безопасности (GFSI), включающего три блока оценки: 1) доступность; 2) наличие; 3) безопасность и качество. Недостатком подходов является субъективизм и невозможность корректной идентификации удельного веса показателей. Общее отличие трех авторских подходов заключается в частных показателях, используемых в блоках методики GFSI.

Расширили систему оценки продовольственной безопасности Семен ван Беркум и Руэрд Рубен [6] (Berkum, Ruben, 2021), используя индексный метод и метод невзвешенной агрегации. Авторы рассматривают два блока показателей (компоненты продовольственной системы и результаты деятельности продовольственной системы), однако не затрагивают социальный аспект. Комплексную систему оценивания на основе составного индекса измерения многомерной концепции продовольственной безопасности (индекс Протея), включающую показатели обеспеченности продовольствием, экономической и физической доступности, а также оценку стабильности, как экономической, так и социально-политической, предложили Оскар Мария Каккавале и Валерио Джифридо [7] (Caccavale, Giuffrida, 2020). Авторы применили математические методы для устранения источников неопределенности, присущих построению составного показателя, а также расширили зону оценки, рассмотрев социальный аспект, а также блок факторов влияния опасных природных явлений окружающей среды.

Недостатком рассмотренных зарубежных подходов является сложность в нормализации, взвешивании и агрегировании переменных, а также в установлении пороговых значений, предложенные показатели не являются закрепленными на законодательном уровне и, как глобальный индекс продовольственной безопасности (GFSI), могут быть адаптированы только для федерального уровня.

Отечественные авторы также рассматривают вопрос оценки продовольственной безопасности, наиболее распространенными методами являются экспертный, метод интегральной оценки и индексный метод. Так, придерживаются первого направления такие авторы, как Антамошкина Е.Н. [8] (Antamoshkina, 2014), Оловянников Д.Г. [9] (Olovyannikov, 2009), Омелай А.Ю. [10] (Omelay, 2014). В своих методиках по каждому показателю авторы предлагают критерии, позволяющие в баллах оценить уровень продовольственной безопасности как оптимальный, допустимый или низкий. Основной проблемой подходов является субъективизм балльной оценки и установленных диапазонов, а также отсутствие в системах оценки ориентации на особенности продовольственного производства и существующих производственных мощностей.

Метод интегральной оценки рассмотрен в работах Терентьева Ю.И [11] (Terentev, 2004), в соответствии с данной методикой коэффициент продовольственной безопасности определяется как сумма коэффициентов элементов продовольственной независимости. Для исключения отрицательных значений показателя в аддитивную модель вводят свободный коэффициент. Недостатком подхода является ограниченность в перечне учитываемых коэффициентов, не затрагиваются в оценке такие аспекты, как качество и безопасность продовольствия, темп роста цен на продукты питания, состояние АПК в регионе.

В наибольшей степени отечественные авторы придерживаются индексного метода оценки, данный подход представлен в работах Хромова Ю.С., Костяева А.И., Тимофеева М.У. [12] (Kostousenko, 2009), Смирнова В.В. [13] (Smirnov, 2015), Маслакова В.В. [14] (Maslakov, 1998), Лысоченко А.А. [15] (Lysochenko, 2009), Алтухова А.И. [16] (Alutkhov, 2016), Потапова А.П. [17] (Potapov, 2019), Анфиногентовой А.А., Крылатых Э.Н. [18] (Anfinogentova, 2013), Яшковой Н.В. [19] (Yashkova, 2019). В основе каждого подхода рассматривается система индикаторов, в результате оценки которой формируется вывод о состоянии продовольственной безопасности. Основными недостатками индексного метода оценки являются отсутствие математически обоснованных пороговых значений, наличие качественных показателей, а также невозможность сведения показателей к интегральному индексу.

Учитывая вышеизложенное, представляется возможным осуществить группировку авторских подходов к оценке продовольственной безопасности по двум параметрам с целью идентификации важных и возможных к адаптации критериев для оценки продовольственной безопасности на уровне макрорегиона:

1) укрупненная группа критериев, включенная в систему оценки состояния продовольственной безопасности регионов;

2) укрупненная группа методов, включенная в систему оценки состояния продовольственной безопасности регионов.

Таким образом, в наибольшей степени отечественные и зарубежные авторы включают в оценку продовольственной безопасности такие критерии, как территориальная специализация самообеспеченности территории (продовольственная независимость), физическая и экономическая доступность, используя разные наборы показателей для оценки данных параметров. Особое внимание авторы уделяют оценке продовольственного потенциала территорий, а также пищевой ценности и безопасности продовольствия. Это позволяет учитывать территориальные особенности при оценке продовольственной безопасности и включать процедуру валидации норм продовольственного потребления. В условиях проблемы измерения показателей в наименьшей степени в авторских подходах представлены критерии достаточности продовольствия, количественной доступности, ввозимости продовольствия и качества продукции (рис. 1).

Рисунок 1. Группировка авторских подходов по критериям, включенным в систему оценки продовольственной безопасности

Источник: составлено авторами.

Анализируя рассмотренные подходы по второму критерию «укрупненная группа методов, включенная в систему оценки состояния продовольственной безопасности регионов», можно сделать вывод, что чаще всего авторы используют такие методы, как метод экспертных оценок (Антамошкина Е.Н.), индексный метод (Хромов Ю.С., Костяев А.И., Тимофеев М.У., Смирнов В.В., Маслаков В.В., Лысоченко А.А, Алтухов А.И., Larisa Mihoreanu, Oscar Maria Caccavale, Siemen van Berkum, Po-Chi Chena, Charles F. Nicholson), а также комбинацию методов экспертных оценок и индикативного подхода с последующим расчетом интегрального показателя (Оловянников Д.Г., Терентьев Ю.И., Омелай Ю.А.).

Результаты

В результате проведенного исследования представляется целесообразным разработать комплексную методику оценки продовольственной безопасности макрорегиона, учитывающую достоинства изученных научных подходов и исключающую выявленные в ходе исследования недостатки. Данная методика позволит получить релевантные результаты на основе принципов системности, комплексности, научности, постоянства исследований и взаимосвязи данных с последующим включением методов математического моделирования для проверки полученных значений.

Предлагается использовать следующий алгоритм оценки, включающий последовательное выполнение определенных этапов (рис. 2).

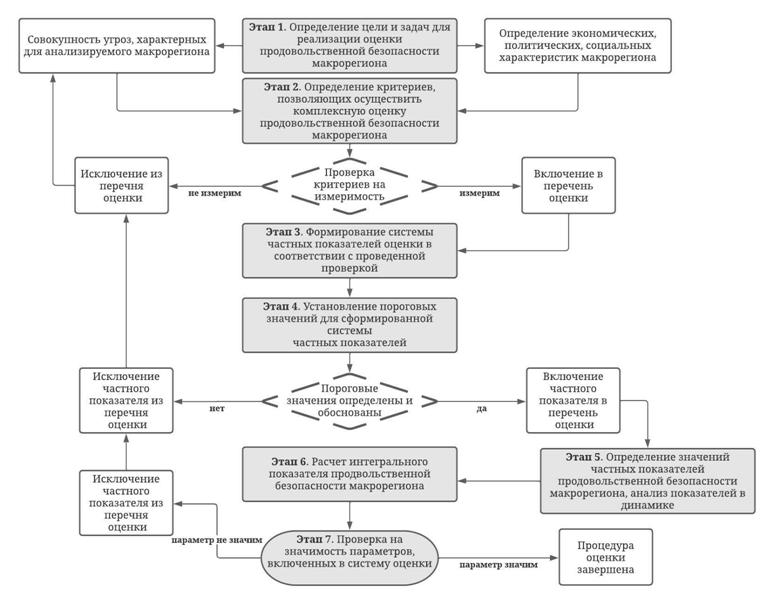
Рисунок 2. Алгоритм оценки продовольственной безопасности макрорегиона

Источник: составлено авторами.

На первоначальном этапе реализации алгоритма оценки предполагается сбор, систематизация и последующий анализ информации об экономических, политических и социальных особенностях оцениваемого макрорегиона с последующей первичной идентификацией угроз, характерных для объекта исследования. Полученная информация является базой для формирования и определения цели и задач оценки продовольственной безопасности макрорегиона.

Второй этап алгоритма базируется на определении критериев, позволяющих осуществить комплексную оценку продовольственной безопасности макрорегиона. В качестве критериев оценки предполагается принимать объективные параметры, имеющие очевидное влияние на объект исследования, отражающие явные его особенности, при воздействии на которые объект исследования претерпевает динамические изменения. Каждый подобранный критерий проходит процедуру проверки на измеримость с целью исключения субъективного фактора. Критерий считается «измеримым», если существует объективная возможность подбора необходимых показателей, позволяющих оценить, измерить состояние или положение рассматриваемого критерия в рамках анализируемого объекта исследования.

С авторской точки зрения, базируясь на результатах проведенного анализа, целесообразно включить в систему оценки продовольственной безопасности макрорегиона следующую совокупность критериев:

1) физическая доступность продовольствия (критерий позволяет оценить бесперебойность поступления продовольствия в места потребления в объемах и ассортименте, соответствующих платежеспособному спросу);

2) экономическая доступность продовольствия (критерий позволяет оценить распределение продовольственных товаров между различными социальными группами населения при сложившемся уровне цен и доходов);

3) достаточность потребления продовольствия (критерий позволяет оценить потребление населением определенного набора продуктов питания, минимально необходимого по установленным медицинским нормам);

4) безопасность продовольствия (критерий позволяет оценить соответствие ввозимой и местной продукции стандартам качества на основе данных выборочных инспекционных проверок, проводимых Управлением Госинспекции по торговле, качеству, защите прав потребителей);

5) транспортная доступность (критерий позволяет оценить возможность и расположенность территорий к круглогодичным и бесперебойным поставкам продовольствия и других жизненно необходимых товаров для населения);

6) устойчивость продовольственной системы (критерий позволяет оценить возможность продовольственной системы в экстренных случаях продолжать поддерживать необходимые объемы питания населения).

Третий и четвертый этапы алгоритма основываются на «измеримости» подобранных критериев оценки продовольственной безопасности макрорегиона. В зависимости от цели исследования формируется совокупность частных показателей, позволяющая оценить состояние продовольственной безопасности. Далее для частных показателей устанавливаются пороговые значения на основании существующих нормативно-правовых регламентов, результатов ранее проведенных исследований или закономерностей, выявленных в ходе изучения специфики макрорегиона (первый этап алгоритма). Авторами предложена следующая система критериев и частных показателей оценки уровня продовольственной безопасности макрорегиона, представленная в соответствии с таблицей 1.

Таблица 1

Система критериев и частных показателей оценки уровня продовольственной безопасности макрорегиона

Источник: составлено авторами.

Пятый этап алгоритма предусматривает расчет частных показателей оценки продовольственной безопасности макрорегиона и завершается процедурой простого нормирования значений. При этом нормировка значений рассчитывается как отношение фактического значения к пороговому, если желательно увеличение соответствующего показателя продовольственной безопасности, и наоборот, если желательно его снижение.

Предполагается, что наивысшая степень продовольственной безопасности будет достигнута при условии, что весь комплекс частных показателей будет находиться в пределах допустимых границ своих пороговых значений, а пороговые значения одного частного показателя будут достигаться не в ущерб другим.

Также стоит отметить, что введенные пороговые значения частных показателей являются предельными величинами и характеризуют нормальный ход развития различных элементов в области продовольственной безопасности. Если показатели приближаются к их предельно допустимой величине, то это свидетельствует о нарастании угроз социально-экономической стабильности общества, если превышают пороговые значения – о вступлении общества в зону нестабильности и социальных конфликтов, то есть о реальном подрыве продовольственной безопасности.

Шестым этапом алгоритма является расчет интегрального показателя продовольственной безопасности, который определяется путем расчета суммы оценок критериев продовольственной безопасности в соответствии с формулой (1):

ИППБ=0,2*Ф+0,2*Э+0,15*Д+0,15*Б+0,15*Т+0,15*У, (1)

где Ф – физическая доступность; Э – экономическая доступность; Д – достаточность потребления продовольствия; К – безопасность продовольствия; Т – транспортная доступность; У – устойчивость продовольственной системы.

Полученные значения интегрального показателя предлагается интерпретировать следующим образом:

– ИППБ < 0,5 – критический уровень продовольственной безопасности макрорегиона;

– 0,5 ≤ ИППБ < 0,7 – кризисный уровень продовольственной безопасности макрорегиона;

– 0,7 ≤ ИППБ < 0,9 – низкий уровень продовольственной безопасности макрорегиона;

– 0,9 ≤ ИППБ < 1 – нормальный уровень продовольственной безопасности макрорегиона;

– ИППБ ≥ 1 – высокий уровень продовольственной безопасности макрорегиона.

Завершающим этапом алгоритма является процедура проверки включенных частных показателей на значимость в формировании интегрального показателя. Процедура проверки базируется на использовании методов математического моделирования. С авторской точки зрения, в рамках оценки продовольственной безопасности могут быть использованы метод Монте-Карло (метод стохастического моделирования), метод построения модели векторной авторегрессии, метод параметрической коррекции обычными наименьшими квадратами, метод нечеткой логики (теории нечетких множеств).

Метод распределения вероятности случайной величины (метод Монте-Карло) основан на моделировании случайных процессов с заданными характеристиками, что позволяет с помощью генерации большого числа случайных выборок подбирать необходимое оптимальное значение. На основе данного метода осуществляется оценка будущих параметров с учетом предыдущих тенденций [20–22] (Momen, Mahyar and Shirinbakhsh, Mehrdad and Baniassadi, Amir and Behbahaninia, Ali, 2016; Paolo Brandimarte, 2014; Kovzunova, 2021). Так, в аспекте оценки продовольственной безопасности представляется возможным рассматривать динамику изменений индикаторов оценки в будущем как случайный процесс. В результате выполнения алгоритмов для каждого индикатора формируется набор значений по числу моделируемых реализаций в методе Монте-Карло, на основании которых осуществляется моделирование процентильных значений индикаторов в будущем [23, 24] (Svyatokho, 2016; Maslennikov, Mityakov, Kataeva, Fedoseeva, 2019). Усложняется использование метода необходимостью большого учета массива данных, обработку которого принято осуществлять с помощью компьютерного программирования.

В случае наличия усеченного количества данных представляется возможным использование модели векторной авторегрессии (VAR – Vector Autoregressive Model), позволяющей описывать действия совместно зависимых переменных через изменение своих значений предшествующих периодов и значений других совместно зависимых переменных. В VAR-моделях интерпретация оцениваемых параметров определяется структурой построенных уравнений. Данный метод позволяет измерять влияние факторов, заложенных в методику оценки продовольственной безопасности, и формировать тренды развития на будущую перспективу [25] (Kamenskiy, 2019), однако для более точных расчетов по данному методу требуются формализованные данные с меньшей степенью нечеткости. (VAR-модели применяются для систем прогнозирования взаимосвязанных временных рядов и для анализа динамического влияния возмущений (шоков) на систему выбранных показателей, то есть возможно применение в двух этапах алгоритма) [26–28] (Bekiro, Paccagnini, 2013).

При реализации оценки продовольственной безопасности по методике, включающей больший процент нечетких показателей, оптимальными являются методы теории нечетких множеств, например метод нечеткой (размытой) логики (Fuzzy-logic). Использование метода нечеткой логики теории нечетких множеств для построения модели оценки продовольственной безопасности макрорегиона позволяет оперировать нечеткими входными данными с нечеткой формализацией критериев оценки и сравнения. На основе метода нечеткой логики может быть построена нечетко-множественная модель оценки продовольственной безопасности макрорегиона. Данная модель представляет собой иерархическую взаимосвязь между входными переменными, группами входных переменных (критериями продовольственной безопасности макрорегиона) и выходной переменной (интегральным показателем продовольственной безопасности макрорегиона) [29–33] (Zvyagin, 2019; Lisitsyna, 2020; Wan Min, 2021; Gu, Wang, Xu, Chen, 2018; Lobova, 2015). С помощью данного метода возможно формирование «интервалов/порогов» для оценки продовольственной безопасности, а также осуществлять комплексную оценку продовольственной безопасности.

Для повышения точности результатов, достигнутых путем оценки продовольственной безопасности предшествующими методами, предусматривается использование метода параметрической коррекции обычными наименьшими квадратами – Parametric Corrected Ordinary Least Squares (COLS). Основной задачей метода является построение регрессионной модели границы эффективности и ее параллельный сдвиг до первой точки касания с одним из наблюдаемых значений, соответственно, объект, наблюдаемые значения которого находятся на границе эффективности, является эффективным, для остальных – отклонение от границы эффективности связано с неэффективностью [34] (Bryon Parman, Allen Featherstone, 2019). С помощью данного метода возможно осуществление оценки эффективности, под эффективностью можно понимать уровень продовольственной безопасности или продовольственной независимости [35].

С авторской точки зрения, учитывая особенности предложенной методики оценки продовольственной безопасности макрорегиона, оптимальным методом математического моделирования для проверки значимости показателей является метод Монте-Карло. Процедуру проверки методом Монте-Карло можно представить в виде следующей последовательности:

1. Устанавливается взаимосвязь между исходными данными (критерии оценки продовольственной безопасности) и выходным показателем (интегральным) в виде математической модели (Формула (1)). На данном этапе вводятся параметры модели, которые будут являться случайными величинами.

2. Задаются законы распределения вероятностей для ключевых параметров модели. При необходимости учитывается, что некоторые параметры модели являются коррелированными. Законы распределения задаются самостоятельно.

3. Проводится компьютерная имитация значений ключевых параметров модели на основе использования специального программного обеспечения.

4. Рассчитываются основные характеристики распределений исходных и выходных показателей. Проверяется гипотеза о значимости частного показателя в модели оценки.

5. Проводится анализ полученных результатов, принимается решение о включении показателя в оценку продовольственной безопасности макрорегиона.

Заключение

Таким образом, разработанная авторами методика оценки продовольственной безопасности макрорегиона позволяет осуществить комплексный анализ с учетом специфических особенностей территорий. Выводы, которые будут получены в результате проведения оценки критериев и показателей, позволят определить узкие места в системе обеспечения продовольственной безопасности макрорегиона и, как результат, определить основные векторы для разработки корректировочных мероприятий по совершенствованию ее инструментов.

Предложенный подход позволил расширить перечень частных показателей оценки, включив необходимые критерии, значимые для оценки продовольственной безопасности, такие как транспортная доступность, безопасность продовольствия, устойчивость продовольственной системы. Исключение балльно-рейтинговой системы из процесса формирования интегрального показателя позволяет нивелировать выявленные недостатки существующих отечественных и зарубежных подходов к оценке через снижение уровня субъективности полученных результатов. Включение методов математического моделирования предоставляет новые возможности для получения релевантных результатов с учетом неопределенности внешней среды и количественных показателей, что, в свою очередь, является базой для гибкого реагирования на изменяющиеся условия. Использование комбинации методов ориентировано на более точные расчеты за счет корректировки субъективности значений нечетких параметров, включенных в оценку продовольственной