Эконометрическое моделирование сборов фандрайзингового благотворительного фонда «Русфонд» в системе социально-экономической безопасности

Введение

Актуальность теоретических основ благотворительности. В первую очередь необходимо рассмотреть сущность изучаемого явления – благотворительности. Согласно Федеральному закону «О благотворительной деятельности и добровольчестве (волонтерстве)» [1], «благотворительная деятельность – это добровольная деятельность граждан и юридических лиц по бескорыстной (безвозмездной или на льготных условиях) передаче гражданам или юридическим лицам имущества, в том числе денежных средств, бескорыстному выполнению работ, предоставлению услуг, оказанию иной поддержки».

Приказом Минэкономразвития России «О Координационном совете по вопросам развития благотворительной деятельности» [2] утверждены задачи Совета в следующем контексте:

- координация работы по реализации мер по содействию развитию благотворительности в Российской Федерации (содействует «реализации государственных программ и национальных проектов в системе социально-экономической безопасности России» [6] (Karavaeva, Bukhvald, Soboleva, Kolomiets, Lev, Ivanov, Kazantsev, Kolpakova, 2019));

- содействие в реализации Концепции, Плана мероприятий по реализации

Концепции, Плана мероприятий по популяризации благотворительности.

Для решения возложенных задач Совет осуществляет следующие функции:

- обеспечение взаимодействия благотворительных и коммерческих организаций, ответственных за реализацию благотворительных программ и проектов;

- «обобщение и содействие в обмене опытом работы по реализации федеральными органами исполнительной власти и заинтересованными организациями Концепции» [11] (Lev, Medvedeva, Leshchenko, Perestoronina, 2021), Плана мероприятий по реализации Концепции, Плана мероприятий по популяризации благотворительности;

- подготовку предложений по вопросам формирования и осуществления государственной политики по развитию благотворительности в Российской Федерации;

- подготовку предложений по проектам нормативных правовых актов по вопросам развития благотворительности в Российской Федерации;

- выработку рекомендаций по проведению мониторинга и оценки эффективности мер, направленных на развитие благотворительности в Российской Федерации.

В целях реализации указанных задач и функций Совет:

- запрашивает и получает в установленном порядке от федеральных органов исполнительной власти и заинтересованных организаций информацию по вопросам развития благотворительности;

- «готовит предложения по вопросам формирования и осуществления социально-экономической политики по развитию благотворительности» [7] (Lev, 2021).

Одним из основных способов осуществления благотворительной деятельности в России являются благотворительные организации – неправительственные (негосударственные и немуниципальные) некоммерческие организации, созданные для реализации целей благотворительной деятельности. Одной из таких благотворительных организаций является рассматриваемый в работе фонд – «Русфонд».

По своей экономической сути благотворительность есть ничто иное как направление частными лицами собственных материальных ресурсов в пользу лиц, которые крайне в них нуждаются в силу различных причин [9, с. 213]. Рост роли благотворительности в финансировании, в решении многих социальных проблем является одной из основных тенденций развития общества во многих странах мира, в том числе и в России. Сам факт существования благотворительности как некоего института перераспределения благ в интересах общества, функционирующего отдельно от государства, позволяет обществу достигать более быстрого социально-экономического развития, которое будет тем выше, чем эффективнее будет работать институт благотворительности [9, с. 213] (Sivolap, 2019, р. 213). В свою очередь, эффективность этого института напрямую зависит от эффективности реализующих благотворительность лиц – благотворительных организаций.

«Русфонд» (Российский фонд помощи) – один из крупнейших благотворительных фандрайзинговых фондов России. Создан в 1996 году как благотворительная программа Издательского дома «Коммерсантъ» для оказания помощи авторам отчаянных писем в газету «Коммерсантъ» [3, с. 2] (Klishina, Logvinenko, 2017, р. 2).

Как уже было упомянуто ранее, «Русфонд» (как и многие другие благотворительные организации в России) получает финансирование посредством фандрайзинга. В широком смысле фандрайзинг – целенаправленная стратегия привлечения различных ресурсов, которые организация не в силах обеспечить самостоятельно, с применением актуальных маркетинговых инструментов, методов и технологий [10], однако в российской практике закрепилось другое понимание данного понятия: фандрайзинг – способ привлечения ресурсов для реализации благотворительных проектов и программ [5, с. 60] (Korneeva, Bryukhno, 2019, р. 60).

В целом в алгоритме ведения фандрайзингового проекта можно выделить следующие этапы [10]:

- донесение информации о деятельности организации, ее потребностях и ключевой миссии проекта до потенциальных спонсоров (доноров);

- определить целевую аудиторию проекта, в сердцах которой деятельность компании находит особый отклик, получить от нее необходимые ресурсы;

- заинтересовать в регулярных пожертвованиях во благо продвижения деятельности проекта.

Таким образом, можно справедливо считать, что доходы фондов фандрайзингового типа (в том числе «Русфонда») сложно назвать стабильными и предсказуемыми, так как они зависят от возможности и желания людей жертвовать деньги. Более того, пожертвования в пользу благотворительных фондов во многих случаях совершаются спонтанно, единоразово. В то время как финансовая устойчивость – ключевой элемент эффективной деятельности некоммерческих организаций [4, с. 49], обеспечение которой невозможно без финансового планирования, включающего планирование притоков и оттоков денежных средств. Поэтому прогноз доходов фандрайзингового фонда является весьма актуальной задачей, так как это способствует повышению эффективности деятельности таких фондов, что положительно сказывается на социально-экономическом развитии страны.

Оценка первоначального вида модели по исходной выборке

В рамках данной работы предлагается проверить адекватность модели временного ряда доходов фандрайзингового благотворительного фонда Русфонд.

Предполагаемый вид спецификации модели:

(1)

Данный вид спецификации составлен, основываясь на диаграмме рассеивания месячных сборов «Русфонда» за 2014–2019 гг. (рис. 1).

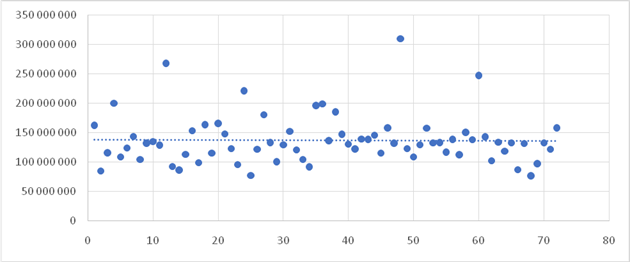
Рисунок 1. Диаграмма рассеивания месячных сборов «Русфонда» за 2014–2019 гг. Источник: построена автором по исследуемым материалам [8].

Параметры модели можно экономически интерпретировать следующим образом:

1) а₀ – ожидаемые сборы «Русфонда» в декабре. В рамках предложенной спецификации (1) именно декабрь взят в качестве базового периода, который в дальнейшем корректируют фиктивные переменные;

2) а₁ – предельное изменение эндогенной переменной по фактору времени t. Если данный параметр принимает значение больше нуля, то с течением времени эндогенная переменная будет увеличиваться в среднем на величину оценки параметра а₁. Если он будет меньше нуля, то все будет ровно наоборот;

3) параметры а₃-а₁₂ – это предельное изменение эндогенной переменной в месяце, отличном от базового (декабрь), в сравнении с базовым.

Можно заметить, что сборы примерно равномерно располагаются вокруг прямой. Более того, можно наблюдать цикличность, а также схожие значения в аналогичных месяцах разных годов. Например, во многих годах декабрь был месяцем с самыми высокими сборами. По этой причине было решено попробовать специфицировать модель с месячным влиянием. Уже на этом этапе стоит отметить, что на диаграмме рассеивания не прослеживается ни восходящей, ни нисходящей тенденции, то есть влияние фактора t, отвечающего за влияние тенденции, может оказаться незначительным либо вообще отсутствовать.

Оценку модели предлагается проводить посредством схемы Гаусса-Маркова, то есть используя метод наименьших квадратов. Данный метод можно использовать, так как (1) – модель множественной регрессии. В общем виде данный метод выглядит следующим образом:

;	(2)
;	(3)
;	(4)
,	(5)

где X – матричная запись уравнений наблюдений, расширенная единичным столбцом,

– вектор наблюдаемых значений эндогенной переменной,

q – элементы квадратной обратной матрицы .

Данный метод дает оптимальные оценки параметров лишь в том случае, когда выполняется ряд условий:

	(6)
	(7)
≠j	(8)
	(9)

Таким образом, необходимо не только оценить модель, используя заявленный метод, но и проверить, выполняются ли предпосылки 6–9.

В качестве контрольной выборки для дальнейшей проверки адекватности рассматриваемой модели решено взять сборы за январь и февраль 2014 года, ноябрь и декабрь 2019 года.

В результате оценки модель (1) понимает следующий вид:

(10)

На данном этапе стоит обратить внимание на то, что все стандартные отклонения оцененных параметров являются эффективными (разрядность ошибок ниже разрядности оцененного параметра) за исключением параметра и его оценки при t, где разрядность ошибки выше разрядности оцененного параметра.

Далее необходимо проверить предпосылки теоремы Гаусса-Маркова (6)–(9).

Предпосылка (6) проверяется с использованием коэффициента детерминации R² и F-теста. В данном случае R² = 0,63, а наблюдаемая F-статистика = 7,7. F критическое, рассчитанное на уровне значимости 0,05, равняется 1,93, то есть наблюдаемое значение F-статистики выше критического, значит, наблюдаемому значению R² можно доверять и судить о том, что выбранные регрессоры объясняют эндогенную переменную на 63%, то есть они обладают средней объясняющей способностью. Результаты проведенного теста также позволяют говорить о том, что предпосылка (6) выполняется.

Предпосылка (7) о гомоскедастичности случайных остатков проверяется посредством теста Голдфельда-Квандта. В рамках данного теста необходимо упорядочить уравнения наблюдений по возрастанию суммы модулей значений регрессоров, затем разделить полученную выборку на 3 примерно равные части n’ (чтобы выполнялось условие k+1<n’), затем по двум крайним выборкам посчитать ESS и с их использованием посчитать статистику:

(11)

Проведя все вышеперечисленные процедуры в рамках рассматриваемой модели, можно получить статистику GQ = 1,37. Далее необходимо посчитать значение 1/GQ и F критическое, а также сравнить полученные значения GQ и 1/GQ с F критическим. В данном случае имеем 1/GQ = 0,73 и F критическое = 2,98 на уровне значимости 0,05. Видно, что выполняются следующие неравенства:

(12)

Следовательно, можно судить о том, что предпосылка о гомоскедастичности случайных остатков в модели выполняется.

При проверке предпосылки (8) необходимо провести тест Дарбина–Уотсона, суть которого заключается в расчете статистики DW (12), а также в определении промежутка, в который попадает наблюдаемая статистика (рис. 2).

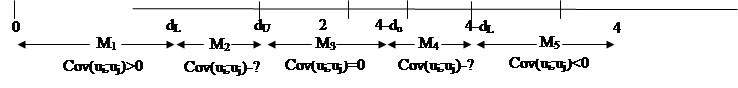
Рисунок 2. Отрезок Дарбина-Уотсона

(13)

Проведя все необходимые вычисления, получаем наблюдаемую статистику DW в размере 2,21. Используя таблицу, составленную Дарбином и Уотсоном, найдем ближайшие значения d_U и d_L. В связи с тем, что в таблице отсутствуют значения для n = 68 (объем обучающей выборки) и к = 12 (количество регрессоров), возьмем две ближайшие пары значений:

1) для n = 65 и k = 12 имеем значения d_U = 1,889 и d_L = 1,053, 4-d_U = 2,111 и 4-d_U = 2,947;

2) для n = 70 и k = 12 имеем значения d_U = 1,87 и d_L = 1,099, 4-d_U = 2,13 и 4-d_U = 2,901.

В обоих случаях наблюдаемая статистика DW попадает в промежуток М₄, что является зоной неопределенности. Однако можно заметить, что в обоих случаях статистика ближе именно к левой границе интервала, что говорит о том, что предпосылка (8) скорее выполняется, чем нет.

Далее, убедившись, что все предпосылки теоремы Гаусса-Маркова выполняются, и следовательно, убедившись, что полученные оценки являются оптимальными, необходимо провести проверку адекватности модели, используя метод интервального прогнозирования.

В рамках данного метода нужно рассчитать стандартную ошибку прогноза (14), а также нормированную ошибку прогноза t_крит и на их основе рассчитать интервальный прогноз [y₀^-; y₀⁺].

	(14)
	(15)
	(16)
	(17)

Проведя все расчеты (14)–(16) для каждого значения из контрольной выборки, можно получить следующие результаты:

1. Прогнозный интервал для января 2014 года: [52 466 396; 179 248 159] при фактическом значении 162 498 659.

2. Прогнозный интервал для февраля 2014 года: [59 051 437; 185 833 200] при фактическом значении 84 837 330.

3. Прогнозный интервал для ноября 2019 года: [73 548 859; 200 330 623] при фактическом значении 121 836 530.

4. Прогнозный интервал для декабря 2019 года: [184 582 458; 311 364 221] при фактическом значении 158 333 787.

Таким образом, можно судить о том, что модель (10) является адекватной в 75% случаев на уровне значимости 0,05, так как фактические значения эндогенной переменной из контрольной выборки принадлежат прогнозным интервалам в 3 из 4 случаев.

Проверка типовых ошибок в спецификации модели

Первая типовая ошибка в спецификации заключается в выборе ошибочного вида типа функции регрессии. Для выявления наличия этой оценки необходимо проверить ее симптомы:

1. Диаграмма рассеивания (рис. 1) из всех возможных вариантов более всего напоминает именно линейную функцию, поэтому автор считает, что первого симптома первой ошибки не наблюдается.

2. Второго симптома, по мнению автора, также не наблюдается, так как отсутствует длительное постоянство знаков случайного остатка.

3. 3-й симптом явно наблюдается, так как разница между оценками параметров, рассчитанных по двум одинаковым частям уравнений-наблюдений, является значительной, разница между параметрами выходит за рамки их ошибок.

Найден лишь один симптом ошибки первого типа, поэтому гипотеза о наличии данной ошибки отвергается.

Вторая типовая ошибка в спецификации модели заключается во включении в функцию регрессии незначащей переменной. Для выявления наличия данной ошибки необходимо проверить значимость регрессоров по t-критерию. Другими словами, необходимо для каждого параметра модели проверить справедливость неравенства (18). Если неравенство оказывается справедливым, то параметр (и регрессор при нем) признается незначащими.

(18)

Результаты расчетов показывают, что t (регрессор, отражающий момент времени) и параметр a₁ при этом регрессоре признаются незначащими. Это было ожидаемо, так как в предыдущем разделе упоминалось, что на диаграмме рассеивания (рис. 1) не прослеживается ни восходящей, ни нисходящей тенденции. Более того, ошибка параметра a₁ ранее также признавалась неэффективной по критерию соотношения разрядности среднеквадратичной ошибки параметра с его значением.

Третья типовая ошибка в спецификации модели заключается в пропуске какого-либо значащего критерия и невключении его в модель. Данная ошибка уже была проверена в прошлом разделе посредством теста Дарбина-Уотсона, который показал, что автокорреляция случайных остатков скорее отсутствует, что указывает на то, что никакого реально значащего регрессора скорее не упущено.

Четвертая ошибка заключается в оценивании модели по выборке, считая, что изучаемый экономический процесс/объект/явление ведет себя одинаково на всем протяжении наблюдения, однако это не всегда верно, ведь порой закономерности, условия существования процесса/объекта/явления могут меняться со временем, и следовательно, будут меняться оценки параметров или даже сама модель. При взгляде на диаграмму рассеивания (рис. 1) можно наблюдать, что сначала амплитуда колебаний значений была выше, чем примерно с момента времени t = 40, далее амплитуда становится меньше и цикличность становится более заметной. Таким образом, выдвигается гипотеза о наличии структурного сдвига в момент времени t = 40. Проверить это можно через тест Чоу, который заключается в оценивании модели по всей выборке, по выборке до структурного сдвига и после структурного сдвига, расчете z-статистки (19), расчете F критического, а также выполнимости проверки неравенства (20).

	(19)
	(20)

Результат расчетов (z = 7,7, F_кр = 1,96 на уровне значимости 0,05) позволяет констатировать факт наличия структурного сдвига в момент времени t = 40 (апрель 2017 года). Более того, можно наблюдать тот факт, что спецификация (1) является некачественной для выборки до структурного сдвига (в этом случае R² = 0,58), но она является качественной (более того, регрессоры обладают весьма высокой объясняющей способностью исходя из R² = 0,9) для выборки после структурного сдвига. При этом для данной выборки все ошибки можно назвать эффективными, и даже регрессор t, признанный ранее незначащим, в данном случае является значащим. Предлагается рассмотреть спецификацию модели (1) в отношении выборки после структурного сдвига, приняв ее первое значение за t = 1.

Оценка модели с учетом выявленного структурного сдвига

В результате проведения тех же операций, что и в разделе, посвященном оценке первоначального вида модели, полученная оцененная модель (21) является оптимальной, более качественной, чем модель (10), но при проверке адекватности также была осечка: результат декабря 2019 года также не удалось спрогнозировать (фактическое значение – 155 333 787, прогнозный интервал – [209 343 545;308 354 804]), прогноз же по ноябрю 2019 года оказался успешным (фактическое значение – 121 836 530, прогнозный интервал – [65 659 537;164 670 795]).

(21)

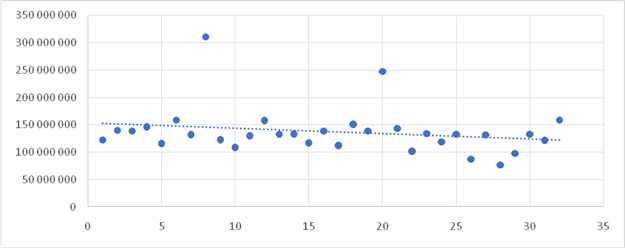
Рисунок 3. Диаграмма рассеивания выборки после структурного сдвига

в апреле 2017 года

Источник: составлено автором.

При взгляде на диаграмму рассеивания выборки после структурного сдвига (рис. 3) и сравнении ее с первоначальной диаграммой рассеивания (рис. 1) можно наблюдать более явную нисходящую тенденцию (именно в связи с этим в модели (21) регрессор t является значащим, в отличие от модели (10). Также хочется обратить внимание на три точки (t = 8, t = 20, t = 32), которые показывают декабрьские сборы. Можно заметить, что у них наблюдается серьезная нисходящая тенденция, их значения весьма сильно друг от друга отличаются, что, по мнению автора, негативно сказывается на оценке вида модели, а также является причиной неудачи в прогнозировании сборов декабря 2019 года по оцененному виду (21).

Заключение

В работе была исследована модель временного ряда месячных сборов «Русфонда». Было выявлено, что изначально предложенная спецификация, оцененная по первоначальной выборке, является адекватной в 75% случаев, ее регрессоры обладают средней объясняющей способностью. Однако нельзя сказать, что данная модель реально пригодна для использования на практике, потому что:

- при ее спецификации совершен ряд ошибок;

- проверка адекватности показала, что истинное значение не всегда попадает в прогнозный интервал. Более того, сам по себе прогнозный интервал является очень широким, что говорит о достаточно низкой точности прогноза, которая не может удовлетворить потребности фонда в точном прогнозе его денежных притоков.

Объясняющая способность регрессоров хоть и является приемлемой в теории, но на практике следует искать модели, более полно объясняющие эндогенную переменную – месячный доход фонда.

При анализе модели на наличие структурных сдвигов был обнаружен таковой. Более того, оказалось, что изначальная модель оказалась качественной в большей степени из-за того, что данной моделью хорошо объясняется именно часть выборки после структурного сдвига (R² = 0,9), в то время как для выборки до структурного сдвига модель не является качественной и не может быть никак использована.

Использование модели для выборки после структурного сдвига теоретически, по мнению автора, можно назвать целесообразным, несмотря на то, что одно из двух значений контрольной выборки она все-таки не смогла предсказать. Это связано лишь с отличающейся от прочих месяцев динамикой сборов в декабре. Однако стоит отметить, что для оценивания модели была использована слишком малая выборка, поэтому полностью доверять полученным результатам не стоит, а значит, применение модели на практике также не является целесообразным. Более того, прогнозные интервалы даже при оценке модели после структурного сдвига являются довольно широкими, что также заставляет усомниться в целесообразности ее использования в реальной практике.

Также необходимо отметить, что проверка обеих рассмотренных моделей (по всей выборке и по выборке после структурного сдвига) на наличие автокорреляции случайного остатка не дает однозначного результата, так как проведенный тест Дарбина-Уотсона указывает на неопределенность, поэтому результаты обеих оценок вызывают еще большие сомнения.

В целом можно сказать, что при более глубоком изучении практики сборов благотворительного фонда, например в разрезе конкретных источников поступления, регулярности их поступления, можно составить более точную спецификацию модели. Также отсутствие достаточного объема статистики по сборам после выявленного структурного сдвига является проблемным моментом. Возможно, большее число наблюдений положительно скажется на рассмотренной в работе модели временного ряда и позволит в том числе учесть выпадающее из общей массы поведение сборов в декабре, сделает ее более точной с точки зрения прогнозов по каждому месяцу.