Построение системы показателей по предпринимательству в Российской Федерации и их прогнозирование на основе интеллектуальной гибридной системы «Горизонт»

Введение

В Указе Президента Российской Федерации «О национальных целях развития Российской Федерации на период до 2030 года» говорится о целеполагании в отношении осуществления прорывного развития страны [1]. Одной из национальных целей является «Достойный, эффективный труд и успешное предпринимательство». Целевые показатели, характеризующие достижение данной цели, отражают фокусирование государственной власти на развитии предпринимательской среды, обеспечении темпа роста валового внутреннего продукта, увеличении доходов и занятости населения. Проводником достижения данных показателей является малое и среднее предпринимательство. Малое и среднее предпринимательство как субъект новой рыночной экономики в значительной степени определяет структуру взаимоотношений элементов экономической системы, увеличивает общий объем валового внутреннего продукта, укрепляет производство и розничный товарооборот, развивает экономическую базу регионов, обеспечивает занятость населения, а также создает условия для развития конкурентной среды, побуждая к научно-техническим инновациям.

В этой связи прогнозирование развития малого и среднего предпринимательства является важной задачей для крупных субъектов рыночной экономики. Оно не только сокращает время оперативного принятия управленческих решений, но и способствует повышению конкурентоспособности малого и среднего предпринимательства.

Объект исследования – малое и среднее предпринимательство в Российской Федерации.

Предмет исследования – методы и модели прогнозирования показателей по предпринимательству в Российской Федерации.

Цель исследования – разработка краткосрочного прогноза показателей предпринимательства в Российской Федерации на основе комплексной прогнозной модели, реализованной в интеллектуальной гибридной системе «Горизонт».

Актуальность исследования обусловлена повышенным вниманием к малому и среднему предпринимательству со стороны государственного управления и общественных институтов. В постоянно меняющихся политических и экономических условиях оперативное прогнозирование и моделирование изменчивой внешней среды позволяет малому и среднему предпринимательству приспосабливаться к новым условиям существования гораздо легче и с меньшими издержками. Экономико-математическое обеспечения предпринимательской деятельности является не только предметом интереса со стороны государства при планировании и проведении долгосрочных программ развития, но и для самих предприятий малого и среднего бизнеса является важным и необходимым средством, помогающим в достижении внутренних целей. Один из возможных вариантов такого обеспечения на краткосрочную перспективу предлагается в данном исследовании.

Предпринимательство принято делить на малое, среднее и крупное. Каждая из этих форм существования организации обладает собственными закономерностями существования и развития, качественными и количественными различиями и степенью участья в социально-экономической жизни страны. В рамках настоящей статьи рассматривается малое и среднее предпринимательство как наиболее многочисленный класс, обладающий, в отличие от крупного предпринимательства, меньшим запасом устойчивости, а потому требующий повышенного внимания и поддержки со стороны государственного управления. Согласно статье 4 ФЗ «О развитии малого и среднего предпринимательства в Российской Федерации», к субъектам малого и среднего предпринимательства относятся юридические, а также физические лица, соответствующие следующим условиям [2]:

1) Суммарная доля участия Российской Федерации, субъектов Российской Федерации, муниципальных образований, иностранных и прочих юридических лиц в уставном капитале не должна превышать 25%.

2) Средняя численность работников до 100 человек для малых предприятий и от 100 до 250 для средних.

3) Выручка от реализации товаров, работ, услуг без учета налога на добавленную стоимость не должна превышать 800 млн. руб. для малых предприятий и 2 млрд. руб. для средних предприятий.

По данным государственной статистики на начало 2022 года в России насчитывалось 212 429 субъектов малого предпринимательства и 17 977 субъектов среднего [8].

Основными характеристиками малого и среднего предпринимательства являются:

1. Организационно-технологическая гибкость, которая позволяет при необходимости своевременно реагировать на изменение рыночной конъюнктуры и оптимизировать состав активов.

2. Успешная предпринимательская деятельность на региональных рынках сбыта благодаря использованию местных ресурсов и лучшему пониманию структуры и особенностей экономических отношений регионального уровня.

3. Способность оперативно реагировать на изменения спроса потребителей благодаря непосредственному и постоянному контакту с ними.

4. Высокий уровень адаптивности и готовность к научно-техническим инновациям.

5. Гибкость и оперативность в принятии управленческих решений.

6. Необходимость относительно небольшого капитала на старте предпринимательской деятельности и малый срок оборота активов, в том числе денежных средств.

Исходя из указанных характеристик малого и среднего предпринимательства можно обозначить его важнейшую функцию, которая заключается в содействии перестройке структуры взаимоотношений элементов экономической системы, в ходе которой субъекты малого и среднего предпринимательства своей деятельностью компенсируют недостаточную гибкость крупных предприятий и их реакцию на изменения потребительского спроса. Как было отмечено ранее, малое и среднее предпринимательство увеличивает общий объем валового внутреннего продукта, укрепляет производство и розничный товарооборот, развивает экономическую базу регионов, обеспечивает занятость населения, а также создает условия для развития конкурентной среды, побуждая к научно-техническим инновациям [2].

Таким образом, малое и среднее предпринимательство по совокупности факторов в значительной степени влияет на социально-экономическое благополучие России, а потому требует повышенного внимания и поддержки со стороны государственного управления.

ОСНОВНАЯ ЧАСТЬ

Модель показателей для социально-экономического прогнозирования

Прогнозирование является одной из составных частей государственного регулирования экономики и позволяет принимать обоснованные управленческие решения, особенно в нестабильной ситуации. С помощью методов и инструментов экономико-математического моделирование достигается качество построенного прогноза и соответствие принимаемых на его основе управленческих решений целям, реализуемым в рамках экономической политики.

В основе такого подхода комплексного рассмотрения процессов экономического развития в рамках единой модели лежит эконометрическая модель национальных экономик, разработанная американским экономистом Лоуренсом Клейном [3]. В России развитие описанного подхода также имело практические результаты, основные модели описаны в работах [4-6].

Разработка новой большой страновой эконометрической модели экономики Российской Федерации была начата в 2013 году научным коллективом кафедры информатики РЭУ им. Г.В. Плеханова [7]. В ее основе лежит авторская методология построения распределенной системы расчетов кратко и среднесрочного прогноза показателей социально-экономического развития, включающей показатели макроэкономики, финансовой, инновационной и социальной сфер деятельности (построение системы регрессионных уравнений) во взаимосвязи с динамикой основных макроэкономических показателей. В построенной системе регрессионных уравнений каждый показатель определяется как функция других показателей в соответствии с экономическим смыслом, а также строится соответствующая единая распределенная система уравнений. Пошаговое параллельно-последовательное решение исследуемых уравнений позволяет получать взаимосвязанные прогнозы показателей в зависимости от задаваемых сценарных условий, представляющих собой варианты развития внешних показателей.

В модель входят блоки показателей, характеризующих различные сферы экономической системы страны [7, 9-12]. Авторами настоящего исследования разработан новый блок показателей по предпринимательству.

Блок экспертных показателей вариантов сценарных условий прогноза включает в себя показатели ключевой ставки Банка России, темп прироста денежной массы в национальном распределении, цены на нефть марки Urals, изменение международных резервов Российской Федерации. Сценарные условия задают предполагаемую траекторию развития экономики Российской Федерации [8].

В построенной страновой модели сценарные показатели являются факторными переменными, благодаря которым осуществляется расчет входящих в модель результативных переменных.

В блок макроэкономических показателей выведены наиболее значимые и чаще используемые в качестве аргументов показатели. Эти показатели рассчитываются в первую очередь для того, чтобы в уравнениях всех других показателей была возможность использовать текущие значения найденных аргументов [9].

На основе рассчитанных сценарных и макроэкономических показателей рассчитываются показатели остальных блоков модели. Таким образом, формируется единая модель взаимоувязанных показателей всех сфер экономики, которая позволяет осуществлять макроэкономическое прогнозирование.

Структура системы показателей по предпринимательству в Российской Федерации

Все отобранные в систему показатели должны быть взаимоувязаны по экономическому смыслу и подразделяться на уровни и блоки. Для прогнозирования показателей по предпринимательству были отобраны показатели, характеризующие различные аспекты успешности предприятия. Всего было сформированы четыре блока показателей (рисунок 1).

Рис. 1. Структура исследуемых показателей предпринимательства

Источник: разработано авторами

В общей сложности в работе используется 14 показателей, которые разделены на 4 блока. В качестве источников информации использованы официальные данные государственной статистики.

Таблица 1

Показатели по предпринимательству

Построенный блок показателей по предпринимательству дополняет модель социально-экономических показателей Российской Федерации, тем самым расширяя возможности ее применения для решения практических задач краткосрочного прогнозирования.

Гибридная система прогнозирования «Горизонт»

Как было показано ранее, одним из самых распространенных методов прогнозирования социально-экономических показателей является линейная регрессия. Однако, несмотря на свою широкую применимость и высокую описательную способность, данный метод имеет ряд ограничений. В частности, полученные с помощью линейных регрессионных уравнений оценки могут не быть точными, если между показателями имеется нелинейная связь, или подаваемые на вход отчетные данные неполные или несопоставимые между собой. Это означает, что при прогнозировании социально-экономических показателей развития Российской Федерации возможна ситуация, при которой для части показателей построенный прогноз является неудовлетворительным с точки зрения качества и точности.

Решить данную проблему могут интеллектуальные методы анализа данных, которые менее требовательны к качеству первоначальных отчетных данных и способны моделировать нелинейные зависимости. Качественное решение задач прогнозирования должно осуществляться за счет применения гибридного подхода к анализу данных, который сочетает классические методы регрессионного анализа и интеллектуальные методы [10-12]. Гибридный подход был реализован авторами в системе гибридных моделей «Горизонт». Система «Горизонт» является аналитической системой с возможностью прогнозирования с использованием различных моделей машинного обучения [12]. В настоящий момент в рамках системы функционируют основные модули:

· Модуль загрузки данных;

· Модуль построения регрессионных уравнений;

· Модуль построения искусственных нейронных сетей;

· Модуль построения регрессионных деревьев решений (CART).

Система имеет микросервисную архитектуру, что обуславливает ее масштабируемость с точки зрения разрабатываемых сервисов (модулей). В данной системе реализована авторская методология кратко- и среднесрочного прогнозирования социально-экономических показателей на основе регрессионных линейный уравнений. Для тех показателей, по которым были получены неудовлетворительные значения прогноза в системе «Горизонт» реализованы модули интеллектуального анализа (нейронные сети и деревья решений).

В системе «Горизонт» выделяются балансово-эконометрические модели на основе линейной регрессии и интеллектуальные модели, включающие нейросетевые модели и деревья решений.

Работа в системе «Горизонт» состоит из следующих последовательных этапов:

1) Сбор, первичная подготовка и загрузка отчетных данных по исследуемым показателям. Основным требованием к первоначальному набору данных является отсутствие пропущенных значений.

2) Для загруженного набора данных проводится корреляционный анализ для установления линейных зависимостей между показателями. Результаты анализа представляются в виде матрицы корреляций.

3) На основе корреляционного анализа и экономического смысла в рамках разработанной методологии прогнозирования задаются последовательные линейные зависимости между всеми показателями (строится система линейных уравнений).

4) Выбираются сценарные показатели и задаются условия прогноза.

5) Проводится расчет системы линейных уравнений на основе метода наименьших квадратов.

6) Проводится верификация построенных регрессионных моделей. Строится матрица верификации.

7) Показатели с неудовлетворительными результатами прогноза проходят повторный расчет в блоке интеллектуальных моделей.

8) Результаты расчетов с использованием гибридного подхода визуализируются и выводятся в табличной форме.

В настоящей статье для прогнозирования показателей предпринимательства наряду с регрессионными моделями использовались модели регрессионных деревьев решений и случайного леса и нейросетевые модели.

Регрессионный анализ

Характерной особенностью экономических явлений является то, что они определяются большим количеством одновременно действующих факторов. Установление правильных взаимосвязей факторов и явлений способствует верному определению экономических целей и средств их достижения. В рамках данного подхода ставится задача исследования зависимостей одной переменной y от набора влияющих на нее переменных x_m. Нахождение такого рода зависимостей выполняется с помощью методов регрессионного анализа, в частности линейного.

Линейная регрессия является самым распространённым методом регрессий, так как ее результаты легко интерпретируются. Качество построенных моделей регрессии определяется с помощью коэффициента детерминации R². Для оценки точности регрессионных моделей используется средняя относительная ошибка прогнозирования МАРЕ. Значимость построенной модели определяется по F-критерию Фишера. Для оценки меры автокорреляции отклонения отчетной и регрессионной функций на исследуемом промежутке применяется критерий Дарбина–Уотсона DW.

Однако, несмотря на свою широкую применимость и высокую описательную способность, данный метод имеет ряд ограничений. В частности, полученные с помощью линейных регрессионных уравнений оценки могут не быть точными, если между показателями имеется нелинейная связь, или подаваемые на вход отчетные данные неполные или несопоставимые между собой. Это означает, что при прогнозировании социально-экономических показателей развития Российской Федерации возможна ситуация, при которой для части показателей построенный прогноз является неудовлетворительным с точки зрения качества и точности.

Решить данную проблему могут интеллектуальные методы анализа данных, которые менее требовательны к качеству первоначальных отчетных данных и способны моделировать нелинейные зависимости.

Модели деревьев решений и случайного леса

Деревья решений наравне с моделями регрессии используются для определения статистических взаимосвязей нескольких переменных, одна из которых определяется как зависимая от других. Значимым различием между деревьями решений и моделями регрессии является то, взаимосвязь показателей в деревьях решений выражается не в виде прогнозного уравнения, а в виде древовидной иерархической структуры. Согласно иерархии дерева решений, первоначальный набор данных для анализа называется корневым узлом, который затем разбивается на несколько новых узлов таким образом, чтобы данные в каждом из новых узлов максимально различались друг с другом по зависимой переменной. Правила разбиения данных задаются по значениям независимых переменных. Такие правила содержатся на ветвях дерева, которые соединяют разбиваемые узлы друг с другом. Каждый новый узел дерева решений затем также разбивается на узлы. Разбиение продолжается до тех пор, пока не перестанут улучшаться статистические значения, характеризующие взаимосвязь показателей. После завершения всех разбиений подсчитывается среднее значение зависимой переменной по всем узлам. Данный процесс разделения исходного набора данных называется рекурсивным. Построенная в результате разделения иерархическая структура называется деревом решений и содержит описательные статистики характера взаимосвязей значений зависимой переменной и независимых. Для прогнозирования среднего значения количественной зависимой переменной от независимых переменных используются деревья регрессии.

Недостатком использования метода деревьев решений является то, что они склонны к переобучению и показывают нестабильные результаты, когда внесение небольших изменений в первоначальный набор данных может приводить к полному изменению иерархической структуры дерева. Метод случайного леса был разработан как способ решения этой проблемы. В обобщенном виде случайный лес – это набор деревьев решений. Суть метода заключается в усреднении результатов обучения каждого отдельного дерева в наборе. Для того, чтобы построить модель случайного леса, сначала необходимо определить количество деревьев. Совокупность деревьев, входящих в модель случайного леса, называется ансамблем деревьев. Каждое дерево должно на приемлемом уровне прогнозировать зависимую переменную и отличаться от других деревьев. Для этого в процесс построения деревьев вносится случайность, которая должна обеспечивать уникальность каждого дерева. Для получения рандомизированных деревьев в случайном лесу последовательно применяются две техники: сначала случайным образом отбираются наблюдения, которые будут использоваться для построения дерева, а затем случайно отбирается определенное количество предикторов в каждом разбиении. Таким образом формируются бутстреп-выборки (bootstrap sample) – из набора данных с n наблюдениями случайным образом выбираются наблюдения с возвращением n раз [13, 14]. В итоге получается выборка, которая имеет такой же размер, что и исходный набор данных, однако некоторые наблюдения будут отсутствовать в нем, а некоторые попадут в него несколько раз.

Случайный лес обладает возможностью оценивать важность отдельного предиктора с точки зрения улучшения прогнозирования. Мерой важности предиктора выступает усредненное уменьшение неоднородности. В деревьях регрессии оценивается уменьшение разброса значений зависимой переменной относительно определенного среднего значения в узлах-потомках. Для этого используется внутриузловая дисперсия.

Несмотря на то, что важность переменных несет ценную информацию, не меньший интерес представляет взаимосвязь предиктора с зависимой переменной. Метод частной зависимости основывается на прогнозах, получаемых с помощью случайного леса, и позволяет визуализировать взаимосвязь между зависимой переменной и предикторами. Поскольку случайный лес может аппроксимировать практически любую функциональную зависимость между откликом и предиктором, с помощью графика можно обнаружить нелинейные зависимости.

Использование случайного леса по сравнению с одиночным деревом решений дает лучшее качество модели за счет усреднения результатов по-разному переобучающихся деревьев. Другим преимуществом метода случайного леса является то, что случайный лес способен более точно оценить вклад и поведение каждого предиктора, даже когда эффект одного предиктора ослаблен более значимыми предикторами, что характерно для регрессионных моделей.

Искусственные нейронные сети

Базовой для решения задач регрессии является нейронная сеть, в которой присутствует хотя бы один скрытый слой. Такая сеть называется многослойным персептроном. В такой сети при подаче на вход вектора X = (x₁, x₂, … , x_n)^T многослойный персептрон сформирует на выходе вектор Y = (y₁;y₂)^T, значения элементов которого вычисляются по формуле:

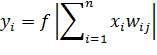, где

f – активационная функция,

i – номер нейрона входного слоя, с выхода которого выходит связь,

j – номер нейрона выходного слоя, на вход которого поступает связь.

Для настройки нейронной сети под решение конкретной задачи необходимо правильно задать оптимальное количество связей между нейронами, поскольку это значение будет определять характер выполняемого преобразования. Переобучения нейронной сети возможно избежать, следуя следующим правилам:

1) Количество нейронов во входном и выходном слоях задается по количество входных и выходных переменных в модели.

2) Количество нейронов в срытых слоях, а также количество срытых слоев задается так, чтобы количество образованных нейронами связей было в два раза меньше количества обучающих примеров в модели.

После определения начальной конфигурации нейронной сети происходит ее обучение. На текущий момент существует достаточное количество алгоритмов обучения нейронных сетей, которые детально реализованы, например, на языке программирования Python. Дальнейшие этапы работы с нейронной сетью зависят от поставленной задачи, выбранного алгоритма и среды, в который предполагается строить нейронные сети.

Определение зависимостей между показателями и создание системы линейных уравнений

Для успешного прогнозирования социально-экономических показателей на основе линейных регрессионных моделей эксперту-исследователю необходимо понимать исследуемую область, явления, объекты. Установка экономически-обоснованных связей между показателями позволяет делать правильные и практически применимые выводы по результатам эконометрических исследований. Отбор показателей для включения в уравнения также подкрепляется проведением корреляционного анализа. Однако даже при наличии высоких коэффициентов корреляции в первую очередь следует соотноситься с экономическим смыслом предполагаемых взаимосвязей показателей.

Для прогнозирования показателей по предпринимательству в Российской Федерации были отобраны 14 показателей и, соответственно, построено 14 уравнений, отражающих их зависимости между собой. Далее указанные факторы рассматриваются в контексте построенной модели показателей по предпринимательству.

В таблице 2 приведены полученные в результате исследования зависимости между показателями.

Таблица 2

Зависимости между показателями в модели

Для установленных зависимостей были построены матрицы корреляций. Средний модуль показателей корреляции зависимых переменных и объясняющих составил 0,7, что дополнительно подтверждает пригодность построенных уравнений зависимости для дальнейшего анализа в системе «Горизонт».

В рамках исследования были построены 14 регрессионных уравнений. Далее приводится пример расчета в системе «Горизонт» по одному из прогнозных показателей – выручка от продажи (SELL), рассчитываемого следующим образом:

SELL = 59689166600 – 250345700 IP1 - 106385300 TI1 – 352023300 CK1 + 0.317CUR,

где

· IP1 – Индекс потребительских цен;

· TI1 – Чистые налоги на производство и экспортно-импортные операции;

· CK1 – Расходы на конечное производство;

· CUR – Оборотные активы.

Прогноз осуществляется поквартально на весь 2022 год.

Затем проводится оценка качества построенной регрессионной модели. Все рассчитанные статистические характеристики построенной регрессионной модели приведены в Таблице 3.

Таблица 3

Статистические характеристика расчета показателя «выручка от продажи»

Аналогичным образом строятся регрессионные модели по всем выбранным показателям по предпринимательству.

Затем, чтобы оценить результаты прогнозирования показателей в целом по системе составляется матрица верификации результатов расчетов. Согласно авторской методологии краткосрочного и среднесрочного социально-экономического прогнозирования критериями качества регрессионной модели являются коэффициент детерминации R², критерий Дарбина-Уотсона DW, F-критерий Фишера. Критерием точности является ошибка MAPE (%). Для всех приведенных характеристик определены пороговые значения соответствующие низкому, среднему и высокому уровню качества и точности модели (таблицы 4, 5).

Таблица 4

Критерии качества моделей регрессии

Таблица 5

Критерий точности моделей регрессии

Все построенные регрессионные уравнения были оценены с помощью представленных критериев. Результаты приведены в Таблице 6.

Таблица 6

Характеристики построенных моделей

Оценка модели присваивается по наименьшему из критериев оценки. Таким образом, была составлена матрица верификации для всех построенных регрессионных уравнений (таблица 6).

Таблица 6

Матрица верификации уравнений регрессии

Исходя из матрицы верификации можно сделать вывод, что в системе показателей по предпринимательству есть уравнения регрессии, которые показали низкий уровень качества либо точности. Всего таких уравнений пять, и они относятся к расчету следующих показателей:

ODS – Оборотные активы денежные средства;

NONCURR – Внеоборотные активы;

PROF – Прибыль (убыток) до налогообложения;

AVTURN – Средний оборот дебиторской задолженности;

FOND – Фондоотдача (оборачиваемость основных средств.

Для улучшения прогнозов показателей, по которым регрессионные модели дают неудовлетворительные результаты, необходимо использовать интеллектуальные модели. В системе «Горизонт» уже реализована интеллектуальная модель нейронных сетей.

Прогнозирование на основе модели нейронных сетей

С помощью нейросетевого модуля были произведены расчеты для пяти показателям. Использование модуля нейронных сетей позволило незначительно улучшить расчетные значения критерия Дарбина-Уотсона. Кроме того, для показателя «прибыль (убыток) до налогообложения» (PROF) не удалось улучшить значение ошибки МАРЕ, которое согласно заданным пороговым значениям, осталось на низком уровне (таблицы 8, 9).

Таблица 8

Характеристики показателей для регрессионной модели

Таблица 9

Характеристики показателей для нейронной сети

Поскольку для большинства показателей применение нейронной сети не дало существенного улучшения в качестве и точности прогноза, было принято решение обратиться к другому методу интеллектуального анализа данных. На текущий момент в «Горизонт» реализован модуль деревьев решений. Развитием идеи дерева решений является модель случайного леса. Данная модель не была использована в системе «Горизонт», поэтому был разработан новый модуль случайного леса и встроен в гибридную систему «Горизонт».

Прогнозирование на основе модели случайного леса

В рамках исследования проводился поиск оптимальных значений параметров. Отправной точкой для начала поиска послужил параметр количество деревьев в ансамбле. Необходимо было найти такое количество деревьев в ансамбле, при котором достигалось бы наибольшее значение правильности (R²). Как правило, большее количество деревьев в ансамбле дает лучший результат. Это обусловлено тем, что усреднение результатов по большому числу деревьев позволит получить более устойчивый ансамбль за счет снижения переобучения. Поиск оптимальных значений параметров ансамбля деревьев производился с помощью метода перекрестной проверки.

С учетом небольшого количества предикторов и короткого временного ряда для перебора было выбрано десять различных значений количества деревьев – 5, 10, 15, 20, 25, 50, 100, 150, 200, 250. Увеличение количества деревьев в ансамбле слабо влияет на качество модели. Для расчетов было выбрано количество деревьев в ансамбле равным 200.

После определения количества деревьев в ансамбле рассчитывалось количество случайно отбираемых предикторов. Если значение этого показателя равно общему количеству предикторов в наборе данных, это означает, что в каждом разбиении данных могут участвовать все предикторы. Значение 1 означает, что при разбиении данных отбор вариантов расщеплений по разным предикторам не осуществляется. Оптимальное значение количества предикторов в нашем случае равно 2. Последним параметром, который учитывается при построении модели случайного леса, является глубина дерева. При увеличении глубины дерева снижается ошибка модели, однако максимальная глубина не всегда дает хорошее качество модели.

Итак, для построения прогноза по показателю «оборотные активы денежные средства» (ODS) была выбрана модель случайного леса с количеством деревьев 200, случайных предикторов 2 и глубиной 5. В результате расчетов удалось добиться увеличения качества модели (R²): с 83% и 79% на обучающей и контрольной выборке до 100% и 99%, соответственно.

Проведенные расчеты показали очень высокое качество построенной модели, что свидетельствует о ее практической применимости для прогнозирования показателя «оборотные активы денежные средства» (ODS).

Итоговые значения показателей качества и точности модели представлены в Таблице 10.

Таблица 10

Сравнение моделей регрессии и случайного леса для прогноза показателя ODS

В прогнозировании по модели случайного леса существенно повысилось значение критерия Дарбина-Уотсона, которое, согласно матрице верификации, соответствует высокому уровню качества.

Аналогичным образом с помощью модели случайного леса были спрогнозированы значения по всем показателям, для которых модель линейной регрессии показала неудовлетворительные результаты. Во всех случаях также удалось добиться повышения значений критериев качества и точности модели. Оценки качества и точности по лучшим построенным моделям приведены в таблице 11.

Таблица 11

Наилучшие значения качества и точности для всех моделей

Обновленная матрица верификации моделей представлена в таблице 12.

Таблица 12

Матрица верификации по лучшим моделям

Заключение

Таким образом, была построена гибридная модель прогнозирования показателей по предпринимательству, которая в результате сочетания моделей линейной регрессии и деревьев решений (случайного леса) позволила построить качественные прогнозы для всей совокупности показателей по предпринимательству в Российской Федерации.

Проведенные прогнозные расчеты показателей по предпринимательству основывались на прогнозных сценариях Банка России на 2021 год и период 2022 и 2023 годов [8].

Новые сценарии Банка России, опубликованные в ноябре 2022 г., на 2023 – 2025 годы разработаны с учетом нестабильности политической и экономической ситуации и дополнительно включают показатели платежного баланса [15]. В связи с подобными изменениями авторы планируют доработать системы уравнений для блоков макроэкономических показателей и показателей по предпринимательству с тем, чтобы проводить прогнозные расчеты в соответствии с актуальными сценариями.