Инновации в управлении городской инфраструктурой: экономико-математическая модель функционирования платных магистралей городских агломераций

Введение

В статье рассмотрены возможности формирования платных дорог и магистралей в крупных городах и агломерациях, а также системы сквозного управления движением на магистральных улицах крупных городов и городских агломераций.

Данная система должна обеспечивать эффективное взаимодействие светофорных систем (особенно светофорных систем городских магистралей и примыкающих к ним дорог, крупных развязок, а также мультимодальное взаимодействие в рамках городских транспортных систем (ГТС)).

Главное в функционировании подобных систем – наличие и постоянное обеспечение динамической обратной связи функционирования элементов системы и системы в целом с изменением параметров транспортного потока и времени суток.

Внедрение подобных систем представляет особый интерес в сочетании с идеей внедрения городских платных магистралей.

Городские скоростные автомагистрали в Японии и Австралии могут послужить примером внедрения подобных систем.

Однако для формирования подобного предложения необходимо изначально построить граф городской транспортной системы и провести анализ того, в какой степени внедрение подобных магистралей позволит решить проблему оптимизации транспортной доступности городских территорий.

Именно поэтому целью статьи является разработка новой экономико-математической модели функционирования платных магистралей в рамках городских агломераций.

Следует отметить, что проблема разработки экономико-математической модели функционирования платных магистралей остается незатронутой в современной исследовательской практике. Так, по запросу «платные магистрали» на портале ELIBRARY.RU можно обнаружить 5760 публикаций, однако за последние 5 лет по данной тематике имеется всего одна публикация [4] (Gavrilyuk, Shalagina, Dolenko, 2019).

Механизмы развития транспортной инфраструктуры нашли отражение в работах Аблязова Т.Х., Марусина А.В. [1] (Ablyazov, Marusin, 2019), Быковой О.Н., Пустохиной И.В. [3] (Bykova, Pustokhina, 2020), Квитко А., Карпова В., Петухова П., Ушакова А. [15] (Kvitko, Karpov, Petukhov, Ushakov, 2017), Керимова М., Сафиуллина Р. [14] (Kerimov, Safiullin, Marusin, Marusin, 2017) и др.

Концепции и модели транспортной логистики в условиях городских агломераций рассматриваются в научных статьях Андреева К.П. [2] (Andreev, 2017), Ковалевой Н.А., Мамаева Э.А. [6] (Kovaleva, Mamaev, 2015), Литвиненко Р.С., Павлова П.П., Аухадеева А.Э. [7] (Litvinenko, Pavlov, Aukhadeev, 2018), Макарова И.Н. [8] (Makarov, 2015), Олифир Д.И. [9] (Olifir, 2019), Перепелкина Н.А., Рыкалиной О.В., Тультаева Т.А. [10] (Perepelkin, Rykalina, Tultaev, 2019), Сагиновой О.В. [12] (Saginova, 2020), Ершовой С., Смирнова Е. [13] (Ershova, Smirnov, 2017), Завьялова Д.В. [5, 11] (Zavyalov, Pishchikova, Saginova, 2020; Saginov, Zavyalov, 2020) и др.

Также необходимо отметить, что к вопросу развития платных дорог мы уже неоднократно обращались, однако новые реалии требуют пересмотра и существенного уточнения имеющихся подходов. В частности, следует сказать, что обоснование модели городской транспортной магистрали с позиций экономико-математического научного подхода в современных российских научных публикациях не представлено.

Однако переход системы государственной власти к инструментарию программно-целевого управления требует в том числе объективных количественных способов обоснования государственных решений, необходимость которых применительно к вопросам развития городских транспортных систем мы и попытаемся обосновать в представленном исследовании.

При формировании модели выбора водителем частного автотранспортного средства следует учитывать, что этот выбор будет осуществляться исходя из следующих базисных вариантов:

1. Ехать по платной дороге.

2. Ехать по бесплатной дороге с пробками.

3. Воспользоваться общественным транспортом.

Однако необходимо учитывать, что в современном городе система платных дорог должна функционировать в сочетании с возможностью пересадки на общественный транспорт.

При этом линии городского общественного транспорта можно финансировать наряду с бюджетным финансированием за счет потока доходов от функционирования платных объектов инфраструктуры (дорог и парковок). Однако при этом необходимо, чтобы перехватывающие парковки были бесплатными, поскольку это, скорее всего, существенно повлияет на эффективность всей идеи «разгрузки» центров городов и основных магистралей за счет внедрения платных и бесплатных инфраструктурных объектов.

Рассмотрим ситуацию с нестабильной загруженностью городской транспортной инфраструктуры. Мы полагаем, что для теоретического анализа наибольший интерес будет представлять собой случай функционирования транспортной инфраструктуры города или городской агломерации на уровне, приближающемся к максимуму (максимальному использованию пропускной способности транспортных сетей города/агломерации), когда возникает конкуренция частного автотранспорта и транспорта предприятий за доступ к транспортной инфраструктуре и возможно формирование такой ситуации, что количество заявок в пиковые нагрузки будет превышать пропускную способность инфраструктуры (части инфраструктуры).

Рассматривая возможность формирования пиковых нагрузок в транспортных сетях крупных городов и агломераций, мы будем считать, что пики нагрузки могут быть циклические (суточные, недельные, месячные или сезонные) и нециклические, труднопредсказуемые, связанные, например, с малопредсказуемыми природными явлениями.

Рассмотрим, в первую очередь, самые простые модели, описывающие ситуацию конкуренции за транспортную сеть в межпиковый период времени. Среди таких моделей – теоретико-игровая модель доступа к автотранспортной инфраструктуре.

Рассмотрим ситуацию, когда на рынке существует некоторое ограниченное количество n игроков (автомобилей, находящихся в частном владении и принадлежащих крупным производственным предприятиям):

n N. (1)

Моделью транспортной сети будет служить некий граф G, который будет описывать моноцентрическую, паутинообразную или, гораздо реже, «решетчатую» сеть, которая чаще всего встречается в городах и городских агломерациях в нашей стране.

Однако в целях упрощения задачи фактически при неизвестной топологии сети можно представить конкуренцию игроков на графе как конкуренцию на сегменте.

Сформулируем условия задачи.

Пропускная способность транспортной инфраструктуры города/агломерации равно некой величине µ.

Количество игроков (отправителей и получателей грузов/товаров) равно n.

Поток заявок от каждого игрока (домохозяйства или производственного предприятия) можно условно принять равным количеству зарегистрированных автомобилей и автобусов:

λ_i = {λ_i, i = [1, n]}. (2)

Соответственно, общий поток заявок будет суммарным потоком заявок от совокупности игроков:

Λ = (3)

Таким образом, мы рассматриваем следующие ситуации:

А) Λ < µ;

Б) Λ ≈ µ;

В) Λ ≥ µ.

При этом данную задачу можно усложнить, введя пиковые значения, когда Λ > µ, и базовую ситуацию, когда поток заявок Λ = µ.

При рассмотрении функции общего транспортного потока в рамках любой территории, входящей в состав города или агломерации, необходимо также учитывать, что в нем будут принимать участие транспортные средства населения города, агломерации, региона и транзитный, главным образом грузовой, поток.

Таким образом, общий поток заявок можно представить:

Λ = = + + , (4)

где – совокупный транспортный поток (поток заявок), формируемый производственными и пассажирскими предприятиями города, агломерации;

– совокупный транспортный поток (поток заявок), формируемый транзитными перевозчиками;

– совокупный транспортный поток (поток заявок), формируемый транспортными средствами местных городских жителей.

Поскольку в большинстве крупных городов нашей страны в настоящее время существуют объездные автомобильные дороги, нагрузку на городскую транспортную систему от потока транзитных грузовых перевозчиков можно считать несущественной.

Представим, что в рамках города также существуют транспортные предприятия пассажирского транспорта, которые выступают в качестве некой коалиции, при этом действия частных лиц можно рассматривать как саморегулирующийся поток. Соответственно, фактически мы получаем ситуацию, когда несколько крупнейших игроков определяют траекторию развития элемента городской транспортной системы.

Для дальнейшего анализа следует сформулировать дерево состояний транспортной системы города.

Ситуация 1: Λ < µ.

Очевидно, что в данном случае ни муниципальные или региональные органы власти, ни частные лица, ни иные структуры не имеют существенной мотивации к вложению средств в транспортную инфраструктуру.

Ситуация 2: Λ ≈ µ.

Данную ситуацию можно рассмотреть как систему, состоящую из трех состояний:

1) дорога свободна в течение времени t_св: Λ < µ;

2) промежуточная ситуация, когда сеть меняет свое состояние от свободного к загруженному: Λ = µ. Данное состояние является неустойчивым:

t_пр << t_св + t_заг, (5)

где t_пр – время существования промежуточной ситуации;

t_св – время существования свободной дороги;

t_заг – время существования загруженной дороги;

3) имеет место формирование затора, характеризующегося временем существования Λ > µ.

Время существования одного цикла состояний транспортной сети:

t_пр + t_св + t_заг = t_{ц ,} (6)

где t_ц – время существования одного цикла состояний транспортной сети.

Фактически любое t_i можно представить в виде скалярного произведения времени t на вектор состояний системы , где каждое из состояний будет характеризоваться вероятностью х_i.

(7)

Ситуация 3: Λ > µ.

Очевидно, что в данном случае ветвь транспортной сети будет характеризоваться «затором» («пробкой»), которая будет носить постоянный хронический характер. В данном случае наиболее вероятно, что транзитные перевозчики предпочтут воспользоваться альтернативным маршрутом (при его наличии), а местные грузоотправители, перевозчики или региональные власти будут вынуждены принимать решение о модернизации транспортной сети.

Представим, что предприятия, выполняющие транспортное пассажирское обслуживание крупного города или городской агломерации, принадлежащие к коммерческому сектору перевозок, выступают в качестве некой коалиции, к которой не принадлежат муниципальные транспортные предприятия, осуществляющие пассажирские перевозки, при этом действия частных лиц и транзитных перевозчиков можно рассматривать как саморегулирующийся поток.

Внесем положение о том, что частный транспорт будет согласен оплачивать проезд при ожидании на альтернативной бесплатной дороге:

, (8)

где – время ожидания на альтернативной бесплатной дороге;

– время проезда по платной дороге легковым частным транспортом,

а для коммерческого пассажирского транспорта:

, (9)

где – время проезда по платной дороге пассажирским транспортом.

При этом предельное время ожидания коммерческих перевозчиков будет определяться соотношением выгод, потерь, спросом со стороны пассажиров, наполненностью салона и множеством других факторов. Фактически, проблема формально-математической постановки условия задачи о выборе водителем пассажирского транспортного средства (автобуса или «маршрутки») платного или бесплатного маршрута движения и ее общего решения уже сама является новой для отечественной транспортной науки, несет в себе элементы научной новизны и должна выступать в качестве темы отдельного исследования (диссертации).

В первом приближении, решение данной задачи может быть осуществлено эмпирическим путем.

Изначально будем считать, что в ситуации до реструктуризации транспортной сети у водителей нет выбора, и они вынуждены стоять в заторе, а в ситуации после реструктуризации транспортной сети городской агломерации или города и внедрения системы платных полос или платных магистралей они могут выбрать ехать по платной дороге или по бесплатной

При этом примем в качестве гипотезы, что пропускная способность бесплатной дороги не будет меняться после реконструкции/модернизации/строительства платной дороги:

µ_беспл ≤ µ , (10)

где µ_беспл – пропускная способность бесплатной магистрали.

Таким образом, элемент транспортной городской системы как система массового обслуживания из одноканальной с пропускной способностью µ становится двухканальной с пропускной способностью:

µ_рек = µ_беспл + µ_пл, (11)

где µ_рек – пропускная способность магистрали после реконструкции;

µ_пл – пропускная способность платной магистрали.

В данном случае также возможны следующие ситуации:

а) в качестве бесплатной остается старая дорога с пропускной способностью µ => µ ≡ µ_беспл;

б) в качестве бесплатной альтернативы будет предложена дорога пропускной способностью µ_беспл < µ с более низкокачественным дорожным покрытием и/или большей длиной маршрута и/или меньшей шириной проезжей части и/или большим количеством участков с затрудненным движением либо продолжительностью «пробок» {Δl_тр ≥ 0; Δt_тр ≥ 0; ΔЗ_тр ≥ 0}, где l_тр – абсолютное удлинение траектории движения; Δt_тр – абсолютное увеличение времени движения вследствие удлинения траектории движения.

Графически данные ситуации отображены на рисунке.

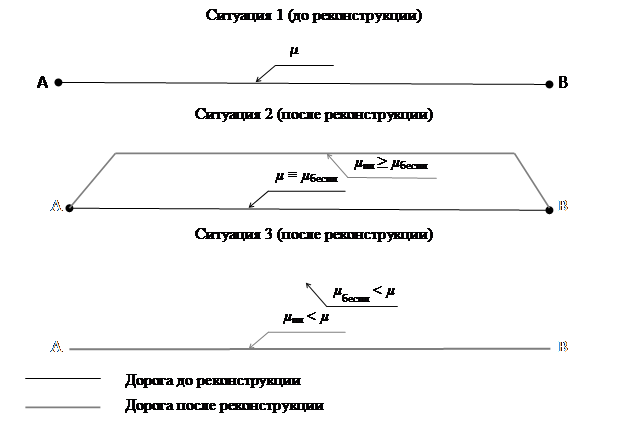
Рисунок. Графическое отображение вариантов реконструкции части автотранспортной сети как ребра графа

Источник: составлено авторами.

Также необходимо учитывать, что существует некая величина транспортных затрат, коррелирующая с потоком заявок и есть величина затрат на обновление инфраструктуры, которая также зависит от изменения совокупной пропускной способности:

З ~ Λ, (12)

З_инфр ~ Δµ, (13)

где З – некая величина затрат;

Λ – совокупная пропускная способность;

З_инфр – инфраструктурные затраты;

Δµ – изменение пропускной способности.

Соответственно, мы можем сформулировать постановку следующей задачи – нам необходимо разработать математическую модель и алгоритм принятия решения о возможности финансирования модернизации или строительства автотранспортной сети, либо платных участков транспортной сети города (городской агломерации) в зависимости от уровня использования пропускной способности. В данном случае среднее время обслуживания заявки будет равно отношению длины участка к средней скорости потока.

Рассмотрим ситуацию функционирования многоканальной системы массового обслуживания (далее – СМО) с ожиданием и ограничением на длину очереди.

В качестве каналов обслуживания в нашем случае могут выступать полосы движения: для магистрали с двусторонним движением это количество полос движения в каждом направлении.

Исходя из логических соображений, мы полагаем, что модель СМО с очередями будет применима к случаю до реструктуризации и к случаю после реструктуризации, когда будут существовать две дороги: бесплатная и платная.

Соответственно, согласно постулатам СМО, формула абсолютной пропускной способности магистрали как ветви графа будет выглядеть следующим образом:

(14)

где n – количество каналов обслуживания (полос магистрали, функционирующих в каждую сторону);

m – количество мест в очереди;

Ψ=λ/(nµ) – показатель нагрузки на один канал;

Q – относительная пропускная способность;

– условный показатель, характеризующий пропускную способность:

. (15)

Очевидно, что в таком случае фактическая вероятность отказа будет равна λ/µ, а в случае с многоканальной СМО фактическая вероятность отказа составит:

(16)

где ϑ – фактическая вероятность отказа в многоканальной СМО;

R – количество ребер графа, задействованных в СМО;

(17)

где – условный показатель

Также можно принять в качестве теоретической модели функционирования автотранспортной системы города (городской агломерации) модель СМО с ожиданием и неограниченной очередью. Как отмечается в большинстве исследований, посвященных СМО с ожиданием и неограниченной очередью, в данном случае предельный (стационарный) режим марковского случайного процесса, протекающего в СМО, будет существовать при условии, что интенсивность обслуживания всех n каналов будет выше интенсивности λ входящего потока.

При стационарном λ ≥ µn потоке необходимо сделать вывод о том, что очередь в системе будет нарастать без ограничений, поэтому в конечном итоге система не сможет осуществлять свое функционирование вследствие закупорки каналов системы.

Вместе с тем, учитывая, что имеет место суточное варьирование потока, мы можем оценить примерные величины, при которых данная система еще будет функционировать.

Исходя из формулы для определения среднего числа заявок в многоканальной СМО:

(18)

где – среднее число заявок в многоканальной СМО.

При этом предполагая, что в суточном цикле

λ_max ≡ µ, (19)

мы получим следующую систему

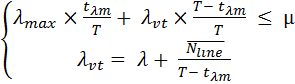. (20)

При этом необходимо учитывать, что время Т фактически является временем суточного цикла траффика (24 часа). Для получения формального решения задачи о суточном траффике необходимо оценить соотношение между λ_max и λ в суточном траффике.

Однако очевидно, что для возможности функционирования системы должно соблюдаться соотношение:

λ_max ≥ λ. (21)

При несоблюдении ряда указанных условий принятие решения о реконструкции сети будет необходимо для реализации возможности физического обеспечения транспортным обслуживанием территорий города (агломерации).

При этом мы имеем следующие теоретически возможные варианты финансирования модернизации сети:

1. Отсутствие финансирования.

2. Частное финансирование за счет крупных предприятий города и основных коммерческих перевозчиков сферы пассажирского транспорта.

3. Частное финансирование за счет крупных предприятий города, основных коммерческих перевозчиков сферы пассажирского транспорта, транзитного потока, потока частных легковых транспортных средств.

4. Государственное финансирование за счет федеральных и/или региональных органов власти.

5. Смешанные варианты государственно-частного финансирования.

В контексте игры у каждого крупного предприятия, включая коммерческих перевозчиков, в данном случае возможны две стратегии – вкладывать деньги в реконструкцию транспортной сети или не вкладывать.

При этом в рамках самой игры возможны следующие варианты поведения участников:

1. Варианты поведения государства:

- вкладывать бюджетные деньги в модернизацию сети;

- сформировать партнерство с крупными производителями региона;

- привлечь стороннего оператора;

- остаться в стороне от проблемы.

2. Варианты поведения частного партнера:

- участвовать в проекте с оплатой за счет государства;

- участвовать в проекте с оплатой за счет производственных фирм;

- участвовать в проекте с финансированием за счет консолидации распределенных частных средств (транзитного грузопотока и автотранспортных средств местного населения);

- участвовать в проекте с финансированием за счет собственных средств.

Вероятность получения финансовых средств от транзитного потока на платном участке пути существенно зависит от длины очереди на альтернативном маршруте. При этом для «маршрутчиков» (коммерческих перевозчиков) мы примем в качестве методологической базы модель рационального человека и, как следствие, будем считать, что выбор маршрута будет рациональным исходя из соотношения затрат, сопутствующих различным вариантам выбора. В свою очередь, для частных лиц в качестве основных факторов, оказывающих наиболее существенное влияние на принятие решения, мы выделим необходимость экономии времени, или уровень терпимости к очереди, и склонность к сбережению средств.

Формализуем данные размышления и рассмотрим все отмеченное в категориях затрат и выигрышей.

Необходимо определить, в каком случае владелец частного автомобиля воспользуется платной дорогой. В качестве базовой модели поведения водителя мы позиционируем модель рационального экономического человека и, соответственно, рационального выбора.

В данном случае будем исходить из затратного подхода, считая, что основой рационального выбора выступают совокупные затраты.

Совокупные затраты частного лица при движении по дороге в собственном автомобиле, при рассмотрении наиболее типичной ситуации, по всей видимости, будут складываться из следующего перечня затрат:

1. Прямые затраты на преодоление более длинного участка пути:

Зп1 = Δl_тр * Ц_топл * У_рт, (22)

где Ц_топл – цена единицы топлива;

У_рт – удельный расход топлива.

2. Изменения удельного потребления топлива при движении по дороге с менее качественным покрытием:

Зп2 = Δl_тр * Ц_топл * ΔУ_рт. (23)

3. Изменение вероятности отказа деталей автомобилей (поломки) при движении по менее качественному покрытию:

Зп3 = Δl_тр * Ц_рем * ΔУ , (24)

где Ц_рем – стоимость ремонта в случае отказа;

У – удельная вероятность отказа.

Здесь необходимо оговориться, что удельная вероятность отказа оценивается, как правило, водителем исключительно интуитивно. Тем не менее может оказаться полезным разработка и введение категорий диапазонов качества покрытия, коррелирующих с возможными диапазонами отказа деталей автомобилей.

4. Изменение затрат времени при движении по менее качественному покрытию, либо по более длинному маршруту, либо по маршруту, характеризующемуся большей продолжительностью заторов или их большей протяженностью. В данном случае принципиальное значение имеет субъективная и объективная оценка водителем стоимостных затрат своего времени, а также объективная стоимость единицы времени водителя или пассажира. Упрощенно посчитать данный показатель возможно следующим образом:

Ц_т = , (25)

где Ц_т – стоимость единицы времени труда водителя.

Соответственно, потери от удлинения времени в пути будут:

Зп4 = ΔТ_п × Ц_т, (26)

где ΔТ_п – изменение времени в пути по сравнению с кратчайшим и комфортным путем.

5. Критерий комфорта движения. Данный критерий потенциально также может оцениваться в денежном выражении. Его можно оценить как трудозатраты – энергозатраты на управление транспортным средством.

Соответственно, сопоставив величину энергозатрат водителя на управление транспортным средством на километр пути по старой автомобильной дороге и дороге после реконструкции, можно оценить комфортность пути.

Можно высчитать единицу стоимости энергозатрат водителя (Ц_эз) как:

Ц_эз = . (27)

Соответственно,

Зп5 = , (28)

где ΔЭЗ – среднее изменение энергозатрат водителя на управление автомобилем по менее качественной дороге.

Исходя из концепции рационального выбора, мы можем сформулировать максимальный верхний предел цены (Ц_max), по которой водитель будет согласен проехать по платной автодороге:

Ц_max ≤ Зп1 + Зп2 + Зп3 + Зп4 + Зп5. (29)

Если рассматривать ситуацию с точки зрения владельца (фирмы-оператора) инфраструктуры, то минимальной ценой за проезд может быть следующая цена (Ц_мин):

Ц_мин (30)

где СЗ_{стр,экс} – совокупные затраты на строительство и эксплуатацию за

период жизненного цикла.

Идеальным вариантом будет совпадение данных цен, либо цена с позиции собственника должна быть не более цены с позиции владельца автомобиля.

Теперь перейдем к следующему вопросу нашего исследования. В каком случае частные производители либо перевозчики смогут финансировать строительство и эксплуатацию инфраструктуры в городе (агломерации)?

Очевидно, что в этом случае в функцию транспортных затрат производителя или частного перевозчика войдут затраты собственника автомобиля (автобуса) и затраты, связанные с задержками в доставке груза или с недостаточным спросом со стороны пассажиров (неполным заполнением салона пассажирского транспортного средства).

В результате всего вышеприведенного мы можем сформулировать постановку управленческой задачи, которую необходимо будет решить в каждом конкретном случае при формировании вопроса об оптимальной цене за пользование платной составляющей городской транспортной инфраструктуры: оценить вариативность составляющих транспортного потока и вычислить вероятность образования очереди и возможную длину очереди уже в каждой конкретной ситуации на основе реальных параметров сети и транспортного потока территории. На основе этих вычислений, в свою очередь, требуется разработать схему принятия решения о модернизации/реструктуризации транспортной сети города с формированием платных магистралей либо с выделением платных полос на существующих городских магистралях.

В случае участия в проблеме крупных производственных предприятий и предприятий, занимающихся пассажирскими перевозками на коммерческой основе, наиболее существенной проблемой, скорее всего, будет вопрос о долях оплаты и участии каждого из предприятий в реконструкции сети, то есть основным вопросом будет вопрос «безбилетника». Решение этого вопроса, в первую очередь, будет зависеть от политической воли муниципальной или региональной власти.

Необходимо будет также формально и финансово определить зону ответственности государства в лице органов власти и муниципалитетов для формирования цены проезда, не превышающей оптимальных значений, и недопущения злоупотреблений со стороны компании-оператора.

Рассматривая данную ситуацию в контексте мирового опыта (прежде всего Германии и Латинской Америки), представляется, что инициатором модернизации транспортной инфраструктуры в регионе, вероятнее всего, выступит то из промышленных или пассажирских транспортных предприятий, траффик которого составляет наибольшую долю в общем траффике сети. В соответствии с концепцией справедливой цены в этом случае затраты на модернизацию транспортной инфраструктуры должны лечь на принимающие участие в проекте частные промышленные и транспортные организации и частных лиц пропорционально долям траффика.

Соответственно, мы получим следующие соотношения:

Д_опчт = , (31)

где Д_опчт – общая предполагаемая величина дохода от частного траффика;

ПЭЗ_{стр,экс} – приведенные к году эксплуатации затраты на строительство и эксплуатацию платной дороги;

СД_чт – совокупная доля в общем городском траффике от частного траффика промышленных и транспортных предприятий;

ЦП_уа = , (32)

где ЦП_уа – цена проезда условного автомобиля;

ВТ – величина трафика.

В дальнейшем должна определяться стоимость проезда каждой категории транспортных средств в зависимости от их доли в общей величине траффика транспортной системы крупного города или агломерации.

Заключение

Таким образом, нами сформулирована экономико-математическая модель, которая может быть использована для формирования оптимальной цены проезда по платной городской автодороге, и получены теоретические подходы к формированию методики решения данной задачи в общем виде.

Направления дальнейших исследований могут быть связаны с апробацией экономико-математической модели формирования оптимальной цены проезда по платной городской автодороге на практике.