Показатели чувствительности к процентному риску
Скачать PDF | Загрузок: 30
Статья в журнале
Российское предпринимательство *
№ 9 (57), Сентябрь 2004
* Этот журнал не выпускается в Первом экономическом издательстве
Аннотация:
Продолжение. Начало в №№ 11, 12/2003, 4, 5, 6, 7/2004. Напомним, что в предшествующих публикациях нами подчеркивался факт того, что процентный риск субъектов рынка всегда связан с возможными потерями, вызываемыми непредсказуемым изменением рыночных процентных ставок. Дело в том, что курсовая стоимость долговых финансовых инструментов (например, облигаций) определяется требуемой рынком доходностью. Так, например, для равновесного рынка справедливая стоимость купонной облигации может быть оценена в соответствии с выражением (1).
Ключевые слова: рынок, факторы риска, оценка риска, долговые инструменты
Продолжение. Начало в №№ 11, 12/2003, 4, 5, 6, 7/2004
Напомним, что в предшествующих публикациях нами подчеркивался факт того, что процентный риск субъектов рынка всегда связан с возможными потерями, вызываемыми непредсказуемым изменением рыночных процентных ставок. Дело в том, что курсовая стоимость долговых финансовых инструментов (например, облигаций) определяется требуемой рынком доходностью. Так, например, для равновесного рынка справедливая стоимость купонной облигации может быть оценена в соответствии с выражением (1).
![]() , (1)
, (1)
где ![]() – текущая рыночная цена облигации (справедливая стоимость);
– текущая рыночная цена облигации (справедливая стоимость);
![]() – количество лет до погашения облигации;
– количество лет до погашения облигации;
![]() – требуемая рынком доходность облигации к погашению (рыночная процентная ставка);
– требуемая рынком доходность облигации к погашению (рыночная процентная ставка);
![]() – денежный поток, доступный инвесторам в период времени
– денежный поток, доступный инвесторам в период времени![]() (в год
(в год![]() ). В частности, в качестве денежных потоков могут быть ежегодные купонные платежи и выплата номинальной стоимости облигации при её погашении.
). В частности, в качестве денежных потоков могут быть ежегодные купонные платежи и выплата номинальной стоимости облигации при её погашении.
Графически зависимость ![]() от
от ![]() имеет вид, представленный на рис. 1.
имеет вид, представленный на рис. 1.
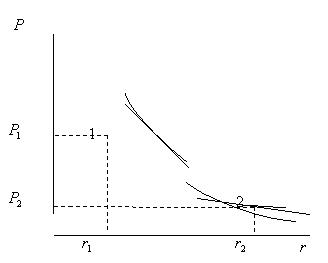
Рис. 1. Зависимость стоимости долгового инструмента от величины рыночных процентных ставок.
Анализ рис. 1 показывает, что при возрастании рыночных процентных ставок (например, с некоторого значения ![]() до значения
до значения![]() ) стоимость долгового финансового инструмента для обеспечения требуемой рынком доходности должна уменьшиться (со значения
) стоимость долгового финансового инструмента для обеспечения требуемой рынком доходности должна уменьшиться (со значения ![]() до значения
до значения ![]() ). При этом рынок рассматриваемых облигаций переходит из состояния 1 в состояние 2 (см. рис. 1). При уменьшении рыночных процентных ставок наблюдается обратная картина: цена облигации возрастает. Кроме того, из-за нелинейности рассматриваемой зависимости чувствительность
). При этом рынок рассматриваемых облигаций переходит из состояния 1 в состояние 2 (см. рис. 1). При уменьшении рыночных процентных ставок наблюдается обратная картина: цена облигации возрастает. Кроме того, из-за нелинейности рассматриваемой зависимости чувствительность ![]() к изменениям
к изменениям ![]() не остается постоянной величиной. Так, например, в окрестностях точек 1 и 2 при одинаковых отклонениях
не остается постоянной величиной. Так, например, в окрестностях точек 1 и 2 при одинаковых отклонениях ![]() относительно своих исходных уровней (
относительно своих исходных уровней (![]() и
и ![]() ) цена облигации будет изменяться по-разному. В точке 1 изменения будут более значительными. Об этом свидетельствует различный наклон касательных, проведённых к указанным точкам на кривой (см. рис. 1).
) цена облигации будет изменяться по-разному. В точке 1 изменения будут более значительными. Об этом свидетельствует различный наклон касательных, проведённых к указанным точкам на кривой (см. рис. 1).
Таким образом, инвестор в долговые инструменты может понести убытки при увеличении процентной ставки, так как стоимость его активов уменьшается. Эмитент долговых инструментов (например, облигаций) также подвержен процентному риску. При увеличении процентных ставок возрастают издержки на финансирование организации. С целью эффективного управления процентным риском необходимо осуществлять количественную оценку чувствительности стоимости долговых инструментов к изменениям рыночной процентной ставки. То есть, необходимо установить зависимость ![]() от
от ![]() . Для решения этой задачи при малых отклонениях
. Для решения этой задачи при малых отклонениях ![]() можно воспользоваться двумя первыми членами формулы Тейлора:
можно воспользоваться двумя первыми членами формулы Тейлора:
![]() , (2)
, (2)
где первая и вторая частные производные ![]() и
и ![]() являются коэффициентами, характеризующими чувствительность
являются коэффициентами, характеризующими чувствительность ![]() к изменениям
к изменениям ![]() .
.
В тех случаях, когда![]() не превышает 1% от исходного значения процентной ставки, хорошую точность при прогнозировании
не превышает 1% от исходного значения процентной ставки, хорошую точность при прогнозировании ![]() может обеспечить одно первое слагаемое выражения (2). Это существенно упрощает вычисления. Если же изменения процентной ставки более значительны, то для уменьшения погрешности прогнозирования
может обеспечить одно первое слагаемое выражения (2). Это существенно упрощает вычисления. Если же изменения процентной ставки более значительны, то для уменьшения погрешности прогнозирования ![]() необходимо вычислять и второе слагаемое в (2).
необходимо вычислять и второе слагаемое в (2).
Наряду с аналитическим выражением рассматриваемой зависимости часто используют её графическое изображение (графика риска) [2]. На рис. 2 представлен график риска в точке 1 на кривой «![]() от
от ![]() » (см. рис. 1) с исходными параметрами
» (см. рис. 1) с исходными параметрами ![]() . Для построения этого графика требуется провести ось абсцисс через указанную точку (то есть уменьшить на величину
. Для построения этого графика требуется провести ось абсцисс через указанную точку (то есть уменьшить на величину ![]() все значения исходной функции). В результате такого переноса наклон касательной к точке 1 не меняется.
все значения исходной функции). В результате такого переноса наклон касательной к точке 1 не меняется.
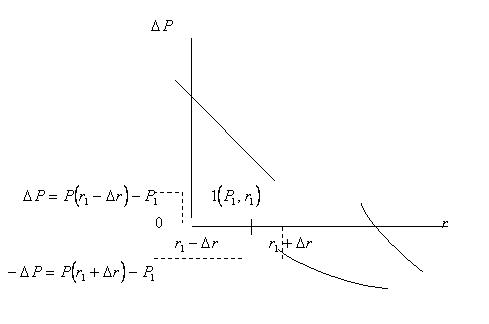
Рис. 2. График риска
Таким образом, для оценки чувствительности к процентному риску необходимо вычислить значения частных производных ![]() и
и ![]() .
.
На основании (1)
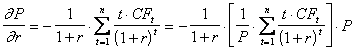 . (3)
. (3)
Выражение в квадратных скобках в формуле (3) представляет собой средневзвешенный срок до погашения долгового финансового инструмента и называется дюрацией (duration – D). В качестве весовых коэффициентов при вычислении дюрации используются отношения приведённых стоимостей платежей соответствующих периодов к суммарной приведённой стоимости всех платежей по данному долговому инструменту. То есть,
![]() ,
,
где 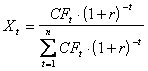 ;
; ![]() .
.
Впервые понятие дюрации было введено в 1938 году английским экономистом Фредериком Маколеем. С тех пор это понятие широко используется в финансовом анализе. В частности, величину дюрации часто трактуют, как средний срок возврата капитала для инвестора, вкладывающего денежные средства в долговые инструменты и сохраняющего их до погашения. Для эмитента значение дюрации трактуют как средний период владения капиталом, привлечённым путём размещения соответствующих долговых обязательств [1].
Таким образом, выражение (3) с учётом дюрации может быть переписано в следующем виде:
![]() , (4)
, (4)
где ![]() – модифицированная дюрация.
– модифицированная дюрация.
На основании (2) и (4) можно записать выражения для абсолютного и относительного изменения стоимости долгового инструмента.
![]() , (5)
, (5)
![]() . (6)
. (6)
Таким образом, при малых значениях ![]() (менее 1% относительно исходного значения)
(менее 1% относительно исходного значения)![]() достаточно полно характеризует чувствительность стоимости долгового инструмента к изменению процентных ставок (наклон графика риска, см. рис. 2). Чем больше
достаточно полно характеризует чувствительность стоимости долгового инструмента к изменению процентных ставок (наклон графика риска, см. рис. 2). Чем больше ![]() , тем больше эта чувствительность (и тем большая подверженность процентному риску). Поэтому для купонных облигаций при прочих равных условиях [3]:
, тем больше эта чувствительность (и тем большая подверженность процентному риску). Поэтому для купонных облигаций при прочих равных условиях [3]:
‑ чем больше срок до погашения, тем больше ![]() и тем большая чувствительность к изменению рыночных процентных ставок;
и тем большая чувствительность к изменению рыночных процентных ставок;
‑ чем меньше размер купонных выплат, тем больше ![]() и тем большая чувствительность к изменению рыночных процентных ставок. Для бескупонных облигаций дюрация Маколея равна сроку до погашения;
и тем большая чувствительность к изменению рыночных процентных ставок. Для бескупонных облигаций дюрация Маколея равна сроку до погашения;
‑ чем ниже исходный уровень рыночных процентных ставок, тем больше ![]() и тем большая подверженность процентному риску.
и тем большая подверженность процентному риску.
Можно также вычислить модифицированную дюрацию портфеля долговых финансовых инструментов (![]() ) и использовать её для оценки чувствительности этого портфеля к изменению рыночной процентной ставки. При этом,
) и использовать её для оценки чувствительности этого портфеля к изменению рыночной процентной ставки. При этом, ![]() представляет собой взвешенную по стоимости сумму модифицированных дюраций долговых инструментов, входящих в данный портфель. То есть:
представляет собой взвешенную по стоимости сумму модифицированных дюраций долговых инструментов, входящих в данный портфель. То есть:
![]() ,
,
где ![]() модифицированная дюрация i-го долгового инструмента; i = 1,2, …, m;
модифицированная дюрация i-го долгового инструмента; i = 1,2, …, m;
![]() весовой коэффициент – отношение рыночной стоимости i-го долгового инструмента к рыночной стоимости всего портфеля;
весовой коэффициент – отношение рыночной стоимости i-го долгового инструмента к рыночной стоимости всего портфеля; ![]() ;
;
![]() количество долговых инструментов в портфеле.
количество долговых инструментов в портфеле.
Выражения, аналогичные (5) и (6), для портфеля долговых финансовых инструментов будут иметь следующий вид:
![]() ,
,
![]() ,
,
где ![]() рыночная стоимость портфеля долговых инструментов;
рыночная стоимость портфеля долговых инструментов;
![]() абсолютное изменение рыночной стоимости портфеля долговых инструментов.
абсолютное изменение рыночной стоимости портфеля долговых инструментов.
Являясь линейной аппроксимацией графика риска (см. рис. 2), дюрация не даёт хороших результатов при значительных (больших 1% относительно исходного уровня) изменениях рыночной процентной ставки. В этом случае, наряду с дюрацией, необходимо рассчитывать и другие показатели чувствительности. В соответствии с (2) таким показателем является вторая частная производная ![]() , которая называется выпуклостью.
, которая называется выпуклостью.
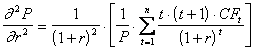 .
.
Таким образом, основными показателями чувствительности долговых финансовых инструментов к изменению рыночной процентной ставки являются дюрация и выпуклость. Совместное их использование даёт возможность достаточно точно оценивать подверженность субъектов рынка процентному риску.
Продолжение следует
Источники:
2. Маршалл Дж.Ф., Бансал В.К. Финансовая инженерия: Полное руководство по финансовым нововведениям / Пер. с англ. – М.: ИНФРА-М, 1998. – 784 с.
3. Фабоцци Ф. Управление инвестициями / Пер. с англ. – М.: ИНФРА-М, 2000. – 932 с.
Страница обновлена: 16.12.2025 в 06:55:27
Download PDF | Downloads: 30
Pokazateli chuvstvitelnosti k protsentnomu risku
Selyukov V.K.Journal paper
