Сравнительный анализ теории нечетких множеств и классического вероятностного подхода к оценке возможности неблагоприятного исхода венчурных инвестиций

Выбор метода оценки риска должен зависеть от точности получаемых оценок, сложности проводимых вычислений, интуитивного понимания алгоритма расчетов и прочих факторов, обеспечивающих удобство в практическом применении метода. Так, во многих работах утверждается, что нечетко-множественный инструментарий во многих случаях проще вероятностных методов. Даже исследователи, утверждающие родственность двух подходов, указывают, что теория нечетких множеств может быть более доступна для практического использования.

Таким образом, нам предстоит рассмотреть вероятностный подход к анализу риска и на его основе рассчитать числовые характеристики рискованности проекта. Полученные результаты будут проанализированы с целью сравнения двух альтернативных подходов. В итоге, нижеследующее исследование должно дать ответ на следующие вопросы:

влияет ли выбор инструментария, используемого для построения модели неопределенности факторов, на результаты исследования?

какой из рассматриваемых методов предпочтительнее, исходя из точности оценок, сложности вычислений и их интуитивного понимания, доступности компьютерных приложений для анализа?

Рассмотрим алгоритм оценки риска, используемый вероятностным подходом. На начальном этапе необходимо построить модель неопределенности каждого фактора риска. Затем на их основе определить модель неопределенности для показателей эффективности, после чего рассчитать интегральную оценку рискованности проекта, как возможности неблагоприятного исхода. Несколько другими будут лишь способы реализации данных процедур.

Для задания неопределенности фактора риска X необходимо описать функцию распределения F(x) или плотность распределения f(x). Последняя будет иметь тот же профиль, что и функция принадлежности для каждого конкретного фактора. В непрерывном случае снимается ограничение на максимальное значение характеристической функции (в данном контексте - функции плотности): теперь она не ограничена сверху единицей. Однако появляется новое условие, вызванное спецификой вероятностного подхода:

. (1)

Если неопределенность моделируется на основе ранжирования различных значений рискового фактора, это не будет иметь особого значения. Условие 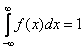лишь изменит масштаб значений характеристической функции, полученной по итогам опроса. Если же эксперта просят задать точечные характеристики возможности различных значений, то спрашиваемому субъекту, очевидно, будет труднее определить вероятность, чем принадлежность. Однако точечные оценки экспертов редко используются на практике по причине низкой их достоверности. Потому указанную разницу в ограничениях будем считать несущественной.

Построим функцию плотности распределения, которая будет иметь форму треугольника. Его основание ограничено интервалом будущих значений фактора. Максимум функции достигается в точке наиболее возможного значения и равен высоте треугольника, определяемой из условия

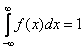. (2)

Описанный подход, предполагающий проведение расчетов с треугольными и трапезоидными случайными числами, получаемыми на основе экспертных оценок, достаточно распространен в теоретических исследованиях, касающихся анализа рисков. [1, 2].

Описав таким образом неопределенность факторов риска, необходимо многократно провести имитацию реализации проекта. На каждой итерации переменные проекта принимают значения соответственно заданным законам распределения и порождают результат, который при определенных допущениях можно полагать случайным. В итоге, получим совокупность значений критериев эффективности, по которой можно построить закон распределения вероятностей для каждого из них. Проведем соответствующие вычисления для инвестиционного проекта. Построив треугольные вероятностные модели неопределенности валютных курсов и осуществив 1000 имитаций реализации проекта, получим следующие гистограммы частот показателей эффективности (рис. 1).

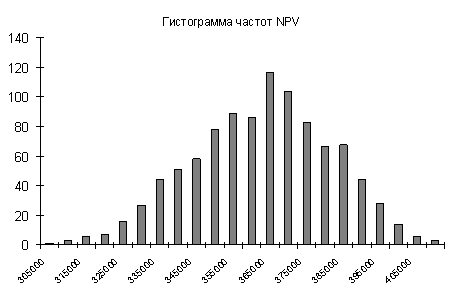
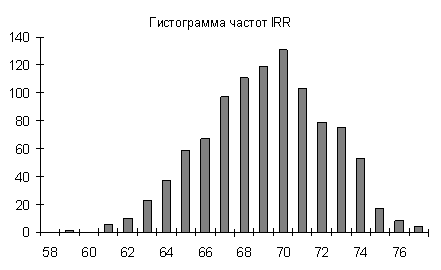
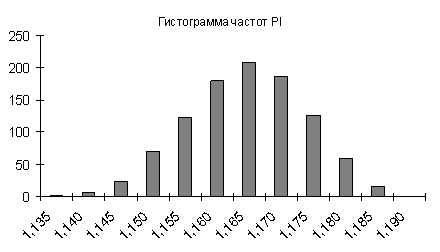
Рис. 1. Вероятностные модели неопределенности показателей эффективности

Форма распределения вероятностей критериев эффективности аналогична тому, что мы можем получить при использовании теории нечетких множеств. Здесь также прослеживаются черты треугольного распределения. Близки и граничные значения критериев эффективности.

Далее необходимо рассчитать интегральную оценку риска. Заметим, что проблема количественной оценки рискованности, получаемой при агрегировании неопределенных результатов, сравнительно больше проработана для вероятностного подхода, предоставляющего аналитику целый спектр различных показателей. Для корректности сравнения среди них необходимо выбрать критерий, наиболее соответствующий V&M. В качестве такого показателя логично использовать вероятность неэффективности проекта [3]. Так, если критерием эффективности является NPV, то данная величина составит:

, (3)

где f(NPV) – функция плотности распределения данного показателя. Значения вероятности неэффективности проекта, рассчитанные для полученной выборки, представлены в табл. 1.

Таблица 1

Сравнение оценок риска, рассчитанных по различным подходам

Критическое значение NPV	350000	P_NPV	0,26	V&M_NPV	0,24
Критическое значение IRR	60	P_IRR	0,01	V&M_IRR	0,01
Критическое значение PBP	10	P_PBP	0	V&M_PBP	0
Критическое значение PI	1	P_PI	0	V&M_PI	0

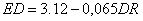Задание функциональной зависимости между факторами риска в следующей форме так же, как и ранее приводит к улучшению проектных характеристик. Проект по-прежнему окупается на тринадцатый месяц с начала реализации. Параметры характеристических функций (гистограмм) соответствуют функциям принадлежности, полученным в рамках нечеткого подхода.

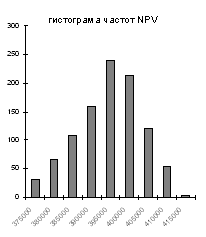
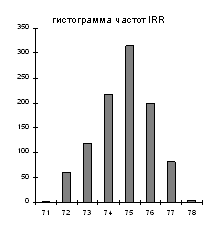
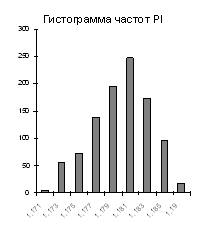
Рис. 2. Вероятностные модели неопределенности показателей эффективности в случае зависимости факторов риска

Результаты сравнительного анализа двух подходов представлены в табл. 2.

Таблица 2

Результаты сравнительного анализа подходов

Критерий	Результат сравнения
Распространенность	Нечеткий подход менее распространен на практике (новизна)
Доступность	Вероятностный подход реализован практически во всех приложениях. Напротив, существует сравнительно небольшое число прикладных пакетов, поддерживающих операции над нечеткими числами. В то же время, вычисления с нечеткими числами легко реализовать, например, в виде макросов для MS Excel.
Сложность	Вычисления, предполагаемые анализируемыми подходами, характеризуются одинаковой степенью сложности вычислений.
Риски	Вероятностный и нечеткий подходы дают схожие оценки рискованности проекта
Точность	Сравниваемые подходы в равной степени зависят от вида распределения факторов риска и характеризуются примерно одинаковой степенью точности.

Полученные результаты свидетельствуют о том, что рассматриваемые подходы дают схожие оценки рисков проекта.