Развитие модели Арнольда как инструмента анализа экономической безопасности социально-экономических систем

Введение. Сегодня вопросы управления рисками занимают центральное место в формировании стратегий социально-экономических систем. Особенно активно эти вопросы стали разрабатываться в конце 1999-х-начале 2000 гг. Понятия риска и неопределенности рассмотрены Ф. Найтом в работе 1994 г. [13]. Содержательное определение термина «риск» дано, например, в 1997 г. И.В. Бернаром и Ж.К. Колли [6].

В это время вопросы управления рисками приобрели особенную важность для России. Так, М.А. Эскиндаров отмечает в 1999 г. «… сейчас Россия переживает становление очередной системы хозяйствования, которой предстоит функционировать значительный отрезок времени. Одновременно создаются присущие ей организационно-хозяйственные формы (экономические институты), определяющие новые «правила игры», призванные внести определенный порядок в систему взаимоотношений рыночных субъектов, в повседневную хозяйственную жизнь … возникающие хозяйственные структуры появляются с нарушением формальных правил, сложившейся нормативно-правовой базы, что, несомненно, будет вести к конфликтам и обеспечивать противоречивое развитие, складывающихся систем и форм хозяйствования…» [17].

В 2010-х г. происходило развитие теории системного управления рисками [1, c. 240-251; 2; 4, с. 502]. Исследовались вопросы обеспечения экономической безопасности [10, с. 202; 11, с. 73]. Активно развивались инструменты практического применения теории управления рисками [7; 12; 14-16].

В то же время, некоторые аспекты управления рисками, как основы экономической безопасности исследованы недостаточно. В настоящей статье рассматривается задача использования аппарата линейных дифференциальных уравнений для исследования устойчивости производственной системы, в качестве примера которой выступает типовое предприятие лесопромышленного комплекса. Данное предприятие выполняет работы по собственным лесозаготовкам и приобретению лесоматериалов у мелких лесозаготовителей, транспортировке лесоматериалов на нижний складской комплекс, с последующими поставками на заводы для дальнейшей переработки.

Риском для рассматриваемой компании, требующим регулирования, является возможность срыва поставок на заводы и нарушение соответствующих договорных обязательств с одной стороны, и затоваривание складов, с другой стороны. В настоящей работе данный риск может регулироваться путем коррекции потока поставок на склад и отгрузок продукции при росте рассогласования между требуемым объемом продукции на складах и ее фактическим наличием.

Однако при таком подходе к управлению генерируется другой риск – риск потери устойчивости управления. При сосредоточии прав на верхнем уровне иерархии – управление приводит к риску потери устойчивости системы, если уровней управления более двух. Практически, устойчивость обеспечивается только при организации управления таким образом, что все исполнители подчиняются одному руководителю. Однако такое построение управления возможно только в небольших компаниях из-за ограничения управляемости.

По словам В.И. Арнольда [3] «Эти выводы, сделанные … на основании анализа простейшей жесткой модели, на самом деле выдерживают проверку на структурную устойчивость, исключая лишь случай n = 2: двухступенчатое управление может оказаться как устойчивым, так и неустойчивым, в зависимости от деталей организации дела, которыми мы … пренебрегли при составлении нашей самой простой модели … Длительное и, по-видимому, устойчивое функционирование системы многоступенчатого управления в СССР объяснялось, вероятно, неисполнением директивных указаний и существованием «теневой» системы заинтересовывания управляющих различных рангов в интересах дела.

Без такой реальной заинтересованности (которая в современных условиях уже не обязательно обеспечивается коррупцией) многоступенчатое управление всегда ведет к разрухе…».

Способом воздействия на риск потери устойчивости является передача прав по управлению на нижние уровни иерархии. Однако повышение самостоятельности управляющих нижних уровней иерархического управления повышает риск злоупотреблений в компании.

Ниже рассмотрен вопрос построения модели управления компанией лесопромышленного комплекса, основанной на использовании обратных связей, и исследовании на основе анализа дифференциальных уравнений этой модели с целью минимизации риска злоупотреблений при обеспечении устойчивости управления компанией.

Основная часть. Используем параметрический векторный функциональный граф [9] для визуального представления связей компании. Рассмотрим два представления. В первом случае вершины графа – это организационные подсистемы компании. Изображение связей между подсистемами – это отражение направлений подчиненности. Во втором случае под вершинами понимаются бизнес-процессы компании. Дуги между вершинами – это связи между бизнес-процессами.

В монографии [14] дается описание одного из крупнейших лесопромышленных предприятий Кировской области. Можно утверждать, что такое предприятие является типовым и содержащим максимальное количество функций для лесопромышленных комплексов. В работе [5] рассмотрена задача снижения интегральных структурных рисков такого лесопромышленного комплекса и соответствующим образом описана структура бизнес-процессов. Для задачи, рассматриваемой в настоящей статье, также дадим соответствующее описание.

Предприятие представляет собой акционерное общество, включающее управляющую подсистему, нижний склад, автотранспортную подсистему, ремонтную мастерскую и другие вспомогательные производства. Также на предприятии имеются 1-й лесопункт, 2-й лесопункт и леспромхоз (ЛПХ). Организационно к 1-му лесопункту относятся нижний склад и гараж. Ко 2-му лесопункту относятся узкоколейная железная дорога (УЖД) и ремонтная мастерская. В леспромхоз также входят лесопункты – 3-й и 4-й. К 3-му лесопункту относятся нижний склад и железнодорожная станция. К 4-му лесопункту относятся автотранспортная подсистема и железнодорожная станция.

Представим формально модель организационной структуры – Sm –предприятия в виде параметрического ориентированного графа, являющегося разновидностью функционального параметрического ориентированного графа, который описывается в виде следующего выражения:

S_m = <<U,D>,Y,H,T> , (1)

где H = <U, D> – когнитивная карта, имеющая вид знакового ориентированного графа;

U – множество концептов;

концепты (вершины) u_iÎU, i = 1,2, …, m – это элементы рассматриваемой системы;

D – множество дуг;

дуга d_ijÎD, ij = 1, 2, …, m показывают связи между вершинами u_i и u_j , Y: U ® T, Y – множество параметров концептов, Y= {Y(u_i) |Y(u_j) ÎY, i=1,2, …, m}, Y(u_i) = {yⁱ_α}, α = 1,2,…,l, yⁱ_α – α – параметр концепта u_i;

T – пространство параметров вершин;

H= H (Y, D) = h (y_i, y_j, d_ij) – функционал преобразования дуг, где h_ij – функция связи параметров концептов, соответствующая каждой дуге, которая может быть детерминированной или стохастический функцией. В простейшем случае h_ij – весовой коэффициент k_ij, т.е. в матрице функционального графа могут быть блоки (подграфы) в виде когнитивной карты (знаковый ориентированный граф), блоки типа «взвешенный граф» с отношениями k_ij, «функциональные» блоки с отношениями типа функция h (y_i, y_j, d_ij).

Упрощенная модель организационной структуры лесопромышленного предприятия представлена на рисунке 1.

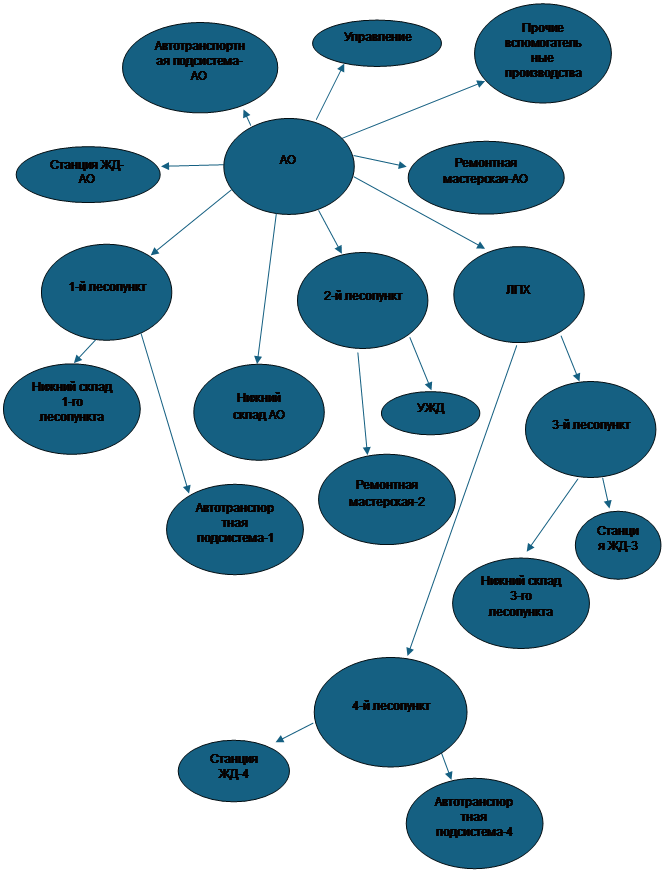
Рисунок 1. Упрощенная модель организационной структуры

лесопромышленного предприятия

Источник: составлено автором.

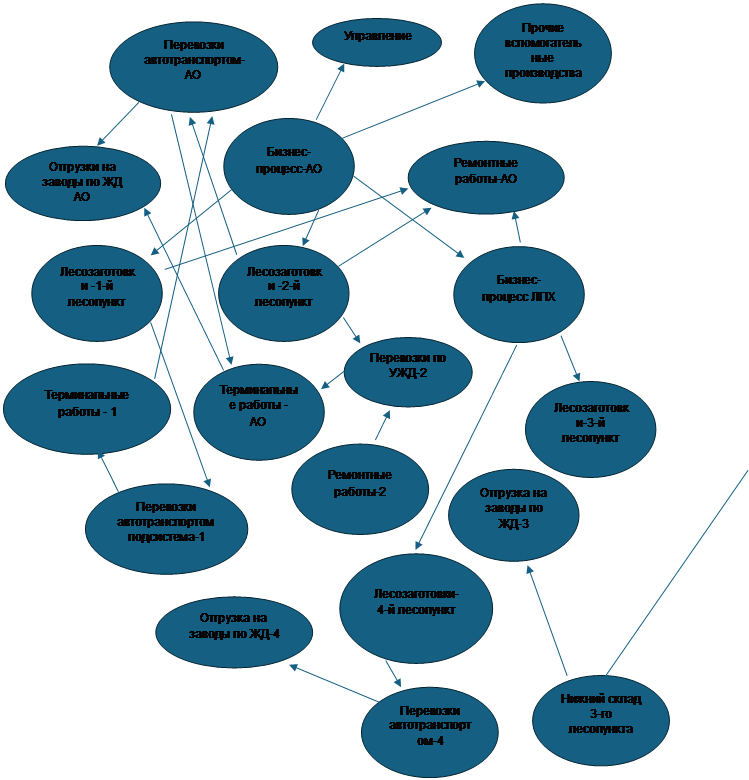
Сделаем преобразования исходного графа, объединяя организационные подсистемы в соответствии с бизнес-процессами предприятия. Получим новую модель предприятия, теперь уже модель бизнес-процессов.

Формально эту модель Bn – предприятия также можно представить в виде параметрического ориентированного графа:

B_n = <<W, F>, Z, G, R>, (2)

где H = <W, F> – когнитивная карта, представляющая собой знаковый ориентированный граф;

W – множество концептов;

концепты (вершины) w_iÎW, i = 1,2, …, l представляют собой элементы исследуемой системы;

F – множество дуг;

дуга f_ijÎF, ij = 1, 2, …, n отражает взаимосвязь между вершинами w_i и wj Z: W ® R , Z – множество параметров концептов, Z= {Z(w_i) |Z(wv_j) ÎZ, i=1,2, …, l }, Z(w_i) = {zⁱ_h}, h = 1, 2, …, m, zⁱ_h – h – параметр концепта w_i;

R – пространство параметров вершин;

G= G (Z, F) = g (z_i, z_j, f_ij) – функционал преобразования дуг, где g_ij – зависимость, отражающая взаимосвязь параметров концептов, соответствующая каждой дуге, которая может быть детерминированной или стохастический функцией. В простейшем случае g_ij – весовой коэффициент x_ij, т.е. в матрице функционального графа могут быть блоки (подграфы) в виде когнитивной карты (знаковый ориентированный граф), блоки типа «взвешенный граф» с отношениями x_ij, «функциональные» блоки с отношениями типа функция g (z_i, z_j, f_ij).

Представим модель бизнес-процессов предприятия графически (рис. 2).

Рисунок 2. Упрощенная модель бизнес-процессов лесопромышленного предприятия

Источник: составлено автором.

На рисунке 2 представлено три уровня бизнес-процессов. Верхний (первый) уровень – уровень акционерного общества. К этому уровню относятся процессы управления АО и прочие вспомогательные производства.

Ко второму уровню отнесем процессы, реализуемые первым лесопунктом, вторым лесопунктом и леспромхозом.

К третьему уровню отнесем процессы, реализуемые первым, вторым, третьим и четвертым лесопунктами. Также к третьему уровню отнесем процессы, реализуемые подсистемами, находящимися в непосредственном подчинении управления первым, вторым лесопунктами и леспромхозом. Кроме подсистем, находящихся в непосредственном подчинении у руководства первого, второго лесопунктов и леспромхоза, к третьему уровню иерархии бизнес-процессов отнесем подсистемы, находящиеся в организационном подчинении у управления акционерного общества, но фактически задействованные в бизнес-процессах второго уровня. К таким подсистемам отнесем автотранспортную подсистему акционерного общества, железнодорожную станцию акционерного общества и ремонтную мастерскую акционерного общества.

Предполагаем, что соответственно иерархии бизнес-процессов предприятия сформирована и система управления

Функционирование предприятия осуществляется следующим образом. Задачей лесопунктов является заготовка древесины и размещение ее на верхних складах. Заготовленная древесина транспортируется с помощью автотранспортной подсистемы и железной дороги на нижние склады. Кроме того, круглые сортименты и пиломатериалы могут приобретаться у мелких лесозаготовителей. Затем древесина подвергается переработке при необходимости и поставляется потребителям по железной дороге или автомобильным транспортом транспортных компаний.

Управление поступлениями на склад и отгрузками со склада осуществляется таким образом, чтобы остатки на складах минимально отличались от заданного уровня. В таблице 1 показана динамика поступлений на нижние склады и отгрузок лесоматериалов в течение одного года (2023 г.).

Таблица 1. Динамика поступлений и отгрузок лесоматериалов в течение года в кбм.

Объемы лесоматериалов	Месяц
	Янв.	Фев.	Мар.	Апр.	Май	Июн.	Июл.	Авг.	Сен.	Окт.	Ноя.	Дек.
Объем остатков лесоматериалов на нижних складах	3000	2744	2880	3222	5310	10276	18918	3000	3000	3000	3000	3000
Поступления на нижние склады	34100	26100	25900	21150	16000	18150	22760	25000	26900	27800	29500	34600
Отгрузки с нижних складов	34356	25964	25558	19062	11034	9508	38678	25000	26900	27800	29500	34600
Изменения остатков на складах	-256	136	342	2088	4966	8642	-15918	0	0	0	0	0
Скорость изменения остатков на складах	-	392	206	1746	2878	3676	-24560	15918	0	0	0	0

Источник: составлено автором.

В работе [3] рассмотрена модель управления экономической системой, в которой управляющие импульсы формируются на верхнем иерархическом уровне с использованием обратной связи, отражающей отклонение остатков продукции на складах от требуемого уровня.

Модель В.И. Арнольда для трехуровневого управления формируется следующим образом.

Пусть:

X – целевой объем количества продукции;

x (t) – объем предложения продукции в интервале t; t+dt;

y (t) – изменение предложения продукции за время dt;

z (t) – скорость изменения предложения продукции за время dt;

k – положительный коэффициент;

dt – шаг времени.

Изменения характеристик экономической системы подчиняются следующим соотношениям:

x(t + dt) = x(t) + y(t) dt; (3)

y(t + dt) = y(t) + z(t) dt. (4)

Задача заключается в том, чтобы, зная отклонение предложения от целевого уровня, таким образом управлять скоростью изменения предложения, чтобы объем предложения был как можно ближе к цели.

Такое управление будем формировать автоматически, увеличивая или уменьшая скорость изменения предложения пропорционально отклонению предложения от спроса на основе отрицательной обратной связи:

z(t + dt) = z(t) – k (x(t) – X) dt. (5)

Переходя в соотношениях (3) – (5) к пределу при dt → 0 получим

dx /dt = y,

dy / dt = z,

dz / dt = - k (x – X).

Делая подстановки получим

x⁽³⁾ = - k (x – X).

Или, вводя замену H=x-X,

H⁽³⁾ = - k H.

Анализ решений данного уравнения показывает, что система управления, основанная на формировании управляющего импульса на основе оценки состояния системы на верхнем уровне иерархии, является неустойчивой.

Для общности представления системы управления рассматриваемой экономической системы предположим, что возможности управления на основе оценки состояния системы существуют на всех уровнях управления. Для этого введем отрицательную обратную связь на каждом иерархическом уровне.

Тогда модель управления будет выглядеть следующим образом.

x(t + dt) = x(t) + y(t) dt – k_x (x(t) – X) dt ; (6)

y(t + dt) = y(t) + z(t) dt – k_y (x(t) – X) dt ; (7)

z(t + dt) = z(t) – k_z (x(t) – X) dt. (8)

Параметрами управления в полученной модели являются коэффициенты k_x, k_y, k_z. Найдем значения этих управляющих параметров, соответствующие данным, представленным в таблице 2. При этом потребуем, чтобы остатки на складе стремились к 0 и введем страховочный объем в размере 3000 кбм.

Таблица 2. Динамика поступлений и отгрузок лесоматериалов в течение года в кбм.

Объемы лесоматериалов	Месяц
	Янв.	Фев.	Мар.	Апр.	Май	Июн.	Июл.	Авг.	Сен.	Окт.	Ноя.	Дек.
Объем остатков лесоматериалов на нижних складах	0	-256	-120	222	2310	7276	15918	0	0	0	0	0
Поступления на нижние склады	34100	26100	25900	21150	16000	18150	22760	25000	26900	27800	29500	34600
Отгрузки с нижних складов	34356	25964	25558	19062	11034	9508	38678	25000	26900	27800	29500	34600
Изменения остатков на складах	-256	136	342	2088	4966	8642	-15918	0	0	0	0	0
Скорость изменения остатков на складах	-	392	206	1746	2878	3676	-24560	15918	0	0	0	0

Примечание: страховочный объем равен 3000 кбм.

Источник: составлено автором.

Для определения коэффициентов k_x, k_y, k_z воспользуемся методом наименьших квадратов. В таблице 3 представлены значения коэффициентов, в наибольшей степени соответствующие данным таблицы 2

Таблица 3. Значения коэффициентов управления, в наибольшей степени

соответствующие данным таблицы 2

Принцип формирования управляющих импульсов	kx	ky	kz
Управляющие импульсы формируются на верхнем иерархическом уровне	0	0	0,2
Управляющие импульсы формируются на всех иерархических уровнях	0,5	0,9	0,01
	0,5	0,9	0,1
	0,5	1,0	0,1
	0,7	0,8	0,3
	0,7	0,8	0,4
	0,7	0,8	0,5
	0,7	0,9	0,2
	0,7	0,8	0,3
	0,8	0,7	0,6
	0,8	0,8	0,5

Источник: составлено автором.

Теперь потребуем, чтобы остатки на складах не стремились к нулю, а стремились к ненулевой величине. Примем эту величину равной страховому объему в 3000 кбм. Также управление в модели осуществляется выбором коэффициентов k_x, k_y, k_z. Значения коэффициентов найдем в соответствии с данными таблицы 1.

Значения коэффициентов k_x, k_y, k_z также найдем методом наименьших квадратов. В таблице 4 представлены значения коэффициентов, в наибольшей степени соответствующие данным таблицы 1.

Таблица 4. Значения коэффициентов управления, в наибольшей степени

соответствующие реальным данным

Принцип формирования управляющих импульсов	kx	ky	kz
Управляющие импульсы формируются на верхнем иерархическом уровне	0	0	0,1
Управляющие импульсы формируются на всех иерархических уровнях	0,4	0,2	0,2
	0,4	0,3	0,2
	0,5	0,2	0,3
	0,6	0,1	0,4

Источник: составлено автором

Теперь перейдем в соотношениях (6) – (8) к пределу при dt → 0 и получим следующую систему дифференциальных уравнений:

dH /dt = y – k_xH,

dy / dt = z - k_yH,

dz / dt = - k_z H.

Или

d³H/dt³ + k_x d²H/dt² + k_y dH/dt + k_zH = 0.

Это уравнение решается явно, а устойчивость желаемого стационарного состояния (x = X, y = z = … = 0) определяется знаком вещественных частей корней характеристического уравнения.

Если вещественные части корней лежат в левой полуплоскости плоскости Re × Im, то решение уравнения устойчиво. Если же хотя бы один из корней находится в правой полуплоскости (Im > 0), то решение уравнения неустойчиво.

Рассмотрим однородное линейное дифференциальное уравнение с постоянными коэффициентами. Тогда в соответствии с [8, с. 483] для того, чтобы все корни характеристического многочлена такого дифференциального уравнения имели отрицательные вещественные числа, необходимо и достаточно, чтобы характеристический многочлен являлся многочленом Гурвица.

Для нашего случая системы управления трех уровней для устойчивости экономической системы необходимо и достаточно соблюдение условий: k_x > 0, k_y > 0, k_z >0, k_x k_y > k_z.

Эти условия означают, что права на управление производством имеются не только у руководителей компании верхнего уровня иерархии, но также и у руководителей остальных иерархических уровней. Однако необходимо отметить, что для реальных предприятий чем больше прав предоставляется нижним иерархическим уровням, тем больше риск ошибок и злоупотреблений различного рода.

Поэтому рассмотрим задачу обеспечения устойчивости системы при минимизации полномочий нижних иерархических уровней. Для оценки полномочий нижних иерархических уровней используем два вида критериев:

– доля решений в %, принимаемых самостоятельно, от общего объема решений, принимаемых на соответствующем уровне иерархии (G_x и G_y);

– объем решений в % (V_x и V_y), принимаемых самостоятельно, от целевого объема лесопродукции X.

Т.е., G_x = max_t |k_x (x(t) – X) | / (|y(t)| + |k_x (x(t) – X)|); G_y = max_t |k_y (x(t) – X) | / (|z(t)| + |k_y (x(t) – X)|);

V_x = max_t|k_x (x(t) – X)| / X ; V_y = max_t|k_y (x(t) – X)| / X,

где t – время. Предполагается, что время t рассматривается на достаточно большом временном интервале.

Тогда для оценки уровня полномочий найдем:

Min_k G_x и Min_k G_y, Min_k V_x и Min_k V_y,

где k = (k_x, k_y, k_z), 0 ≤ k_x ≤ 1, 0 ≤ k_y ≤ 1, 0 ≤ k_z ≤ 1.

В таблице 5 показаны доли решений, принимаемых самостоятельно на низших иерархических уровнях от общего объема решений, и объемы решений, принимаемых самостоятельно, от целевого объема лесоматериалов на нижних складах. При этом будем рассматривать только такие значения коэффициентов, для которых моделируемое отклонение от целевого значения остатков на складах предприятия не оказывается слишком большим (не превышает заданного значения). Это ограничение выявляется путем моделирования с использованием моделей, в наилучшей степени соответствующей реальным данным (приведены выше).

Таблица 5. Доли решений, принимаемых самостоятельно на низших иерархических уровнях от общего объема решений на соответствующих уровнях, и объемы решений, принимаемых самостоятельно, от целевого объема лесоматериалов на нижних складах

Отклонение в % фактического объема продукции x от целевого объема X	Доля решений, принимаемых самостоятельно, от общего объема решений, в %,		Объем решений, принимаемых самостоятельно, в % от целевого объема		Коэффициенты			Примечания
Макct |x-X|	Максt Gx	Максt Gy	Максt |Kx(x-X)|	Максt |Ky(x-X)|	Kx	Ky	Kz
221	100	100	133	89	0,6	0,4	0,1
172	90	90	70	30	0,7	0,3	0,1	Минk Максt |Kx(x-X)|
184	100	100	70	40	0,7	0,4	0,1	МинkМаксt |Kx(x-X)|
194	100	100	70	50	0,7	0,5	0,1	МинkМаксt |Kx(x-X)|
175	100	90	140	35	0,8	0,2	0,1
160	100	100	80	30	0,8	0,3	0,1
175	100	100	80	50	0,8	0,5	0,1
179	90	100	80	60	0,8	0,6	0,1
181	90	100	86	75	0,8	0,7	0,1
143	90	100	90	20	0,9	0,2	0,1	МинkМаксt |Ky(x-X)|
150	90	90	90	30	0,9	0,3	0,1
155	100	100	90	40	0,9	0,4	0,1
159	100	100	90	50	0,9	0,5	0,1
202	100	90	90	50	0,9	0,5	0,2
160	100	100	90	60	0,9	0,6	0,1
182	100	100	90	60	0,9	0,6	0,2
159	100	100	90	70	0,9	0,7	0,1
181	90	100	100	78	0,9	0,7	0,2
156	100	100	95	85	0,9	0,8	0,1
136	100	100	100	20	1,0	0,2	0,1	МинkМаксt |Ky(x-X)|
141	90	100	100	30	1,0	0,3	0,1
144	100	100	100	40	1,0	0,4	0,1
145	100	100	100	50	1,0	0,5	0,1
165	90	100	100	50	1,0	0,5	0,2
144	90	90	100	60	1,0	0,6	0,1
164	100	100	100	60	1,0	0,6	0,2
141	100	100	100	70	1,0	0,7	0,1
161	100	100	100	70	1,0	0,7	0,2
136	100	100	100	80	1,0	0,8	0,1
156	80	100	100	80	1,0	0,8	0,2	МинkМаксt Gx
129	100	100	100	90	1,0	0,9	0,1	МинkМаксt |x-X|
149	100	100	112	101	1,0	0,9	0,2
156	100	100	156	156	1,0	1,0	0,1
K= (Kx, Ky, Kz)

Источник: составлено автором.

Анализ таблицы 5 показывает, что доля решений, принимаемых на низших иерархических уровнях самостоятельно, составляет 90-100% от общего объема решений соответствующего уровня. Объем решений, принимаемых самостоятельно на низших иерархических уровнях составляет не менее 70% от целевого объема лесопродукции. Отсюда следует, что снижение риска злоупотреблений путем структурирования прав практически неосуществимо.

Сравним теперь характеристики модели, в наилучшей степени соответствующей реальным данным, и характеристики модели, обеспечивающей устойчивость управления экономической системой. Значения коэффициентов модели, обеспечивающие наилучшее приближение к реальным данным по методу наименьших квадратов и в то же время обеспечивающие асимптотическую устойчивость системы, демонстрировали слишком высокий уровень отклонения от целевого уровня остатков лесоматериалов на складах.

При этом отличие точности приближения к реальным данным результатов моделирования при нулевом целевом объеме остатков лесоматериалов на складах, когда коэффициенты модели обеспечивают асимптотическую устойчивость и допустимый размер колебаний остатков лесопродукции, от наилучшей точности приближения, которая оценивается методом наименьших квадратов, составляет от 4 до 19%. Отличие точности приближения к реальным данным результатов моделирования, обеспечивающих асимптотическую устойчивость и допустимый размер колебаний остатков лесопродукции, при ненулевом целевом объеме остатков лесоматериалов на складах, от наилучшей точности приближения, полученной методом наименьших квадратов, составляет от 56 до 219%.

Заключение

Таким образом, рассмотрена задача моделирования устойчивости развития производственной системы. Объектом рассмотрения является предприятие лесопромышленного комплекса, выполняющего в качестве основных функций лесозаготовительные работы, приобретение лесоматериалов у мелких лесозаготовителей, транспортировку лесоматериалов с верхних складов на нижние, складирование и отгрузку лесной продукции на перерабатывающие заводы.

Получены значения коэффициентов модели, обеспечивающие устойчивость системы при выполнении ограничений на уровень отклонения остатков на складах, от целевого значения.

Выявлено, что лучшую точность соответствия реальным данным результатов моделирования, обеспечивающих асимптотическую устойчивость системы и требуемый уровень отклонения от целевого объема остатков лесопродукции на складах, дает модель с нулевым целевым объемом остатков и страховочным резервом.

С использованием аппарата дифференциальных уравнений сделана оценка минимального уровня риска злоупотреблений в компании. Данная оценка дает основание заключить, что снижение такого риска не обеспечивается распределением управленческих прав по иерархическим уровням, поскольку концентрация управленческих функций на верхнем уровне иерархии повышает риск потери устойчивости.