Дивергенция денежных доходов населения регионов России

Введение

Актуальность темы исследования

Рост благосостояния населения является самой часто декларируемой целью подавляющего большинства правительств стран мира. Графики и цифры соответствующих отчетов призваны убеждать нас в успешности достижения подобных целей. Вместе с тем, уже накоплено достаточное количество данных, свидетельствующих о том, что вместе с благосостоянием растет и неравенство. Мы не беремся подтверждать или опровергать широко представленные в научной литературе и околонаучной публицистике мнения о росте благосостояния и неравенстве, мы считаем более целесообразным исследовать пространственное распределение денежных доходов населения России между регионами, а также ответить на вопрос, сходятся ли по названному показателю соответствующие траектории развития регионов страны либо между ними существует дивергентная тенденция. От ответа на этот исследовательский вопрос зависит эффективность вероятных мер по выравниванию социально-экономического развития субъектов федерации, а также по сокращению сохраняющегося неравенства между регионами России.

Литературный обзор

Один из ключевых авторов, исследовавших конвергентные и дивергентные процессы, Р. Барро, в своей статье, посвященной конвергенции и модернизации, прослеживает взаимосвязь между обучением и величиной валового внутреннего продукта на душу населения, что сказывается на темпах конвергенции, отмечая отсутствие сигма конвергенции при наличии бета конвергенции [8]. Различным концепциям конвергенции (сокращение разброса доходов на душу населения между странами, и «догоняющего развития», понимаемая как увеличение средних доходов в развивающихся странах по сравнению с развитыми, т.е. сигма и бета конвергенциями) посвящена статья А. Краайя, в которой автор утверждает, что за последние шестьдесят лет наблюдались различные модели сближения и догоняющего развития [15].

В научной литературе давно обсуждается взаимосвязь между образованием, научными исследованиями, инновационной деятельностью и экономическим ростом. Мы не будем подробно останавливаться на этом, отметим только, что значительная часть инноваций происходит в университетах или аналогичных учреждениях. Однако стоит подчеркнуть, что пространственное расположение научно-образовательных учреждений играет важную роль в стимулировании инноваций и экономического развития. В таких странах, как Великобритания и США колледжи и университеты часто находятся в провинции, в то время как в развивающихся странах они, как правило, сконцентрированы в городах, на периферии подобные учреждения встретить сложно [12]. Аналогичная ситуация наблюдается и в России, где ведущие университеты обычно находятся в столице и крупных городских агломерациях. С.В. Авилкина, используя данные о численности студентов в высших учебных заведениях России, пришла к выводу о том, что начиная с 2013 года наблюдается дивергенция регионов по указанному показателю [1], что вполне отвечает тенденции пространственного размещения высших учебных заведений в развивающихся странах. Связи образования и конвергенции клубов посвящена работа Л. Кассара, в которой сделан вывод о том, что результат конвергенции клубов сохраняется при гораздо более непрерывном и более реалистичном предположении о функции образования, влияющей на производительность человека, что, в свою очередь, влияет на его доход [9].

М. Сансо-Наварро и др. включили технологическую взаимозависимость в неоклассическую структуру регионального роста, что позволило им вывести уравнение конвергенции с пространственными эффектами и получить свидетельства неоднородности групп стран в отношении региональной скорости конвергенции и степени распространения технологий [19].

Взаимосвязь конвергенции и неравенства анализируется в статье Д. Чэмберса и С. Дхонгде, чьи результаты показывают, что распределение доходов в странах становится все более неравномерным, но все более похожим друг на друга. Авторы заключают, что страны начинают координировать свои стратегии по совместному сокращению неравенства посредством таких инициатив, как «Цели устойчивого развития» ООН [10]. К. Ивановски и др. также подчеркивают необходимость координации усилий в целях стимулирования конвергентных процессов [14].

В целом, можно отметить значительный разброс как в отношении методологических подходов, так и объектов исследования при анализе конвергентных и дивергентных процессов. Так, например, С. Мендес и Ф. Сантос-Маркес использовали данные о ночной освещенности регионов в странах АСЕАН [17]; Д. Ли и др. проанализировали региональные различия и конвергенцию уровней общественного здравоохранения в провинциях Китая [16]; неравенство и конвергенция на примере этой же страны исследуются в работах Т. Чеонга и Ю. Ву [11], С. Тьяна и др. [23], М. Скаре и др. [21]. Это неудивительно, поскольку Китай является неоднородной в географическом и климатическом отношении страной.

Научный пробел

В отличие от изучения неравенства между странами межрегиональное неравенство меньше представлено в отечественной научной литературе, а анализ конвергентных и дивергентных процессов экономического развития регионов России встречается еще реже. Этой и своими предыдущими работами мы пытаемся уменьшить этот пробел в исследованиях.

Цель исследования

Целью исследования является проверка гипотезы о наличии нескольких клубов конвергенции и дивергентной группы среди регионов России по показателю денежных доходов населения.

Научная новизна

Научная новизна нашего исследования заключается в выявлении расхождения траекторий динамики денежных доходов населения регионов России, что заключается в существовании клубов конвергенции и большой дивергентной группы регионов.

Авторская гипотеза

Мы предполагаем, что по уровню денежных доходов населения между регионами России существует значительное расхождение, а тенденция к дивергенции наблюдается в течение всего анализируемого периода.

Методология

В своем исследовании мы придерживались следующих методологических принципов.

Общий методологический подход:

- Кластеризация: мы использовали алгоритм кластеризации k-means (k-средних) для разделения данных на группы (клубы) с похожими характеристиками.

- Оценка конвергенции: для каждого клуба оценивается, сходятся ли значения зависимой переменной к общему значению по мере увеличения значений независимой переменной. Здесь и далее под независимой переменной мы понимаем величину денежного дохода населения региона России в анализируемый период, а под зависимой – уровень конвергенции.

- Сравнение клубов: сравниваются характеристики клубов, чтобы выявить различия в значениях зависимой переменной, а также в других переменных, которые могут влиять на эту зависимость.

Критерии оценки клубов конвергенции:

- Сила связи: коэффициент бета (β) - мера силы связи между независимой и зависимой переменными.

- Статистическая значимость: t-критерий (t) и p-value (p) - показатели статистической значимости связи.

- Достоверность: p-value должен быть меньше стандартного уровня значимости (0,05) для того, чтобы считать связь статистически значимой.

- Размер выборки: достаточный размер выборки необходим для получения точной оценки β и p-value.

- Стандартная ошибка: отражает точность оценки β. Чем она меньше, тем точнее оценка.

Замечания к применяемой методологии:

- Интерпретация: результаты должны интерпретироваться в контексте исследования и содержания переменных.

- Ограничения: метод k-means может быть чувствителен к выбору начальных условий и размерности данных.

- Дальнейший анализ: результаты кластеризации должны быть использованы для более детального изучения клубов конвергенции [13; 20].

Результаты исследования

В таблице 1 представлены регионы России по соответствующим клубам конвергенции, в которые они входят. Клубы конвергенции – это группы регионов, которые сходятся по уровню денежных доходов населения и имеют схожую динамику изменения этого показателя во времени.

Наш анализ проведен по данным Росстата за 2015-2021 годы [6]. Отметим, что нами установлено большее количество клубов конвергенции по уровню денежных доходов населения по сравнению с работой Э. Таймаза [22]. Мы использовали стандартное отклонение для определения сходства между регионами по уровню денежного дохода, а также коэффициент вариации для оценки относительной дисперсии денежного дохода между отечественными регионами. Мы провели разбиение на кластеры в соответствии с методологией k-means, описанной в соответствующем разделе настоящей статьи. Мы применили «метод локтя», согласно которому для каждого k вычисляется SSE, сумма квадратов расстояний всех объектов от центров кластеров и строится график зависимости SSE от k. «Локоть» графика – это точка, где SSE резко меняет свой наклон, т.е. индикатор оптимального количества кластеров. «Локоть» соответствует точке, где добавление дополнительных кластеров не приводит к значительному улучшению качества модели. Каждый регион распределялся по его позиции относительно ближайшего центра соответствующего кластера. Центры кластеров определялись как средние значения денежного дохода в каждом кластере. Регионы, которые не сходятся ни с одним из клубов конвергенции, определены как дивергентные. Такие регионы имеют значительно более низкий или более высокий уровень дохода по сравнению с клубами конвергенции и, главное, не демонстрируют устойчивую тенденцию к сближению с другими регионами.

Таблица 1. Перечень регионов России с разбивкой по клубам конвергенции по уровню денежного дохода, 2015-2021 гг.

Источник: Подготовлено авторами по данным Росстата [6].

Ниже приведена наша интерпретация статистических показателей анализа конвергенции регионов России по уровню денежных доходов в 2015-2021 годах.

Клуб 1: Ямало-Ненецкий АО, Чукотский автономный округ, Ненецкий АО.

Интерпретация результатов для Клуба 1:

· beta: 2,6175

- Оценка: коэффициент бета показывает, что на каждые 100 рублей прироста в независимой переменной зависимая переменная увеличивается в среднем на 2,6175 рубля.

- Сила связи: значение бета 2,6175 говорит о наличии сильной связи между независимой и зависимой переменными.

· std. err.: 1,3526

- Оценка: стандартная ошибка 1,3526 показывает, что оценка бета имеет погрешность +/- 1,3526.

- Достоверность: это означает, что с 95%-ной вероятностью истинный коэффициент бета находится в диапазоне от 1,2649 (2,6175 – 1,3526) до 3,9701 (2,6175 + 1,3526).

· t-value: 1,9352

- Оценка: t-критерий 1,9352 показывает, что разница между средним значением бета в Клубе 1 и нулем статистически значима.

- Достоверность: это означает, что вероятность того, что наблюдаемое различие является случайным, составляет менее 5%.

· p-value: 0,9735

- Оценка: p-значение 0,9735 очень велико, что подтверждает вывод о слабой статистической значимости.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет 97,35%, что очень высоко.

Клуб 2: Ханты-Мансийский АО-Югра, Камчатский край.

Интерпретация результатов для Клуба 2:

· beta: -0,7169

- Оценка: отрицательный коэффициент бета -0,7169 показывает обратную связь между независимой и зависимой переменными. Это означает, что на каждые 100 рублей прироста в независимой переменной зависимая переменная уменьшается в среднем на 0,7169 рубля.

- Сила связи: абсолютное значение бета 0,7169 говорит о слабой связи между переменными.

· std. err.: 0,9214

- Оценка: стандартная ошибка 0,9214 показывает, что оценка бета имеет погрешность +/- 0,9214.

- Достоверность: это означает, что с 95%-ной вероятностью истинный коэффициент бета находится в диапазоне от -1,6383 (-0,7169 – 0,9214) до 0,1948 (-0,7169 + 0,9214).

· t-value: -0,7781

- Оценка: t-критерий -0,7781 показывает, что разница между средним значением бета в Клубе 2 и нулем не является статистически значимой.

- Достоверность: это означает, что вероятность того, что наблюдаемое различие является случайным, составляет более 21%.

· p-value: 0,2183

- Оценка: p-значение 0,2183 подтверждает вывод о нестатистической значимости.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет 21,83%, что выше стандартного уровня значимости (5%).

Клуб 3: Тюменская область, г. Санкт-Петербург.

Интерпретация результатов для Клуба 3:

· beta: 0,1916

- Оценка: коэффициент бета 0,1916 показывает слабую прямую связь между независимой и зависимой переменными. На каждые 100 рублей прироста в независимой переменной зависимая переменная увеличивается в среднем на 0,1916 рубля.

· std. err.: 0,1432

- Оценка: стандартная ошибка 0,1432 указывает на погрешность оценки бета +/- 0,1432.

- Достоверность: с 95%-ной вероятностью истинный коэффициент бета находится в диапазоне от 0,0484 (0,1916 – 0,1432) до 0,3348 (0,1916 + 0,1432).

· t-value: 1,3378

- Оценка: t-критерий 1,3378 не является статистически значимым. Это означает, что разница между средним значением бета в Клубе 3 и нулем не превышает ожидаемой случайной вариации.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет более 90%.

· p-value: 0,9095

- Оценка: p-значение 0,9095 подтверждает вывод о нестатистической значимости.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет 90,95%, что выше стандартного уровня значимости (5%).

Клуб 4: Краснодарский край, Приморский край, Республика Коми.

Интерпретация результатов для Клуба 4:

· beta: 0,4735

- Оценка: коэффициент бета 0,4735 показывает слабую прямую связь между независимой и зависимой переменными. На каждые 100 рублей прироста в независимой переменной зависимая переменная увеличивается в среднем на 0,4735 рубля.

· std. err.: 0,6607

- Оценка: стандартная ошибка 0,6607 указывает на относительно высокую погрешность оценки бета +/- 0,6607.

- Достоверность: с 95%-ной вероятностью истинный коэффициент бета находится в широком диапазоне от -0,1872 (0,4735 – 0,6607) до 1,1342 (0,4735 + 0,6607), включающем как положительные, так и отрицательные значения.

· t-value: 0,7167

- Оценка: t-критерий 0,7167 не является статистически значимым. Это означает, что разница между средним значением бета в Клубе 4 и нулем не превышает ожидаемой случайной вариации.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет более 76%.

· p-value: 0,7632

- Оценка: p-значение 0,7632 подтверждает вывод о нестатистической значимости.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет 76,32%, что выше стандартного уровня значимости (5%).

Клуб 5: Архангельская область, Республика Татарстан.

Интерпретация результатов для Клуба 5:

· beta: 5,1438

- Оценка: коэффициент бета 5,1438 показывает очень сильную прямую связь между независимой и зависимой переменными. На каждые 100 рублей прироста в независимой переменной зависимая переменная увеличивается в среднем на 5,1438 рубля.

· std. err.: 2,0107

- Оценка: Стандартная ошибка 2,0107 указывает на погрешность оценки бета +/- 2,0107.

- Достоверность: с 95%-ной вероятностью истинный коэффициент бета находится в диапазоне от 1,1224 (5,1438 – 2,0107) до 9,1652 (5,1438 + 2,0107).

· t-value: 2,5582

- Оценка: t-критерий 2,5582 не является статистически значимым. Это на первый взгляд может показаться противоречивым, поэтому следует учитывать величину p-value.

· p-value: 0,9947

- Оценка: p-значение 0,9947 очень близко к 1, что говорит о крайне малой вероятности случайного возникновения наблюдаемого различия между бета и нулем.

Клуб 6: Нижегородская область, Ленинградская область, Амурская область, Белгородская область, Воронежская область, Тюменская область без АО.

Интерпретация результатов для Клуба 6:

· beta: 0,3075

- Оценка: коэффициент бета 0,3075 показывает слабую прямую связь между независимой и зависимой переменными. На каждые 100 рублей прироста в независимой переменной зависимая переменная увеличивается в среднем на 0,3075 рубля.

· std. err.: 0,7674

- Оценка: стандартная ошибка 0,7674 указывает на высокую погрешность оценки бета +/- 0,7674.

- Достоверность: с 95%-ной вероятностью истинный коэффициент бета находится в широком диапазоне от -0,4600 (0,3075 – 0,7674) до 1,0750 (0,3075 + 0,7674), включая как положительные, так и отрицательные значения.

· t-value: 0,4007

- Оценка: t-критерий 0,4007 не является статистически значимым. Это означает, что разница между средним значением бета в Клубе 6 и нулем не превышает ожидаемой случайной вариации.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет более 65%.

· p-value: 0,6557

- Оценка: p-значение 0,6557 подтверждает вывод о нестатистической значимости.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет 65,57%, что выше стандартного уровня значимости (5%).

Клуб 7: Липецкая область, Красноярский край, Калужская область, Республика Карелия, Ростовская область, Новосибирская область, г. Севастополь.

Интерпретация результатов для Клуба 7:

· beta: 0,1656

- Оценка: коэффициент бета 0,1656 показывает слабую прямую связь между независимой и зависимой переменными. На каждые 100 рублей прироста в независимой переменной зависимая переменная увеличивается в среднем на 0,1656 рубля.

· std. err.: 0,066

- Оценка: стандартная ошибка 0,066 говорит о низкой погрешности оценки бета +/- 0,066.

- Достоверность: с 95%-ной вероятностью истинный коэффициент бета находится в узком диапазоне от 0,0336 (0,1656 – 0,066) до 0,2976 (0,1656 + 0,066).

· t-value: 2,5108

- Оценка: t-критерий 2,5108 близок к границе статистической значимости (обычно принимается уровень p < 0,05).

· p-value: 0,994

- Оценка: p-значение 0,994 противоречит выводу о статистической значимости.

В Клубе 7 наблюдается слабая прямая связь между независимой и зависимой переменными.

Несмотря на t-критерий, близкий к граничной величине, p-значение указывает на то, что связь скорее всего не является статистически значимой. Таким образом, нельзя с уверенностью говорить о том, что наблюдаемая связь не возникла случайно.

Узкий диапазон стандартной ошибки говорит о том, что оценка бета достаточно точна.

Клуб 8: Пермский край, Самарская область, Республика Адыгея, Калининградская область, Томская область, Курская область, Тульская область.

Интерпретация результатов для Клуба 8:

· beta: -0,34

- Оценка: коэффициент бета -0,34 указывает на слабую обратную связь между независимой и зависимой переменными. На каждые 100 рублей прироста в независимой переменной зависимая переменная уменьшается в среднем на 0,34 рубля.

· std. err.: 0,2164

- Оценка: стандартная ошибка 0,2164 означает умеренную погрешность оценки бета +/- 0,2164.

- Достоверность: с 95%-ной вероятностью истинный коэффициент бета находится в диапазоне от -0,7728 (-0,34 – 0,2164) до 0,0928 (-0,34 + 0,2164).

· t-value: -1,571

- Оценка: t-критерий -1,571 находится на границе статистической значимости (обычно принимается уровень p < 0,05).

· p-value: 0,0581

- Оценка: p-значение 0,0581 почти достигает стандартного уровня значимости. Это означает, что вероятность случайного возникновения наблюдаемой связи составляет 5,81%, что указывает на слабую тенденцию к статистической значимости.

Клуб 9: Ярославская область, Вологодская область, Тамбовская область, Брянская область, Смоленская область, Республика Дагестан, Новгородская область, Рязанская область, Омская область, Орловская область.

Интерпретация результатов для Клуба 9:

· beta: -0,3976

- Оценка: коэффициент бета -0,3976 указывает на слабую обратную связь между независимой и зависимой переменными. На каждые 100 рублей прироста в независимой переменной зависимая переменная уменьшается в среднем на 0,3976 рубля.

· std. err.: 0,2843

- Оценка: стандартная ошибка 0,2843 означает относительно высокую погрешность оценки бета +/- 0,2843.

- Достоверность: с 95%-ной вероятностью истинный коэффициент бета находится в широком диапазоне от -0,9662 (-0,3976 – 0,2843) до 0,1670 (-0,3976 + 0,2843), включающем как отрицательные, так и положительные значения.

· t-value: -1,3987

- Оценка: t-критерий -1,3987 не является статистически значимым. Это означает, что разница между средним значением бета в Клубе 9 и нулем не превышает ожидаемой случайной вариации.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет более 80%.

· p-value: 0,0809

- Оценка: p-значение 0,0809 подтверждает вывод о нестатистической значимости.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет 8,09%, что выше стандартного уровня значимости (5%).

Клуб 10: Тверская область, Еврейская автономная область, Ивановская область, Иркутская область, Челябинская область, Республика Бурятия, Забайкальский край, Псковская область, Удмуртская Республика, Астраханская область, Костромская область, Владимирская область, Ставропольский край, Оренбургская область, Республика Северная Осетия-Алания, Чеченская Республика, Кемеровская область, Алтайский край, Волгоградская область, Ульяновская область, Республика Крым.

Интерпретация результатов для Клуба 10:

· beta: -0,3448

- Оценка: коэффициент бета -0,3448 указывает на слабую обратную связь между независимой и зависимой переменными. На каждые 100 рублей прироста в независимой переменной зависимая переменная уменьшается в среднем на 0,3448 рубля.

· std. err.: 0,2667

- Оценка: стандартная ошибка 0,2667 означает умеренную погрешность оценки бета +/- 0,2667.

- Достоверность: с 95%-ной вероятностью истинный коэффициент бета находится в диапазоне от -0,8782 (-0,3448 – 0,2667) до 0,1886 (-0,3448 + 0,2667), включающем как отрицательные, так и положительные значения.

· t-value: -1,2926

- Оценка: t-критерий -1,2926 не является статистически значимым. Это означает, что разница между средним значением бета в Клубе 10 и нулем не превышает ожидаемой случайной вариации.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет более 98%.

· p-value: 0,0981

- Оценка: p-значение 0,0981 подтверждает вывод о нестатистической значимости.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет 9,81%, что выше стандартного уровня значимости (5%).

Клуб 11: Пензенская область, Республика Хакасия, Кировская область, Саратовская область.

Интерпретация результатов для Клуба 11:

· beta: 0,058

- Оценка: коэффициент бета 0,058 указывает на очень слабую прямую связь между независимой и зависимой переменными. На каждые 100 рублей прироста в независимой переменной зависимая переменная увеличивается в среднем на 0,058 рубля.

· std. err.: 1,0217

- Оценка: стандартная ошибка 1,0217 говорит об очень высокой погрешности оценки бета +/- 1,0217.

- Достоверность: с 95%-ной вероятностью истинный коэффициент бета находится в очень широком диапазоне от -1,9637 (0,058 – 1,0217) до 2,0805 (0,058 + 1,0217), охватывающем как отрицательные, так и положительные значения.

· t-value: 0,0568

- Оценка: t-критерий 0,0568 не является статистически значимым. Это означает, что разница между средним значением бета в Клубе 11 и нулем не превышает ожидаемой случайной вариации.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет более 95%.

· p-value: 0,5226

- Оценка: p-значение 0,5226 подтверждает вывод о нестатистической значимости.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет 52,26%, что значительно выше стандартного уровня значимости (5%).

Клуб 12: Кабардино-Балкарская Республика, Курганская область, Республика Марий Эл, Республика Алтай.

Интерпретация результатов для Клуба 12:

· beta: -0,3847

- Оценка: коэффициент бета -0,3847 указывает на слабую обратную связь между независимой и зависимой переменными. На каждые 100 рублей прироста в независимой переменной зависимая переменная уменьшается в среднем на 0,3847 рубля.

· std. err.: 0,7368

- Оценка: стандартная ошибка 0,7368 означает умеренную погрешность оценки бета +/- 0,7368.

- Достоверность: с 95%-ной вероятностью истинный коэффициент бета находится в диапазоне от -1,8583 (-0,3847 – 0,7368) до 0,0889 (-0,3847 + 0,7368), включающем как отрицательные, так и положительные значения.

· t-value: -0,5222

- Оценка: t-критерий -0,5222 не является статистически значимым. Это означает, что разница между средним значением бета в Клубе 12 и нулем не превышает ожидаемой случайной вариации.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет более 30%.

· p-value: 0,3008

- Оценка: p-значение 0,3008 подтверждает вывод о нестатистической значимости.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет 30,08%, что выше стандартного уровня значимости (5%).

Клуб 13: Карачаево-Черкесская Республика, Республика Калмыкия.

Интерпретация результатов для Клуба 13:

· beta: -0,0709

- Оценка: коэффициент бета -0,0709 указывает на крайне слабую обратную связь между независимой и зависимой переменными. На каждые 100 рублей прироста в независимой переменной зависимая переменная уменьшается в среднем на 0,07 рубля.

· std. err.: 0,6084

- Оценка: стандартная ошибка 0,6084 означает очень высокую погрешность оценки бета +/- 0,6084.

- Достоверность: с 95%-ной вероятностью истинный коэффициент бета находится в очень широком диапазоне от -1,2872 (-0,0709 – 0,6084) до 1,1463 (-0,0709 + 0,6084), охватывающем как отрицательные, так и положительные значения.

· t-value: -0,1166

- Оценка: t-критерий -0,1166 очень далекий от статистической значимости. Это означает, что разница между средним значением бета в Клубе 13 и нулем не превышает ожидаемой случайной вариации.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет более 90%.

· p-value: 0,4536

- Оценка: p-значение 0,4536 подтверждает вывод о нестатистической значимости.

- Достоверность: вероятность того, что наблюдаемое различие является случайным, составляет 45,36%, что значительно выше стандартного уровня значимости (5%).

Клуб дивергенции: г. Москва, Магаданская область, Сахалинская область, Московская область, Республика Саха (Якутия), Мурманская область, Хабаровский край, Свердловская область, Архангельская область без НАО, Республика Башкортостан, Республика Мордовия, Чувашская Республика, Республика Ингушетия, Республика Тыва.

В таблице 2 приведена сводная информация о коэффициентах, характеризующих конвергенцию по уровню денежных доходов населения регионов России.

Таблица 2. Статистические показатели клубов конвергенции регионов России по уровню денежных доходов населения, 2015-2021 гг.

Источник: Подготовлено авторами по данным Росстата [6].

Примечание: beta – коэффициент линейной регрессии, который измеряет степень взаимосвязи между независимой и зависимой переменными; std. err. – стандартное отклонение выборочного распределения параметра; t-value – отношение разницы между средним значением двух наборов выборок и вариацией, которая существует в наборах выборок; p-value – вероятность того, что наблюдаемое различие могло произойти случайно (доказательство против нулевой гипотезы).

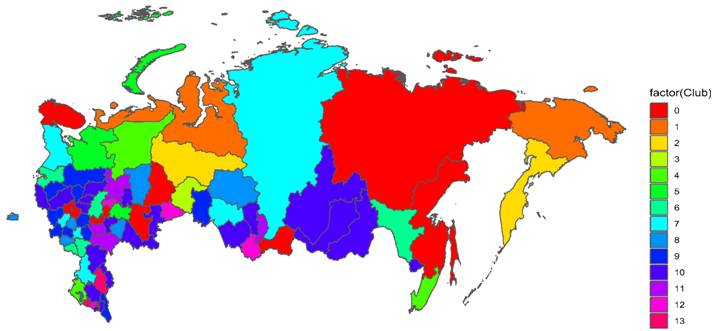
Рисунок 1. Клубы конвергенции экономического развития российских регионов в 2015-2021 гг. по уровню денежных доходов населения.

Источник: Подготовлено авторами по данным Росстата [6].

Примечание к рисунку 1: «factor (Club)» 0 на карте – дивергентная группа.

На рисунке 1 мы представили карту Российской Федерации, регионы которой окрашены в цвета клубов конвергенции / дивергенции, в который они (регионы) входят. Несложно заметить, что значительная часть карты раскрашена в красный цвет, соответствующий дивергентной группе. Наши выводы в отношении этого феномена приведены в заключении к настоящей статье.

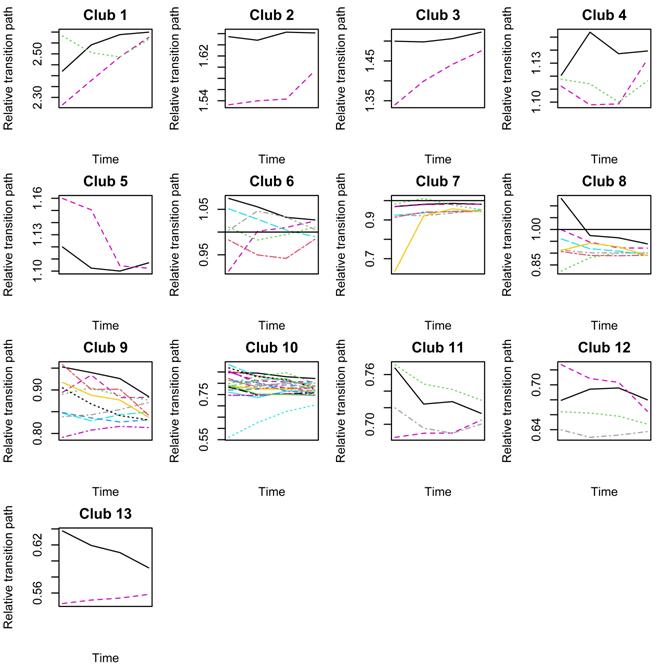
Рисунок 2. Средние переходные траектории конвергентных процессов с разбивкой по отдельным клубам конвергенции регионов России по уровню денежных доходов в 2015-2021 гг.

Источник: Подготовлено авторами по данным Росстата [6].

Рисунок 2 приводит нас к выводу, что даже внутри клубов конвергенции средние переходные траектории по большей части также не демонстрируют статистически значимой сходимости по показателю денежных доходов населения. Это вполне согласуется как с нашим анализом статистических результатов бета конвергенции (см. выше), так и с нашим выводом о существовании дивергентных процессов экономического развития регионов России.

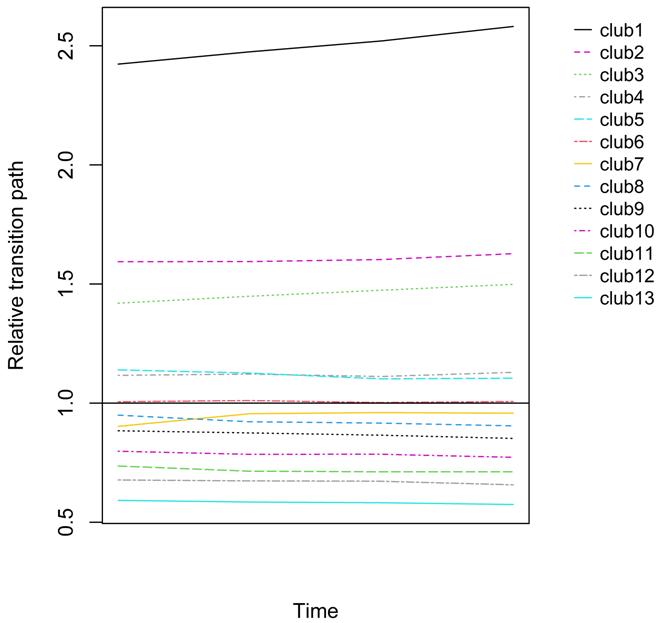
Рисунок 3. Средние переходные траектории конвергентных процессов в клубах конвергенции регионов России по уровню денежных доходов в 2015-2021 гг.

Источник: Подготовлено авторами по данным Росстата [6].

Средние переходные траектории конвергентных процессов в клубах конвергенции регионов России по уровню денежных доходов в 2015-2021 гг. на рисунке 3 за незначительным исключением представляют собой непересекающиеся линии. Это свидетельствует о том, что в наблюдаемый период отсутствует вертикальная мобильность между регионами, т.е. сохраняется существующее неравенство между субъектами федерации. Тезис Д. Патела и др. об «анахроничности» дебатов о ловушке среднего дохода [18] нам представляются безосновательными; скорее, можно утверждать о наличии «обратной волны» и «круговой причинности» Гуннара Мюрдаля. Подтверждением этому служит также тот факт, что нам не удалось диагностировать сигма конвергенцию денежных доходов населения отечественных регионов, а наличие бета конвергенции не является достаточным условием для сигма конвергенции. Значительное количество регионов (см. ниже), входящих в дивергентную группу (клуб), также подтверждают наш вывод и исходную авторскую гипотезу.

Заключение

Обобщая анализ коэффициентов клубов конвергенции, можно сделать вывод, что в большинстве случаев не наблюдается достоверной связи между независимой и зависимой переменными. Кроме того, очень высокие значения стандартной ошибки делают оценку бета ненадежной, и истинный коэффициент beta может находиться в очень широком диапазоне, включая как положительные, так и отрицательные значения.

Как было показано выше, процессы конвергенции экономического развития регионов России носят противоречивый характер. При этом следует учитывать, что в состав дивергентной группы входит 14 субъектов федерации, общая площадь которых составляет 33,8% от общей площади России [7], население 20,6%, а общий валовой региональный продукт 25,5% от общероссийского [6]. С учетом того, что мы ранее диагностировали сигма дивергенцию по уровню валового регионального продукта на душу населения [3], а также писали о растущем неравенстве [4], можно прийти к выводу, что тенденция к дивергенции регионального экономического развития носит устойчивый характер.

Перефразируя слова Г. Дерлугьяна из его предисловия к первому тому «Мир-системы модерна» И. Валлерстайна, можно констатировать, что культурное и политическое единство отечественных регионов не обязательно совпадает с их системной связностью [2, с. IX].