Анализ конвергентных процессов в экономике российских регионов

Введение

Актуальность темы исследования

Неравенство, рассматриваемое нами как частный случай расхождения (дивергенции) регионального развития, является острой проблемой современности, поскольку порождает социальную напряженность, ставя сложные задачи выравнивая территориального социально-экономического развития.

Региональная конвергенция – это концепция, заложенная в теории регионального роста, подробно изложена в обширных исследованиях, проведенном Р. Барро и К. Сала-и-Мартином [11; 12]. Она относится к явлению, характеризующемуся снижением региональных различий со временем.

С позиции региональной экономики, особенно в рамках неоклассической теории роста, ожидается, что региональные различия со временем сократятся. По неоклассической модели роста предполагается, что экономический выпуск данного региона, выраженный такими показателями, как валовой региональный продукт (ВРП) на душу населения, зависит от накопления факторов производства, в частности капитала и труда, как это представлено агрегированной функцией производства. Эта модель основана на предположениях о постоянных отдачах от масштаба и убывающей предельной производительности факторов. Следовательно, регионы, обладающие высоким начальным уровнем развития, обычно испытывают более медленный экономический рост, тогда как те, у которых начальные позиции (ВРП на душу населения) ниже, - более быстрый рост. Это явление обычно называют бета-сходимостью (бета конвергенцией). Традиционно считается, что все регионы в конечном итоге сходятся к одному уровню стабильного регионального выпуска [29, с. R8].

С другой стороны, сигма конвергенция означает постепенное снижение региональных различий в отношении регионального выпуска со временем. М. Абрамовиц назвал сходимость, измеренную уровнями отклонений, «сигма конвергенцией», а сходимость, измеренную тем, насколько бедные страны растут быстрее, чем богатые, - «бета конвергенцией» [8]. Этот концепт разъясняется в работах, таких как работы Н. Оллингтона и Д. Маккомби [9], Р. Капелло и П. Нейкампа (2009) [14].

Литературный обзор

В большинстве случаев авторы проанализированных нами работ говорят о конвергентных или дивергентных процессах между богатыми и бедными странами, реже о подобных процессах внутри стран. Например, У. Баумоль [13] исследовал конвергенцию за столетие, начиная с 1870 года. Тем не менее, гипотеза о конвергенции, которая утверждает, что во-первых, разрыв между бедными и богатыми странами сокращается со временем, и, во-вторых, бедные страны растут с более высокими темпами, чем богатые страны (см., напр., Ф. Агийон и Д. Уильямсон [1]), остается одной из старейших и ключевых противоречий в экономической теории [23, с. 85].

Глобализация облегчила передачу дивергентных процессов внутри стран, что привело к увеличению разрыва между богатыми регионами, ориентированными на экспорт, и регионами, ориентированными на внутренний рынок. Это привело к росту академических исследований по этому вопросу, и несколько исследований предоставили доказательства как конвергенции, так и дивергенции в результате экономического развития регионов.

Например, З. Бакуш и И. Ферто [10] обнаружили доказательства региональной дивергенции, используя концепции бета конвергенции, сигма конвергенции и наличия единичного корня («unit root»). Р. Чейлан и В. Абиев [15] использовали нелинейные и нелинейные асимметричные тесты на наличие долгосрочной или детерминированной конвергенции в пяти странах Европейского союза и стохастической конвергенции в девяти странах ЕС. Д. Чеймберс и С, Дхонгде [16] установили, что относительное распределение доходов развитых стран сходится с более быстрым темпом.

У. Майлз [22] использовал метод, который позволяет учитывать структурные изменения и обнаружил, что общие доказательства сходимости внутри США незначительны. К. Ринз и Й. Ворхейс [24] повторно исследовали последние тенденции в региональной сходимости доходов в США и обнаружили, что доходы штатов стали менее похожими (то есть разошлись).

М. Сансо-Наварро и др. [25] включили технологическую взаимозависимость в неоклассическую модель регионального роста с неполной мобильностью факторов, что привело к уравнению сходимости с пространственными эффектами. Они получили доказательства гетерогенности между группами стран в отношении скорости региональной конвергенции и степени распространения технологий.

Значительное количество исследователей сосредоточили свои усилия на анализе «клубов конвергенции» или кластеров. Например, Л. Коррадо и др. [17] интерпретировали состав полученных кластеров конвергенции, проверяя их на соответствие нескольким возможным группировкам, предложенным современными теориями и гипотезами регионального роста и конвергенции. По очевидным причинам нас особенно интересует исследование Е. Таймаза [27], который проанализировал паттерны роста российских федеральных субъектов и проверил, сходятся ли все регионы к общему пути роста или существует множество клубов конвергенции между регионами России.

Научный пробел

Исследования конвергентных и дивергентных процессов, в основном, связаны с анализом межстранового неравенства, что вполне объяснимо доминированием неоклассического подхода в современной экономической науке. Региональная конвергенция и дивергенция пока что находятся на периферии научного интереса исследователей, занятых настоящей проблематикой, хотя следует отметить рост числа публикаций, посвященных, как правило, расхождению регионального развития провинций Китая и европейских регионов. Мы вынуждены констатировать недостаточное количество исследований конвергентных и дивергентных процессов в экономике российских регионов, несмотря на появление интересных работ отечественных ученых в этой области [2; 3; 5; 6].

Цель исследования

Основной целью настоящей статьи является исследование процессов конвергенции экономики российских регионов в период с 2005 по 2020 г. Мы также провели сравнительный анализ полученных результатов между собой, чтобы проследить динамику изменения конвергентных процессов в названный период.

Научная новизна

Научная новизна нашего исследования заключается в диагностике дивергентных процессов в экономике российских регионов на основе анализа скорости гармонизации уровня валового регионального продукта на душу населения и проверки наличия сигма конвергенции, рассматриваемой как снижение уровня межрегионального неравенства по названному показателю.

Авторская гипотеза

Наша гипотеза состоит в том, что конвергентные процессы наличествуют в экономике российских регионов, однако скорость гармонизации уровней валового регионального продукта на душу населения остается крайне низкой на всем анализируемом периоде – с 2005 по 2020 гг. Кроме того, мы считаем, что несмотря на рост ВРП на душу населения в российских регионах уровень межрегионального неравенства по названному показателю не претерпел статистически значимых изменений.

Методология

Мы использовали валовой региональный продукт по субъектам Российской Федерации (валовая добавленная стоимость в текущих базисных ценах) за период с 2005 по 2020 годы; данные о ВРП взяты с официального сайта Федеральной службы государственной статистики РФ [7].

Из-за отсутствия надлежащих данных за 2005 и 2010 годы мы исключили из анализа Ненецкий автономный округ и Архангельскую область без автономного округа (Северо-Западный федеральный округ), Крым и Севастополь (Южный федеральный округ), Ханты-Мансийский федеральный округ, Автономный округ – Югра, Ямало-Ненецкий автономный округ, Тюменскую область без автономных округов (Уральский федеральный округ).

Оба вида конвергенции (бета и сигма) могут подвергаться эмпирическому изучению. В случае бета-конвергенции натуральные логарифмы прироста выпуска в i регионах за период T времени регрессируются на натуральные логарифмы начальных значений выпуска в момент времени t. Начальная формулировка уравнения сходимости была представлена Р. Барро и К. Сала-и-Мартином [11; 12] с использованием подхода нелинейных наименьших квадратов (NLS) для оценки. Однако во многих случаях исследователи предпочитают линейное преобразование, что позволяет использовать методы оценки обычных наименьших квадратов (OLS), как показано в работах А. Дапена и др. [18], Г. Шмидта [26] и А. Янга и др. [28].

Зависимая переменная в уравнении сходимости может быть либо региональная скорость роста между двумя различными годами, либо среднегодовая скорость роста. Для определения статистической значимости проводятся тесты проверки гипотез, включающие t-тесты для коэффициентов регрессии и, в случае оценки методом наименьших квадратов, F-тесты для оценки значимости статистики R².

Основным параметром интереса в этой модели является β, отсюда и терминология «бета конвергенция» для описания моделируемого процесса. Когда β < 0 и имеет статистическую значимость, это означает существование абсолютной бета конвергенции. Когда в конвергентном уравнении учитываются дополнительные переменные, обычно называемые условными переменными, это превращается в тест на условную бета конвергенцию [29].

Альтернативная интерпретация коэффициента β может быть выявлена при рассмотрении скорости сходимости, обозначаемой как λ (lambda) и H (Halflife). Последнее представляет собой время, выраженное в рассматриваемых периодах времени, необходимое для уменьшения региональных различий вдвое.

Сигма конвергенция может быть оценена двумя различными подходами, в зависимости от количества рассматриваемых периодов времени. Вначале определяется степень регионального неравенства среди всех регионов в определенный момент времени, обозначаемая как σ_t, или коэффициент вариации, cv_t, для ВРП на душу населения в его исходной или натурально логарифмированной форме. При рассмотрении только двух конкретных лет вычисляется отношение этих параметров. Например, если σ_t1 > σ_t2, это означает снижение регионального неравенства с момента t₁ до t₂. Для проверки значимости может быть применен анализ дисперсии (analysis of variations, ANOVA), где статистика теста представляет собой отношение соответствующих дисперсий (σ₂), как разъясняется в работах Д. Фурчери [19], Г. Шмидта [26] и А. Янга и др. [28].

В контексте временны́х рядов параметр разброса регрессируется по времени и одновременно визуализируется. Отрицательный коэффициент наклона времени в этой регрессии свидетельствует о наличии сигма конвергенции, что продемонстрировано в работах Г. Гекке и М. Хютера [20], Я. Хуанга и Я. Люнга [21]

Более подробное описание данной методологии приводится в нашей предыдущей работе по данной тематике [4].

Результаты исследования

Ниже представлены результаты анализа конвергентных процессов в экономике регионов России в 2005-2020 г. Мы последовательно сравнивали бета и сигма конвергенцию в 2010, 2015 и 2020 годах с базовым периодом – 2005 г.

Мы использовали следующие обозначения в таблицах ниже:

Alpha, Beta – коэффициенты регрессии;

df1 – количество комбинаций уровней факторов;

df2 – количество наблюдений;

Estimate – оценка стандартного отклонения параметра;

F-value – вариация между средними выборками / вариация внутри выборок;

Halflife – количество лет до сокращения 50-процентного разрыва в уровне ВРП;

Lambda – скорость конвергенции;

NA – не применяется;

Non-linear Least Squares, NLS – метод нелинейных наименьших квадратов;

Ordinary Least Squares, OLS – метод наименьших квадратов;

p-value – вероятность того, что наблюдаемое различие могло произойти случайно (доказательство против нулевой гипотезы);

Quotient – частное отклонений;

R-Squared – a statistical measure that represents the proportion of the variance for a dependent variable that's explained by an independent variable or variables in a regression model;

Std. Error – стандартное отклонение выборочного распределения параметра;

t-value – отношение разницы между средним значением двух наборов выборок и вариацией, которая существует в наборах выборок;

Pr – значение p, связанное со значением t либо F.

В таблице 1 представлены результаты анализа бета конвергенции экономик регионов России в 2005-2010 гг. по методу наименьших квадратов.

Таблица 1. Абсолютная бета конвергенция. Регионы России, 2005-2010 гг.

Таблица 2 содержит данные о бета конвергенции экономик российских регионов в 2005-2010 гг., рассчитанные по методу нелинейных наименьших квадратов.

Таблица 2. Абсолютная бета конвергенция. Регионы России, 2005-2010 гг.

Мы визуализировали результаты анализа бета конвергенции экономического развития российских регионов (рис. 1).

Рисунок 1. Бета конвергенция регионов России, 2005 – 2010 гг.

Источник: Подготовлено авторами

В таблице 3 представлены результаты анализа сигма конвергенции в экономике российских регионов в исследуемый период.

Таблица 3. Сигма конвергенция. Регионы России, 2005-2010 гг.

Можно констатировать, что полученные результаты свидетельствуют о наличии бета конвергенции экономик российских регионов в 2005-2010 гг. Подтверждением нашего вывода является отрицательный наклон прямой на рис. 1, а также значения коэффициентов модели в таблицах 1-2 (α, β, F value; p-value < 0.05).

В тоже время, мы не обнаружили сигма конвергенции в исследуемый период.

Резюме: бета и сигма конвергенции в 2005-2010 гг.

Скорость гармонизации: 0,4% в год, срок преодоления 50% разрыва в уровне ВРП на душу населения между регионами: 156 лет (метод OLS).

Скорость гармонизации: 0,5% в год, срок преодоления 50% разрыва в уровне ВРП на душу населения между регионами: 147 лет (метод NLS).

Частное отклонений (в уровне ВРП на душу населения): 1,16.

В таблице 4 нами приведены результаты расчетов бета конвергенции по методу наименьших квадратов экономик регионов России в 2005-2015 гг.

Таблица 4. Абсолютная бета конвергенция. Регионы России, 2005-2015 гг.

Таблица 5 содержит коэффициенты модели бета конвергенции экономики российских регионов в названный период наблюдений, определенные по методу нелинейных наименьших квадратов.

Таблица 5. Абсолютная бета конвергенция. Регионы России, 2005-2015 гг.

На рисунке 2 мы представили график бета конвергенции в экономиках регионов России в 2005-2015 гг.

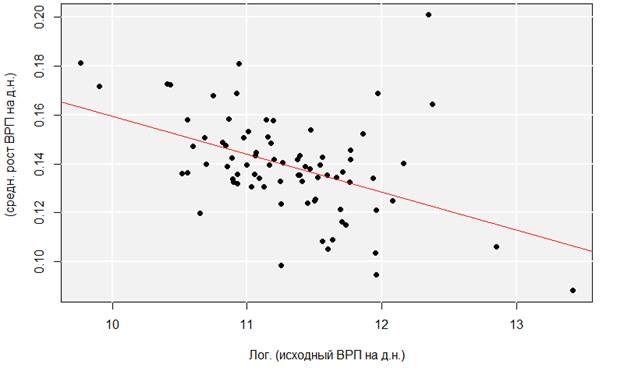
Рисунок 2. Бета конвергенция регионов России, 2005 – 2015 гг.

Источник: Подготовлено авторами

Результаты анализа сигма конвергенции экономик российских регионов приведены в таблице 6.

Таблица 6. Сигма конвергенция. Регионы России, 2005-2015 гг.

Как следует из таблиц 4-5, в экономиках российских регионов в 2005-2010 гг. наблюдается бета конвергенция. Этот вывод подтверждается отрицательным наклоном прямой на рис. 2, а также значениями коэффициентов модели в таблицах 4-5 (α, β, F value; p-value < 0.05).

Аналогично периоду с 2005 по 2010 гг., мы не обнаружили сигма конвергенции в 2005-2015 гг. Более того, мы наблюдаем увеличение частного отклонений в величине валового регионального продукта по сравнению с 2010 г., а также сроков преодоления 50% разрыва в величине ВРП российских регионов. Сроки гармонизации, напротив, уменьшились в сравнении с 2010 г.

Резюме: бета и сигма конвергенции в 2005-2015 гг.

Скорость гармонизации: 0,2% в год, срок преодоления 50% разрыва в уровне ВРП на душу населения между регионами: 444 года (метод OLS).

Скорость гармонизации: 0,2% в год, срок преодоления 50% разрыва в уровне ВРП на душу населения между регионами: 408 лет (метод NLS).

Частное отклонений (в уровне ВРП на душу населения): 1,25.

В таблице 7 мы представили коэффициенты модели бета конвергенции экономики регионов России ы 2005-2020 гг. (метод наименьших квадратов).

Таблица 7. Абсолютная бета конвергенция. Регионы России, 2005-2020 гг.

Значения коэффициентов модели бета конвергенции (метод нелинейных наименьших квадратов) в 2005-2020 гг. представлены в таблице 8.

Таблица 8. Абсолютная бета конвергенция. Регионы России, 2005-2020 гг.

Визуализация модели бета конвергенции (рис. 3) также демонстрирует отрицательный наклон прямой, что свидетельствует в пользу нашего предположения о наличии названного вида конвергенции в анализируемый период.

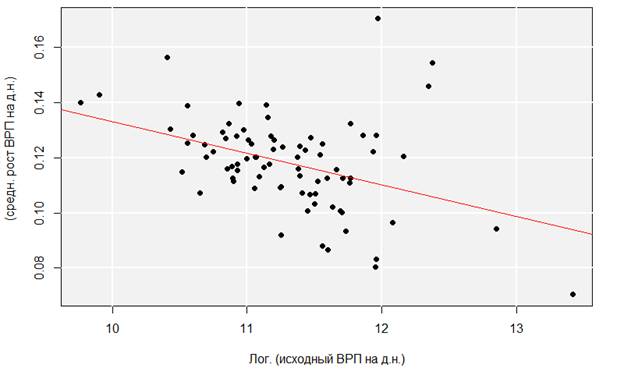
Рисунок 3. Бета конвергенция регионов России, 2005 – 2020 гг.

Источник: Подготовлено авторами

Коэффициенты модели сигма конвергенции для регионов России в 2005-2020 гг. представлены в таблице 9.

Таблица 9. Сигма конвергенция. Регионы России, 2005-2020 гг.

Как следует из таблиц 7-8, в экономиках российских регионов в 2005-2020 гг. наблюдается бета конвергенция. Этот вывод подтверждается отрицательным наклоном прямой на рис. 3, а также значениями коэффициентов модели в указанных выше таблицах (α, β, F value; p-value < 0.05).

Аналогично периоду 2005-2010 гг. и 2005-2015 гг., мы не обнаружили сигма конвергенции в 2005-2020 гг. Мы вновь вынуждены констатировать увеличение частного отклонений в величине валового регионального продукта по сравнению с 2010 и 2015 г.г., а также сроков преодоления 50% разрыва в величине ВРП российских регионов. Сроки гармонизации, напротив, уменьшились и в сравнении с 2010 г., и с 2015 г.

Резюме: бета и сигма конвергенции в 2005-2020 гг.

Скорость гармонизации: 0,08% в год, срок преодоления 50% разрыва в уровне ВРП на душу населения между регионами: 902 года (метод OLS).

Скорость гармонизации: 0,08% в год, срок преодоления 50% разрыва в уровне ВРП на душу населения между регионами: 822 года (метод NLS).

Частное отклонений (в уровне ВРП на душу населения): 1,26.

Заключение

Полученные нами результаты свидетельствуют о наличии бета конвергенции в экономике регионов России в анализируемый период, т.е. регионы с более низкими исходными условиями демонстрируют более высокие темпы роста ВРП, что согласуется с неоклассической теорией экономического роста. В то же время расчеты свидетельствуют об отсутствии убедительных статистических данных о сигма конвергенции экономик регионов России между 2005 и, соответственно, 2010, 2015 и 2020 годами. Разница величины коэффициента вариаций не является статистически значимой согласно полученному р-значению. Это говорит о том, что относительная изменчивость переменной за анализируемый период времени существенно не изменилась. В наблюдаемый период невозможно установить снижение регионального неравенства (по величине ВРП на душу населения) между регионами России, что является подтверждением нашей гипотезы.

На основе наших выводов можно сделать вывод о том, что низкие темпы конвергенции между российскими регионами наряду с отсутствием признаков сигма конвергенции предполагают наличие дивергентных процессов в экономике регионов России.