Анализ эволюции сближения экономического развития регионов России

Введение

Актуальность темы исследования

Дивергенция в экономическом развитии является серьезной проблемой для государства и общества, поскольку может привести к социальной и политической нестабильности, ухудшению состояния окружающей среды и другим негативным последствиям. Изучение причин и движущих сил дивергенции имеет важное значение для разработки эффективной политики и стратегий, направленных на содействие экономической конвергенции и устойчивому развитию.

В нашей предыдущей статье [3] мы представили результаты анализа конвергентных процессов экономического развития российских регионов по валовому региональному продукту на душу населения. Мы установили, что в развитии регионов России в 2015-2020 гг. присутствует бета конвергенция (регионы с низким уровнем ВРП на душу населения растут более высокими темпами, чем более богатые регионы), но отсутствует сигма конвергенция, т.е. региональное неравенство не уменьшается в течение исследуемого периода времени. В настоящей работе мы осуществили процедуру кластеризации в целях определения так называемых «клубов конвергенции» (кластеров), экономическое развитие которых сближается с течением времени, а также выявления регионов, где этот процесс отсутствует.

Литературный обзор

Исследователи, занимающиеся проблемами конвергенции, довольно рано пришли к мысли, что конвергенция является неоднородным процессом, и страны можно объединить в конвергентные кластеры («клубы»). Одним из первых [19] это заметил У. Баумоль, который, анализируя темпы роста валового внутреннего продукта на душу населения в 72 странах в период с 1950 по 1980 годы, высказал предположение о том, что среди них существует более одного клуба конвергенции [7, p. 1080]. Эта идея получила свое дальнейшее развитие во многих работах. Л. Коррадо, Р. Мартин и М. Уикс проверили наличие региональных кластеров конвергенции в Европейском союзе, используя методологию эндогенного отбора региональных кластеров с использованием многомерного теста на стационарность, где количество и состав кластеров определяются применением парных тестов региональных различий валового регионального продукта с течением времени [9]. В. Куфенко, К. Преттнер и В. Гелосо протестировали модель Р. Солоу в отношении межстранового неравенства на обширном историческом материале и установили, что до Великой промышленной революции наблюдался низкий уровень неравенства в доходах по странам (в период «мальтузианской стагнации»), после чего резко возросло неравенство в доходах между странами (период «Великой дивергенции») и, наконец, наблюдается снижение неравенства доходов по странам до уровня, превышающего уровень, существовавший до промышленной революции (период «Клубной конвергенции») [11]. Ц.-Л. Сяо, Ю. Ванг и В.-Ц. Жу установили пространственное расхождение между клубами конвергенции по валовому внутреннему продукту и уровнем ночной освещенности провинций Китая, а также в отношении темпов роста названных клубов конвергенции [21]. Ц. Пан, Ц. Лю и Ц. Пенг использовали методы цепи Маркова и пространственной цепи Маркова и определили, с 1999 года региональная энергоэффективность в Китае характеризуется «клубной конвергенцией», а переход к энергоэффективности в Китае тесно связан с региональными особенностями [13]. Этот эмпирический анализ предоставил названным авторам пространственное объяснение «клубам конвергенции» региональной энергоэффективности в Китае. М. Херрериас и К. Ордонез, исходя из гипотезы о существовании клубной или кластерной конвергенции высказывают предположение о том, доход на душу населения в регионе приближается к долгосрочной траектории роста, которая зависит от основных структурных характеристик региона, а также от того, превышает ли его первоначальный доход на душу населения конкретную пороговую величину ВВП или ниже нее. Регионы, которые начинают с превышения порогового значения, будут сходиться к более высокому стабильному состоянию ВВП, образуя кластеры, а те, которые начинаются ниже порогового уровня, будут сходиться к более низкому стабильному состоянию ВВП [10, pp. 156-157]. К. Ринц и Д. Вурхейс не используют понятие «клубов», однако производят разбиение распределения доходов в США по процентилям, диагностируя дивергенцию среди групп населения по названному показателю [16]. Д. Бернетт исследует клубы конвергенции по выбросам CO2 в штатах США в период с 1960 по 2010 гг., применяя эндогенную группировку и регрессионный тест конвергенции и приходит к выводу, что в 26 штатах наблюдается конвергенция, тогда как в остальных наличествуют дивергентные процессы [8].

Научный пробел

В отечественной экономической литературе тема региональной конвергенции / дивергенции представлена небольшим количеством исследований, например работами таких авторов, как Н. Амирова, О. Балаш, Е. Звягина, Т. Юрченко, А. Полбин, Т. Ивахненко [1; 2; 4; 5]. Анализ клубов конвергенции экономического развития регионов России осуществлен лишь в упомянутой выше работе Э. Таймаза [18], однако в ней не упоминаются регионы, не входящие ни в один из клубов и представляющие дивергентную группу; кроме того, указанный автор обнаружил меньшее количество клубов конвергенции среди российских регионов по сравнению с нашим исследованием. Наше исследование призвано заполнить существующий пробел.

Цель исследования

Цель нашего исследования – диагностировать наличие клубов конвергенции экономического развития российских регионов по уровню валового регионального продукта на душу населения и определить группу субъектов Российской Федерации, в которых наблюдается дивергентное развитие в анализируемый период времени (2015-2020 гг.).

Научная новизна

Научная новизна настоящего исследования заключается в установлении процесса дивергентного экономического развития среди регионов России наряду с определением наличия клубов конвергенции субъектов Российской Федерации.

Авторская гипотеза

Гипотеза авторов состоит в том, что гетерогенность экономического пространства России находит свое проявление через наличие нескольких клубов конвергенции, а также группы регионов, в которой наблюдается дивергентное экономического развития.

Методология

Для своего исследования мы воспользовались официальными статистическими данными о величине валового регионального продукта на душу населения с 2015 по 2020 год, представленные на сайте Федеральной службы государственной статистики России [6].

Диагностику наличия клубов конвергенции экономического развития регионов России мы проводили с использованием процедур кластеризации по методу П. Филлипса и Д. Сула [14; 15], К. фон Линкера и Р. Теннессена [20].

Процедура кластеризации П. Филлипса и Д. Сула

Процедура кластеризации П. Филлипса и Д. Сула – это статистический метод, используемый для выявления групп экономик, которые сходятся к общему уровню экономического развития. Подход, предложенный П. Филлипсом и Д. Сулом, основан на декомпозиции панельных данных по интересующей переменной [17, pp. 142-143]. Нулевая гипотеза сходимости проверяется с помощью одностороннего t-теста, устойчивого к гетероскедастичности и автокорреляции неравенства. Эта процедура, как правило, называется log t-test.

Процедура кластеризации П. Филлипса и Д. Сула используется для группировки экономик в кластеры на основе сходства их факторных нагрузок [15]. Факторные нагрузки – это коэффициенты, которые указывают, насколько каждая экономика подвержена влиянию каждой из общих тенденций. Экономики с похожими факторными нагрузками считаются сближающимися (конвергирующими) к общему уровню развития.

Модель К. фон Линкера и Р. Теннессена

Модель К. фон Линкера и Р. Теннессена – это еще один статистический метод для выявления клубов конвергенции. Модель основана на идее о том, что экономики, сближающиеся к общему уровню развития, должны иметь схожие модели сходимости и дисперсии своих экономических показателей. Сходимость относится к тенденции экономик с первоначально более низкими уровнями развития догонять экономики с первоначально более высокими уровнями развития. Дисперсия относится к разбросу экономических показателей по экономикам в выборке [20].

К. фон Линкер и Р. Теннессен предложили два новшества в алгоритме слияния П. Филлипса и Д. Сула, добавив дополнительное условие к клубной кластеризации, что позволяет избежать ошибок при слиянии процедур в случае перехода из клуба в клуб. К. фон Линкер и Р. Теннессен также утверждают, что единицы, идентифицированные как расходящиеся по первоначальной процедуре кластеризации П. Филлипа и Д. Сула, не обязательно все еще расходятся в случае новых клубов конвергенции, выявленных с помощью алгоритма слияния клубов [17, p. 145].

Модель К. фон Линкера и Р. Теннессена используется для выявления клубов конвергенции на основе сходства параметров сходимости и дисперсии экономик. Экономики с похожими параметрами сходимости и дисперсии считаются сближающимися к общему уровню развития.

Сравнение двух методов

Процедура кластеризации П. Филлипса и Д. Сула является непараметрическим методом, что означает, что она не делает предположений о распределении данных. Это делает процедуру более устойчивой к выбросам и другим видам нерегулярностей данных. Однако названная процедура менее эффективна, чем модель К. фон Линкера и Р. Теннессена.

Модель К. фон Линкера и Р. Теннессена является параметрическим методом, что означает, что она делает некоторые предположения о распределении данных. Это делает процедуру менее устойчивой к выбросам и другим видам нерегулярностей данных. Однако процедура более эффективна, чем процедура кластеризации П. Филлипса и Д. Сула.

В целом, процедура кластеризации П. Филлипса и Д. Сула является хорошим выбором для исследовательского анализа данных, в то время как модель К. фон Линкера и Р. Теннессена является хорошим выбором для более строгой проверки гипотез конвергенции. В своем исследовании мы использовали оба подхода.

Результаты исследования

Нами установлено, что регионы России по показателю валового регионального продукта на душу населения в период с 2015 по 2020 год можно объединить в 9 клубов конвергенции, состоящих из 80 регионов; пять регионов входят в дивергентную группу. Ключевые статистические характеристики конвергентных клубов приведены в таблице 1:

Таблица 1. Статистические показатели клубов конвергенции регионов России по уровню ВРП на душу населения в 2005-2020 гг.

Источник: Подготовлено авторами.

Примечание: beta – коэффициент линейной регрессии, который измеряет степень взаимосвязи между независимой и зависимой переменными; std.err. – стандартное отклонение выборочного распределения параметра; t-value – отношение разницы между средним значением двух наборов выборок и вариацией, которая существует в наборах выборок; p-value – вероятность того, что наблюдаемое различие могло произойти случайно (доказательство против нулевой гипотезы).

На рисунке 1 представлена карта Российской Федерации, на которой выделены клубы конвергенции регионального экономического развития.

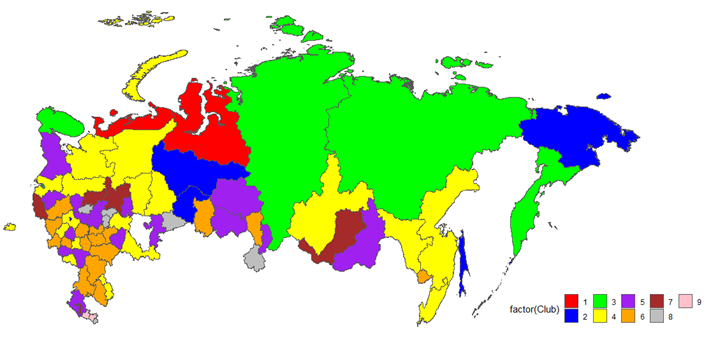
Рисунок 1. Клубы конвергенции экономического развития российских регионов в 2015-2020 гг. по уровню валового регионального продукта на душу населения.

Источник: Подготовлено авторами.

Рассмотрим каждый из клубов конвергенции отдельно. Нами использованы следующие статистические показатели:

- beta – это коэффициент линейной регрессии, который измеряет степень взаимосвязи между независимой и зависимой переменными;

- std. err. (standard error) – стандартное отклонение выборочного распределения параметра;

- t-value – отношение разницы между средним значением двух наборов выборок и вариацией, которая существует в наборах выборок;

- p-value – вероятность того, что наблюдаемое различие могло произойти случайно (доказательство против нулевой гипотезы).

Клуб 1: Ненецкий автономный округ, Ямало-Ненецкий автономный округ.

Показатели:

- beta: 4.1224. Коэффициент бета 4.1224 указывает на положительную связь между анализируемыми переменными.

- std. err: 3.3557. Значение стандартной ошибки 3,3557 указывает на то, что оценка бета-коэффициента не является очень точной. Истинное значение бета-коэффициента может находиться в пределах от -2,0799 - 3,3557 = -5,4356 до -2,0799 + 3,3557 = 1,2768.

- t-value: 1.2285. В нашем случае t-значение относительно невелико, что предполагает, что предполагаемая связь не сильно отличается от нуля.

- p-value: 0.8904. P-значение, связанное с t-значением, равно 0.8904. P-значение 0.8904 довольно высокое, что указывает на отсутствие веских оснований для отклонения нулевой гипотезы о том, что коэффициент равен нулю. Другими словами, предполагаемая взаимосвязь не является статистически значимой.

Клуб 2: Чукотский автономный округ, Сахалинская область, Магаданская область, Ханты-Мансийский автономный округ – Югра, Тюменская область, Москва.

Показатели:

- beta: 0.2764. Коэффициент бета 0.2764 указывает на положительную связь между анализируемыми переменными, однако величина этого эффекта относительно мала.

- std. err: 0.6893. Значение стандартной ошибки 0,6893 указывает на то, что оценка бета-коэффициента является достаточно точной и может находиться в пределах от -0,5 - 0,6893 = -1,1893 до -0,5 + 0,6893 = -0,0107.

- t-value: 0.401. В данном случае t-значение относительно невелико, что предполагает, что предполагаемая взаимосвязь не сильно отличается от нуля.

- p-value: 0.6558. P-значение 0.6558 довольно высокое, что указывает на отсутствие веских оснований для отклонения нулевой гипотезы о том, что коэффициент равен нулю.

Клуб 3: Республика Саха (Якутия), Мурманская область, Санкт-Петербург, Красноярский край, Камчатский край.

Показатели:

- beta: -0.0005. В данном случае бета -0.0005 указывает на очень слабую отрицательную связь между анализируемыми переменными.

- std. err: 0.8496. Стандартная ошибка 0,8496 означает, что существует вероятность того, что истинное значение бета-коэффициента может находиться в пределах от -0,5 - 0,8496 = -1,3496 до -0,5 + 0,8496 = -0,1504.

- t-value: -0.0006. В данном случае t-значение -0.0006 очень близко к нулю, что указывает на то, что оцененная бета не отличается статистически значимо от нуля.

- p-value: 0.4997. В данном случае p-значение 0.4997 относительно высоко, что говорит об отсутствии веских оснований для отклонения нулевой гипотезы (которая утверждает, что коэффициент равен нулю).

Клуб 4: Республика Коми, Архангельская область, Московская область, Республика Татарстан, Ленинградская область, Хабаровский край, Белгородская область, Иркутская область, Свердловская область, Приморский край, Амурская область, Калужская область, Липецкая область, Вологодская область, Пермский край, Оренбургская область, Калининградская область, Астраханская область.

Показатели:

- beta: -0.9436. Бета-коэффициент -0.9436 указывает на отрицательную связь между анализируемыми переменными.

- std. err: 0.5726. Стандартная ошибка 0,5726 означает, что существует вероятность того, что истинное значение бета-коэффициента может находиться в пределах от -0,5 - 0,5726 = -1,0726 до -0,5 + 0,5726 = -0,0274.

- t-value: -1.6481. В этом случае t-значение отрицательное, что отражает отрицательную связь между переменными.

- p-value: 0.0497. P-значение 0.0497 меньше общепринятого уровня значимости 0.05. Это предполагает, что есть основания отвергнуть нулевую гипотезу о том, что коэффициент равен нулю, что указывает на то, что предполагаемая взаимосвязь статистически значима.

Клуб 5: Республика Карелия, Томская область, Самарская область, Республика Хакасия, Нижегородская область, Ярославская область, Курская область, Тульская область, Новосибирская область, Новгородская область, Челябинская область, Воронежская область, Краснодарский край, Удмуртская Республика, Владимирская область, Забайкальский край.

Показатели:

- beta: -0.3388. Бета-коэффициент -0,3388 указывает на отрицательную связь между анализируемыми переменными.

- std. err: 0.6346. Стандартная ошибка 0,6346 означает, что истинное значение бета-коэффициента может находиться в пределах от -0,5 - 0,6346 = -1,1346 до -0,5 + 0,6346 = -0,0654.

- t-value: -0.5338. В этом случае t-значение отрицательное, отражая отрицательную связь между переменными. Однако t-значение относительно близко к нулю, что указывает на то, что предполагаемая взаимосвязь не сильно отличается от нуля.

- p-value: 0.2967. P-значение 0,2967 выше общепринятого уровня значимости 0,05. Это предполагает, что нет веских оснований отвергать нулевую гипотезу о том, что коэффициент равен нулю, что указывает на то, что предполагаемая взаимосвязь не является статистически значимой.

Клуб 6: Республика Башкортостан, Рязанская область, Ростовская область, Еврейская автономная область, Омская область, Волгоградская область, Кемеровская область, Тверская область, Орловская область, Смоленская область, Пензенская область, Тамбовская область, Ульяновская область, Саратовская область, Брянская область, Республика Калмыкия, Республика Мордовия.

Показатели:

- beta: 0.0023. Коэффициент бета 0.0023 указывает на очень слабую положительную связь между анализируемыми переменными.

- std. err: 0.2966. Значение стандартной ошибки 0.2966 указывает на то, что оценка бета-коэффициента является достаточно точной. Стандартная ошибка 0.2966 означает, что существует вероятность того, что истинное значение бета-коэффициента может находиться в пределах от -0.5 - 0.2966 = -0.7966 до -0.5 + 0.2966 = -0.2034.

- t-value: 0.0076. этом случае t-значение чрезвычайно близко к нулю, что указывает на то, что предполагаемая взаимосвязь не сильно отличается от нуля.

- p-value: 0.503. P-значение 0.503 значительно выше общепринятого уровня значимости 0.05. Это предполагает, что нет веских оснований отвергать нулевую гипотезу о том, что коэффициент равен нулю.

Клуб 7: Псковская область, Костромская область, Кировская область, Республика Адыгея, Республика Бурятия.

Показатели:

- beta: 0.0193. Коэффициент бета 0,0193 указывает на очень слабую положительную связь между анализируемыми переменными.

- std. err: 1.0259. Значение стандартной ошибки 1.0259 указывает на то, что оценка бета-коэффициента является достаточно точной. Истинное значение бета-коэффициента находится в пределах от -0.5 - 1.0259 = -2.0259 до -0.5 + 1.0259 = 0.5241. Таким образом, стандартная ошибка 1.0259 указывает на то, что существует относительно небольшая вариативность в предполагаемой взаимосвязи между двумя переменными.

- t-value: 0.0188. этом случае t-значение очень близко к нулю, что указывает на то, что предполагаемая взаимосвязь не сильно отличается от нуля.

- p-value: 0.5075. P-значение 0,5075 существенно выше общепринятого уровня значимости 0,05. Это предполагает, что нет веских оснований отвергать нулевую гипотезу о том, что коэффициент равен нулю, что указывает на то, что предполагаемая взаимосвязь не является статистически значимой.

Клуб 8: Севастополь, Курганская область, Алтайский край, Республика Марий Эл, Чувашская республика, Республика Алтай, Ивановская область, Крым, Республика Северная Осетия – Алания.

Показатели:

- beta: -0.004. Бета-коэффициент -0.004 указывает на очень слабую отрицательную связь между анализируемыми переменными.

- std. err: 1.2333. Значение стандартной ошибки 1.2333 указывает на то, что оценка бета-коэффициента является достаточно точной. Истинное значение бета-коэффициента находится в пределах одного стандартного отклонения от оцененного значения, т.е. в пределах от -0.5 - 1.2333 = -2.7333 до -0.5 + 1.2333 = 0.7333. Таким образом, стандартная ошибка 1.2333 указывает на то, что существует относительно небольшая вариативность в предполагаемой взаимосвязи между двумя переменными.

- t-value: -0.0032. В этом случае t-значение чрезвычайно близко к нулю, что указывает на то, что предполагаемая взаимосвязь не сильно отличается от нуля.

- p-value: 0.4987. P-значение 0.4987 значительно выше общепринятого уровня значимости 0.05. Это предполагает, что нет веских оснований отвергать нулевую гипотезу о том, что коэффициент равен нулю, что указывает на то, что предполагаемая взаимосвязь не является статистически значимой.

Клуб 9: Кабардино-Балкарская республика, Карачаево-Черкесская республика.

Показатели:

- beta: -2.0799. Коэффициент бета -2,0799 указывает на отрицательную связь между анализируемыми переменными.

- std. err: 1.6086. Значение стандартной ошибки 1.6086 указывает на то, что оценка бета-коэффициента является достаточно точной. Стандартная ошибка 1.6086 означает, что существует вероятность того, что истинное значение бета-коэффициента находится в пределах одного стандартного отклонения от оцененного значения, т.е. в пределах от -0.5 - 1.6086 = -3.1086 до -0.5 + 1.6086 = 1.1086.

- t-value: -1.293. В этом случае t-значение отрицательное, отражая отрицательную связь между переменными. Однако t-значение относительно близко к нулю, что указывает на то, что предполагаемая взаимосвязь не сильно отличается от нуля.

- p-value: 0.098. P-значение 0,098 несколько выше общепринятого уровня значимости 0,05. Это предполагает, что есть основания отвергнуть нулевую гипотезу о том, что коэффициент равен нулю, что указывает на то, что предполагаемая взаимосвязь может быть статистически значимой на уровне значимости, чуть ниже 0,05.

Дивергентные регионы: Ставропольский край, Республика Тыва, Республика Дагестан, Чеченская республика, Республика Ингушетия.

На рисунке 2 мы представили средние переходные траектории (‘Average transition paths’) всех девяти клубов конвергенции в течение анализируемого периода времени (2015-2020 годы):

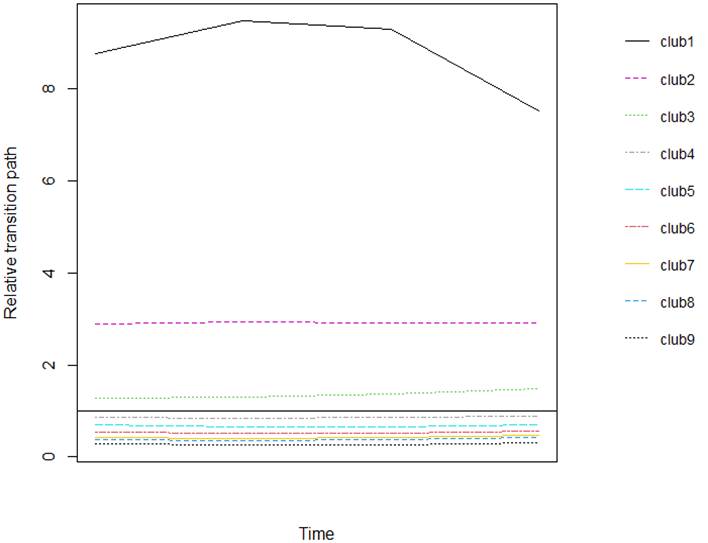
Рисунок 2. Средние переходные траектории конвергентных процессов в клубах конвергенции регионов России в 2015-2020 гг.

Источник: Подготовлено авторами.

Относительные переходные траектории, представленные на рисунке 2, позволяют высказать предположение, что 9 клубов конвергенции можно объединить в 4, оставив 1, 2 и 3 клуб отдельно, а клубы с 4 по 9 включить в один. В результате мы получим то же количество клубов, как и в исследовании Э. Таймаза [18]. Однако регионы, входящие в клубы конвергенции у названного автора, не совпадают с теми, что получены нами. Кроме того, мы использовали статистические данные за разные периоды времени.

Тем не менее, если мы объединяем клубы с 4 по 9 в один клуб конвергенции, то мы можем их рассматривать в качестве субконвергентных клубов, наличие которых по мнению П. Филлипса и Д. Сула делает затруднительным процесс конвергенции [14]. Этот вывод согласуется с результатами нашего исследования [3], в котором мы установили усиление дивергентных процессов в экономике российских регионов после 2005 года. Как показали Н. Пальма и Д. Рейс, смена конвергентных процессов дивергентными в экономике страны является распространенным феноменом [12].

Заключение

Полученные нами результаты показывают, что связь между двумя переменными в клубах 1 и 4 является сильной. При увеличении значения одной переменной на одну единицу значение другой переменной увеличивается на 4.122 и -0.944 единицы соответственно.

Связь между двумя переменными в клубах 2, 5, 6, 7 и 8 является слабой. При увеличении значения одной переменной на одну единицу значение другой переменной может увеличиваться или уменьшаться на небольшое значение.

Связь между двумя переменными в клубе 3 является практически нулевой. При увеличении значения одной переменной на одну единицу значение другой переменной не меняется.

Связь между двумя переменными в клубе 9 является умеренной. При увеличении значения одной переменной на одну единицу значение другой переменной может увеличиваться или уменьшаться на значительное значение.

Связь между двумя переменными в клубах 1 и 4 является статистически значимой. Связь между двумя переменными в клубах 2, 5, 6, 7 и 8 является статистически незначимой.

Связь между двумя переменными в клубе 4 является статистически значимой и достоверной. Связь между двумя переменными в клубе 9 является статистически значимой, но не является достоверной.

По нашему мнению, наличие довольно значительного количества клубов конвергенции среди российских регионов, крайне низкие темпы гармонизации регионального развития и большой срок преодоления 50-процентной разницы в уровне ВРП на душу населения, что было установлено нами в нашей предыдущей статье [3], а также выделение дивергентной группы регионов свидетельствуют о наличии дивергентных процессов в развитии экономики регионов России.

Это подтверждает нашу гипотезу, а также гипотезу П. Филипса и Д. Сула [14], которые показали невозможность конвергенции в условиях нескольких субконвергентных клубов.