Модифицированные функции предложения труда: классический и альтернативные варианты

Введение

Констатация недостатка занятых стала общим местом при анализе сегодняшнего положения в экономике России. Ситуация усугубилась в 2022 г. в связи с серьезным оттоком трудоспособного населения из страны. Привлечение работников из ближнего зарубежья, во-первых, не решает проблемы, а во-вторых, характеризуется нежелательными побочными эффектами. Между тем в России имеется значительный потенциал рабочей силы – трудоспособного населения, не предлагающего своих услуг на рынке труда. Использование в той или иной степени этого потенциала в народном хозяйстве должно способствовать преодолению спада в экономике. В силу этих обстоятельств изучение предложения на российском рынке труда представляется вполне своевременным.

В настоящей статье объединены результаты исследований, проведенных в двух направлениях: посвященные определению функций предложения труда на макроуровне и связанные с нестандартным подходом к построению уравнений регрессии.

При анализе рынка труда на макроуровне отсутствует возможность оперировать рядами наблюдений, относящимися к одному моменту времени. В силу этого обстоятельства проблему определения функции предложения труда (как и спроса на труд) следует решать на основе динамических рядов показателей, характеризующих рынок труда. Решению данной задачи посвящены публикации Винокурова Е.Ф. и Винокуровой Н.А. [1] (Vinokurov, Vinokurova, 2021) и [6] (Vinokurov, 2022). Изложенный в названных работах результат был использован в работе Винокурова Е.Ф. [5] (Vinokurov, 2022) при изучении вопроса о связи динамики заработной платы с уровнем безработицы.

В статье Винокурова Е.Ф. и Винокуровой Н.А. [1] (Vinokurov, Vinokurova, 2021) было показано, что функцию вида

y=f(W), (1)

где W – средняя реальная заработная плата, а y – уровень экономической активности населения, можно трактовать как модифицированную функцию предложения труда. Действительно, значение функции (1) представляет собой количество труда, предлагаемое в течение года при определенной заработной плате усредненным представителем рассматриваемой группы населения, выраженное в доле человеко-года. О различных вариантах построения данной функции и пойдет речь в настоящей статье.

Примененная в работе нестандартная методика определения модифицированных функций предложения труда представляет собой развитие идеи, высказанной в статье Винокурова Е.Ф. [3] (Vinokurov, 2017). В названной публикации указывалось на отсутствие логики в традиционном использовании при построении уравнений регрессии (и при выборе показателей колеблемости переменных) квадратов отклонений фактических значений признака от теоретических. Именно на основе этих величин определяются параметры уравнения регрессии при применении метода наименьших квадратов, а также более современных методов, в частности двойного метода наименьших квадратов и метода максимального правдоподобия. При этом получается, что «…изучая некоторое явление, ученые и прикладники, экономисты и медики, инженеры и агрономы, химики и палеонтологи оперируют не естественными для рассматриваемых объектов единицами измерения – рублями, штуками, тоннами, киловаттами или кубометрами, – а рублями, штуками, тоннами, киловаттами и кубометрами,… возведенными во вторую степень» [3, с. 58] (Vinokurov, 2017, р. 58).

Гораздо более логичным представляется опираться при определении вида и параметров уравнений регрессии на абсолютные значения разности между фактическими и теоретическими значениями переменных. Приведем еще цитату: «Математики предпочли квадратическое отклонение абсолютному не по недомыслию и не от хорошей жизни. Просто дело в том, что с абсолютными значениями величин математика плохо справляется» [3, с. 58] (Vinokurov, 2017, р. 58). Занятно, как неубедительно некоторые специалисты по математической статистике пытались объяснить, чем хороши возведенные в квадрат показатели. В одном из учебников можно прочитать, что при использовании среднего линейного отклонения «…нарушается элементарное правило математики, так как отклонения от среднего значения признака складываются без учета знаков… Отмеченный выше недостаток показателя среднего линейного отклонения может быть устранен путем возведения в квадрат отклонения вариантов от средней арифметической» [7, с. 178] (Kapelyushnikov, Oshchepkov, 2014, р. 178).

С появлением электронно-вычислительной техники ситуация принципиально изменилась. Компьютеры обеспечили возможность решать ранее неразрешимые или почти неразрешимые задачи, в том числе оперируя модулями значений тех или иных показателей. В частности, стало возможным использовать при построении уравнений регрессии не квадраты отклонений теоретических значений результирующего признака от наблюдаемых, а абсолютные значения этих отклонений. Именно этот подход к проблеме рассматривается в настоящей статье.

Модули вместо квадратов

Первая мысль, которая приходит в голову, – заменить критерий, определяющий значения параметров уравнения регрессии, с минимума суммы квадратов названных выше отклонений на минимум суммы модулей данных отклонений. Формализуем это положение.

Введем обозначения:

m – число факторов;

n – число наблюдений для каждого фактора;

х_ij – значение i-го наблюдения для j-го фактора;

у_i – наблюдаемое значение результирующего признака;

– теоретическое значение результирующего признака.

Пусть задан вид функции, связывающей значения результирующего признака со значениями факторов:

х_i1, х_i2, …, х_im), i=1, 2, …, n _. (2)

Положим, число параметров функции F равно р (р≥m).

При классическом подходе, когда используется метод наименьших квадратов, значения параметров функции F определяются исходя из критерия:

- )²→min. (3)

Предлагается заменить критерий (3) на условие

(4)

Однако представляется, что имеют право на существование и еще по крайней мере два критерия, определяющие выбор параметров уравнения регрессии. Такими критериями, по нашему мнению, являются, во-первых, минимум максимального модуля отклонений теоретических значений зависимой переменной от наблюдаемых и, во-вторых, минимум модуля максимального относительного (к наблюдаемому значению) отклонения. Формально эти критерии, соответственно, запишутся как:

max (5)

и

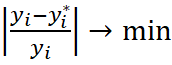max . (6)

Правда, критерий (6) может рассматриваться только в том случае, когда все значения не равны нулю.

Алгоритм выбора оптимального набора значений параметров искомых уравнений регрессии весьма прост и обеспечивает одновременное решение задачи при критериях (4), (5) и (6). Этот алгоритм включает в себя три этапа.

На первом этапе для каждого из р параметров задаются минимальное и максимальное значения – интервал, в пределах которого, как предполагаетcя, могут лежать значения данного параметра. Выбор этого интервала – задача, определяемая видом функции и совокупностью исходных данных (значениями х_ij и у_i).

На втором этапе выбирается для каждого параметра шаг, с которым должна при расчетах меняться величина этого параметра от нижней до верхней границы. Здесь выбор определяется точностью решения, которой может и хочет добиться исследователь. Интервал рассматриваемых значений и величина шага определяют число используемых при дальнейших расчетах вариантов значений каждого j-го параметра – q_j.

Третий этап – собственно расчеты. Они сводятся к определению при каждой из возможных комбинаций значений параметров и соответствующих суммы модулей отклонений ( ), а также максимальных по i значений модулей отклонений (max ) и относительных отклонений (max 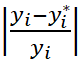). То есть речь идет о простом переборе. Число рассматриваемых комбинаций параметров уравнений регрессии – Q – рассчитывается по формуле:

Q= .

Комбинации значений параметров, при которых оказываются минимальными перечисленные величины, определят функции , обеспечивающие оптимум, определяемый критериями соответственно (4), (5) и (6).

После того как функции построены, встают два вопроса: об оценке качества построенных регрессионных моделей и о значимости полученных уравнений регрессии в целом и отдельных их параметров.

Если речь идет о парной линейной регрессии, то можно, конечно, в качестве показателя, отражающего меру качества регрессионной модели, воспользоваться коэффициентом детерминации, формула расчета которого приведена в любом учебнике статистики. Но… этот коэффициент базируется на понятии дисперсии, а значит, на не имеющих ни физического, ни экономического, ни какого-либо другого, кроме абстрактно-математического, смысла возведенных в квадрат величинах.

В качестве альтернативы коэффициенту детерминации для оценки качества уравнений регрессии можно предложить, как нам представляется, выраженное в процентах отношение суммы модулей отклонений к сумме модулей наблюдаемых значений результирующей переменной:

α=100 .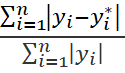

Этот показатель можно назвать индексом отклонений. Значение α при совпадении наблюдаемых и теоретических значений результирующей переменной для всех i равно нулю и возрастает по мере снижения качества модели. Для того чтобы сказать, какие значения α позволяют считать оцениваемую модель достаточно адекватной, необходимо накопить опыт расчета этого показателя для достаточно большого количества разнообразных уравнений регрессии. Пока такого опыта нет.

В качестве дополнительной к α характеристики качества модели можно (если все значения ненулевые) использовать выраженное в процентах максимальное относительное отклонение γ:

γ= 100 max .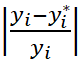

Этот показатель, как и индекс отклонений, равен нулю при совпадении наблюдаемых и теоретических значений результирующей переменной для всех i. Чем больше максимальное относительное расхождение этих значений, тем больше значение γ.

Для оценки значимости уравнений регрессии и их параметров, в принципе, ничто не мешает воспользоваться, соответственно, F-критерием Фишера и t-распределением Стьюдента, традиционно используемыми при статистических исследованиях. Правда, классический подход к проблеме, «как посмотришь с холодным вниманьем вокруг», вряд ли можно признать абсолютно объективным и обеспечивающим абсолютную точность. Но эта проблема лежит за пределами темы настоящей статьи.

Изложенная методика построения уравнений регрессии была апробирована на примере модифицированных функций предложения труда в Российской Федерации. Перейдем к описанию проделанной работы.

Модифицированные функции предложения труда в различных вариантах

Объектом рассматриваемого исследования является рынок труда России. Информационной базой для расчетов являются официальные данные Росстата, относящиеся к заработной плате и рабочей силе. То есть речь идет о «белом», отражаемом государственной статистикой рынке труда.

Целью работы было построение модифицированных функций предложения труда на макруровне, т.е. функций вида (1) с использованием представленной в предыдущем разделе настоящей статьи методики.

До 2017 г. численность экономически активного населения (она же численность рабочей силы) рассчитывалась отечественными статистическими органами как сумма занятых и безработных в возрасте от 15 до 72 лет. Затем по рекомендации Международной организации труда в рабочую силу стали включать занятых и более старших возрастов. В результате представляемые официальной статистикой значения показателей уровня экономической активности населения (он же уровень участия в рабочей силе) начиная с 2017 г. стали несопоставимыми с показателями за более ранний период. Тут уместно напомнить, что уровень экономической активности населения – это частное от деления численности рабочей силы на численность возрастной когорты населения, формирующей рабочую силу. Именно отказ от верхней границы возраста для лиц, входящих в рабочую силу, и сделал значения уровней экономической активности до и после 2017 г. несопоставимыми. Указанное обстоятельство определило то, что информационной базой настоящего исследования стала статистика, относящаяся к периоду до 2017 г.

На экономическую активность населения оказывает влияние множество факторов. Эти факторы можно подразделить на демографические, социально-экономические и институциональные. Довольно подробно эти факторы рассмотрены в работах Винокурова Е.Ф. и Винокуровой Н.А. [4] (Vinokurov, 2021) и [1] (Vinokurov, Vinokurova, 2021). Посвящены анализу экономической активности и публикации Винокурова Е.Ф. [6] (Vinokurov, 2022), Подольной Н.Н. [12]. «Российский рынок труда…» [13] (Podolnaya, 2015). Нередко в интернете размещаются аналитические материалы, относящиеся к данной теме, в частности Ляшека В. [8] (Kozlov, Erlikh, Dolgushevskiy, Polushin, 1975), (Фейнбера А. [15], «Уровень экономической активности…» [14], «Labour market outcomes…» [16], «О рынке труда…» [11] (Migranova, 2018). Разнообразные факторы влияют на уровень экономической активности разнонаправленно и в разной степени. Но нас, естественно, интересует наиболее существенный из них – заработная плата. Динамику именно этого показателя мы и будем сравнивать с динамикой уровня участия в рабочей силе.

Изменения уровня экономической активности населения России во времени графически отражены гистограммой на рисунке 1.

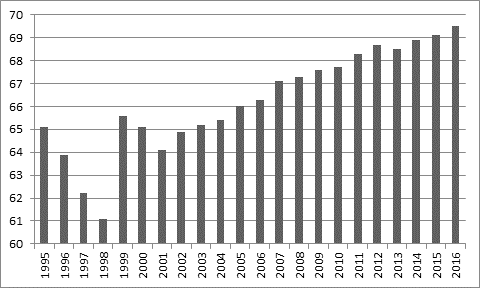
Рисунок 1. Динамика уровня экономической активности населения России (%)

Источник: составлено автором по материалам сборников «Труд и занятость в России». М.: Росстат, 2003–2017.

Поскольку подразумевается, что заработная плата в настоящем исследовании рассматривается в динамике, естественно, оперировать следует реальными ее значениями.

Животрепещущей теме оплаты труда посвящено немало работ отечественных экономистов. Назовем здесь две статьи, близкие к кругу вопросов, затрагиваемых в нашей работе: это публикации Миграновой Л.А. [8] (Kozlov, Erlikh, Dolgushevskiy, Polushin, 1975) и [9] (Lyashek, 2019). Изменения во времени реальной начисленной среднемесячной заработной платы в России отражены в виде гистограммы на рисунке 2 (базовым является 2008 г.).

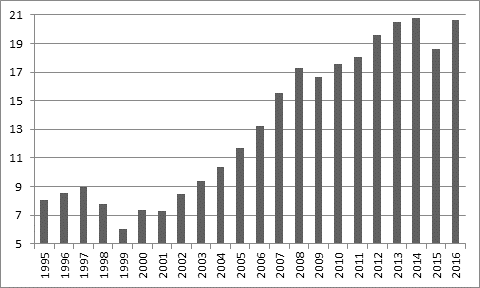
Рисунок 2. Динамика реальной среднемесячной начисленной заработной платы в России (тыс. руб.)

Источник: составлено автором по материалам сборников «Российский статистический ежегодник». М.: Росстат, 2002–2017.

Сопоставляя рисунки 1 и 2, можно сделать вывод: корреляция между уровнем экономической активности и зарплатой начинает очевидным образом просматриваться с 2000 года. Этот факт дал основание для положения, высказанного в работе Винокурова Е.Ф. [4] (Vinokurov, 2021): с 2000 года в России в сфере трудовых отношений начали действовать законы рынка. На этом основании в проводимых нами расчетах используется исходная информация начиная с 2000 г. Эта информация представлена в таблице 1.

Таблица 1

Исходная информация для расчета

модифицированных функций предложения труда

Как видно из приведенных выше данных, оба рассматриваемых показателя имели за рассматриваемый период очевидную тенденцию к росту, правда, непостоянному. Эта общая тенденция наглядно просматривается на поле корреляций, представленном на рисунке 3.

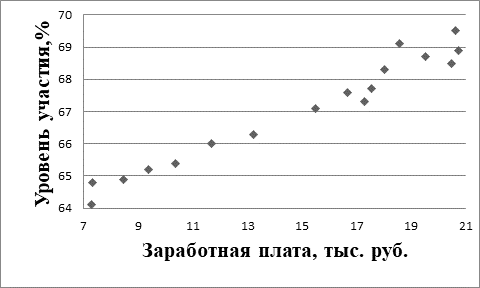
Рисунок 3. Поле корреляций для уровня экономической активности населения и реальной среднемесячной начисленной заработной платы

Источник: составлено автором.

Легко заметить, что темпы роста рассматриваемых показателей существенно отличаются. Наибольшая величина заработной платы (2014 г.) больше наименьшей (2001 г.) в 2,85 раза, а максимальное значение уровня экономической активности (2016 г.) больше наименьшего (2001 г.) всего на 8%. Однако на основе рисунка 3 можно достаточно уверенно сделать вывод о высокой корреляции между интересующими нас рядами данных и о линейном характере связи между ними. Последнее обстоятельство обусловило выбор линейной зависимости при построении модифицированных функций предложения труда в России начала ХХI века.

Это означает, что в наших расчетах в формуле (2) m=1, a p=2.

Итак, речь идет об определении параметров а и b функции вида:

y=aW+b. (7)

В дальнейших вычислениях уровень участия в рабочей силе у измеряется в процентах, а реальная заработная плата W – в тысячах рублей.

Расчеты мы начали с определения параметров функции (7) классическим путем – методом наименьших квадратов. Программа Excel выдала следующие значения параметров: а=0,344, b=61,90. Коэффициент детерминации для построенного регрессионного уравнения оказался равным 0,961.

Далее последовали расчеты трех вариантов уравнений регрессии вида (7), основанных на абсолютных значениях отклонений теоретических значений у от наблюдаемых.

Прежде всего, стояла проблема выбора границ интервалов, в пределах которых целесообразно было рассматривать возможные значения а и b, и величины шага, с которым должны были меняться эти параметры в ходе перебора их сочетаний с целью найти оптимальные из этих сочетаний, т.е. сочетания, соответствующие критериям (4), (5) и (6).

В рамках настоящего исследования не ставилась задача определить названые границы и величины шагов, для которых было бы доказано, что они обеспечивают оптимальное решение с заданной точностью. Эти характеристики были выбраны интуитивно на основе уравнения регрессии, полученного с использованием метода наименьших квадратов с учетом обнаруженной высокой корреляции между рассматриваемыми переменными. Расчеты проводились для коэффициента а, меняющего значения от 0,325 до 0,335 с шагом 0,005 и для параметра b – от 61,85 до 62,10 с шагом 0,05.

Ход проведенных расчетов можно проследить по представленным в табл. 2–4 фрагментам матриц, в которые заносились полученные при каждом сочетании а и b величины max и max .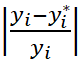

Таблица 2

Значения суммы модулей отклонений

(фрагмент матрицы)

Таблица 3

Максимальные значения модуля отклонений max

(фрагмент матрицы)

Таблица 4

Максимальные значения

модуля относительных отклонений max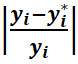

(фрагмент матрицы)

В таблице 5 представлены уравнения регрессии, параметры которых соответствуют критериям (3), (4), (5) и (6). Здесь же приведены соответствующие каждому из этих уравнений индексы отклонений, а также величины максимума абсолютных и относительных отклонений теоретических значений уровня экономической активности населения от наблюдаемых.

Таблица 5

Итоги расчетов

Приведенные в таблице 5 уравнения регрессии – это четыре варианта модифицированных функций предложения труда в России. Как видно из таблицы, различия между этими функциями невелики, но тем не менее они дают пищу для размышлений. Например, можно заметить, что выбирая функцию, основанную на критерии (4), мы в наибольшей степени поступаемся величиной максимального относительного отклонения, а ориентируясь на критерий (5), довольно существенно ухудшаем значение индекса отклонений.

Незначительно отличаются функции, базирующиеся на критериях (4), (5) и (6), и от регрессионного уравнения, параметры которого рассчитаны методом наименьших квадратов. Основываясь на том, что это уравнение характеризуется высоким значением коэффициента детерминации, можно утверждать, что и функции, построенные на основе предлагаемого в настоящей работе подхода, также достаточно адекватно отражают действительность.

Поскольку совокупность критериев, определяющих три варианта основанных на модулях отклонений функций предложения труда, представляет собой, по существу, многокритериальную задачу оптимизации, можно поставить вопрос о построении некоторого компромиссного варианта уравнения регрессии, учитывающего все три критерия оптимальности. Можно предложить несколько путей построения такого уравнения. Для примера мы выписали линейное уравнение, где коэффициент при W является средней арифметической из трех рассчитанных значений а, а свободный член – средней арифметической из трех величин b. Полученная таким образом функция имеет вид:

y=0,340W+62,07. (8)

Функция (8) характеризуется индексом отклонений, равным 0,41%, максимальным отклонением, равным 0,71 п.п., и максимальным относительным отклонением, равным 1,03%.

Как легко догадаться, сравнив темпы роста y и W, предложение труда на макроуровне характеризуется весьма низкой эластичностью. Расчеты показывают, что точечная эластичность всех построенных нами функций в 2016 г. составляла около 0,10. Понятную экономическую трактовку имеет коэффициент а в формуле (7). Рассчитанные нами его значения в различных вариантах уравнений регрессии, лежащие в интервале 0325–0,350, говорят о том, что повышение реальной заработной платы на 1 тыс. руб. приводит к увеличению уровня участия в рабочей силе чуть больше, чем на 0,3 п.п. Приведенные данные говорят о том, что добиться сколько-либо существенного роста экономической активности населения можно только при условии очень значительного увеличения средней заработной платы.

Завершая настоящий раздел статьи, заметим, что величина предложения труда S, основанная на модифицированных функциях предложения, определяется по простой формуле:

S=0,01y×N, (9)

где N– численность населения в возрасте от 15 до 72 лет, выраженная в тех же единицах измерения, что S.

Выражение (9) представляет собой двухфакторную функцию предложения труда на макроуровне.

Заключение

Подводя итоги проделанной работы, можно констатировать, что построенные и традиционным, и описанным в статье альтернативным способом модифицированные функции предложения труда в России определяют целесообразность существенного повышения заработной платы, если ставить задачу заметного повышения экономической активности населения. Увеличение заработной платы, как было показано в публикации Винокурова Е.Ф. [2] (Vinokurov, 2021), должно привести к росту численности занятых, а тем самым и ВВП, т.е. обеспечить выход российской экономики из состояния рецессии, причем инфляционное давление оказывается приемлемым.

Что касается рассмотренного в настоящей статье нестандартного подхода к определению параметров уравнений регрессии, то представляется, что дальнейшая работа в этой области должна быть направлена на строгую формулировку методов определения границ рассматриваемых в ходе расчетов значений этих параметров. Решение этой задачи позволило бы в некоторых случаях существенно сократить объем этих расчетов. Далее желательно накопление опыта построения уравнений регрессии на основе альтернативного подхода. Такой опыт позволил бы определить уровень значений предложенного для оценки адекватности моделей показателя, позволяющий признать модель адекватной действительности. И наконец, если исследователь примет решение использовать предложенный подход к проблеме, нужно будет разработать соответствующее программное обеспечение.