Моделирование деятельности высокотехнологичного инновационного предприятия при помощи производственной функции типа Кобба – Дугласа

Зависимость величины выпуска какой-либо продукции от факторов производства описывается производственной функцией. Наиболее универсальной функцией является функция типа Кобба – Дугласа, с помощью которой можно моделировать системы различных уровней от небольших предприятий до национальных экономик. Впервые она была применена в 1928 году американскими экономистами Ч. Коббом и П. Дугласом при анализе влияния затрачиваемого капитала и труда на объем выпускаемой продукции в обрабатывающей промышленности США. Функция Кобба – Дугласа выглядит следующим образом:

K – затраты капитала (или основные фонды), выраженные в денежных единицах;

L – затраты на труд (характеризует количество работников);

A – производственный коэффициент, показывающей пропорциональность факторов производства и объема выпускаемой продукции;

α, β – коэффициенты эластичности производства по капиталу и труду соответственно.

Как отмечалось выше, производственная функция типа Кобба – Дугласа является достаточно универсальной и применимой к экономическим системам разных масштабов. Однако большая часть работ российских специалистов по данной теме применяет производственную функцию для моделирования экономик субъектов Российской Федерации или страны в целом [1–7] (Kirilyuk, 2013; Pshenichnikova, Romanyuk, 2017; Gafarova, 2013; Kleshcheva, 2020; Beilin, 2019; Zvereva, Lukashenok, 2019; Sirotkin, Zhelenkova, Kozhevnikova, Chikurova, 2019). В работе [8] (Vinogradov, Pyhteeva, Petrov, Abdurakhmanova, Trofimov, 2019) авторы доказывают применимость классической производственной функции типа Кобба – Дугласа (т.е. параметрами которой являются величина основных фондов и затраты на труд) для моделирования деятельности 6 российских предприятий различных отраслей экономики (промышленность, сельское хозяйство, лесное хозяйство, грузовой транспорт, торговля, общественное питание).

В настоящей работе авторами была поставлена цель – создание модели высокотехнологичного инновационного предприятия аэрокосмической отрасли с помощью расширенной производственной функции типа Кобба – Дугласа и выдвинута гипотеза об увеличении достоверности данной модели по сравнению с моделью на основе классической производственной функции типа Кобба – Дугласа.

Высокотехнологичные предприятия (т.е. предприятия, выпускающие не менее 50% высокотехнологичной продукции) имеют ряд отличительных особенностей [9] (Goraeva, Shamina, 2014), а именно:

1. Необходимость проведения НИОКР на протяжении всего жизненного цикла предприятия, а также на всех стадиях жизненного цикла продукта.

2. Значительная доля высококвалифицированного промышленно-производственного персонала и инженерно-технических работников в общей численности занятых.

3. Высокий удельный вес интеллектуальной собственности в составе активов предприятия в виде патентов, лицензий, авторских прав на изобретения, промышленных образцов и т.д.

4. Повышенное качество технологического процесса, наличие прецизионных технологий и технологических инноваций.

5. Наличие инновационной продукции.

6. Повышенный риск проектов, связанных с разработкой и внедрением новой высокотехнологичной продукции.

7. Значительная роль неценовых конкурентных факторов в развитии предприятий.

Согласно [10] (Gavrilova, 2014), компании, считающиеся высокотехнологичными, образуют высокотехнологичные отрасли, перечень которых представлен в таблице 1.

Таблица 1

Классификация высокотехнологичных отраслей

Можно заметить, что ни одна из отраслей в работе [8] (Vinogradov, Pyhteeva, Petrov, Abdurakhmanova, Trofimov, 2019) не относится к высокотехнологичной, а значит, нельзя распространить ее результаты на высокотехнологичные компании. Помимо этого авторы считают, что для моделирования деятельности наукоемких предприятий необходимо инсталлировать в производственную функцию типа Кобба – Дугласа ряд показателей, связанных с признаками, перечисленными выше.

В условиях импортозамещения в российской экономике резко выросла потребность в ускоренной разработке и выпуске инновационной и конкурентоспособной продукции для внутреннего рынка. Согласно [11] (Vostrikov, 2015), инновации являются важнейшим внутренним резервом экономического роста страны, а высокотехнологичные компании должны стать локомотивами, способными вывести экономику на траекторию технологического прорыва. Также большим опытом исследований роли высокотехнологичных предприятий в российской экономике обладают авторы [12, 13] (Andrusenko, Yamchenko, Karpenko, Sokolyanskiy, 2016; Sokolyanskiy, Pashkov, 2015). Для стабильного роста и устойчивой работы таких предприятий в условиях различных экономических и политических турбулентностей необходимо иметь в арсенале действенные методы прогнозирования, оптимизации затрат и оценки влияния различных факторов производства на объемы выпускаемой продукции. Поэтому моделирование деятельности высокотехнологичных предприятий является актуальной темой в условиях сложившейся экономической ситуации.

Объектом настоящего исследования являются два высокотехнологичных инновационных предприятия аэрокосмической отрасли, а именно: The Boeing Company и АО «НПО Энергомаш» им. академика В.П. Глушко (далее – НПО «Энергомаш»).

Американская компания The Boeing Company основана в 1916 году и специализируется на производстве широкого спектра гражданской и военной авиационной техники, являясь наряду с Airbus крупнейшим производителем самолетов в мире. Кроме того, компания выпускает широкий спектр авиационно-космической техники военного назначения (в том числе вертолеты), ведет широкомасштабные космические программы. Основными клиентами американской корпорации являются крупные авиакомпании (Luftwaffe, Britannia Airways, S7 Airlines, «Аэрофлот» и др.), министерство обороны США, NASA.

НПО «Энергомаш» была основана в 1929 году и является организацией в составе Газодинамической лаборатории (ГДЛ) в Ленинграде по разработке ракет, а также электрических и жидкостных ракетных двигателей под руководством В.П. Глушко. Основной продукцией предприятия являются жидкостные ракетные двигатели для тяжелых, средних и малых ракетоносителей. Главным заказчиком является Роскосмос, но компания также сотрудничает с NASA, KARI и др.

В ходе выполнения работы использовались данные из открытых источников, в том числе официальных сайтов компаний и корпоративных журналов. Показатели, необходимые для создания классической производственной функции, представлены в таблицах 2 и 3.

Таблица 2

Параметры для создания классической производственной функции для предприятия The Boeing Company

Таблица 3

Параметры для создания классической производственной функции для предприятия НПО «Энергомаш»

Достаточно распространенным способом нахождения неизвестных коэффициентов в функции Кобба – Дугласа является метод наименьших квадратов (МНК). Сущность МНК заключается в минимизации суммы квадратов отклонений реально наблюдаемых значений выпуска продукции от их оценок, полученных с помощью линии регрессии. Метод наименьших квадратов применяется к уравнению линейной регрессии, связывающему логарифмы исходных данных.

Показатели в производственной функции были найдены с помощью функции «ЛИНЕЙН» в программе MS Excel. Для компании The Boeing Company производственная функция имеет вид (2), для НПО «Энергомаш» (3).

Сопоставление фактического объема продаж компаний с рассчитанным при помощи производственной функции представлено на рисунках 1, 2. Из них видно, что классическая производственная функция достоверно описывает деятельность высокотехнологичного предприятия.

Авторы заменили показатель «среднесписочная численность персонала» на «среднесписочную численность высококвалифицированного персонала» и ввели в рассмотрение такой показатель, как НИР-мультипликатор (отношение затрат на разработку нового продукта к капитальным вложениям в производство и реализацию этого продукта).

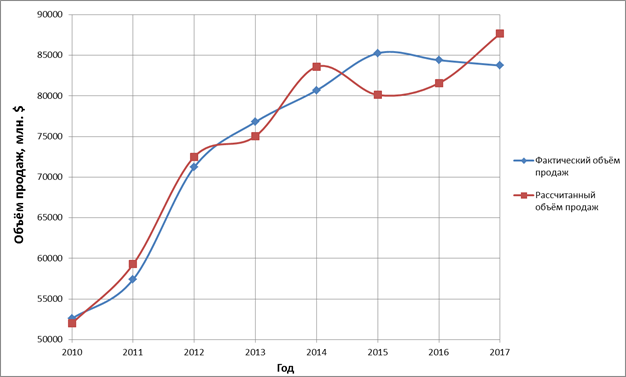
Рисунок 1. Объемы продаж компании The Boeing Company по годам

Источник: составлено авторами.

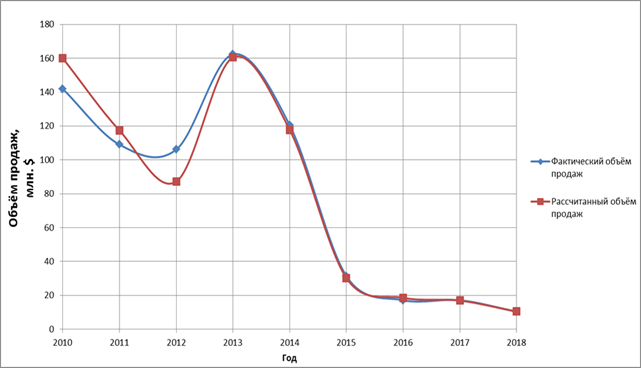
Рисунок 2. Объемы продаж компании НПО «Энергомаш» по годам

Источник: составлено авторами.

Помимо вышесказанного в ряде источников [16, 17] (Kazakova, Sinelnikov-Murylev, 2009; Podkorytova, Alekseev, Chigvintseva, 2011) отмечается большое влияние рынка нефти на деятельность российских предприятий, поэтому авторами введен еще один множитель, отражающий цену на нефть марки Urals для НПО «Энергомаш» и цену на нефть марки Brent для The Boeing Company.

Показатели, необходимые для создания модифицированной производственной функции, представлены в таблицах 4, 5.

Авторами была предложена модифицированная производственная функция, имеющая следующий вид:

величина основных фондов;

численность высококвалифицированного персонала;

НИР-мультипликатор;

цена барреля нефти марки Brent для американской компании и марки Urals – для российской;

рассчитываемые коэффициенты.

Таблица 4

Параметры для создания модифицированной производственной функции для предприятия The Boeing Company

Таблица 5

Параметры для создания модифицированной производственной функции для предприятия НПО «Энергомаш»

Производственная функция без учета цены на нефть имеет вид (4) и (5) для The Boeing Company и НПО «Энергомаш» соответственно, а с учетом цены на нефть – вид (6) и (7).

Достоверность полученных моделей высокотехнологичных предприятий определяется с помощью методов математической статистики. Для оценки созданных моделей, полученных на основе МНК, используются показатели: коэффициент детерминации (R²), скорректированный коэффициент детерминации и критерий Фишера (F_расч.), которые представлены в таблице 6. Данные показатели рассчитываются программой MS Excel при вычислении коэффициентов линейной регрессии.

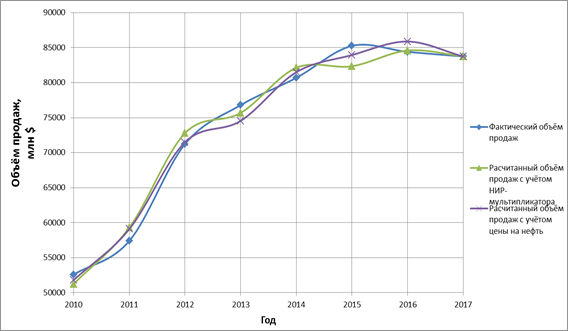
Рисунок 3. Объемы продаж компании The Boeing Company по годам

Источник: составлено авторами.

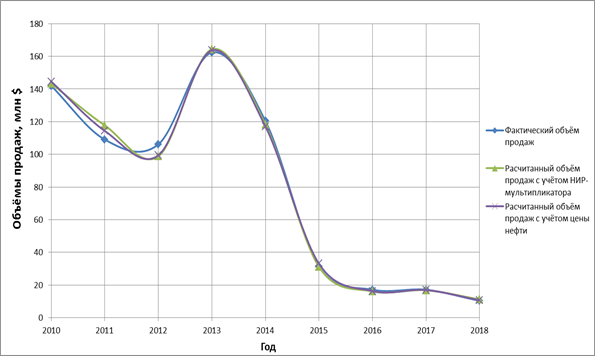
Рисунок 4. Объемы продаж компании НПО «Энергомаш» по годам

Источник: составлено авторами.

Считается, что регрессионная модель должна объяснять не менее 80% вариации зависимой переменной, то есть модель успешна, если R² ≥ 0,8 [1] (Kirilyuk, 2013). Скорректированный R² необходим для сравнения моделей с различным числом параметров, так как при увеличении их количества R² увеличивается, даже если эти переменные не имеют отношения к рассчитываемой величине.

Таблица 6

Точность аппроксимации данных производственной функции

На основе проведенного исследования можно сделать ряд выводов: классическая производственная функция типа Кобба – Дугласа применима для моделирования деятельности ВТК, предложенная авторами модифицированная производственная функция точнее описывает экономику инновационных высокотехнологичных предприятий аэрокосмической отрасли, так как она включает в себя показатели, имеющие высокое значение для наукоемких предприятий (численность высококвалифицированного персонала, НИР-мультипликатор).

Полученные производственные функции могут быть применены для анализа влияния различных факторов на объемы выпускаемой продукции высокотехнологичных предприятий различных отраслей, прогнозирования соотношения объемов выпуска и объемов факторов производства, оптимизации затрат предприятия и оценки зависимости деятельности компании от цены на энергоносители.