Нечетко-множественная модель IT-кластера (на примере Ростовской области) на основе модифицированной модели Леонтьева

Введение

Кластер информационно-коммуникационных технологий (ИКТ-кластер) Ростовской области был создан в 2015 году. В настоящее время он включает в себя 25 участников, среди которых: 1) средние производственные предприятия, от 101 до 150 работников, такие как ГК «Гендальф», ЗАО «Медиапарк Южный регион», ООО Научно-производственное предприятие «ВНИКО»; 2) малые производственные предприятия, до 100 работников, такие как ООО «АйТи Сервис», ООО «БНВ Инжениринг», ООО «Интернет-Фрегат», ООО «Проф ИТ», ООО «РНД Софт», ООО «Риттал» (Ростовское отделение), ООО «Фаст Репортс», ЗАО «ЮБиТек», ООО Научно-производственное предприятие «Интор», ООО Научно-производственный центр «Космос 2», ООО Специальное конструкторское бюро «Граф»; 3) крупное производственное предприятие (более 250 работников) ПАО Ростовское отделение Кавказского филиала ПАО «МегаФон»; 4) вузы ФГБОУ ВО «Ростовский государственный экономический университет (РИНХ)» и ФГБОУ ВО «ЮРГПУ (НПИ) им. М.И. Платова»; 5) другие учебные заведения, НОУ ДПО «Ростовский центр повышения квалификации в области информационных технологий и связи» и ГБПОУ РО «Ростовский-на-Дону колледж связи и информатики»; 6) корпорация развития, агентство, НП «Единый региональный центр инновационного развития Ростовской области», Инновационно-технологический центр «ИнТех-Дон», РОФССЭР «Танаис» (Региональный институт развития), Союз Торгово-промышленная палата Ростовской области (Региональный институт развития); 7) финансово-кредитная организация ОАО коммерческий банк «Центр-инвест».

Главной целью ИКТ-кластера является создание в Ростовской области полноценной экосистемы для развития и коммерциализации проектов своих резидентов в области ИКТ-технологий. Среди приоритетных целей создания ИКТ-кластера: повышение благосостояния и качества жизни населения области на основе развития современных информационно-коммуникационных технологий; повышение эффективности и конкурентоспособности различных сфер экономики региона в результате использования современных информационных технологий; увеличение вклада отрасли информационных технологий Ростовской области в валовой региональный продукт; рост эффективности государственного управления, повышение качества предоставления государственных и муниципальных услуг в Ростовской области.

К приоритетам развития кластера относят: 1) организационное развитие кластера и усиление кооперационных связей между участниками (потенциала взаимодействия); 2) развитие инновационного потенциала и сектора исследований и разработок; 3) развитие производственного потенциала и расширение рыночной доли продукции и услуг участников кластера; 4) развитие кадрового потенциала; 5) формирование общего бренда и повышение узнаваемости кластера (маркетинговый потенциал); 6) развитие связей с органами власти (управленческий потенциал) [1, 6, 8] (Andreeva, Astanina, 2019; Kosheleva, 2020; Mukhamadeev, 2020).

Важной задачей является математическая формализация внутрикластерных взаимодействий структурных единиц кластера, приводящих к изменению потенциалов как его в целом, так и отдельных предприятий, а также его внешних взаимодействий [4, 7, 11] (Kamyshnikova, 2019; Morkovkin, Nikogosyan, Dontsova, 2020; Ryabchikova, 2020). Для данной цели предполагается использовать модифицированную балансовую модель Леонтьева, входные параметры которой получены на основе открытых источников данных, а также агрегирования фаззификации на основе теории нечетких множеств. Под кластером в математическом моделировании может подразумеваться группа предприятий и организаций, действующих в определенном виде производства и на определенных нишах рынка, что при объединении их в кластер позволяет получить специфические конкурентные преимущества [2, 3, 9, 10] (Groshev, Pelikhov, 2019; Naydenov, Spiryagin, Novokshonova, 2015; Nedosekin, 2003).

1. Модифицированная модель Леонтьева для кластера

Рассмотрим более подробно предлагаемую нами модель [5] (Kramarov, Pelikhov, Sakharova, Khramov, 2019). Пусть кластер состоит из n предприятий, каждое из которых имеет пять потенциалов: производства , взаимодействия , инновационный , кадровый , маркетинговый , управления: , . Будем считать, что часть каждого из пяти потенциалов каждого из участников кластера расходуется либо на взаимодействие в процессе производства с каждым из других объектов кластера, либо остается в резерве, а другая часть направлена на сторонние взаимодействия. Для этой цели введем в рассмотрение сторонний потенциалы , .

Сторонний потенциал может быть результатом как внутреннего, так и внешнего взаимодействия. Внутренняя составляющая является результатом взаимодействия с остальными участниками кластера: обмена технологиями и информацией, наращивания либо уменьшения продаж за счет консолидации либо конкуренции с предприятиями (конкурентных потенциалов), привлечения инноваций за счет научных центров кластеров (инновационного и технологического потенциала кластерных центров), а также высококвалифицированных кадров (кадровый потенциал). Он может быть также увеличен за счет маркетингового потенциала сервисных компаний и ресурсного потенциала вспомогательных компаний.

Внешняя составляющая стороннего потенциала будет состоять из по меньшей мере трех частей (региональной, межрегиональной и международной). Соответствующие потенциалы взаимодействий, очевидно, будут задаваться извне (потенциалы организационной, инвестиционной и политической поддержки на региональном уровне; конкурентные, маркетинговые и производственные потенциалы аналогичных кластеров на межрегиональном уровне; конкурентные, информационные и маркетинговые потенциалы, а также потенциалы политического влияния на международном уровне). Изменение внешнего конкурентного потенциала как на межрегиональном, так и на международном уровне в процессе кластеризации вызывает наращивание внутрикластерных потенциалов: интеллектуального, инновационного, маркетингового, управленческого и др.

Введем обозначения: например, – часть совокупного производственного потенциала управления -го предприятия, направленного на взаимодействие с -м предприятием кластера ( ; ).

Предположим, что совокупный производственный потенциал объекта равен сумме всех его потенциалов, направленных на производственные взаимодействия внутри кластера и стороннего потенциала. Тогда получим систему уравнений вида:

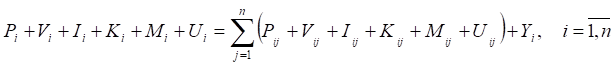. (1)

Уравнение (1) назовем соотношениями баланса потенциалов внутри кластера.

Ведем коэффициенты собственных потенциалов, например:

. (2)

Тогда, после преобразований соответствующую систему уравнений можно записать в матричном виде, аналогичном тому, что известен для балансовой модели Леонтьева:

. (3)

Уравнение (3) назовем уравнением линейного баланса потенциалов внутри кластера. Как и балансовая модель Леонтьева, оно позволяет решать две основные задачи:

1) расчет сторонних потенциалов в случае, когда известны коэффициенты собственных потенциалов;

2) расчет каждого из шести потенциалов отдельных предприятий (или их групп), когда известны сторонние потенциалы.

Математический аппарат для решения классической модели Леонтьева широко известен. В то же время в рассматриваемой интерпретации достаточно сложно определить точные значения входных величин с учетом экспертных оценок. Существенно, что экспертные оценки позволяют определить потенциалы в виде нечетких треугольных чисел, то есть вариантов пессимистического, среднего ожидаемого и оптимистического значений.

2. Нечетко-множественная интерпретация модели

Рассмотрим систему линейных уравнений с интервальными коэффициентами:

Для решения данной системы уравнений можно использовать, например, следующий итерационный алгоритм:

1. Выбирается расширенный вектор решения , который можно представить в виде:

.

2. Вычисляется расширенный вектор свободных членов:

. (4)

3. Исключая из (4), получаем систему обыкновенных линейных уравнений относительно приращений , которая решается одним из известных способов (например, методом исключения).

4. Определяется уточненный вектор :

.

5. Снова вычисляется расширенный вектор свободных членов:

.

6. Проверяется критерий окончания счета

,

где x – заданная точность.

7. Если условие 6 выполняется, то расчет заканчивается, иначе переходят к этапу 3.

Для решения системы нелинейных уравнений может использоваться также итерационный метод с линеаризацией уравнений на каждом шаге итерации по одному из известных способов (например, методом Ньютона).

Заключение

Чтобы свести воедино в модели разнородные потенциалы, их необходимо унифицировать. Поэтому для моделирования предлагается использовать мягкие модели. Предлагается оценивать потенциал в виде лингвистической переменной, имеющей пять термов [10] (Nedosekin, 2003), которым присваивается нумерация. Соответственно, решение осуществляется не для самих потенциалов, а для их нечетко-множественных оценок, производимых с помощью функций принадлежности. Кроме того, вместо обычного перемножения матриц можно использовать максиминную (минимаксную) свертки, а исходные данные представлять в виде нечетких множеств.