Модель Wonderland как вспомогательный инструмент регулирования экономико-экологического развития

Введение

В результате бурного развития промышленности и стремительного роста населения все чаще некоторые города-мегаполисы и даже целые страны оказываются на грани экологической катастрофы. Пагубное воздействие на окружающую среду оказывают многие виды деятельности человека, включая добычу ископаемых, сжигание источников энергии, вырубку лесов, использование автотранспорта и т.д. Особо негативные последствия несут выбросы промышленных отходов и вредных токсичных веществ в атмосферу. В результате слива грязных и токсичных вод в реки, озера и моря происходит загрязнение гидросферы. Все сильнее обостряется проблема утилизации твердых бытовых отходов, что влечет увеличение числа мусорных свалок.

Необходимость решения возникающих экологических проблем обуславливает актуальность разработок экономико-математических моделей, которые позволяют имитировать и анализировать возможные сценарии экономического развития человечества с учетом изменения окружающей среды. Одной из наиболее известных таких разработок является модель Wonderland («Чудесная страна»), предложенная в 1994 году В. Сандерсоном [9, 10] (Sanderson, 1994). Эта модель способна имитировать различные взаимосвязанные экономические, демографические и экологические процессы. Впоследствии для модели Wonderland были предложены разнообразные модификации [3] (Groller, Wegenkittl, Milik, Prskawetz, Feichtinger, Sanderson, 1996), [4, 6] (Herbert, Leeves, 1998, 2002), [7] (Lempert, Popper, Bankes, 2003), [5] (Kohring, 2006), [1] (Zvyagintsev, 2020).

В этой статье будет получена еще одна модификация модели Wonderland, основанная на современных методах теории управления хаосом. Эти методы позволяют преодолевать катастрофическую динамику и формируют устойчивую периодическую траекторию экономико-экологического развития.

Для практического применения модифицированной модели Wonderland будет использоваться экономическая статистика США. Выбор этой страны в качестве наглядного примера обусловлен следующими противоречивыми факторами. Экономика США является ведущей на мировой арене, американский ВВП составляет пятую часть мирового ВВП. США находятся в авангарде технологической революции. Понятие экологии как науки зародилось именно в США. Все американские президенты позиционируют свою страну как эталонный образец развития для всего человечества. Но при этом экологическая обстановка в США далека от идеала. Американские мегаполисы Нью-Йорк, Чикаго и Лос-Анджелес входят в число самых экологически опасных городов мира. США опережают многие страны, включая Россию, по уровню выброса СО₂. Интенсивная добыча сланцевой нефти наносит серьезный вред экологии Соединенных Штатов. Более того, на протяжении многих лет США отказываются ратифицировать Киотский протокол о сокращении выбросов парниковых газов в атмосферу Земли, а в 2019 году Соединенные Штаты объявили о выходе из Парижского соглашения по климату.

В данной работе будет предложен новый научный метод, способный дополнить комплекс мероприятий по борьбе с возможными экономико-экологическими кризисами. На базе модели Wonderland будет сконструирована оригинальная экономико-математическая модель, позволяющая генерировать математически формализованные рекомендации по преодолению кризисных ситуаций. Научная и практическая ценность этой модели заключается в том, что она дает возможность определять точные сроки и затраты антикризисных мероприятий.

Отметим, что данная статья является дополнением к циклу работ [4, 6] (Herbert, Leeves, 1998, 2002), [7] (Lempert, Popper, Bankes, 2003), [5] (Kohring, 2006), [1] (Zvyagintsev, 2020), посвященных поиску возможностей по преодолению экономико-экологических катастроф.

Одним из основных индикаторов уровня развития страны считается величина ВВП на душу населения. На основании находящихся в открытом доступе официальных статистических данных по США [13] построим график для темпов прироста ВВП на душу населения этой страны.

Темпы прироста ВВП на душу населения США будем обозначать , где – номинальный ВВП на душу населения в j-й год. Из рисунка 1 видно, что в период с 1994 по 2003 год наблюдаются 3 трехлетние волны однообразной формы, но различной амплитуды. В последующий период времени цикличность нарушается и доминирует хаотичная динамика.

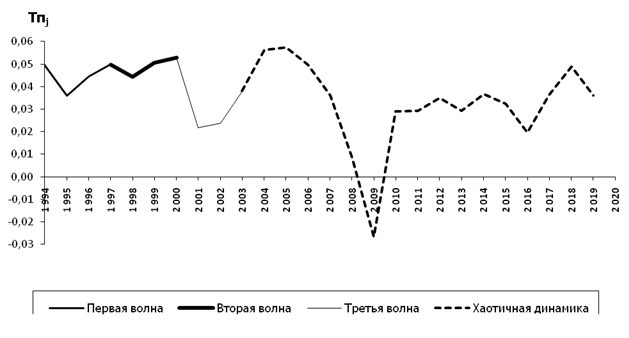
Рисунок 1. Темпы прироста ВВП на душу населения США

Источник: U.S. Real GDP Statistics [13].

Для моделирования экономико-экологических процессов в качестве базовой воспользуемся моделью Wonderland [9, 10] (Sanderson, 1994), математическая запись которой имеет следующий вид:

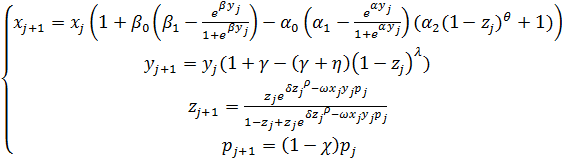(1)

Здесь коэффициенты являются положительными константами; j = 0, 1, 2, …; – темпы прироста населения; – темпы прироста ВВП на душу населения; – природный капитал; – загрязнение на единицу продукции.

В модели Wonderland первое уравнение описывает динамику численности населения с использованием коэффициентов рождаемости и смертности. Второе уравнение отражает динамику уровня производства с учетом запаса природного капитала. Третье уравнение характеризует качество окружающей среды и задает рост природного капитала по логистическому закону. Условный показатель экологического состояния изменяется в пределах от нуля до единицы. В случае считается, что экология находится в идеальном состоянии и полностью отсутствует загрязнение окружающей среды. Значение выражает противоположный предельный случай, когда загрязнение окружающей среды настолько велико, что возникает максимальная угроза для человеческого здоровья и экономики. Четвертое уравнение указывает на уровень технологичности производства и выполняет функцию управления интенсивностью загрязнения окружающей среды. Гипотетический показатель загрязнения на единицу продукции изменяется в пределах от нуля до единицы. Значение соответствует наивысшей степени загрязнения на единицу продукции. Если же , то загрязнение на единицу продукции отсутствует, что указывает на очень высокий уровень технологичности производства.

Четвертое уравнение системы (1) представляет собой формулу геометрической прогрессии. Поскольку положительный коэффициент χ выбирается меньше единицы, то со скоростью убывающей прогрессии быстро стремится к нулю. Такой сценарий для процессов загрязнения является идеальным, но вряд ли соответствует современным реалиям. Трудно ожидать, что в ближайшие два-три десятилетия произойдет такая технологическая революция, что уровень загрязнения упадет почти до нуля. Более реалистично предполагать, что загрязнение сократится в разы и уменьшится до приемлемо низкого уровня. В этой связи произведем замену четвертого уравнения системы (1) на уравнение следующего вида:

. (2)

На рисунке 2 графически изображены решения уравнения (2) и четвертого уравнения системы (1) для значений χ = 0,05 и ε = 0,01.

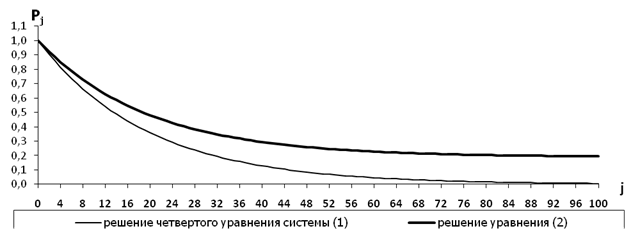
Рисунок 2. Графики решений уравнения (2) и четвертого уравнения системы (1)

Источник: составлено автором.

Модель (1) после замены четвертого уравнения принимает следующий вид:

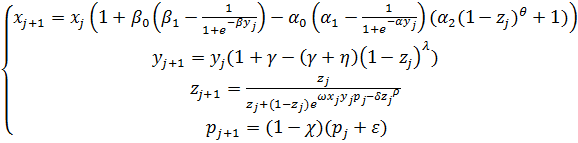(3)

Для рассматриваемой системы (3) в результате компьютерного эксперимента были подобраны численные значения параметров:

.

С помощью приближенных методов для нелинейной дискретной системы (3) была найдена периодическая орбита с периодом 3, имеющая следующие координаты:

.

Необходимо отметить, что для нахождения этого 3-цикла потребовалось вычислить все его координаты с точностью до 15-го знака после запятой.

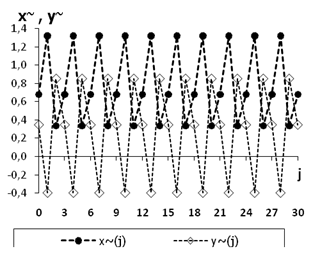
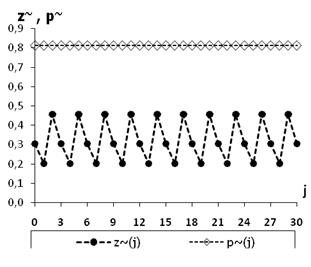Рисунок 3. Периодическое решение дискретной системы (3)

Источник: составлено автором.

Нелинейная система (3) отличается очень высокой чувствительностью к изменениям начальных условий. Даже незначительные изменения начальных данных влекут существенные перемены в поведении решений. Так, совершив для корректировку в третьем знаке после запятой, получили следующий график для темпов прироста ВВП на душу населения :

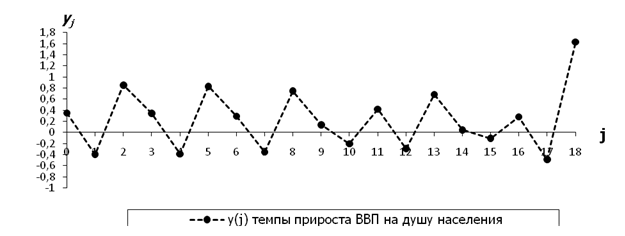
Рисунок 4. Смоделированные темпы прироста ВВП на душу населения

Источник: составлено автором.

Из этого графика видно, что вначале существуют три волны с периодом 3, а затем цикличность нарушается и наступает хаотичное движение. Сравнение рисунков 1 и 4 демонстрирует схожесть поведения реальных и смоделированных темпов прироста ВВП на душу населения. Таким образом, за счет варьирования начальных условий дискретная система (3) способна имитировать сценарии, которые вполне соответствуют реальным экономическим процессам.

В результате верификации были подобраны нормировочные коэффициенты и для и соответственно. По формуле

(4)

был смоделирован периодический тренд для номинального ВВП на душу населения США, где – величина американского ВВП на душу населения по итогам 1993 года. Коэффициент корреляции между смоделированным периодическим трендом и реальным ВВП на душу населения США составляет 0,978 и является статистически значимым, поскольку по критерию Стьюдента t_набл = 23,441 больше t_крит = 2,787 при уровне значимости α = 0,005.

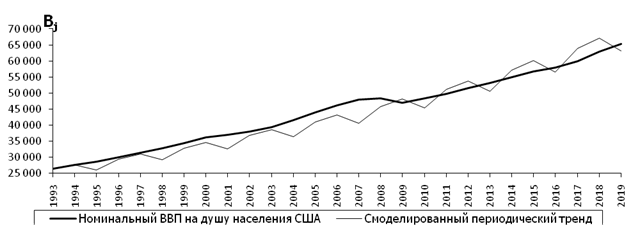
Рисунок 5. Фактический американский ВВП на душу населения и смоделированный периодический тренд

Источник: составлено автором.

По формуле

(5)

был смоделирован периодический тренд для численности населения США, где – номинальная численность американского населения на конец 1993 года. Коэффициент корреляции между смоделированным периодическим трендом и фактической численностью населения США составляет 0,994 и является статистически значимым, поскольку по критерию Стьюдента t_набл = 45,438 превышает t_крит = 2,787 при уровне значимости α = 0,005.

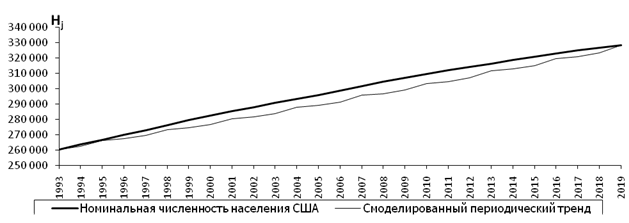
Рисунок 6. Фактическая численность населения США и смоделированный периодический тренд

Источник: составлено автором.

Для смоделированных системой (3) экологических характеристик получилось, что природный капитал колеблется в диапазоне от 0,20241 до 0,45642, а загрязнение на единицу продукции удерживается на уровне 0,8127. Поскольку существенно меньше единицы, а заметно превосходит ноль, то можно заключить, что экологическая обстановка в США еще далека от идеального состояния. Это вполне соответствует современным реалиям. Таким образом, полученные результаты показывают, что сконструированная модель (3) – (5) является вполне адекватной и хорошо адаптированной к реальным процессам, наблюдаемым в США. Эта модель способна с высокой точностью имитировать американскую экономико-экологическую динамику.

Воспользуемся полученной моделью (3) – (5) в целях построения долгосрочного прогноза для США. По оценкам Международного агентства S&P Global (S&P) по итогам 2020 года, ожидается снижение ВВП США на 5% [12]. Это обусловлено падением производства, ростом банкротств, скачком безработицы в результате пандемии COVID-19, а также ростом социальной напряженности на фоне расовых проблем. Высокая смертность от коронавируса и миграционный отток в результате экономического кризиса, рекордной безработицы и социальных волнений в американских городах приведут к снижению населения. Это снижение может составить порядка одного процента. Сокращение производства, банкротства компаний по добыче сланцевой нефти, отток мигрантов должны улучшить экологическую обстановку. На основании вышеперечисленных предположений по итогам 2020 года можно для системы (3) задать следующие начальные данные:

= – 0,01; = – 0,045; = 0,5; = 0,75. (6)

Осуществим для США прогнозирование на долгосрочную перспективу до конца текущего столетия. Для этого решим систему (3) с начальными условиями (6) и по аналогии (4) – (5) применим формулы:

, (7)

В результате получаются следующие прогнозные графики.

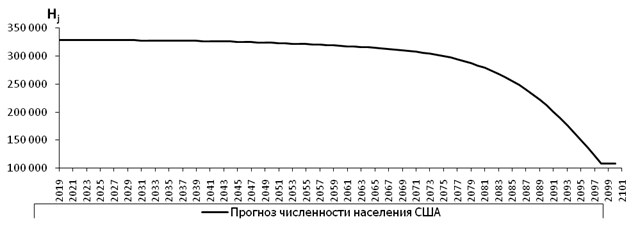
Рисунок 7. Долгосрочный прогноз численности населения США

Источник: составлено автором.

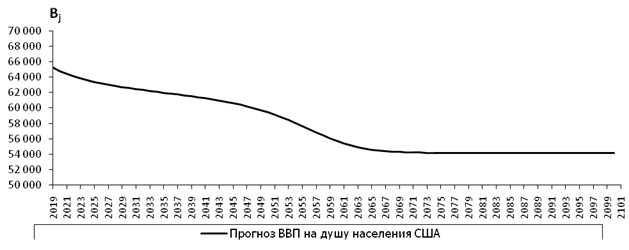
Рисунок 8. Долгосрочный прогноз ВВП на душу населения США

Источник: составлено автором.

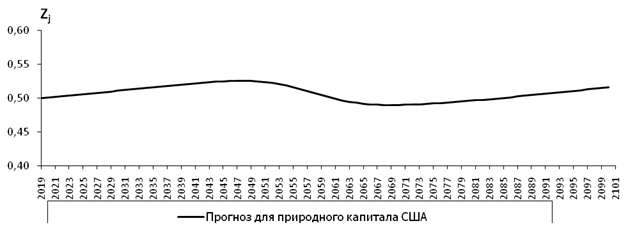
Рисунок 9. Долгосрочный прогноз для природного капитала США

Источник: составлено автором.

Построенный для США долгосрочный прогноз имеет катастрофический характер. Рисунок 7 демонстрирует стремительное сокращение численности населения США в три раза с 328,5 до 107,6 миллионов человек к 2100 году. Из рисунка 8 следует устойчивое снижение ВВП на душу населения с 65,2 до 54,1 тысяч долларов, то есть на протяжении 80 лет будет происходить стабильное обеднение американцев. При этом, как показывает рисунок 9, экология страны в течение 80 лет практически не изменится в лучшую сторону и будет колебаться около среднего уровня. Очевидно, что для США результатом такого сценария станет утрата статуса ведущей и высокоразвитой державы.

В условиях глубокого и затяжного кризиса не имеет смысла надеяться на рыночное саморегулирование, при котором «невидимая рука рынка» все чудесным образом восстановит и стабилизирует. В случае возникновения угрозы катастрофического сценария актуальной становится проблема поиска возможностей для преодоления кризисных явлений. В целях моделирования таких возможностей осуществим модификацию системы (3) с помощью современных методов теории управления хаосом.

Введем обозначения:

и представим систему (3) в векторной форме:

, (8)

где

; .

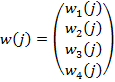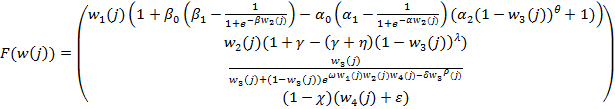Покажем, что подавления возможных кризисных сценариев можно добиться за счет применения функции управления U(j) и использования модифицированной системы:

. (9)

С помощью математических методов современной теории управления хаосом сконструируем функцию управления U(j), которая способствует преодолению кризисной тенденции, а затем обеспечивает восстановление и стабилизацию положительной динамики экономико-экологического развития.

Если совершить линеаризацию системы (8) в окрестности найденного 3-цикла с координатами , а затем применить метод Пирагаса [11] (Pyragas, 1992), то получим модифицированную систему (9), где U(j) является функцией управления, предназначенной для стабилизации поведения решений системы. На основании результатов работ [2] (Leonov, Zvyagintseva, 2015) и [8] (Leonov, Zvyagintseva, Kuznetsova, 2016) по стабилизации дискретных систем получим функцию управления следующего вида:

. (10)

Здесь P(j) – периодичная матрица следующего вида:

,

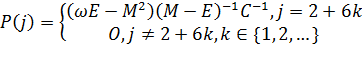где , E – единичная матрица, О – нулевая матрица, – матрица монодромии, , – матрица Якоби.

Для рассматриваемой вектор-функции F(w) матрица Якоби имеет следующий вид:

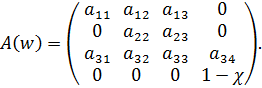
Здесь

,

,

,

, ,

, ,

, .

Покажем, что для полученного американского кризисного прогноза модифицированная система (9) дает возможность моделировать преодоление кризиса и последующий процесс стабилизации, в результате которой формируется устойчивый трехпериодичный режим. В целях нейтрализации кризиса первоочередной задачей является достижение годового прироста населения и ВВП на душу населения на уровнях, близких к значениям и для произвольного j из множества {0,1,2}. Предположим например, что по итогам 2021 года в результате использования государственных рычагов управления и реализации различных мер по мотивации экономико-демографического подъема удастся получить рост населения на 0,75% и рост ВВП на душу населения в размере 5,24%. Экстренное достижение таких показателей с большой вероятностью приведет к снижению качества окружающей среды и ухудшению экологических характеристик. Исходя из этих предпосылок и учитывая нормировочные коэффициенты, зададим следующие начальные условия:

. (11)

Решив модифицированную систему (9) с начальными условиями (11) и по аналогии (7) применив формулы:

, ,

получим представленные на рисунках 10–12 графики.

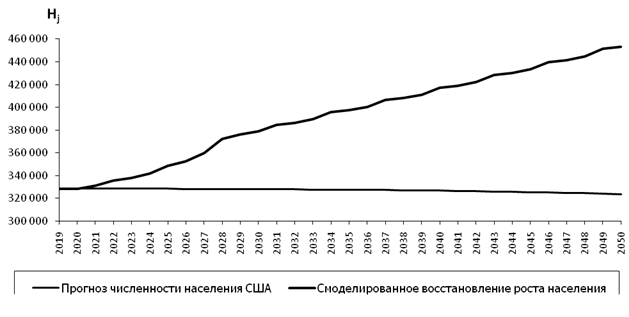
Рисунок 10. Смоделированное восстановление роста численности населения США

Источник: составлено автором.

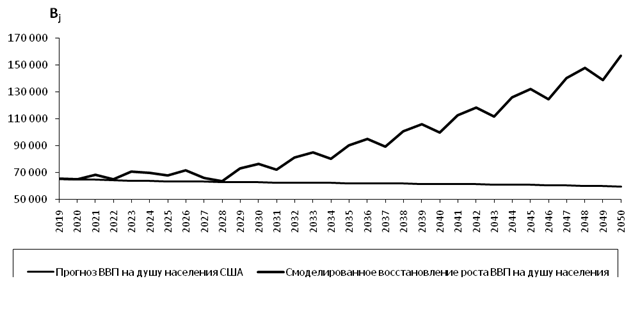
Рисунок 11. Смоделированное восстановление роста ВВП на душу населения США

Источник: составлено автором.

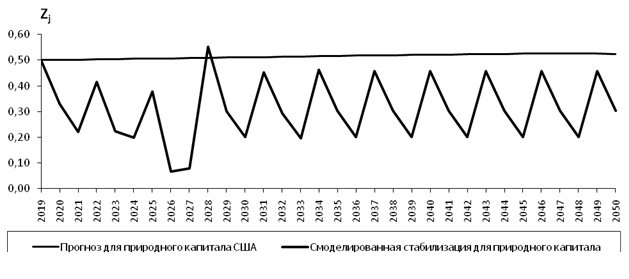
Рисунок 12. Смоделированная стабилизация для природного капитала США

Источник: составлено автором.

Рисунки 10–11 демонстрируют смоделированные процессы по устранению кризисного сценария с последующим восстановлением стабильного долгосрочного роста экономико-демографических показателей. Рисунок 12 показывает, что в результате преодоления кризиса экологическая обстановка стабилизируется в строго определенных рамках, но по-прежнему остается далекой от идеального состояния.

Эффективное подавление кризисной тенденции и последующее формирование устойчивого периодичного тренда обеспечиваются за счет управления, заданного формулой (10).

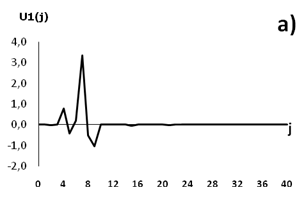
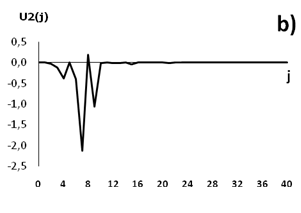
Рисунок 13. Графики функций управления: a) для численности населения; b) для ВВП на душу населения

Источник: составлено автором.

Представленные на рисунке 13 графики показывают, что функции управления имеют импульсообразную форму с быстрозатухающей амплитудой. Отсюда следует, что антикризисные управленческие корректировки имеют точечный характер и должны проводиться в строго определенных размерах и в нужные моменты времени. Рисунок 13 наглядно демонстрирует, что антикризисное управление необходимо осуществлять наиболее активно и регулярно в течение первых десяти лет с начала кризиса. Таким образом, в случае реализации полученного для США прогноза американским властям для преодоления кризиса придется отказаться от части либеральных постулатов в пользу авторитарных методов управления с применением жестких мер в экономических и миграционных процессах.

Заключение

Предложенная в данной статье модифицированная модель Wonderland представляет научный и практический интерес с точки зрения разработки эффективных мер по преодолению экономико-экологических кризисов. На примере статистических данных США смоделирован процесс, когда сначала подавляется кризисная тенденция, а затем формируется устойчивый долгосрочный тренд. Причем этот тренд является периодичным и возрастающим. С помощью формулы (10) моделируются математически формализованные рекомендации по нейтрализации кризиса. Полученные результаты показывают, что существуют эффективные управленческие меры по преодолению кризиса и восстановлению растущей экономико-экологической динамики.

Разработанная формула (10) позволяет рассчитывать точные сроки и размеры управленческих корректировок, необходимых для устранения кризисных сценариев. Это дает возможность для осуществления превентивных мер по упреждению экономико-экологических кризисов. Сконструированная модель (9) – (10) может использоваться в качестве вспомогательного инструмента при разработке антикризисных мер.