Имитационное моделирование микроструктуры фондового рынка на основе высокочастотной и трансакционной информации

Введение

В начале 1990-х годов начало развиваться относительно новое направление экономики, изучающее процессы взаимодействия участников при ценообразовании на финансовые активы. Рыночная микроструктура получила свое название вследствие того, что пытается описать процессы ценообразования, происходящие в краткосрочном периоде на уровне взаимодействия и заключения сделок между участниками [15]. Первые модели рыночной микроструктуры описывали механизмы функционирования дилерского рынка. В процессе своей эволюции структура фондового рынка претерпела серьезные изменения, особенно с переходом современных бирж к электронным торгам. На данный момент большинство бирж функционируют на основе механизма непрерывного двойного аукциона (англ. continuous double auction, CDA). Основной принцип данного механизма торгов заключается в непрерывном взаимодействии покупателей и продавцов на рынке. Данное взаимодействие приводит к возникновению значительного объема высокочастотной информации обо всех событиях в ходе торгов.

Отличительной особенностью рыночной микроструктуры, является использование в исследованиях информации о динамике заявок поступающих в двойной непрерывный аукцион, о процессах отмен заявок и о трансакциях. С развитием современных информационных технологий, использование данной информации становится доступно широкому кругу исследователей для целей конструирования имитационных моделей. Разработка таких моделей позволяет проводить более глубокий анализ деятельности таких сложных социально-экономических систем как фондовый рынок.

Процесс развития фондового рынка и появление систем высокочастотной и алгоритмической торговли привели к существенному усложнению типологии рыночных участников, их стратегий поведения и более сложному взаимодействию между покупателями и продавцами на фондовом рынке. Возросшая сложность взаимодействия негативно сказывается на устойчивости финансовой системы в целом. В свете этого, имитационные модели позволяющие учитывать сложность взаимодействия между покупателями и продавцами, а также реакцию участников на изменения правил торгов становятся все более востребованными.

Большинство созданных имитационных моделей фондового рынка [7, 8] обладают теоретическим подходом [8] к моделированию поведения агентов (семейство моделей «SF-ASM»), отсутствием иерархии участников фондового рынка (модели с «нулевым интеллектом» [9-11]) и моделированием процессов отмен заявок с помощью пуассоновских процессов. Для построения более качественных имитационных моделей и выявления структурных изменений при регулировании фондового рынка, необходимо опираться на эмпирические данные о взаимодействии участников рынка. В настоящее время для моделирования свойств микроструктуры фондового рынка принято использовать модели «с нулевым интеллектом» [12].

Имитационная модель микроструктуры

В ходе исследования нами была разработана принципиально новая модель микроструктуры фондового рынка, которая учитывает внутреннюю иерархию участников торгов. Данная модель сняла ограничения (в том числе отсутствие учета регулирования фондового рынка) семейства моделей «с нулевым интеллектом», которые оказывали негативное влияние на качество и точность имитационной модели [2]. Разработанная модель включает в себя 2 типа агентов: шумовые агенты и высокочастотные участники рынка (см. рис. 1).

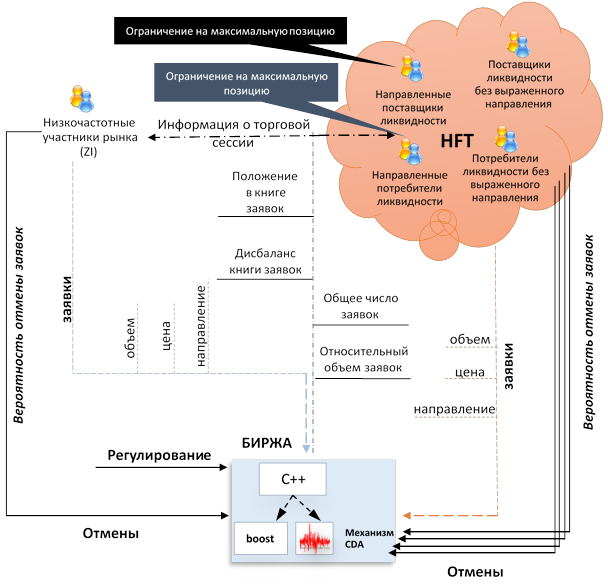
Рис. 1. Схема имитационной модели микроструктуры фондового рынка (составлено автором)

Высокочастотные участники рынка подразделены на 4 типа агентов: направленные поставщики ликвидности (межрыночные арбитражеры), направленные потребители ликвидности (алгоритмы исполняющие крупные заявки), поставщики ликвидности без выраженного направления в торговле (маркет-мейкеры), потребители ликвидности без выраженного направления в торговле (статистические арбитражеры). Каждый из агентов выставляет и снимает заявки на рынке. Каждая выставляемая заявка имеет направление, объем и цену. Мы предлагаем моделировать объем заявок с использованием степенного распределения, которое бы позволяло воссоздавать ситуацию прихода на рынок крупных заявок и приводящих к существенным изменениям на микроструктурном уровне. Для моделирования цены заявки рассматривалось распределение расстояния заявки от лучших цен на рынке. Для каждого из агентов оцениваются параметры распределений заявок и оценивается временная зависимость числа входящих заявок. Каждый участник выставляет отмены своих заявок с заданной вероятностью. Вероятность отмены заявок является условной и зависит от характеристик текущего состояния рынка:

· позиция в книге заявок;

· дисбаланс спроса и предложения;

· относительная величины заявки;

· общее число заявок на рынке.

Для учета изменений параметров потока заявок, в настоящем исследовании для каждого из рассматриваемых финансовых инструментов (более 60 инструментов) были оценены исследуемые параметры и впервые получены зависимости параметров от размера шага цены (тика или минимального изменения цены). Полученные зависимости хорошо соотносятся с наблюдаемыми на практике явлениями и взаимосвязями. В первую очередь существует степенная зависимость между углом наклона в распределении объемов заявок и уровнем шага цены на рынке. Эмпирические наблюдения за поведением рынка, соответствуют обнаруженной закономерности более частого прихода на рынок крупных заявок с большой величиной относительного минимального изменения цены, при это на рынке с малым значением уровня шага цены крупные заявки приходят достаточно редко (см. рис. 2).

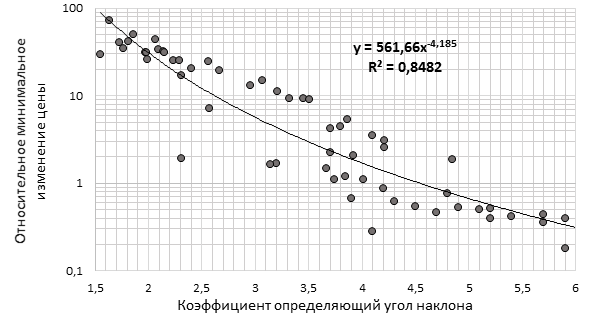
Рис. 2. Диаграмма рассеяния коэффициента наклона степенного распределения от размера относительного тика (составлено автором)

Для учета влияния размера тика на цены приходящих заявок, в ходе исследования впервые [1] было предложено разделить распределение относительных цен заявок на три составных части, для учета влияния размера тика на данное распределение (см. рис. 3).

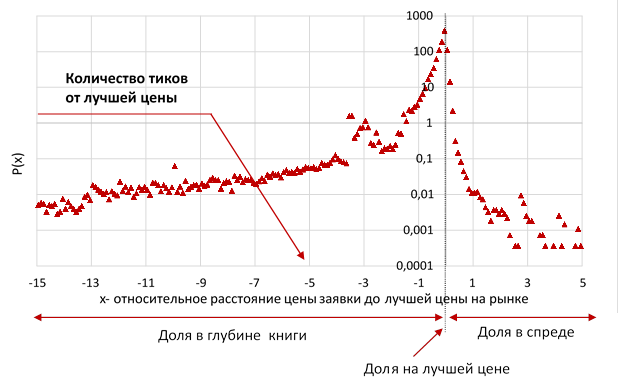
Рис. 3. Распределение расстояния цены заявки от лучших цен на рынке (составлено автором)

Построив данное распределение для более 60 инструментов с различными уровнями тика, для составных частей распределения цен приходящих заявок были обнаружены зависимости от размера тика (см. рис. 4). Данные зависимости объясняют фундаментальные различия в ценах приходящих заявок для финансовых инструментов с малым и большим значением тиков.

Для заявок, приходящих на лучшую цену на рынке, коэффициент наклона положителен. Данный факт свидетельствует о том, что с ростом размера шага цены растет и доля заявок, приходящих на уровень лучшей цены на рынке. Для заявок, попадающих на противоположную сторону книги заявок, угол наклона отрицательный. Таким образом, с увеличением размера тика уменьшается число сделок. Кроме того, нами ранее было обнаружено, что левая часть распределения хорошо описывается логнормальным распределением. Мы построили зависимости среднего и стандартного отклонения логнормального распределения от размера минимального изменения цены на рынке и обнаружили степенные зависимости.

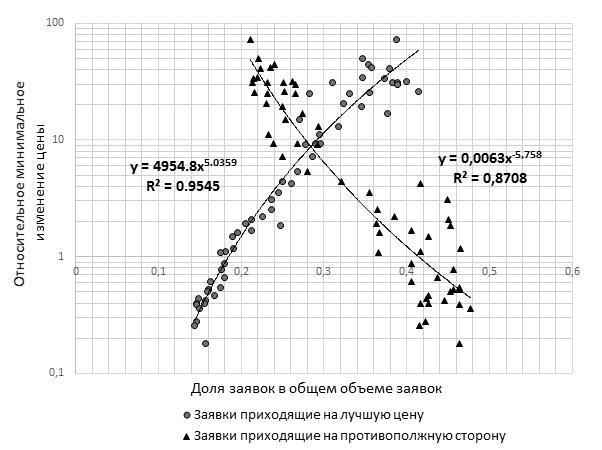
Рис. 4. Диаграмма рассеяния доли приходящих заявок от размера относительного тика (составлено автором)

При увеличении размера тика среднее значение цены приходящих на рынок заявок уменьшается и, таким образом, на рынок начинают приходить заявки близко к лучшим ценам (см. рис. 5). В случае же с уменьшением размера относительного тика среднее распределение увеличивается, что выражается в приходе заявок далеко вглубь биржевого стакана (далеко от лучших цен спроса и предложения).

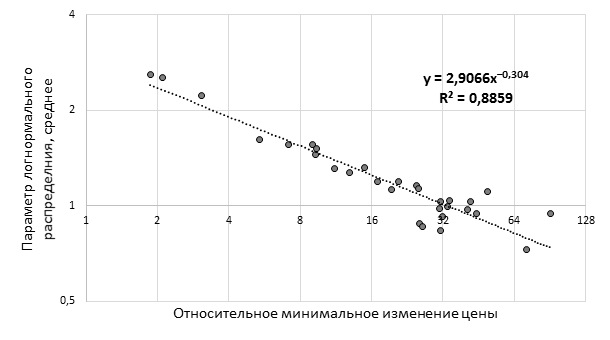
Рис. 5. Диаграмма рассеяния среднего в логнормальном распределении приходящих заявок от размера относительного тика (составлено автором)

Анализируя зависимость стандартного отклонения логнормального распределения от уровня размера тика, можно говорить об обратной зависимости (см. рис. 6). При увеличении размера тика стандартное отклонение уменьшается, что означает консолидирование ликвидности вокруг среднего. В случае же уменьшения размера тика ликвидность становится «размазанной» по стакану, таким образом заполняя больше ценовых уровней.

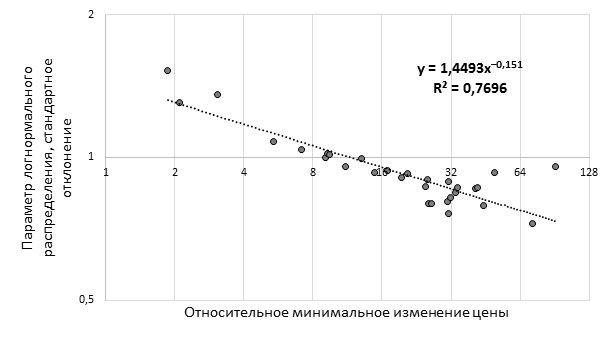
Рис. 6. Диаграмма рассеяния стандартного отклонения в логнормальном распределении приходящих заявок от размера относительного тика (составлено автором)

В данной работе были обнаружены зависимости параметров рынка от размера тика и предложена методика построения имитационных моделей, позволяющая учитывать последствия изменений размера тика в свойствах потока заявок. При оценки зависимостей показателей, была проведена кросс-валидация и выявлена устойчивость в зависимостях. Данная методика может быть выражена следующей системой уравнений:

(1)

K1 – параметр чувствительности вероятности отмены заявки к относительной позиции заявки в книге заявок;

αvolume– угол наклона степенного закона в распределении объемов заявки; – параметр чувствительности вероятности отмены заявки к дисбалансу в книге заявок;

– вероятность попадания заявки внутрь книги заявок (для заявок на покупку цена ниже лучшей цены спроса и для заявок на продажу выше лучшей цены предложения);

– вероятность попадания заявки на противоположную сторону книги заявок (для заявок на покупку цена выше лучшей цены спроса и для заявок на продажу ниже лучшей цены предложения);

– вероятность попадания заявки на лучшую цену (для заявок на покупку цена равна лучшей цене спроса и для заявок на продажу цена равна лучшей цене предложения);

­– величина относительного размера тика на рынке.

В модели также учитывается характер изменения интенсивности потока заявок в зависимости от уровня размера тика. В финансовой практике хорошо известен показатель, называемый среднедневной величиной торгов на рынке (ADTV). Данная характеристика показывает среднее значение объема операций, совершаемых на финансовом рынке по исследуемому инструменту. Она является довольно постоянной во времени. При этом при уменьшении размера тика на рынке средняя величина заявки уменьшается. Данный процесс должен вызывать изменения в интенсивности потока заявок (приводить к увеличению количества приходящих заявок). Для вычисления общего количества приходящих на рынок заявок мы используем следующее выражение:

	(2)
– суммарное количество приходящих заявок; – средний объём заявки, рассчитанный по эмпирическим данным или с использованием аппроксимирующего распределения; – средний объём оборота заявок за день (в количестве акций).

После того как нами было вычислено общее количество заявок, приходящих на рынок, мы корректируем общее количество с учетом внутридневного паттерна. Таким образом, в ходе исследования мы обнаружили, что с уменьшением размера шага цены:

· средний размер заявки на рынке уменьшается;

· количество сделок, происходящих на рынке, увеличивается [6];

· количество заявок, приходящих на уровень лучшей цены на рынке, снижается;

· общая вероятность отмены заявки увеличивается;

· вероятность отмены становится более чувствительной к ситуации на рынке.

Моделирование процесса отмен заявок

Рассмотренная выше модель имитационного моделирования микроструктуры фондового рынка опирается на модель условной вероятности отмены заявок предложенной С. Майком и Д. Фармером [13]. Мы выделили наиболее значимые параметры, которые способы влиять на процесс отмены заявок на финансовом рынке:

· Число заявок находящихся в книге заявок и показывающее суммарную величину спроса и предложения на рынке,

· Относительный объем заявки показывающий степень превышения спроса или предложения на лучших ценах на рынке,

· Дисбаланс спроса и предложения на рынке,

· Относительная позиция заявки в книге заявок, показывающая на сколько далеко заявка отклонилась от текущих рыночных цен,

Для каждой из данных характеристик была построена функция условной вероятности отмены и оценена функциональная форма такой зависимости (см. рис. 7-10) [4]. Для функции условной вероятности отмены в зависимости от числа заявок, функциональная форма отражает факт того, что при определенном уровне наполнения книги заявок, чувствительность вероятности отмены снижается по отношению к дальнейшему наполнению книги.

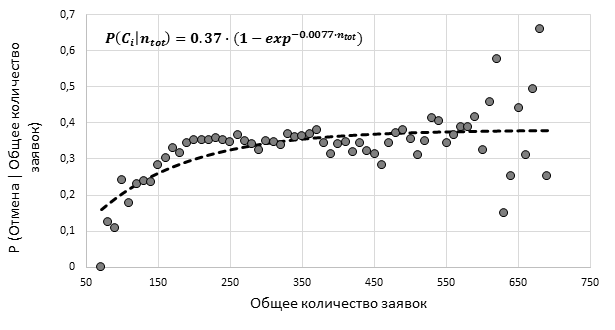
Рис. 7. Функция условной вероятности отмены заявки в зависимости от числа заявок в книге заявок, акции компании Singapore Telecommunications (составлено автором)

Заявки с большим значением относительного объема имеют тенденцию к более частым отменам вследствие невозможности исполнения на рынке. Такого рода зависимости выраженные степенной функцией достаточно часто встречаются на фондовых рынках.

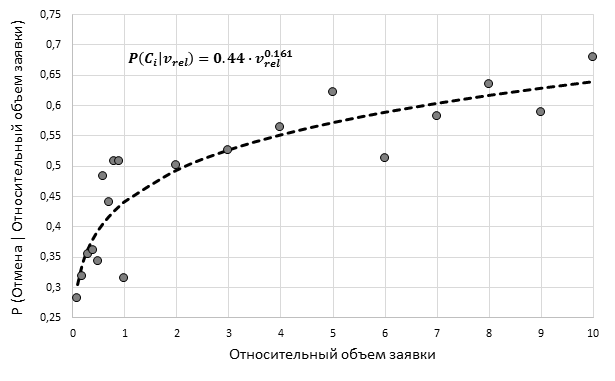
Рис. 8. Функция условной вероятности отмены заявки в зависимости от относительного объема заявки, акции компании Singapore Telecommunications (составлено автором)

Заявки являются достаточно чувствительными к дисбалансу в книге заявок и такого рода зависимости подтверждаются предыдущими исследованиями и реальной практикой участников финансовых рынков.

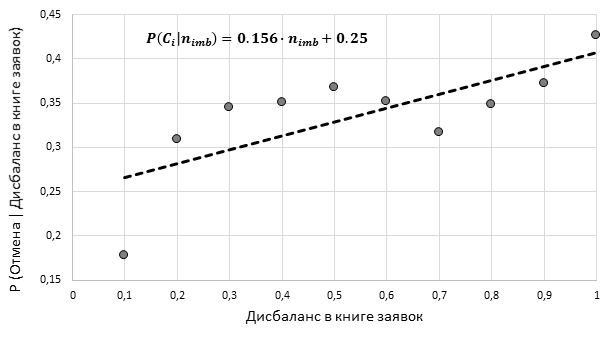
Рис. 9. Функция условной вероятности отмены заявки в зависимости от дисбаланса в книге заявок, акции компании Singapore Telecommunications (составлено автором)

Для функции условной вероятности отмены в зависимости от позиции заявки, функциональная форма отражает факт того, что при отдалении рыночной цены от цены заявки, вероятность отмены значительно вырастает.

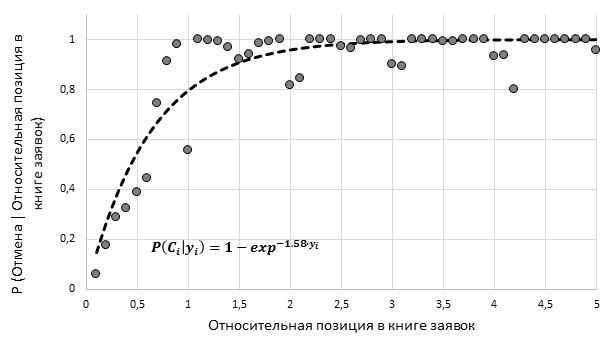
Рис. 10. Функция условной вероятности отмены заявки в зависимости от относительной позиции заявки в книге заявок, акции компании Singapore Telecommunications (составлено автором)

В общем виде формула условной вероятности отмены заявок выглядит следующим образом:

(3)

где:

– условная вероятность отмены заявки,

– относительная позиция заявки в книге заявок,

– коэффициент дисбаланса в книге заявок,

– общее число заявок в книге заявок,

– относительный объем заявки

– параметр, характеризующий максимальную вероятность отмены заявки,

– параметр чувствительности вероятности отмены к относительной позиции заявки в книге заявок,

– параметр чувствительности вероятности отмены к общему числу заявок,

– параметр чувствительности вероятности отмены к дисбалансу в книге заявок,

– параметр поправки коэффициента дисбаланса;

– параметр чувствительности вероятности отмены к относительному объему заявки

При этом процесс отмены заявок в явном виде не зависит от времени, а лишь только от состояния книги заявок. Для параметров и b, участвующих в процессе отмены заявок выявлены зависимости уровня размера тика на конкретном финансовом инструменте. Коэффициент отвечает за чувствительность цены заявки к текущему состоянию рынка. Из выявленной зависимости (см. рис. 11) следует, что с уменьшением размера тика снижается чувствительность цены заявки к текущему положению цены на рынке.

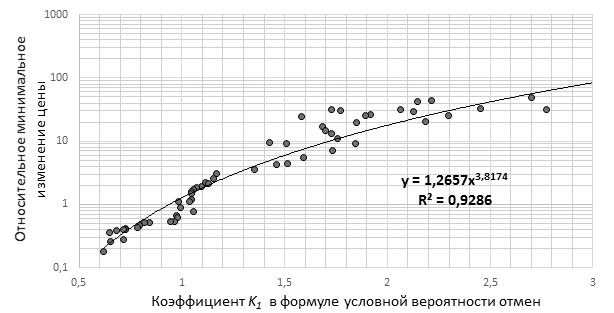
Рис. 11. Диаграмма рассеяния зависимости коэффициента условной вероятности отмен от размера относительного тика (составлено автором)

Кроме того, для низкочастотных участников рынка была обнаружена зависимость от коэффициента (см. рис. 12), который отвечает за восприимчивость участников к дисбалансу в книге заявок. При увеличении размера тика значение данного коэффициента снижается, что может соотноситься с ситуацией, когда участники становятся менее чувствительными к дисбалансу. В то же время при уменьшении размера тика коэффициент увеличивается и чувствительность к дисбалансу в книге заявок растет. При этом необходимо заметить, что, анализируя обе зависимости, можно прийти к выводу о том, что при уменьшении размера тика общая вероятность отмены заявки увеличивается. При увеличении размера тика общая вероятность уменьшается.

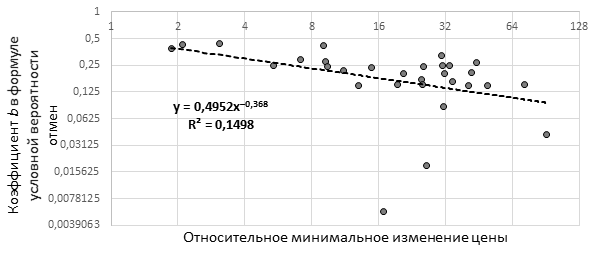
Рис. 12. Диаграмма рассеяния зависимости коэффициента b условной вероятности отмен от размера относительного тика (составлено автором)

Для различных участников торгов проанализированы функции отмены заявок и выделены компоненты не значимые в процессе отмены заявок (так например для HFT участников, которые являются направленными потребителями ликвидности, дисбаланс в книге заявок не значим).

Валидация имитационных моделей

Одним из важнейших этапов построения имитационной модели является процедура оценки качества модели микроструктуры. Предложенная нами процедура состоит из 2 этапов. На первом этапе оцениваются распределения основных характеристик по эмпирическим и имитационным сценариям:

· Приросты

· Объем торгов по сделкам совершенным на рынке

· Число сделок совершенных на рынке

· Величина бид-аск спрэда на рынке

· Показатель волатильности цен на рынке

· Соотношение числа заявок к числу сделок совершенных на рынке

· Показатели ликвидности связанные с сжатостью книги заявок (такие показатели как XLM или RTCI)

· Число заявок находящихся в книге заявок

· Время жизни заявок, выраженное в секундах (пример сравнения распределений)

В случае, когда по данным характеристикам отличия между различными торговыми днями эмпирических сценариев превышают или равны различиям между имитационными и эмпирическими сценариями, тогда можно говорить о достаточно адекватном воспроизведении микроструктуры фондового рынка. Следующим этапом является (на основе принципов Балчи [5]) визуальное сравнение тепловых карт ликвидности рынка из эмпирических и имитационных сценариях (пример см. рис. 13.)

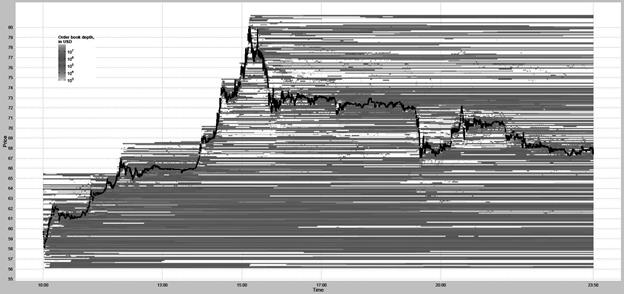
Рис. 13. Сравнение тепловых карт ликвидности рынка (составлено автором)

В случае соответствия статистических характеристик имитационной модели и реального рынка, и уровня ликвидности на этих рынках, требуется дальнейшая проверка на соответствие стилизованным фактам финансового рынка:

· Тяжелые хвосты в приростах цен

· Отсутствие длинной памяти в приростах цен

· Длинная память в абсолютных значениях ценовых приростов

· Кластеризация волатильности

· Корреляция волатильности и объема

· Эффект взаимосвязи объема и волатильности

· Высокий коэффициент эксцесса в ценовых распределениях

Стоит заметить, что данные стилизованные факты могут наблюдаться не на всех финансовых рынках (особенно на рынка с большим значением уровня тика). Таким образом, наличие данных стилизованных фактов не является необходимым условиям для всех рынков, но соответствие наличия/отсутствия между эмпирическими и имитационными моделями, является необходимым условием качественной модели.

После того, как все тесты на соответствие характеристик имитационной модели микроструктуры рынка были пройдены, строятся соответствующие ценовые траектории по каждой из реализаций движения цены и исторические сценарии (или данные вне выборки, out of sample). Визуальное сравнение позволяет удостовериться в адекватности построенной модели.

Программная реализация

На основе предложенных автором экономико-математических подходов, моделей и методов разработан программный комплекс, предоставляющий инструментарий для поддержки принятия управленческих решений в области регулирования правил торгов на фондовом рынке. Программная реализация производилась на объектно-ориентированном языке C++. Для создания пользовательского интерфейса была использована среда разработки Qt – свободное программное обеспечение, позволяющее разрабатывать кросс-платформенные приложения. Разработанный комплекс включает в себя модуль анализа финансовых инструментов, модуль настройки имитационных моделей (см. рис. 14), модуль сравнения сценариев и модуль детального анализа симуляций.

В отличие от существующих аналогов [14], построенный комплекс позволяет оценивать влияние регулирования на взаимодействие участников в процессе ценообразования и проводить процедуру валидации построенных моделей.

В рамках рассматриваемого программного комплекса были построены модели по различным сценариям регулирования фондового рынка. В целях оценки последствий регулирования достаточно часто рассматриваются 3 различных сценария (для инструментов с большим текущим значением тика): (a) снижение размера тика, (b) увеличение HFT активности, (c) cнижение размера тика и увеличение HFT активности. В качестве примера рассмотрим возможное регулирование торгов обыкновенными акциями компании Singapore Telecommunications.

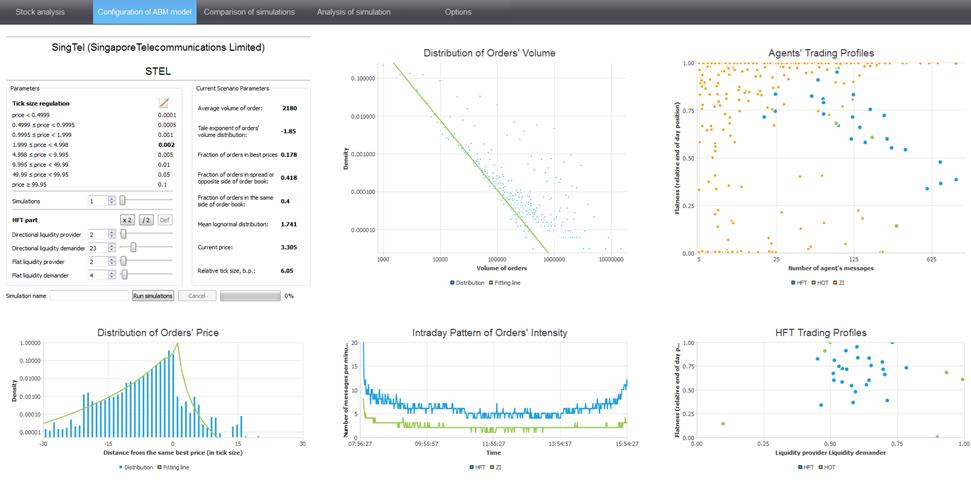
Рис. 14. Пример модуля настройки имитационных моделей микроструктуры фондового рынка, разработанного программного комплекса (составлено автором)

Данный финансовый инструмент имеет большой шаг цены (30 базисных пунктов). В первую очередь рассматривается имитационный сценарий динамики торгов при отсутствии изменений правил проведения торгов (имитационный сценарий). Данный сценарий должен сопоставим по своим количественным и качественным характеристикам с эмпирическими данными. В случае, когда по сравниваемым характеристикам (объем торгов, ликвидность, волатильность и д.р.) отличия между различными торговыми днями эмпирических сценариев превышают или равны различиям между имитационными и эмпирическими сценариями, тогда можно говорить о достаточно адекватном воспроизведении эмпирической микроструктуры фондового рынка. Кроме сравнения средних величин по различным сценариям по отношению к историческим данным, пользователь может проводить сравнительный анализ при помощи усиковой диаграммы, которая позволяет проводить сравнение, при этом не делая никаких предположений относительно распределений, лежащих в основе анализируемых характеристик (см. рис. 15).

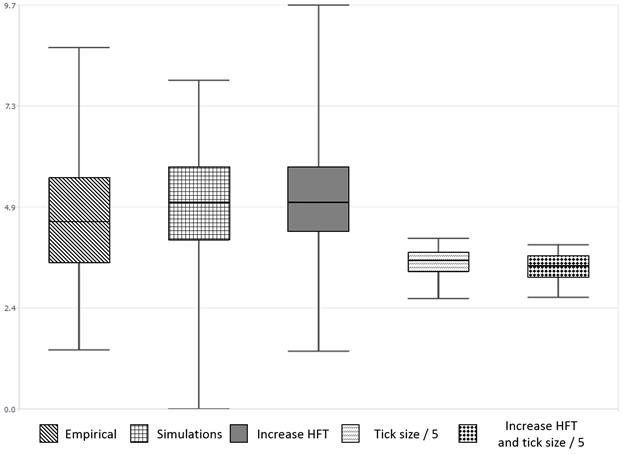
Рис. 15. Усиковая диаграмма волатильности в модуле сравнения сценариев для акций компании Singapore Telecommunications (составлено автором)

Нами были построены усиковые диаграммы для торгового объема, количества сделок и волатильности для всех рассматриваемых выше сценариев. Каждый график содержит в себе (слева направо): исторический сценарий, имитационный сценарий, (a) сценарий увеличения активности HFT, (b) сценарий уменьшения размера тика, (c) комбинацию уменьшения размера тика и увеличения активности HFT. Как видно из рисунка 15, эти сценарии являются довольно схожими как по медианным значениям, так и по дисперсии. В случае увеличения активности HFT волатильность незначительно снижается. Когда происходит снижение размера тика без увеличения активности HFT, волатильность на рынке значительно снижается, при этом, если на рынок приходят HFT, дисперсия волатильности возрастает. Таким образом, наблюдается нелинейная зависимость показателя волатильности в различных сценариях. Подытоживая сценарный анализ моделей, можно говорить о том, что различные сценарии регулирования рынка носят в значительной степени нелинейный характер, но при этом сформулированная система валидации модели позволяет достаточно адекватно оценивать качество построенной имитационной модели и прогнозировать последствия регулирования хода торгов на фондовых рынках (результаты хорошо соотносятся с регулированием на Японском фондовом рынке [3]).

Заключение

В данном исследовании была решена проблема построения имитационных моделей на основе высокочастотных и транзакционных данных которые, в отличие от существующих аналогов, способны учитывать изменения со стороны регулятора финансовых рынков (в области изменения размера тика и в области ограничений или преференций для определенного класса участников рынка). В данной работе получили развитие подходы связанные с моделированием динамики и микроструктуры финансового рынка основываясь на высокочастотных и трансакционных данных. Были изложены подходы к построению имитационного потока заявок, учитывающего стилизованные факты и другие закономерности высокочастотной информации. Предложен способ идентификации и кластеризации агентов на финансовом рынке для построения иерархии участников финансового рынка. Введена процедура валидации, измеряющая степень правдоподобия построенной модели. Разработана и обоснована новая спецификация модели отмены заявок для различных классов агентов, отражающая особенности отмен заявок на финансовых инструментах с различным размером тика. Полученные прикладные результаты позволяют рассматривать их как предпосылку для развития программного комплекса для анализа последствий принимаемых решений в области регулирования, таких как ограничение минимального шага цены, минимального времени жизни заявки, налога на транзакции и других мер, планируемых к применению мировыми финансовыми регуляторами, в том числе в рамках закона Додда-Франка и европейской директивы MiFID II.