Краткосрочное качественное прогнозирование изменений темпов инфляции в странах Евразийского экономического союза на основе применения волновой динамики Эллиотта

Введение

К задачам краткосрочного прогнозирования динамических параметров применимы различные инструменты технического анализа. Мы используем один из них, а именно теорию волновой динамики Ральфа Эллиотта [1] (Elliott, 1938). Инструментарий, разработанный Эллиоттом, хорошо применим в целях выявления так называемой поворотной точки, или точки бифуркации. Из всего инструментария, в основе которого лежат разработанные Р.Н. Эллиоттом принципы волновой теории [2] (Elliott, 1940), нас интересует конкретный инструмент прогнозирования – завершающая диагональ (Ending Diagonal). Она указывает направление дальнейшего протекания волнового процесса на основе анализа динамики временного ряда. Этот инструмент с момента его изобретения широко используется, причем не только в исследовании технических систем, где он впервые возник, но и в экономических и социальных науках, в основном для прогнозирования рядов динамики. Наибольшее распространение он приобрел в задачах исследования краткосрочной динамики рынков ценных бумаг.

Сам Ральф Нельсон Эллиотт настаивал на том, что применяемые им инструменты позволяют любую сложную динамическую систему в известном смысле воспринимать как фрактальную, т.е. диктуемые волновыми принципами закономерности, которые применимы к анализу динамики целой системы, хорошо подходят и для анализа поведения отдельных ее составных частей и наоборот.

Популяризаторами волновой теории Эллиотта в 70-е годы выступили Роберт Пректер и Альфред Фрост [3] (Prekter, Frost, 2012). Они убедительно показали общесистемный характер данной теории, возможность ее применения к исследованию и прогнозированию динамики сложных систем различной природы – не только отраслевых рынков, но и макросистем, причем на разных временных горизонтах, и не только экономических, но и физических, и технических и прочих систем.

В частности, Пректер и Фрост утверждали, что волновая динамика Эллиотта восходит к идее Фибоначчи о золотом сечении, лежащем в основе естественных пропорций элементов сложных динамических систем. Они обсуждали связь волн Эллиотта с длинными циклами (например, с волнами Кондратьева в экономике) и сверхдлинными циклами, динамика которых обусловлена изменениями парадигм политического устройства современных обществ, – в частности, выделяли суперцикл, берущий начало с 1789 года. Также Пректер и Фрост обнаружили связь волновой теории Эллиотта с теорией случайных блужданий – широко известным в науке теоретическим построением, тесно связанным с парадигмой случайного поиска, имеющей многочисленные приложения в современной физике и технических науках.

До нынешнего времени не прекращаются исследования аналогий применения волновой теории Эллиотта в задачах экономики и физики [4] (Gordeev, Lebedeva, 2017). Авторы этих строк на своем исследовательском опыте убедились в том, что принцип завершающей диагонали Эллиотта показал хорошие результаты, например, в задачах прогнозирования распространения коронавируса в России и в отдельных ее регионах (некоторая часть соответствующих результатов представлена в [5] (Goridko, 2020)). Эта задача, как легко понять, не имеет прямого отношения ни к экономике, ни к физике, но эвристический потенциал волновой теории Эллиотта и здесь оказался весьма высоким.

Методология

Смысл принципа завершающей диагонали заключается в том, что на графике временного ряда прямой линией соединяются точки, находящиеся в крайних верхних позициях (так называемые шапки или шляпы), и другой прямой линией – точки, находящиеся в крайних нижних позициях (так называемые подошвы). Если эти две линии расходятся и в ближайшей перспективе не пересекутся, то дальнейшая динамика временного ряда в краткосрочном горизонте сохранится в том направлении, которое указывает текущий тренд. Если же эти две линии сходятся, то динамика в скором времени сменится на противоположную по отношению к текущему тренду.

Глубина временного ряда, на которой обнаружились крайние левые опорные точки линии «шляп» и линии «подошв», покажут горизонт, на котором дальнейшая динамика отчетливо подтвердит направленность текущего тренда (если эти линии разошлись) или однозначно сменит эту направленность на противоположную (если эти линии сходятся). Чем глубже временной ряд, к которому пришлось прибегнуть для построения линий «шляп» и «подошв», тем более отдалена от текущего момента реализация прогноза, касающаяся укрепления или излома текущего тренда.

Как справедливо утверждали Пректер и Фрост, самое трудное в применении волновой теории Эллиотта состоит в том, чтобы отличить тренд от коррекции. В связи с этим можно заметить, что точки, через которые проходят линия «шляп» и линия «подошв», можно выбрать различным образом, но временной горизонт прогноза об изменении или продолжении направленности тренда соответствует временному интервалу между соседними точками, через которые проходит линия «шляп», или между соседними точками, через которые проходит линия «подошв» (как правило, две соседние «шляпы» и две соседние «подошвы» отстоят друг от друга на сопоставимое расстояние).

В качестве примера рассмотрим рисунок 1.

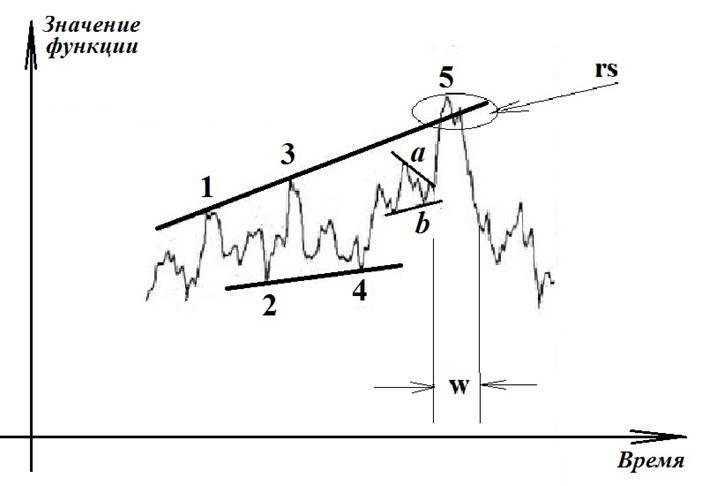
Рисунок 1. Пример краткосрочного прогнозирования динамики временного ряда на основе принципа завершающей диагонали Эллиотта

Источник: составлено авторами.

На данном рисунке, в зависимости от целей прогнозирования, можно провести несколько разных линий «шляп» и «подошв». Если нам интересна ближайшая динамика исследуемого временного ряда, мы проводим линию «шляп» через точки, помеченные цифрами 1 и 3 на рисунке 1, а линию «подошв» – через точки, помеченные цифрами 2 и 4. В этом случае получаем расходящуюся конечную диагональ, т.е. прогнозируем дальнейший подъем значений временного ряда, приходящийся на момент, отстоящий от точки 4 на расстояние, примерно равное расстоянию между точками 2 и 4. Этот подъем на рисунке 1 отмечен цифрой 5 и обведен овалом, отмеченным стрелкой с надписью rs.

Если нам интересна дальнейшая динамика ряда, мы выбираем линии «шляп» и «подошв» несколько правее (соответственно, это линии a и b на рис. 1) и рассматриваем колебания с более высокой частотой. Эти линии сходятся, а это значит, что в динамике временного ряда наступит снижение на расстоянии от последнего основания линий «шляп» и «подошв», примерно равном расстоянию между двумя выбранными «шляпами» или «подошвами». Этот интервал отмечен на рисунке 1 двумя вертикальными прямыми с буквой w между ними. В конце данного интервала, действительно, наблюдается спад значений временного ряда.

За пределами интервала, отмеченного буквой w, видим расходящиеся линии очередных «шляп» и «подошв» при нисходящем тренде, а это значит, что значения рассматриваемого временного ряда и далее продолжат снижение.

Используя описанную методологию, спрогнозируем динамику темпов инфляции в странах ЕАЭС на основании помесячных данных, характеризующих отношение индексов потребительских цен (ИПЦ) каждого месяца к индексам потребительских цен того же месяца предшествующего года. Такой подбор статистических данных (относим март к марту предыдущего года, декабрь к декабрю и т.д.) позволяет не заботиться об исключении сезонности в циклических колебаниях индексов цен и сразу получать качественный результат относительно индекса потребительских цен, выраженного в приращениях по отношению к аналогичному индексу цен годовой давности. Т.е. значение индекса, например, января 2021 года, равное 4, означает, что отношение ИПЦ января 2021 года к ИПЦ января 2020 года составляет 1,04.

Результаты

Перейдем к анализу темпов инфляции по каждой стране ЕАЭС, используя технику завершающей диагонали Эллиотта. За основу берутся данные о темпах инфляции по сентябрь 2022 года включительно, размещаемые на официальных сайтах национальных статистических ведомств и эмиссионных банков соответствующих стран [6–12], и делаются выводы о дальнейшей динамике соответствующих показателей.

Россия

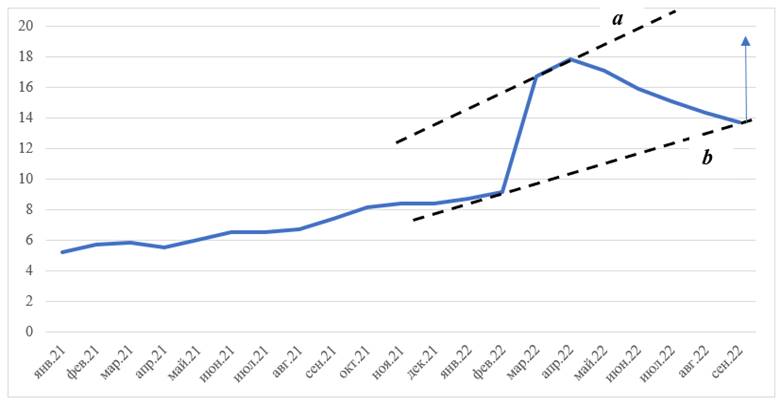
Рисунок 2. Прогнозирование направления изменения инфляции

в Российской Федерации с применением волн Эллиотта

Источник: составлено авторами.

Применим описанные рассуждения к анализу краткосрочной динамики темпов инфляции в российской экономике.

На рисунке 2 мы видим, что линия, соединяющая «шапки» наблюдений (a), растет с большей скоростью, нежели линия, соединяющая «подошвы» (b), при этом эти линии расходятся и в ближайшем будущем не пересекутся. Согласно волновой теории Эллиотта, показатель инфляции находится на повышающей стадии волны и в ближайшее время на ней и останется. Небольшая глубина наблюдений, по которым построены линии «шляп» и «подошв», указывает на то, что полученный прогноз реализуется в самое ближайшее время, т.е. в весьма краткосрочной перспективе (до конца 2022 года) в России следует ожидать роста общего уровня потребительских цен по сравнению с аналогичными показателями годовой давности.

Казахстан

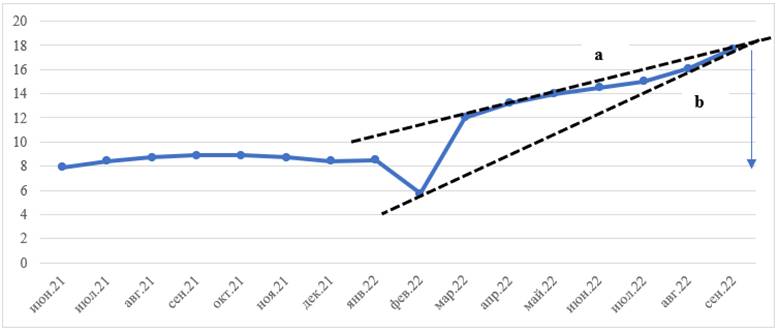
Рисунок 3. Прогнозирование направления изменения инфляции

в Республике Казахстан с применением волн Эллиотта

Источник: составлено авторами.

Аналогично предыдущему волновому анализу Эллиотта, проделанному для темпов инфляции в России, посмотрим на волновую динамику показателей темпов инфляции в Казахстане (рис. 3).

Линия (a), соединяющая «шапки» наблюдений, растет медленнее, нежели линия, соединяющая «подошвы» (b), и эти две линии пересекаются вблизи значений сентября 2022 года. Согласно теории Эллиотта, уже в октябре планируется излом тренда, и ИПЦ перейдет на понижающую траекторию и в ближайшее время на ней и останется. Таким образом, Казахстан в краткосрочной перспективе (как минимум до конца 2022 года) ожидает снижения темпов роста потребительских цен. Это вполне согласуется с фактическим показателем ИПЦ в октябре 2022 г. (см. [6]).

Беларусь

Используя данные [7], мы рассчитали ИПЦ за период с июня 2021 года по сентябрь 2022 года за месяц к месяцу предыдущего года. По этим данным построен график изменения данного показателя на рисунке 4.

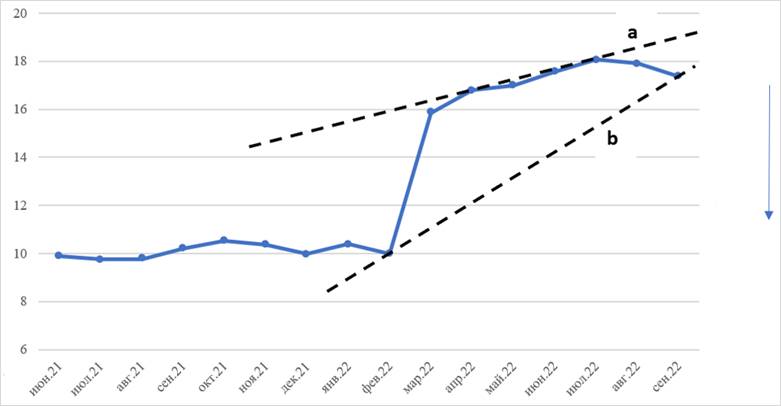
Рисунок 4. Прогнозирование направления изменения инфляции

в Республике Беларусь с применением волн Эллиотта

Источник: составлено авторами.

На рисунке 4 линия (a) растет медленнее, нежели линия (b). Судя по динамике, две линии пересекаются в октябре – ноябре 2022 г., т.е. скорее всего, именно на этот период приходится точка бифуркации, после которой продолжится нисходящая в целом динамика ИПЦ, наблюдаемая на графике начиная с августа 2022 г.

Армения

Информация для проведения волнового анализа инфляции в Армении взята из официального сайта Центрального банка Республики Армения [8]. На ее основании построим график и проведем линии, соединяющие «шапки» и «подошвы» (см. рис. 5).

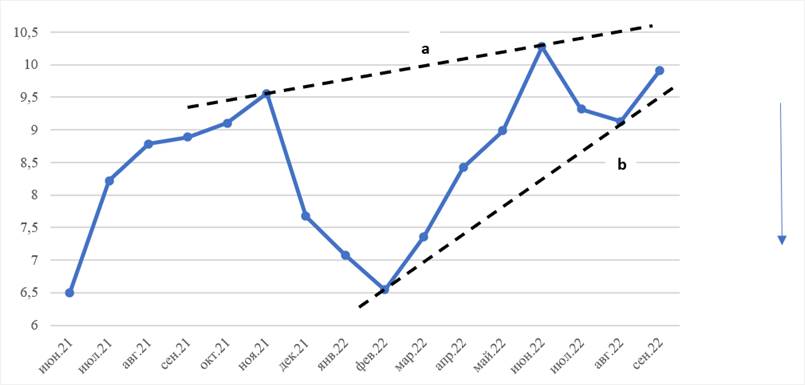Рисунок 5. Прогнозирование направления изменения инфляции

в Армении с применением волн Эллиотта

Источник: составлено авторами.

Итак, для Армении линия (a), соединяющая «шапки» наблюдений, также растет медленнее, нежели линия, соединяющая «подошвы» (b), и эти две линии, скорее всего, пересекутся в первом квартале 2023 года в том случае, если динамика показателя не выйдет за пределы этих линий (a) и (b). Таким образом, по нашему мнению, в феврале – марте 2023 года, согласно теории волновой динамики Эллиотта, состоится излом тренда и темпы роста инфляции начнут снижаться.

Кыргызстан

Данные Национального статистического комитета Кыргызской Республики [9] послужили источником оценки месячной инфляции в стране по отношению к соответствующему месяцу прошлого года. Графически динамику этого показателя (см. рис. 6).

Следовательно, согласно теории Эллиота, Кыргызстан также ожидает снижение темпов роста индекса потребительских цен примерно в ноябре-декабре 2022 года, быть может, несколько позже, учитывая глубину данных временного ряда, используемых для построения линии «подошв».

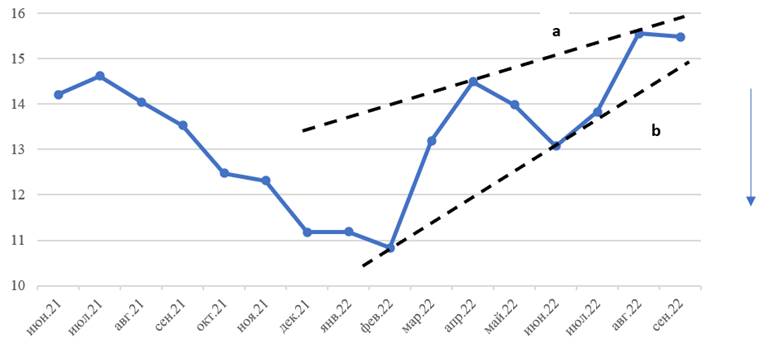Рисунок 6. Прогнозирование направления изменения инфляции

в Кыргызской Республике с применением волн Эллиотта

Источник: составлено авторами.

Заключение

Таким образом, проведенный при помощи волновой динамики Эллиотта анализ динамики индексов потребительских цен стран ЕАЭС показал, что в России отношение помесячных данных ИПЦ к соответствующему показателю годовой давности в краткосрочной перспективе будет возрастать, тогда как в четырех остальных странах ЕАЭС оно будет снижаться. Уже имеющиеся статистические данные за осенние месяцы 2022 года [6–12] отчасти подтвердили сделанные выводы. Об окончательном подтверждении или опровержении сделанного прогноза можно будет судить весной 2023 года, поскольку для большинства рассматриваемых стран прогнозируемые изменения произойдут именно на этом временном горизонте.

Разумеется, «встроенным», имманентным недостатком используемого метода прогнозирования является его качественный характер, не предполагающий получения точных значений индексов цен. Однако для принятия решений в области кредитования и инвестирования проектов в тех или иных отраслях подобной информации качественного характера обычно бывает достаточно.

Более точные прогнозы, содержащие количественные оценки значений индексов цен, могут быть получены, например, при помощи методов регрессионного анализа, в том числе авторегрессии – для тех показателей, динамические ряды которых обнаруживают значимые авторегрессионные зависимости.