Формирование прогнозных оценок расходов на образование в России

Введение

Временной ряд – это последовательность наблюдений, которые делаются обычно через равные промежутки времени. Многие наборы данных отображаются как временные ряды, например: ежемесячное количество товаров, отгруженных с завода; недельный ряд количества дорожно-транспортных происшествий; суточное количество осадков; ежечасные наблюдения на выходе химического процесса и т. д. Примеры временных рядов можно найти в таких областях, как экономика, бизнес, инженерия, естественные науки (особенно геофизика, метеорология), общественные науки.

Под прогнозированием, как правило, понимается процедура предсказания важных показателей для отдельных компаний или фирм. Основные сложности в получении точных прогнозов общих показателей экономической деятельности связаны с неожиданными и важными сдвигами ключевых факторов, например, с изменением внешнеполитической ситуации, результатами выборов, природными катаклизмами. Необходимо отметить, что материалы по выбранной теме превышают все мыслимые объемы: при наборе в поисковой строке словосочетания «Анализ временных рядов» Яндекс выдает 10 млн ответов. Укажем наиболее полные (с точки зрения авторов и, следовательно, субъективно отобранные) источники по данному вопросу [1–4] (Tsay, 2002; Brockwell, Davis, 2002; Chatfield, 2016).

Неотъемлемой чертой ВР является то, что, как правило, смежные наблюдения являются зависимыми. Характер этой зависимости среди наблюдений рядов представляет значительный практический интерес. Анализ временных рядов касается методов изучения этой зависимости, что требует разработки стохастических и динамических моделей для рядов и использования таких моделей в важных областях применения.

Как указано в [1] (Box, Jenkins, Reinsel et al., 2016), первой из пяти важных практических проблем при анализе временных рядов является задача формирования прогнозных оценок. Использование доступных наблюдений за время 𝑡 над рядом с целью прогнозирования его значения на некоторое будущее время 𝑡 + 𝑙 может служить основой для:

· экономического и бизнес-планирования;

· управления запасами и производством;

· планирования производства;

· контроля и оптимизации производственных процессов.

В поставленной задаче предположим, что наблюдения доступны через дискретные равные промежутки времени. Например, в задаче прогнозирования расходов на какой-нибудь вид деятельности расходы 𝑧_𝑡 в текущем месяце 𝑡 и расходы 𝑧_{𝑡 − 1}, 𝑧_{𝑡 − 2}, 𝑧_{𝑡 − 3},… в предыдущие месяцы могут использоваться для формирования оценок прогноза на время 𝑙 = 1, 2, 3,… месяцев вперед. Функцию , которая определяет прогнозы для всех будущих значений 𝑙 на основе доступной информации из текущего и предыдущего значений 𝑧_{𝑡 − 1}, 𝑧_{𝑡 − 2}, 𝑧_{𝑡− 3} через время 𝑡, назовем функцией прогноза. Наша цель – получить такую ​​функцию прогноза, чтобы среднее значение квадрата отклонений 𝑧_{𝑡 +l –} между фактическим и прогнозным значениями было бы настолько мало, насколько это возможно для каждого времени 𝑙.

В такой или сходной постановке обычно ставятся задачи прогноза временных рядов [1–4] (Tsay, 2002; Brockwell, Davis, 2002; Chatfield, 2016), поэтому в данной работе мы только конкретизируем объект исследования и укажем основные шаги ее выполнения. Наблюдаемым временным рядом, показанным на рисунке 1, был ряд расходов на образование в РФ в млрд руб. на протяжении 120 месяцев (десятилетняя помесячная выборка данных с 2010 г. по 2019 г.), который был взят из отчета Росстата [5].

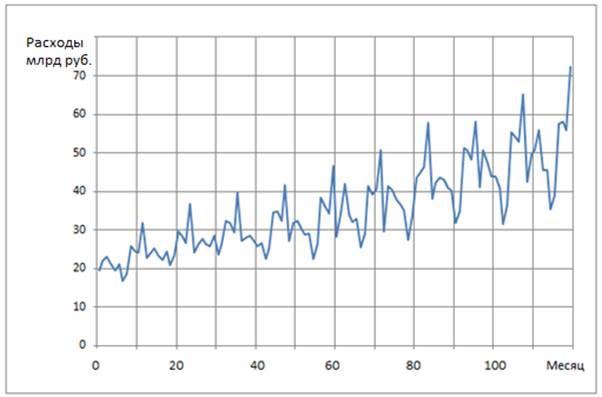
Рисунок 1. Расходы на образование в РФ за 2010–2019 гг.

Источник: составлено авторами по данным [5].

Такой же ряд данных за 2020 г. использовался как тестовый для сопоставления пригодности различных моделей прогноза. Цель статьи заключалась в демонстрации возможностей предложенных моделей с точки зрения достоверности формирования прогноза.

Далее работа структурирована следующим образом. Вначале проводится спектральный анализ ряда, описывается методология проведения исследований, включающая краткое описание используемых моделей, в частности авторегрессионной проинтегрированной модели скользящего среднего (ARIMA), двухслойного персептрона (MLP), динамической нейронной сети (NARNET), сети с долговременной краткосрочной памятью (LSTM). Далее приводятся полученные результаты решения поставленной задачи и анализа найденных оценок. В заключение указываются главные выводы и намечаются пути дальнейшего исследования.

Методология

1. Авторегрессионная проинтегрированная модель скользящего среднего

Аббревиатура ARIMA – autoregressive integrated moving average – авторегрессионная проинтегрированная модель скользящего среднего может использоваться при анализе временных рядов, обладающих нестационарностью и сезонностью. Введение модели ARIMA связано с именами Дж. Бокса и Дж. Дженкинса, которые еще в 70-е годы прошлого века обобщили существующие на тот момент знания в анализе временных рядов, а предложенные ими приемы обработки получили название методологии Бокса-Дженкинса. В 2016 г. вышло уже пятое издание монографии Бокса и Дженкинса, дополненное их последователями [1] (Box, Jenkins, Reinsel et al., 2016).

ARIMA представляет собой класс моделей, объясняющих данный временной ряд на основе его прошлых значений, то есть собственных лагов и запаздывающих ошибок прогноза, так что это уравнение можно использовать для прогнозирования будущих значений. Модель ARIMA (p,d,q) характеризуется тремя показателями: p, d, q, где р – определяет порядок авторегрессионной модели; q – порядок модели скользящего среднего; d – число операций дифференцирования (взятия разностей), необходимое для того, чтобы временной ряд стал стационарным.

Наиболее распространенный способ сделать ряд стационарным – вычесть предыдущее значение из текущего значения. Иногда может потребоваться большее число таких операций, зависящих от сложности ряда. Следовательно, значение d – это минимальная величина разностей, необходимая для трансформации ряда к стационарному виду.

При рассмотрении сезонного временного ряда автокорреляция, соответствующая сезонным лагам (12 наблюдений для месячных данных), значительно отличается от нуля. Такие ряды не моделируются обычными моделями класса ARIMA, потому что высокий порядок (12 или больше) авторегрессионных моделей и/или моделей скользящего среднего приводит к необходимости учета этих корреляций при оценке параметров модели. Не вдаваясь в подробности, о которых можно узнать из приведенных выше источников, отметим, что в этом случае модель преобразуется к виду ARIMA(p,d,q)∙(P,D,Q) , где показатели P,D,Q характеризуют сезонность ряда.

2. Двухслойный персептрон

В качестве следующей модели для построения прогноза воспользуемся схемой двухслойного персептрона, который является традиционным инструментом решения подобных задач. Мы полагаем, что многие знакомы с базовой номенклатурой нейросетей типа многослойных персептронов (multi-layer perceptron – MLP), которые успешно применялись для решения задач прогнозирования в различных областях [6–10] (Khaykin, 2006; Kourentzes, 2013; Hyndman, Athanasopoulos, 2018; Makridakis, Hyndman, Petropoulos, 2019; Januschowski, Gasthaus, 2020). Тем не менее разъясним принцип нейросетевой технологии на однослойной сети с R входами и S нейронами в слое (рис. 2).

В представленной схеме сети каждый элемент входного вектора р соединен с каждым входным нейроном через матрицу весов W. Нейрон с индексом i имеет сумматор, на который поступают взвешенные входы и смещения для формирования i-го скалярного выхода n_i. Различные n_i объединяются вместе, образуя S-й элемент входного вектора n, которые являются аргументами функции активации f. В итоге на выходе сети формируется выходной вектор-столбец а.

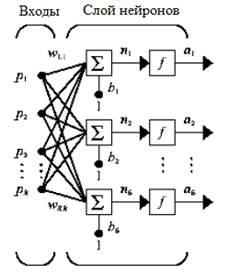
Рисунок 2. Однослойная сеть

Источник: [11].

При формировании прогнозных оценок с помощью MLP обычно используется метод скользящих окон, сущность которого заключается в прохождении системы из двух окон (широкого и узкого) по всей длине анализируемого ряда. Число точек наблюдений, попавших в первое окно, определяет количество нейронов во входном слое персептрона. Значение ряда во втором узком окне (включает только одно наблюдение) дает сигнал учителя. Такая система последовательно проходит по всему ряду, образуя для нейронной сети базу примеров для обучения. Как только узкое окно выйдет за пределы ряда, персептрон будет выдавать прогнозные оценки.

3. Нелинейная авторегрессионная нейронная сеть

Прогнозирование можно считать разновидностью динамической фильтрации, при которой прошлые значения временного ряда используются для определения будущих значений. С учетом нелинейного характера временного ряда можно использовать модели, основанные на нелинейной авторегресии (nonlinear autoregressive – NAR) [12–17] (Chen, Billings, 1989; Domashchenko, Nikulin, 2017; Kin, Sidorenko, Lisakov, Sidorenko, Sypin, 2019; Sabaa, Elsheikhb, 2020). Такая форма прогнозирования может быть записана следующим образом:

z(t) = f [z(t – 1), ..., z(t – d)] + (t),

где d – величина задержки; f – нелинейная функция, которая аппроксимируется в процессе обучения сети путем определения ее оптимальных весов и соответствующего смещения; (t) – случайные ошибки.

Схема сети нелинейной авторегрессии показана на рисунке 3.

Рисунок 3. Сеть нелинейной авторегрессии

Источник: [17] Sabaa, Elsheikhb, 2020).

Нелинейная авторегрессионная нейронная сеть дает особенно хороший прогноз в ситуации, когда временной ряд нелинейный. Сети с временной задержкой похожи на сети с прямой связью за исключением того, что входной вес имеет связанную с ним линию задержки отвода. Это позволяет сети иметь конечный динамический отклик на входные данные временного ряда. Предложенная сеть обучается с использованием алгоритма обучения обратного распространения ошибки Левенберга-Марквардта, который является самым быстрым алгоритмом этого класса.

4. Рекуррентная нейронная сеть

Рекуррентные нейронные сети представляют собой вид нейронных сетей, где связи между элементами образуют направленную последовательность. Благодаря этому появляется возможность обрабатывать серии событий во времени или последовательные пространственные цепочки. Рекуррентная нейронная сеть с ячейкой долговременной краткосрочной памяти (Long short-term memory – LSTM) – особая разновидность архитектуры таких сетей, которая может изучать долгосрочные зависимости между временными шагами последовательности [18, 19] (Ognev, Shchetinin, 2020; Hochreiter, Schmidhuber, 1997). Основными компонентами сети LSTM являются слой ввода последовательности и слой LSTM. Первый слой вводит данные последовательности или временного ряда в сеть. Слой LSTM изучает долгосрочные зависимости между временными шагами данных последовательности.

На рисунке 4 показана архитектура простой сети LSTM для регрессии.

Рисунок 4. Архитектура сети LSTM

Источник: [12].

Сеть начинается с входного слоя, за которым следует слой LSTM. Сеть заканчивается полностью связанным слоем и выходным слоем регрессии.

Архитектура LSTM является наиболее подходящей для моделирования временных связей в глубоких нейронных сетях. Такая архитектура преодолевает проблему исчезающего градиента в РНН для долгосрочного обучения зависимости в данных с использованием ячеек памяти и вентилей.

Сети глубокого обучения первоначально были разработаны для классификации изображений [20] (Gudfellou, Bendzho, Kurvil, 2017). Сеть берет изображение, пропускает его через набор фильтров, применяя весовые коэффициенты к различным аспектам изображения. По существу, здесь работает система отбора признаков, благодаря которой со временем сеть «узнает», какие фильтры аспектов наиболее важны для классификации изображения. Аналогичный метод можно применить и к временным рядам. Хотя временной ряд не имеет физических признаков, как изображение, данные временного ряда содержат пространственные признаки времени.

Ячейка LSTM состоит из нескольких функций вентилей, которые определяют, является ли новая информация важной для задачи прогнозирования и остается ли старая информация актуальной. Такая память называется состоянием ячейки и может хранить всю ранее изученную релевантную информацию для полной обработки последовательности временных рядов. Это позволяет сохранять информацию, полученную намного раньше в последовательности, в ходе полной обработки. В этом состоит основное преимущество архитектуры LSTM перед другими структурами рекуррентных нейронных сетей.

Результаты

Анализ временного ряда

Как видно из рисунка 1, исходный ряд расходов на образование характеризуется наличием ярко выраженных максимумов, которые обусловлены неравномерным финансированием в течение года: в конце каждого года, очевидно, неизрасходованные средства перечисляются на нужды образования. Наш ряд расходов на образование в какой-то степени напоминает классический временной ряд Series G перевозки авиапассажиров аэропорта Лондона с 1949 по 1960 г., который присутствует во многих источниках, начиная с первого издания книги Бокса и Дженкинса [1] (Box, Jenkins, Reinsel et al., 2016).

На рисунке 5 показан спектр анализируемого ряда, указывающий на появление выбросов на определенных частотах.

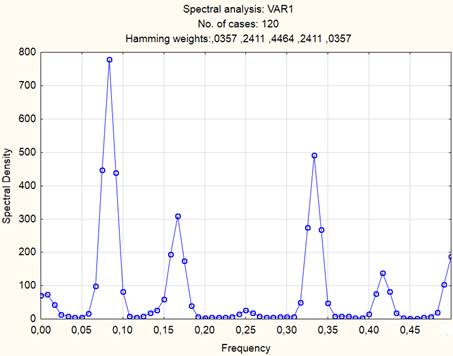
Рисунок 5. Спектральная плотность ряда

Источник: получено авторами.

В таблице 1 приведены значения частот (периодов) появления максимумов.

Таблица 1

Результаты спектрального анализа

Как следует из таблицы 1, самые большие выбросы появляются с периодичностью в 12 месяцев. Кроме того, имеется возрастающий тренд, показывающий увеличение с 2010 по 2019 г. Таким образом, анализируемый ряд расходов на образование является нестационарным (средние значения на различных участках ряда отличаются друг от друга) и сезонным.

Модель ARIMA

Нужно отметить, что идентификация и оценка параметров модели обязательно пересекаются. Также следует пояснить, что идентификация – это всегда неточная процедура. Это объясняется тем, что виды встречающихся на практике моделей зависят от поведения физического мира, поэтому задачу идентификации нельзя решить чисто математическими аргументами.

Для уменьшения амплитуды временного ряда, показанного на рисунке 1, вначале прологарифмируем его, а затем выполним дифференцирование с лагом 1. Преобразованный ряд имеет вид, представленный на рисунке 6, а его автокорреляционная функция (АКФ) показана на рисунке 7.

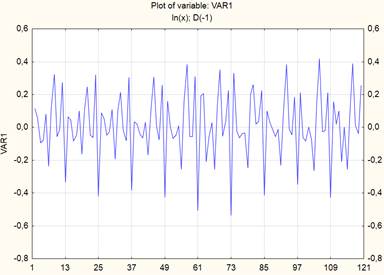
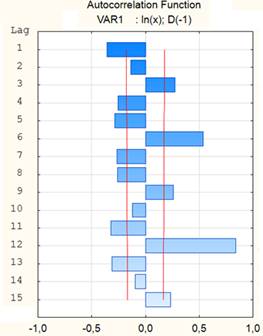
Рисунок 6. Преобразованный ВР

Источник: получено авторами.

Рисунок 7. АКФ ряда

Источник: получено авторами.

Из графика на рисунке 7 следует, что проявляются зависимости высокого порядка (с лагом 12), поэтому дифференцирование с таким лагом должно устранить сезонность. Коррелограммы (здесь не приводятся с целью сокращения) не демонстрируют выбросов, вследствие чего можно приступить к подбору модели. Основываясь на природе ряда, выбираем модель следующего вида: ARIMA (0,1,1)(0,1,1) с сезонностью, определяемой лагом = 12. Таким образом, здесь нужно оценить два параметра модели скользящего среднего: сезонный (Q) и несезонный (q). Никаких параметров авторегрессии в данном случае не оценивается. На рисунке 8 показан график исходного ряда вместе с прогнозом на 12 точек вперед (указаны также доверительные интервалы).

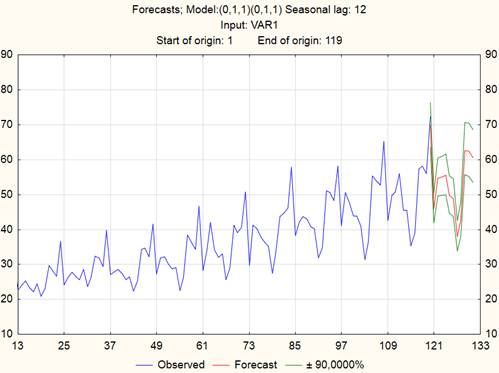
Рисунок 8. Исходный ряд и его прогноз

Источник: получено авторами.

Модель MLP

При использовании двухслойного персептрона его входной слой содержит двенадцать нейронов, соответствующих временному сдвигу. После обучения были выбраны 3 лучших нейронных сети, и их проекции ВР вместе с исходным рядом показаны на рисунке 9.

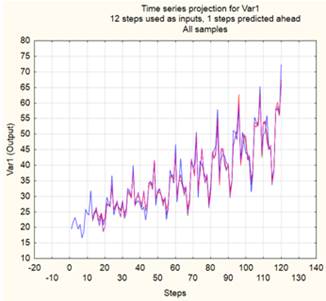
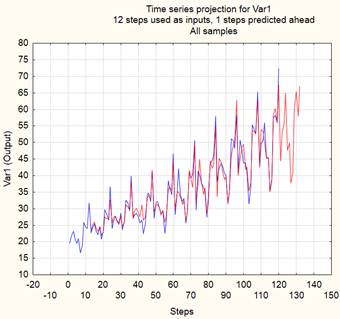
Рисунок 9. Проекции ВР

Источник: получено авторами.

Рисунок 10. Прогноз исходного ряда

Источник: получено авторами.

Как видно из рисунка 9 (приведены 4 кривых), проекции ряда, сформированные тремя нейронными сетями, практически совпадают с исходным рядом. Из трех персептронов был выбран один с такой архитектурой: 12–13–1.

С помощью этой нейронной сети был выполнен прогноз еще на 12 точек вперед, результат которого – на рисунке 10. Как следует из приведенных графиков – исходного ряда и ряда, созданного нейронной сетью, обе кривые практически идентичны на интервале с точки № 13 до точки № 120, поэтому поведение сформированного ряда на интервале точек № 121–132 выглядит правдоподобным.

Модель NAR

При использовании этой модели для обучения сети используется выборка данных, которая делится в следующем соотношении: обучающая выборка – 70%; тестовая выборка – 15%; валидационная выборка – 15%. Обучение нейронной сети производится с помощью алгоритма Левенберга-Маквардта, и архитектура сети показана на рисунке 11.

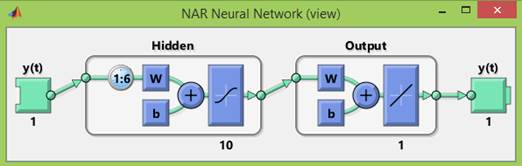
Рисунок 11. Архитектура сети NAR

Источник: получено авторами.

График исходного ряда вместе с кривыми, описывающими деление выборки на три компонента, представлен на рисунке 12.

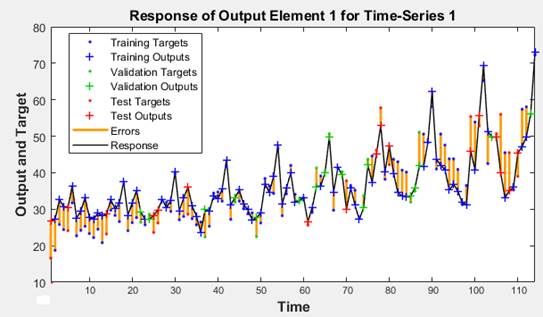
Рисунок 12. Графики полученных рядов

Источник: получено авторами.

Структура созданной сети с обратной связью изображена на рисунке 13.

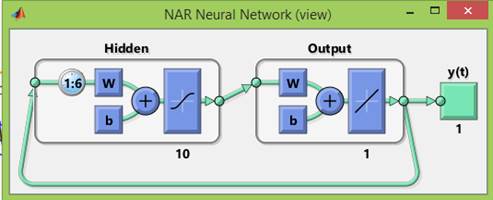
Рисунок 13. Созданная сеть с обратной связью

Источник: получено авторами.

Далее, записав в командном окне Matlab выражение

y2 = netc(cell(0,12),Xic,Aic)

y2 =

1×12 cell array,

получаем прогнозные значения ряда на 12 точек вперед.

Модель LSTM

Эта модель представляет собой разновидность глубокой нейронной сети с такими слоями: последовательность входного слоя; слой LSTM; полностью соединенный слой; слой регрессии. На каждом временном шаге входной последовательности сеть LSTM учится предсказывать значение следующего временного шага. На рисунке 15 показан исходный ряд, спрогнозированный на следующие 12 точек.

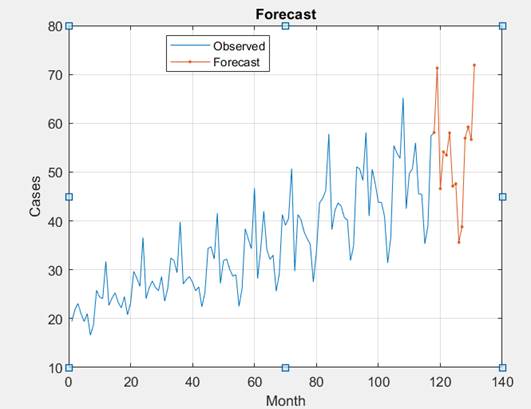
Рисунок 14. Исходный ряд вместе с прогнозными значениями

Источник: получено авторами.

Из рисунка 14 следует, что модель работает вполне достоверно, так как она может точно следовать большинству неожиданных скачков/падений.

В таблице 2 приведены результаты прогноза всех четырех моделей вместе с реальными данными за 2020 г., а на рисунке 15 – соответствующий график.

Таблица 2

Результаты прогноза

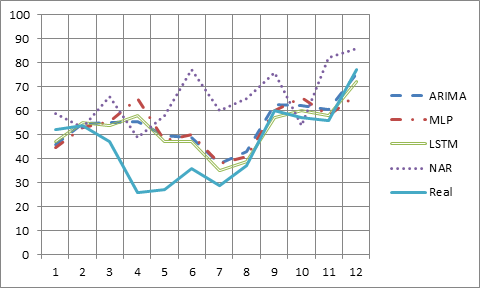
Рисунок 15. График результатов прогноза

Источник: получено авторами.

Обсуждение

Полученные результаты свидетельствуют о том, что несмотря на подобранные модели прогноза, действительность «не подчиняется» найденным правилам прогнозирования. Как видно из рисунка 17, кривая реальных расходов на образование в первой половине 2020 г. отличается от результатов по всем моделям. Очевидно, сказываются эффекты управления экономикой, на которую оказывают влияние различные, трудноучитываемые факторы, например пандемия, перенос сроков ввода крупных значимых объектов, изменение цен на энергоносители и т.п. По мнению авторов, такая ситуация дает предпосылки к использованию принципа Оккамы, гласящего: »Не следует множить сущее без необходимости». В нашем случае, трансформируя к задаче прогноза, может быть, не следует подбирать чересчур сложные модели, а ограничиться, например, опцией Excel «Построение линии тренда», что в среднем даст вполне приемлемые результаты. Однако тот же принцип не запрещает более сложные объяснения тех или иных явлений.

Заключение

Таким образом, в работе продемонстрирована возможность подбора модели прогноза расходов на образование в России. В качестве различных моделей использовались авторегрессионная проинтегрированная модель скользящего среднего (ARIMA), двухслойный персептрон (MLP), динамическая нейронная сеть (NARNET), сеть с долговременной краткосрочной памятью (LSTM). Подбор моделей осуществлялся на 10-летнем периоде наблюдений, а проверка достоверности – на данных следующего года. Анализ результатов показал, что ни одна из моделей не дает точного прогноза вследствие, очевидно, трудноучитываемых внешних факторов.