Байесовский подход в финансовой инженерии: конструируем интеллектуальные системы поддержки финансовых решений

Введение

Реалии цифровой экономики привели к тому, что работодатели, как в корпоративном, так и в государственном секторе, резко увеличили спрос на специалистов, способных применять методы искусственного интеллекта в любой сфере деятельности. Это обусловило актуальность исследований в области методологии и методики преподавания, учитывающих тенденции цифровизации и интеллектуализации экономики. В современных условиях вузам приходится перестраивать учебные программы, особенно в магистратуре, буквально «на ходу». Однако при обучении магистрантов возникла проблема базовой подготовки, которая не могла бы появиться в традиционном специалитете. Эта проблема связана с тем, что, например, в магистратуре по направлениям «Экономика», «Финансы и кредит» и «Менеджмент» может оказаться студент практически с любой базовой подготовкой – инженерной, медицинской или искусствоведческой [1] (Voronov, 2019). Целью работы является обоснование некоторых подходов к решению данной проблемы.

Студенты, которые закончили бакалавриат по экономическим специальностям, обычно имеют хорошую математическую подготовку. Из раздела теории вероятностей они легко вспоминают классические определения, понятия условной и полной вероятности случайного события. У выпускников технических специальностей бакалавриата уровень остаточных знаний по математике, естественно, бывает даже повыше. Однако у гуманитариев такой подготовки может не оказаться совсем. Поэтому, чтобы подойти к такой теме, как, например, «Основы конструирования систем поддержки принятия финансовых решений (СППФР)», приходится делать предварительный опрос студентов. Если опрос покажет, что с базовыми понятиями знакома меньшая часть аудитории, то лектору неизбежно придется как минимум кратко изложить основы классической и байесовской теории вероятностей, иначе двигаться дальше будет бесполезно.

Другим важным моментом является вопрос мотивации. За редким исключением студенты пока еще плохо представляют себе возможности современных компьютерных систем, построенных на базе искусственного интеллекта. Несмотря на имеющийся общий фон цифровизации, они чаще считают, что все это появится в далекой перспективе. Здесь хорошую поддержку дают примеры уже реализованных интеллектуальных систем в нашей предметной области. В финансовой инженерии такие проекты появились еще в 90-х гг. прошлого столетия.

В частности, многокритериальная система поддержки принятия финансовых решений FINEVA (1996 г.) использовалась для анализа финансового состояния греческих транспортных компаний [10] (Zopounidis, Doumpos, 2000). Система HYPER-SAVINGS (1997 г.) была разработана для поддержки решений при формировании инвестиционного портфеля, составленного из различных инвестиционных продуктов, предлагаемых банками [6] (Lee, Nam, 1997). Система FINCLAS (1998 г.) была разработана для поддержки принятия решений при оценке кредитного риска клиентов. С помощью этой системы анализировался баланс, отчет о прибылях и убытках и несколько нефинансовых показателей компании за пять лет. На выходе аналитического блока система рассчитывала около тридцати коэффициентов, характеризующих финансовое состояние компании, кредитную, инвестиционную и дивидендную политику. Графический блок также выдавал эти показатели в динамике за пять лет.

Позднее, в 2000-х гг. появилось множество новых, не менее интересных разработок в этой сфере. Например, в 2011 г. была представлена система IPSSIS (Integrated Portfolio Synthesis and Selection Information System). Система создавалась для формирования портфелей и отбора ценных бумаг с учетом многомерности природы фондового рынка. В качестве особенности системы была заявлена возможность для лица, принимающего портфельные решения (ЛПР), реализовывать свои индивидуальные предпочтения. Система была апробирована на фондовой бирже Афин [8] (Xidonas, Mavrotas, Zopounidis, Psarras, 2011).

В последнем десятилетии спектр задач СППФР расширился, а их уровень сложности возрос. В дополнение к классическим задачам корпоративных финансов появились проекты в таких областях, как торговля финансовыми инструментами, анализ системных рисков, доверительное управление, финансовая безопасность и противостояние мошенничеству [9] (Zopounidis, Doumpos, Niklis, 2018). В частности, в 2015 г. было опубликовано описание системы BankSealer. При обучении эта система строит модель поведенческой динамики расходов каждого клиента банка на основании истории всех его предыдущих операций. Затем она анализирует текущие операции клиента и выявляет аномалии по сравнению с привычной динамикой расходов с целью своевременного предупреждения менеджеров банка [5] (Carminati, Caron, Maggi, Epifani, Zanero, 2015).

Наш опыт показывает, что независимо от уровня подготовленности студентов в начале разделов, посвященных задачам машинного обучения, требуется сопоставление экономического и вероятностного содержания понятий «ожидаемая доходность» и «волатильность» (стандартное отклонение). Если речь идет о магистратуре, то в рамках курса «Финансовое конструирование» мы традиционно рассматриваем ожидаемую доходность как доходность, ожидаемую инвесторами (или иными экономическими агентами) с учетом восприятия рисков. С этой точки зрения полезно акцентировать внимание аудитории на том, что в вероятностном подходе доходность всегда рассматривается как случайная величина и является аналогом математического ожидания в классической теории вероятностей, откуда и идет само название термина «ожидаемая доходность». В полном соответствии с таким подходом мы можем рассматривать волатильность величины доходности любого финансового инструмента (актива) как стандартное отклонение [1] (Voronov, 2019).

После того как студенты успешно усваивают переход к простым вероятностным аналогам, наступает момент для перехода к понятию неопределенности, затрудняющей классические вероятностные подходы к решению множества экономических и финансовых задач. По нашему мнению, этот переход следует начинать с источников неопределенностей, которых оказывается довольно много, в частности это могут быть:

- неполнота информации об экономических объектах наблюдений;

- неточность полученных данных и информации, их возможная неоднозначность, противоречивость, а зачастую и просто отсутствие;

- субъективность экспертных оценок;

- незнание или косвенные, опосредованные знания о скрытых рыночных процессах, объектах и связях между ними;

- лингвистические неопределенности, связанные с обобщенными определениями, например, такими как быстрый рост процентных ставок, высокая ценовая волатильность и т. д.

Отметим, что многие источники неопределенностей в экономике непонятны настолько, что объяснить их природу студентам не всегда представляется возможным. Но сам этот факт облегчает переход к последующему объяснению необходимости использования экспертных систем, предназначенных для работы в условиях неопределенностей. Именно здесь студентам дается первое определение экспертной системы как специализированной компьютерной программы, или программно-аппаратного комплекса, который позволяет выгодно использовать главные преимущества машинных алгоритмов: высокую точность вычислений и быстроту перебора огромного количества вариантов решений, сравнений, недоступную для человека.

Основным отличием любой экспертной системы от обычной программы для ЭВМ является наличие базы знаний о предметной области. Такая база знаний формируется вместе с самой системой, накапливается и совершенствуется в процессе ее полного жизненного цикла. Для того чтобы наглядно показать студентам, как это происходит, лучше всего вместе с ними сконструировать и построить прямо в рамках курса собственную, пусть и небольшую, упрощенную экспертную систему. Если система будет построена в терминах изучаемой предметной области, например финансовой инженерии, то все дидактические и иные задачи курса будут успешно решены. Опыт показывает, что запуск и апробация в ходе занятий такой экспертной системы являются важнейшим условием качественного и полного усвоения темы и всегда воспринимаются аудиторией с большим энтузиазмом.

В рамках семестрового курса финансовой инженерии студенты получают достаточно полное представление об основных видах первичных и производных финансовых инструментов и стратегиях их использования. Поэтому к завершению курса, когда и запланировано изучение возможностей экспертных систем, они уже способны рассуждать о вероятностных состояниях переменных, характеризующих параметры конкретных инструментов, исходя из логики текущего состояния финансового рынка. Студентам предлагается разработать и построить действующую логико-вероятностную модель поддержки принятия решения инвестора по одному из таких инструментов.

Модель строится в программной среде Netica (Norsys), в которой состояние узлов переменных байесовской сети очень наглядно визуализируется на горизонтальных стержневых диаграммах вероятностей [7]. Для того чтобы задать в таблицах безусловные (маржинальные) и условные вероятности априорного состояния узлов сети, студенты могут адаптировать любые заключения экспертов, роль которых могут играть, в том числе они сами и преподаватель. Рассуждения экспертов берутся за основу при первоначальном обучении и инициализации байесовской модели. Далее априорные состояния узлов могут легко корректироваться на любом этапе конструирования и использования модели, что является большим преимуществом всех байесовских сетей доверия (БСД) [4] (Tulupev, Nikolenko, Sirotkin, 2006).

Обычно для начального заполнения таблиц вероятностей принимаются некоторые предварительные гипотезы о текущем состоянии рынка и возможных реакциях переменных, включенных в модель, на его изменения. Как это происходит, мы покажем на примере простой байесовской сетевой модели для анализа решений об исполнении европейского опциона колл на акцию [2] (Voronov, 2021). Сеть состоит всего из 2 узлов (см. рис. 1):

- узел Рrice (P) описывает состояние случайной переменной текущей цены акции;

- узел Decision (D) отображает варианты решения об исполнении опциона.

Узел Р является родительским, поэтому таблицу безусловных вероятностей (ТБВ, таблица 1) его состояния заполняем исходя из того, что инвестору как лицу, принимающему решения (ЛПР), известно состояние рынка. Допустим, что основываясь на собственном опыте, с вероятностью 60% он ожидает, что цена Р акции будет расти и превысит цену исполнения Х опциона. Он также считает, что вероятность точного совпадения цен Р и Х очень низка (10%), поэтому оставшиеся 30% составляют вероятность того, что цена Р акции окажется ниже цены исполнения Х.

Таблица 1

ТБВ для узла Р

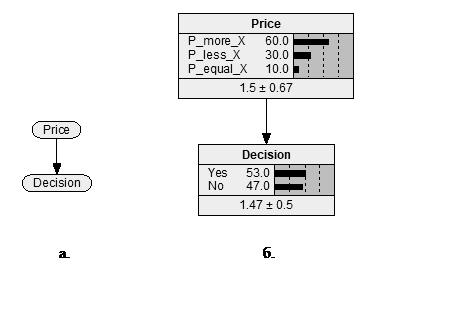
Рисунок 1. Байесовская сетевая модель задачи: схема графа (а) и стержневые диаграммы вероятностей (б), построенные с помощью программы Netica

Источник: составлено авторами.

Таблицу условных вероятностей (ТУВ) для узла D начнем заполнять исходя из того, что исполнение опциона выгодно инвестору только в том случае, если цена Р акции превысит цену исполнения опциона Х (табл. 2, 1-я строка). Однако при этом не следует забывать, что если это превышение будет незначительным, то оно не покроет премию, которую инвестор уже уплатил продавцу опциона. Таким образом, уверенность в исполнении опциона может в этом случае быть равна не 100%, а например, 80%.

Таблица 2

ТУВ для узла D

Если P < X (2-я строка ТУВ), то исполнение невыгодно инвестору всегда, поэтому отказу от исполнения присваиваем 100% вероятность. Если Р точно равно Х (3-я строка ТУВ), то инвестору практически безразлично – исполнять или не исполнять опцион, поскольку и то и другое дает одинаковый экономический результат. В терминах вероятности такое состояние обычно записывают как 50/50.

Отметим, что до начала инициализации модели программа выводит на стержневых диаграммах лишь предварительные значения равных вероятностей. После заполнения всех таблиц инициализируем построенную БСД и сразу получаем на стержневой диаграмме верхнего узла распределение маржинальных вероятностей, а в нижнем узле – распределение полных вероятностей в исходном состоянии модели до поступления каких-либо свидетельств (рис. 1б). При подстановке значений вероятностей из таблиц 1 и 2 для проверки машины действительно получаем (в долях единицы):

D yes = 0,8 · 0,6 + 0 · 0,3 + 0,5 · 0,1 = 0,53;

D no = 0,2 · 0,6 + 1 · 0,3 + 0,5 · 0,1 = 0,47.

Полученные результаты говорят о том, что модель работает и ее можно использовать для вероятностных выводов. Как известно, байесовские модели подобного типа позволяют делать вероятностные выводы как в прямом (диагностика), так и в обратном (прогнозирование) направлениях.

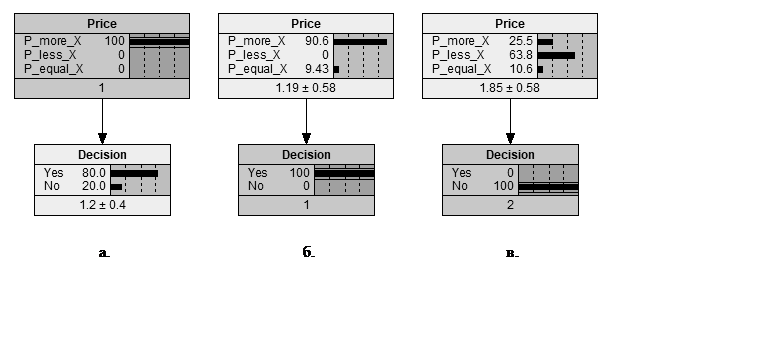
Рисунок 2. Результаты вероятностных выводов

Источник: составлено авторами.

В графическом интерфейсе программы Netica выводами и состояниями можно управлять простым кликом по соответствующему стержню любой диаграммы. При этом имитируется реализация соответствующего события (вводится свидетельство), а вероятности на связанных узлах автоматически и почти мгновенно пересчитываются и выводятся на их диаграммах [3] (Toropova, 2016).

На рисунке 2а в качестве примера прямого вывода показано состояние сети в случае реализации случайного события P > X. После этого в узле вариантов решений значения полных вероятностей изменились и соответствуют 80% вероятности исполнения нашего опциона. На рисунке 2б показано одно из состояний обратного вывода, которое показывает, что если опцион исполняется, то с вероятностью 90,6% (но не 100%) цена акции превысила цену исполнения, но при этом все же остается 9,43% вероятности того, что цена акции будет равна цене исполнения. Самый интересный вывод следует из рисунка 2в. Он говорит о том, что отказ от исполнения опциона в построенной модели может произойти с вероятностью 63,8%, при этом отказ вероятен на 25,5%, даже если цена акции превысит цену исполнения, и на 10,6% при равенстве цен!

Для проверки полученных результатов, используя те же табличные данные, найдем вручную апостериорные вероятности состояния цены акции при условии, что опцион был исполнен (рис. 2б). Для этого вспомним формулу теоремы Байеса и подставим в нее все, что у нас есть:

;

;

,

здесь: P(P_m|D_yes) – апостериорная вероятность того, что цена акции превысит цену исполнения опциона при условии, что опцион исполняется;

P(P_l|D_yes) – апостериорная вероятность того, что цена акции окажется ниже цены исполнения опциона при условии, что опцион исполняется;

P(P_e|D_yes) – апостериорная вероятность того, что цена акции будет равна цене исполнения опциона при условии, что опцион исполняется;

P(D_yes|P_m) – вероятность того, что опцион будет исполнен при условии, если цена акции превысит цену исполнения опциона;

P(P_m) – априорная вероятность того, что цена акции превысит цену исполнения опциона;

P(D_yes) – полная вероятность исполнения опциона.

Как видим, результаты наших расчетов (с учетом округлений) полностью соответствуют результатам, полученным машиной.

Визуализация процесса обучения модели в данной программной среде, на наш взгляд, очень удачна. Если в учебной аудитории имеется локальная компьютерная сеть или хотя бы экранный проектор, то обсуждение заключений экспертов и само обучение модели не оставляет равнодушным никого – в нем обычно с интересом участвует вся группа.

В дальнейшем построенная модель легко переносится на любой компьютер. Она позволяет практически мгновенно делать любые корректировки условных и маржинальных вероятностей, добавлять новые узлы (переменные), новые связи. При этом непрерывно накапливается и с каждой новой версией улучшается база знаний, которая и составляет ядро созданной экспертной системы.

Заключение

В заключение отметим, что трехлетний опыт преподавания в изложенном ключе подтвердил наши ожидания. А именно, байесовский подход в сочетании с удачным программным продуктом воспринимается студентами с большим интересом. Возможность построить небольшую экспертную систему прямо на занятии не оставляет равнодушным никого. Разработки, начатые на занятиях, студенты уносят на ноутбуках домой, продолжают экспериментировать, консультироваться, используют их в курсовых и выпускных работах. За прошедшее время на нескольких потоках курса были разработаны подобные системы СППФР:

- о покупке обыкновенной акции;

- о выборе между покупкой акции и размещением денег на банковском депозите;

- о выборе между покупкой акции и покупкой европейского опциона колл на эту же акцию;

- о выборе между покупкой крупного пакета акций и покупкой европейского опциона колл на эти же акции;

- об исполнении реального опциона на продолжение или отказ от производства высокотехнологичного изделия (в разных периодах);

- о выборе между формированием синтетической позиции по акции и покупкой стандартного трехмесячного опциона на колл на эту же акцию;

- о выборе между покупкой акции и формированием синтетической позиции по этой же акции;

- о выборе между покупкой шестимесячного форвардного контракта на акцию и формированием синтетической позиции, аналогичной такому же форварду.

Кроме этого, было разработано несколько простых систем для поддержки корпоративных финансовых решений. По мнению авторов, предложенный подход позволяет не только ликвидировать пробелы в базовой подготовке магистрантов, но и дать им хорошее представление о возможностях использования методов машинного обучения в дальнейшей практической деятельности.