Построение упрощенных моделей цепей поставок для разработки антирисковых стратегических решений

Начиная с 2006 г. руководство Калужской области в качестве пути как экономического, так и инновационного развития, избрало для себя путь развития за счет привлечения в регион прямых инвестиций, преимущественно иностранных.

На первом этапе регион разработал эффективную на тот момент инвестиционную стратегию, суть которой заключалась в обеспечении прямых инвесторов всеми необходимыми ресурсами, инфраструктурой и льготами. На наш взгляд, этот этап был реализован успешно, и в Калужской области был создан ряд иностранных отверточных сборок. Вторым этапом новые производства должны были повысить степень локализации. Этот этап был завершен – иностранные производители повысили степень локализации. Однако инвесторы предпочли привлекать импортных поставщиков для своих производств, таких как «Магна», «ЯПП», «Бентелер», «Вистеон» и другие. Это позволило им поддерживать качество своей продукции на уровне внутренних стандартов. В конечном итоге это привело к формированию закрытого кластера с точки зрения формирования добавленной стоимости и диффузии инноваций.

Главной причиной сложившейся ситуации является то, что калужские поставщики автокомпонентов по ряду причин предлагают продукцию не соответствующего качества и не способны обеспечить стабильных поставок. Не более 5% поставщиков автокомплектующих в России способны обеспечивать поставки продукции на уровне мировых стандартов качества. Если средний показатель дефективности по ISO 16959 не превышает 70 единиц на миллион деталей массового производства, то у российских производителей 1000 единиц (ГОСТ Р 51814.1 – 2009).

Измерения информативности компонентов цепи поставок

В данной статье рассматривается проблема выявления наиболее информативных компонентов цепи для ее упрощения в целях разработки оптимального портфеля антирисковых стратегических мероприятий, направленных на минимизацию экономических потерь в цепи, вызванных отказами и другими нежелательными событиями.

Самая простая цепь состоит из поставщика и потребителя, более сложные цепи имеют разветвленную структуру, в которой могут быть выделены отдельные подсистемы и логистические, технологические связи между ними. Подсистемы могут выделяться с различной глубиной и степенью детализации. Для решения задачи минимизации рисков и повышения качества цепи поставок в целом разработана процедура, позволяющая лаконично представить структуру и выделить те ее подсистемы, которые содержат наиболее полную информацию о факторах риска и связанных с ними экономических потерях. Такой подход позволяет существенно уменьшить объем анализируемых данных о цепи и упростить процедуры принятия решений.

Таким образом, мы предлагаем уменьшить размерность модели, опираясь на измерение степени информативности отдельных ее подсистем. Основная проблема заключается в том, чтобы дать адекватную меру информативности, отражающую количество информации о рисках и связанных с ними потерь и отобрать наиболее существенные и информационно полезные компоненты рассматриваемой цепи.

Различные способы измерения информативности узлов в графах и сетях рассматриваются в (Kasneci et al., 2009; Kireyev, 2009). Как указано в (Battini, Persona, 2007), один из наиболее перспективных аналитических подходов к измерению сложности цепей поставок и производственных систем основан на измерении Шенноновской энтропии (Shannon, 1948).

Для группы событий E = {e1, ..., en} с априорными вероятностями возникновения событий P = {p1, ..., pn}, pi > 0, таких, что pi + … + pn = 1, функция энтропии H определяется следующим образом:

H = – åi pi log pi . (1)

Главная идея заключается в том, что возникновение событий с вероятностью близкой к 0,5 связано с больше неопределенностью, чем событий с более высокой или низкой вероятностью возникновения. Чем неопределенность ниже, тем меньше требуется информации для предсказания события и наоборот. Рост энтропии свидетельствует о росте неопределенности.

Шенноновская энтропия

Шенноновская энтропия успешно применяется для измерения информативности в сложных производственных системах. Например Карп и Ронен (Karp, Ronen, 1992) применяют Шенноновскую энтропию, чтобы показать, что переход к более мелким партиям в производстве может привести к снижению информационных затрат при планировании. Фризел и Вудкок (Frizelle, Woodcock, 1994) делают вывод, что высокая сложность производственной системы, оцениваемая энтропией, препятствует эффективной реализации производственного процесса. Энтропия для оценки уровня сложности систем, в том числе и цепей поставок, и измерения степени неполноты знаний об их состоянии используется в работах (Дулесов, Агеева, 2011; Arteta, Giachetti, 2004; Blecker et al., 2005; Efstathiou et al., 2002; Isik, 2010; Martinez-Olvera, 2008; Sivadasan et al., 2002; Sundar, Lakshminarayanan, 2008). Мы рассматриваем энтропию как меру информативности для анализа и в дальнейшем упрощения модели цепей поставок.

Иерархия цепи поставок в данной статье рассматривается как многослойная структура (см. рис.).

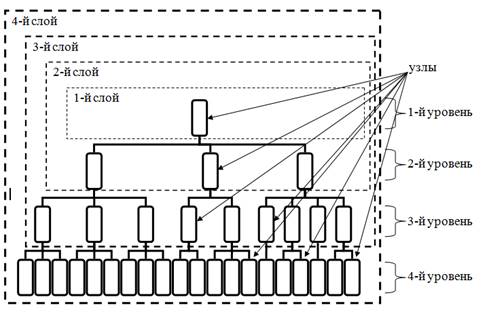
Рис. Узлы, уровни и слои сети поставок

Самый верхний слой содержит несколько основных узлов цепи, которые далее называются «родительскими»: поставщики, автопроизводитель, дилеры, покупатели, каждый из которых может быть детализирован и содержать свою иерархию поставщиков. Будем называть структуру цепи поставок v-усеченной, если она представлена слоем v, т.е. содержит родительские узлы цепи и дочерние узлы от уровня 1 до уровня v. Каждый слой – это последовательное приближенное представление одной и той же цепи поставок, и чем больше значение v, тем более подробно слой с номером v представляет структуру исходной цепи.

Если при переходе от модели, содержащий слой v, к модели с большим значением, т.е. (v + 1), мера информативности изменяется незначительно, такая дальнейшая детализация цепи поставок не имеет смысла. Таким образом, мы будем определять самые информативные компоненты цепи, содержащие достаточно полную информацию для формирования оптимального портфеля стратегических действий.

Для каждого узла v цепи мы формируем информационную базу данных. Эти данные записаны в виде таблицы 1, представляющей собой список событий в узле в течение определенного периода времени (например, месяц). Каждая строка таблицы 1 содержит описание ситуации, а именно события, произошедшего в данном узле цепи поставки в течение выбранной единицы времени (например, в течение дня). Строки информируют, привело ли событие к экономической потере или нет.

Таблица 1

Список событий дочернего узла

В ячейках таблицы 1 записываются значения xrf , равные 0 или 1. Величина (xrf) на пересечении столбца f и строки r равна 1, если фактор f, соответствующий столбцу f, проявился в событии, описанном строкой r, и 0 – в противном случае. Последний столбец таблицы 1 (c номером F + 1) используется для отображения результата события r, а именно: xr,F+1 = 1, если в узле произошел сбой, приведший к экономической потере, a xr,F+1 = 0 означает, что, несмотря на проявление фактора риска, заметной экономической потери не произошло. Пусть число событий, которые привели к сбоям и экономическим потерям всей системы, равно W, такие события мы будем называть критическими.

После того, как мы построим таблицу D для всех узлов, входящих в какой-то произвольный слой, например, v. Для всего слоя v также можно сформировать подобную таблицу 2, объединив списки рисковых событий, входящих в слой узлов.

Таблица 2

Список критических событий слоя 1 (родительского узла U0)

При этом следует исключить влияние строк для узлов с теми рисковыми событиями, которые вызваны их дочерними узлами и уже один раз учтены в данном слое. Если в родительском узле произошло событие, сопровождающееся риском и вызванное сбоем в дочернем узле, то в объединенной таблице 1 в соответствующей строке родительского узла в последнем столбце F + 1 значение 1 меняется на 0, а само рисковое событие учитывается записью 1 в столбце F + 1 соответствующей строки дочернего узла. Если в слой включено bv узлов, то общее число строк в таблице Sv = bvR.

Для каждого f (f = 1, …, F) мы можем вычислить Nv(f) – общее число тех строк в списке событий v-усеченной структуры, для которых в столбце F + 1 стоят xr,F+1 = 1. Относительная частота pv(f|1) случаев, когда фактор f стал причиной экономических потерь, понимается нами как оценка вероятности соответствующего события и определяется для всего списка как:

pv(f|1) = Nv(f) / Nv, (2)

где Nv – общее число строк со значением 1 в последнем столбце F + 1; åf pv(f|1) = 1.

Таблица 3

Относительная частота pv(f|1) случаев, когда фактор f стал причиной

экономических потерь для слоя 3

Одно из свойств функции энтропии состоит в том, что если система разделяется на несколько подсистем, то общая энтропия определяется как взвешенная сумма энтропий подсистем (Karp, Ronen, 1992). Это обстоятельство будем отображать через отношение количества критических событий всей системы W к числу строк Sv в таблице для слоя v.

Мера информативности также должна учитывать размер экономических потерь. Обозначим L – объем потерь, вызванных критическими событиями (это потери в цепи слоя 1). Общий объем всех потерь в цепи может превышать эту величину, но сбой в каком-либо узле может не привести к сбою в следующем по цепи узле и к экономической потере. Это объясняется, например, наличием страховых запасов, либо наличием двух параллельных узлов, когда сбой в одном из них компенсируется деятельностью другого. Иными словами, потери на выходе системы в целом меньше потерь внутри системы. Каждый уровень v цепи поставок вносит свой «вклад» Lv в общий объем потерь L; они суммируются из потерь соответствующих слою уровней (от 1 до v). Соответственно, при анализе v-усеченной структуры цепи имеется информация о потерях, доля которых в сумме потерь, вызванных критическими событиями, составляет Lv/L. Доля потерь нижеследующих слоев (1 – Lv/L); эта величина с ростом v снижается. Чем больше становится номер слоя v, тем больше имеется информации о весе просмотренных уровней цепи в общем объеме критических потерь, а неопределенность в отношении «послойной структуры» размера экономических потерь уменьшается.

Тогда энтропия v-усеченной структуры для рассматриваемой цепи поставок («энтропия слоя v») определяется как:

H (v) = – (1 – Lv/L) (W/Sv) åf pv(f|1) log pv(f|1). (3)

При переходе к следующему слою, т.е. с возрастанием детализации структуры цепи, энтропия снижается. Дальнейшая детализация цепи нецелесообразна, когда это снижение становится незначительным при переходе к последующему слою, т.е. когда:

(H (v – 1) – H (v)) / (H (1) – H (v) ) < e, (4)

где e – пороговое значение относительного изменения энтропии.

v-усеченную структуру, энтропия которой удовлетворяет условию (1), будем называть e‑приближенной. Информация о наиболее значимых факторах риска и соответствующих экономических потерях достаточна для выбора оптимального набора предотвращающих риск стратегий с учетом стоимости и экономического воздействия каждой стратегии при заданном ограничении бюджета.

Основной результат. Так как число критических событий в системе известно (и не зависит от числа слоев), то энтропия H(v) v-усеченной структуры монотонно уменьшается с ростом v и асимптотически приближается к 0 при достаточно больших значенияx v.

Этот результат следует из того факта, что величина (1 – Lv/L) монотонно уменьшается при росте v; величина (W/Sv) также монотонно уменьшается при росте v; а значение åf pv(f|1) log pv(f|1) ограничено сверху величиной log F. Так как параметры задачи, входящие в формулы (1)–(2), известны, легко определить число слоев v*, обеспечивающих требуемое приближение исходной цепи поставок с заранее заданным значением e = e0.

Выводы

1. В рационально организованном процессе принятия стратегических решений менеджеры стремятся избегать излишних подробностей и не используют информацию о внутренних процессах нижних уровней иерархии объекта управления. С одной стороны, необходимо обеспечить достаточный объем информации для правильных, т.е. не приводящих к ущербу, решений, с другой стороны, – минимизировать затраты на получение и обработку этой информации.

2. Предложенная процедура дает эффективный подход к упрощению структуры модели цепи поставок, сокращению ее размерности без потери информативности данных о сбоях и отказах, их причинах и экономических последствиях и может применяться для целей формирования портфеля стратегических решений по повышению устойчивости собственных цепей поставок.