Модели экономической стратегии инновационного поведения фирм

Продолжение. Начало в № 12/2000.

В статье “Киты” инновационной стратегии”, или инновационные аспекты развития российского рынка автомобильных масел, опубликованной в прошлом номере журнала, было показано, что сегодня на отечественном рынке автомобильных масел сложилась олигополистическая структура рынка, т.е. такая рыночная ситуация, когда имеется ограниченное число крупных фирм-участников, занимающихся данным видом бизнеса.

Было показано, что использование индекса Херфиндаля-Хиршмана (HHI), который с 1982 года служит основным ориентиром при осуществлении антимонопольной политики США, позволяет определить не только численность продавцов, но неравенство их положения на рынке. Продолжим наш разговор и приведем несложные вычисления с использованием известных моделей, показывающие насколько неравенство издержек фирм-конкурентов приводит к различному уровню занятия ими рыночной доли в данном сегменте рынка.

Часть 2.

Для анализа рынка с олигополистической конкуренцией существует экономико-математический инструментарий, одной из составляющих которого является построение моделей стратегического поведения фирм. Выбор данного вида моделей разнообразен и варьируется от самых простых, базирующихся на многочисленных упрощающих построение предпосылках, до сложных, требующих использования мощного математического аппарата и позволяющих более точно прогнозировать поведение конкурента. Рассмотрим модели Курно и Штакельберга [2, 4], основывающиеся на ряде таких предпосылок, в зависимости от реалистичности которых, данные модели более или менее корректно описывают реальную ситуацию.

Модель Курно.

Построим модель дуополии Курно, исходя из данных, представленных в табл. 1 (см. № 12/2000). Введем следующую систему предпосылок:

а) существуют только две фирмы на рынке;

б) вход на рынок для других фирм эффективно закрыт;

в) целью деятельности фирм является максимизация прибыли;

г) однородность товара;

д) не существует сговора;

е) фирмы могут предсказать объем выпуска конкурента.

Предположим, что в отрасли существуют только два завода, причем спрос на продукцию ими полностью удовлетворяется. В качестве примера возьмем выпуск (Q) и издержки (AC) за 1999г. следующих заводов (табл. 4).

Таблица 4

Исходные данные для расчета модели Курно

Завод	Q ‑Производство (тонн)	AC (тыс. руб./тонн.)
АО “Ангарская НК”	2000	7810,45
АО "Новокуйбышевский НПЗ"	6900	5260,21

Как правило, при построении данной модели вводится предпосылка о равенстве издержек фирм. В нашем же случае осуществлено моделирование с учетом неравенства издержек.

Пусть функция общих издержек имеет линейный вид:

TC₁=c₁q₁ и TC₂=c₂q₂ ,

причем с₁=AC₁, а c₂=AC₂.

Тогда выручка предприятий будет выражаться следующей формулой:

TR₁=Pq₁, TR₂=Pq₂,

где P_(q)- обратная функция спроса и P_(q)= a ‑ bQ, очевидно, что Q=q₁+q₂.

Тогда:

П₁= TR₁-TC₁= Pq₁-c₁q₁ =(a-b(q₁+q₂)q₁- c₁q₁;

П₂= TR₂-TC₂= Pq₂-c₂q₂ =(a-b(q₁+q₂)q₂- c₂q₂;

Найдем прибылемаксимизирующие количества, приравняв первые частные производные к нулю:

dП₁\dq₁= a-c₁- 2bq₁-bq₂=0 (1)

dП₂\dq₂= a-c₂- 2bq₂-bq₁=0 (2)

Заметим, что в первом уравнении независимой переменной является q₁, в то время, как q₂ рассматривается в качестве константы (уже заданной величины), поэтому, используя ,например, метод подстановки при решении этой системы, из (1) выражаем q₁ как q₁(a, c₁, q₂); подставляем в (2) и получаем q₂ как q₂(a, c₁, c₂). Аналогичные рассуждения справедливы и для второго уравнения.

Итак, получим:

q₁^*= (a - 2c₁+ c₂)/3b (3)

q₂^*= (a - 2c₂+ c₁)/3b (4)

Теперь вернемся к исходным данным (табл. 1). Очевидно, что количество масел, производящееся заводами, есть q₁^* и q₂^*, а АС, указанные в табл. 4, ‑ с₁ ис₂. Подставив эти данные, получим систему из двух линейных уравнений с двумя неизвестными:

6900= (a - 2*5260+7810,45)/3b (5)

2000= (а - 2*7810,45+5260)/3b (6)

Из этих двух уравнений находим значение параметров а и b:

а= 13483,9; b=0,5205.

Из уравнений (1) и (2) получим кривые реагирования R₁(q₂) и R₂(q₁). Получим: R₁ = q₁= (a-c₁)/2b- q₂/2, R₂ = q₂= (a-c₂)/2b- q₁/2. Подставив полученные значения a и b, имеем: R₁=q₁= 7900 ‑ q₂/2, R₂ = q₂ = 5450 ‑ q₁/2. На основе приведенных данных построены кривые реакции дуополистов:

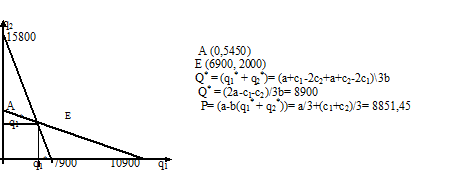
Рис.1. Кривые реакции дуополистов.

Из данных, представленных на рис. 1, следует, что совокупный выпуск в отрасли при данных начальных условиях получается равным 8900 тонн в год, при этом выпущенный товар будет продаваться по цене 8851,45 тыс. руб. Прибыли компаний можно легко подсчитать, подставив в формулу прибыли (П₁ и П₂) значения количества, цену и издержки. Если вернуться к уравнениям (3) и (4), можно заметить, что издержки конкурентов входят в него с положительным знаком, а собственные издержки предприятия - с отрицательным. Таким образом, математически подтвержден вывод о том, что большие издержки конкурентов способствуют увеличению выпуска (в данном случае, рыночной доли) для данной отрасли.

Модель Штакельберга.

В предыдущей модели предполагалось, что оба дуополиста исходят из предположения, что соперник не изменит выпуска в ответ на его собственное решение. Эта предпосылка сильно упрощает модель.

В модели Штакельберга учитывается, что один из дуополистов (лидер) признает право другого на ответный ход, а последователь придерживается предположений Курно: он следует своей кривой реагирования и принимает решения о прибылемаксимизирующем выпуске, полагая выпуск соперника заданным. Предпосылки предыдущей модели о линейности спроса, недифференцированности товара и др. остаются.

В соответствии с теорией экономического анализа [1-4], фирма-лидер должна действовать следующим образом:

1. Лидер, как правило бывает настолько осведомлен, что знает функцию издержек последователя и функцию рыночного спроса. Таким образом, в начале он максимизирует прибыли последователя:

П_f= TR_f ‑TC_f

2. Учитывая предпосылку о линейности спроса, получаем:

П_f = P(Q)q_f ‑ TC_f = P(q_l+q_f) ‑ TC_f.

Для максимизации прибыли, приравниваем первую производную по выпуску последователя к 0 (необходимое, но не достаточное условие): dП_f\dq_f= 0. После чего находим выпуск последователя как функцию от выпуска лидера и инкорпорируем его в собственную функцию прибыли.

3. П_l= F(q_l, R(q_l)). Требуя выполнения вышеупомянутого условия максимизации прибыли, находим значение выпуска лидера, затем, подставляя найденное значение, находим выпуск последователя.

На практике так и происходит. Сначала лидер определяет величину своего выпуска, затем ‑ последователи.

Применим эту модель к имеющимся данным.

Предположим, что лидер ‑ НК “ЛУКойл”, последователь ‑ АО “Ангарская НК”. Сведения о количестве и издержках вынесем отдельно в табл. 5.

Таблица 5

Исходные данные для расчета модели Штакельберга

Завод	Q ‑ Производство (тыс. тонн)	AC (тыс. руб./тонн.)
АО "ЛУКойл-Пермнефтеоргсинтез	230,9	5143
АО “Ангарская НК”	2	7810,45

Далее осуществляем процедуру расчета:

1. П _f=P(Q)q_f -TC_f = P(q_l+q_f) ‑ TC_f. (1)

П_f = (a ‑ b(q₁+q_f))q_f ‑ 7810q_f. (2)

Дифференцируем эту функцию по q_f и получаем:

dП_f\dq_f= a ‑ bq₁ ‑ 2bq_f –7810 = 0 (3)

Из этого уравнения выводим функцию количества последователя:

q_f(q_l)= (a ‑ bq_l ‑ 7810)/2b (4)

2. Теперь подставим (4) в функцию прибыли лидера:

П₁= P(q₁+f(q₁))q₁ ‑ TC₁. (5)

П₁= (a ‑ b(q_l + (a ‑ bq₁ ‑ 7810)/2b)q₁ ‑ 5143q₁. (6)

dП₁\dq₁= a/2 ‑ bq₁+3 905-5 143=0 (7)

Таким образом,

q^*_l= (a/2 ‑ 1238)/b (8)

q^*_f=(a – 7810 ‑ (a/2 ‑ 1238))/2b (9)

3. Подставим данные, приведенные в табл. 2, в систему уравнений (8) и (9) и решим уравнение относительно a и b:

230,9b = a/2 - 1238

4b= a/2-6572

Из данной системы уравнений получены коэффициенты для функции спроса:

a= 6572,3;

b= 0,042.

Подчеркнем еще раз, что в приведенных моделях заданным фактором являлась функция издержек предприятия. Снизить издержки, а значит изменить функцию, позволяет разработка и продвижение на рынок новых продуктов в рамках реализации эффективной инновационной стратегии.

Методическая оценка эффективной инновационной стратегии для нефтяной отрасли была разработана ОАО “ЛУКойл” [5], рассмотренное в данной статье в качестве лидера на российском рынке автомобильных масел.

Таким образом, основными принципами оценки эффективности инновационных мероприятий будут:

единый методический подход к оценке вариантов решения научно-технических проблем компании и многокритериальность оценки;

моделирование потока продукции, ресурсов и денежных средств;

учет альтернативных издержек;

определение эффекта как превышения предстоящих стоимостных интегральных результатов над соответствующими им затратами за весь срок осуществления мероприятия;

учет экономической неравноценности осуществляемых затрат и получаемых результатов в различные моменты времени;

учет инфляции, неопределенности и рисков, оказывающих влияние на принятие решений;

оценка эффективности инноваций с позиций нефтяной компании (ее подразделений) и с позиций национальной экономики;

применение при оценке и отборе инновационных мероприятий для финансирования неформальных процедур отбора.

Определение эффективности инноваций осуществляется на всех этапах их создания и использования, т.е. НИОКР и изготовление (включая подготовку производства новых технических средств и использование их потребителем). База для сравнения инноваций выбирается в зависимости от стадии инновационного процесса и предназначения расчета эффективности.

На стадии НИОКР базой для сравнения служит лучшая по своим параметрам техника (технологический процесс), спроектированная или осваиваемая в РФ или за рубежом. На стадии промышленного производства и использования новой техники (технологии) при оценке планируемого или фактического эффекта в качестве базы сравнения принимается замещаемая техника (технология). При этом, если новшество применяется несколькими подразделениями компании, целесообразно проводить расчеты с использованием в каждом случае индивидуальной базы сравнения. Эффективность инновационного мероприятия определяется на основе его сравнения по затратам и результатам, то есть по "приростным" величинам оценочных показателей.

Реализация приведенных в методике НИЦ ОАО “ЛУКойл” принципов позволяет снизить издержки производства, а также создать дополнительные барьеры, препятствующие входу в отрасль новых фирм и укрепляющие положение существующих в соответствии с выводами и расчетами, полученными в настоящей работе.

Приведенные выше модели описывают лишь один из возможных способов формирования экономической стратегии дуополистов. Тем не менее, существуют и другие способы ценообразования, базирующиеся на менее жестких предпосылках.