Методологические инновации в экономической науке

Введение

Сформировавшийся в настоящее время институциональный вакуум в современной экономической науке обусловлен ограниченностью применяемых методологических подходов и инструментария, носящих традиционный характер, что, несомненно, тормозит развитие экономической мысли.

Вместе с тем отдельные исследователи успешно разрабатывают и талантливо используют новые научные подходы и парадигмы. К их числу относятся трансдисциплинарные подходы, которые применяются в современных научных исследованиях крайне редко, а применительно к теоретическим экономическим исследованиям фактически не используются. Авторы поставили цель раскрыть содержание, специфику и потенциал трансдисциплинарных подходов, которые могут быть применены в различных направлениях экономического анализа.

Термин «трансдисциплинарность» впервые был предложен в 1970 г. швейцарским психологом и философом Ж. Пиаже в дискуссиях с Э. Янчем и А. Личнеровицем в рамках международной рабочей группы «Интердисциплинарность – обучение и исследовательские программы в университетах» [1]. Дальнейшие исследования, в частности Т. Ремадиера, исходили из понимания того, что «…мультидисциплинарность и междисциплинарность не нарушают дисциплинарное мышление. …В случае мультидисциплинарности целью является преимущественно наложение теоретических моделей разных дисциплин. …Междисциплинарность отличается от мультидисциплинарности тем, что конструирует общую модель для вовлеченных дисциплин, основываясь на диалоге между дисциплинами» [2, с. 433–434]. Р. Лоуренс исследовал результаты ее теоретической экспликации и раскрыл их в трех взаимосвязанных перспективах: переоценке представлений о гносеологической ценности знания, новых представлениях о субъекте познания и предпосылках формирования теорий [3, с. 488–489]. Бельгийский ученый Э. Джадж выделил в современной науке четыре вида трансдисциплинарности [4].

В отечественной науке проблемой трансдисциплинарности занимается ряд ученых, например, Л.П. Киященко и В.И. Моисеев [5], рассматривающие генезис и современность трансдисциплинарных исследований. Проблема трансдисциплинарных подходов занимаются ученые Мокий М.С. и Мокий В.С. [6]. Трансдисциплинарную парадигму инноватики разрабатывают Е.Г. Гребенщикова и П.Д. Тищенко [7, 8]. Авторы данной статьи имеют публикации по данной проблеме [9, 10].

Появление новых подходов в современной науке и, прежде всего, в экономической теории обусловлено рядом причин объективного порядка:

- нарастающий вакуум в существующих методологических подходах, как общенаучных, так и частных, специфических для конкретного направления экономической науки (например, институционализма), которые начали формироваться еще в рамках учений А. Смита и Д. Риккардо, дополнены марксистской и неоклассической школами, но до сих пор весьма традиционны и фактически законсервированы;

- в современном экономическом пространстве происходит многократное усложнение различных процессов и явлений, их взаимосвязей, что, несомненно, проецируется на цели и задачи настоящих и будущих исследований и требует методологических подходов более высокого уровня.

Выделим три основные проблемы в методологии:

1. Расширение и обновление категориального аппарата, поток новых терминов, заимствованных из других наук (патология, гены, мутация, вакуум).

2. Новые направления исследования – эконофизика, квантовая экономика, дарвиновская экономика (Р. Фрэнк), экономика счастья.

3. Формирование новой методологии экономической науки (уход от методологического плюрализма к дуализму и методологическому монизму).

Важнейшим методологическим принципом эволюционной экономики является принцип методологического монизма. Это представление о том, что и естественные, и общественные науки должны опираться на единую методологию. В отличие от «методологического дуализма», согласно которому общественные науки не могут использовать методологию естественных наук. В настоящий момент принцип методологического монизма развит настолько, что в среде экономистов все больше зреет убеждение в том, что экономика является, скорее, естественной наукой, чем гуманитарной.

Опора на единую методологию обосновывается следующими соображениями.

Во-первых, классическая экономика, используя за последние десятилетия имеющиеся в ее распоряжении частные методы, не смогла ни предвидеть, ни объяснить развитие реальной экономической ситуации. Об этом свидетельствуют события, связанные с последним экономическим кризисом 2008–2010 гг., пролонгированным в 2014–2016 гг.

Во-вторых, выдающиеся научные результаты получают на стыке наук, поэтому следует не допускать самоизоляции экономической науки, одновременно способствуя интеграции наук и развитию смежных дисциплин.

В-третьих, изучая экономические системы, мы имеем дело со сложными развивающимися динамическими системами, поэтому вынуждены обращаться к методам естественных наук, поскольку ими накоплен богатый опыт построения и исследования подобных систем.

Применение конкретной методологии в научном исследовании принципиально, поскольку предопределяет результативность, успех или, наоборот, фиаско в решении конкретных проблем.

Отметим, что по степени полноты познания окружающего мира как критерия классификации научных подходов выделяют 4 основных вида: дисциплинарный подход, междисциплинарный подход, мультидисциплинарный (полидисциплинарный) подход и трансдисциплинарный системный подход. Дисциплинарный подход «нарезает» окружающий мир, среду на отдельные предметные области. Междисциплинарный подход допускает прямой перенос методов исследования из одной научной дисциплины в другую, что обусловлено сходством исследуемых предметных областей.

Мультидисциплинарный (полидисциплинарный) подход стремится использовать обобщенную картину предмета исследования, по отношению к которой все ее дисциплинарные картины предстают в качестве частей, поэтому переноса методов исследования из одной дисциплины в другую, как правило, не происходит, и все дисциплины продолжают оставаться в рамках собственных методологических принципов. Сопоставление результатов дисциплинарных исследований в рамках мультидисциплинарного (полидисциплинарного) подхода позволяет найти новые, ранее не обнаруживаемые, сходства исследуемых предметных областей, что генерирует новые междисциплинарные исследования. В качестве удачного опыта междисциплинарного исследования отметим работу В.А. Мельникова «Квантовая экономика» [11]. В свое время квантовая физика обеспечила научно обоснованный «выход за границы» классической физики в сторону микромира, что значительно обогатило научные знания и дало обществу ядерную энергию и нанотехнологии.

В методологии более высокого уровня – трансдисциплинарного исследования как способа расширения научного мировозрения – то или иное явление рассматривается вне рамок какой-либо одной научной дисциплины, при этом «выход» направлен в сторону макромира. Каждый фрагмент этого мира, среды, всякая их область, имеющая естественные физические и/или логические границы, изначально рассматривается как «упорядоченная среда», к исследованию которой можно применить одни и те же принципы, подходы и модели.

Термин «трансдисциплинарность» и его первое определение как размещения междисциплинарных отношений внутри глобальной системы, без строгих границ между дисциплинами, было предложено Жаном Пиаже в 1970 году [1]. Сейчас трансдисциплинарный подход получил «прописку» в системе научных методов, применяемых в различных областях знаний. В современной науке существует четыре вида трансдисциплинарности (по Э. Джаджу) [4]:

- трансдисциплинарность-1, основывается на усилиях формальной взаимосвязи пониманий отдельных дисциплин, обеспечивает формирование логических мета-рамок, посредством которых их знания могут быть интегрированы на более высоком уровне абстракции, чем это происходит в междисциплинарности, часто используется при работе различных экспертных систем и экспертных групп;

- трансдисциплинарность-2 имеет более тесную внутреннюю связь с личным опытом исследователя, включая медитацию;

- трансдисциплинарность-3 связана с использованием генеральных метафор, имеющих фундаментальное познавательное значение, во главу угла ставится единоцентризм и конкретность истины;

- трансдисциплинарность-4, ее методология – это способ понимания, познания и описания объекта в составе Единой упорядоченной среды; способ управления состоянием (гармонизация) объекта и естественной среды его обитания, реализуется в 2-х направлениях: получение новых знаний об окружающем мире, поиск решения сложных многофакторных проблем природы и общества. Базовый принцип – конкретность истины – обусловливает единый порядок, трансдисциплинарная система представлена пространственной, информационной и временной единицами этого порядка.

Отрадно, что в отечественной науке существует русская школа трансдисциплинарности, позволяющая сохранить имеющиеся позиции и конкурентоспособность в мировой науке. Первые теоретические работы по философским аспектам трансдисциплинарности появились в России в 2004–2005 годах (Л.П. Киященко). В 2007 г. создана автономная некоммерческая организация «Институт трансдисциплинарных технологий», основной задачей которого является дальнейшее развитие трансдисциплинарности как самостоятельной научной дисциплины, внедрение в практику решения сложных многофакторных проблем методик и технологий трансдисциплинарного подхода. Однако в ходе 20-тилетней работы выяснилось, что большинство разработанных трансдисциплинарных технологий и технологических идей, подготовленных к практической реализации, имеют «двойное назначение», что обусловило избирательность публикаций по отдельным темам в открытой печати. К 2013 г. сформировалось несколько основных отраслевых направлений, где достигнута наибольшая практическая реализация с позиций трандисциплинарного подхода – экономика, экология, образование, здравоохранение, архитектура и строительство, профилактика антиобщественной и террористической опасности.

Авторы полагают, что в современной науке, с учетом мировых трендов ее развития, должно быть уделено подобающее внимание использованию теорий и концепций, имеющих трансдисциплинарный характер в качестве базовых методологических подходов. Одним из трансдисциплинарных подходов, имеющих значительный потенциал в экономических исследованиях, по мнению авторов, является теория игр. Использование математических методов, к числу которых относится теория игр, в анализе экономических процессов позволяет выявить такие тенденции, взаимосвязи, которые остаются скрытыми при применении других методов, и даже получить весьма неожиданные результаты.

Отметим, что теория игр относится к числу наиболее молодых математических дисциплин. Ее возникновение как самостоятельной отрасли математики относят к середине 50-х, когда вышла известная монография Неймана и Моргенштерна «Теория игр и экономического поведения» [13]. Истоки теории игр связаны с работами Э. Бореля (1921 г.). К настоящему времени теория игр превратилась в целое математическое направление, богатое интересными результатами и имеющее большое количество практических рекомендаций и приложений.

Рассмотрим основные понятия теории игр. Каждая формализованная игра характеризуется:

- количеством участвующих субъектов, называемых игроками;

- возможным для каждого из игроков набором действий, называемых стратегиями;

- функциями выигрыша (платежа), отражающими степень удовлетворения интересов каждого из игроков;

- результатом игры, к которому приводят выбранные игроками стратегии и который в свою очередь определяет выигрыш (проигрыш) каждого из игроков.

В дальнейшем теория игр дополнилась новыми интересными разработками. Одна из них – равновесие Нэша. Этот принцип теории игр означает, что каждый игрок делает наилучшее, что он может делать при заданных действиях других игроков или игрока (оппонента), в результате чего ни один из игроков не имеет стимула к изменению своего положения.

Существуют разные способы описания игр. Один из них состоит в том, что рассматриваются все возможные стратегии игроков и определяются платежи, соответствующие любой возможной комбинации стратегий игроков. Игра, описанная таким способом, называется игрой в нормальной форме.

Нормальная форма игры двух участников состоит из двух платежных матриц, показывающих, какую сумму получит каждый из игроков при любой из возможных пар стратегий. Обычно эти матрицы выражают в форме единой матрицы, которую называют биматрицей. Элементами биматрицы являются пары чисел, первое из которых определяет величину выигрыша первого игрока, а второе – величину выигрыша второго. Первый игрок (например, государство) выбирает одну из m стратегий, при этом каждой стратегии соответствует строка матрицы i (i = 1,…, m). Второй игрок (например, бизнес) выбирает одну из n стратегий, при этом каждой стратегии соответствует столбец матрицы j (j = 1,…, n). Пара чисел на пересечении строки и столбца, которые соответствуют стратегиям, выбранным игроками, показывает величину выигрыша каждого из них. В общем случае, если игрок I выбирает стратегию i, а игрок II – стратегию j, то выигрыши первого и второго игроков соответственно равны h¹_ij и h²_ij (i = 1,…, m; j = 1,…, n), где m, n – число конечных стратегий соответственно игрока I и П. Предполагается, что каждому из игроков известны все элементы биматрицы выигрышей. В этом случае их стратегия называется определенной и имеет конечное число вариантов. Если игроку не известны какие-либо варианты стратегий противника (элементы матрицы), то игра называется неопределенной и может иметь бесконечное число вариантов (стратегий).

Существуют и другие классы игр, где игроки выигрывают и проигрывают одновременно.

Антагонистические игры двух лиц связаны с тем, что один из игроков выигрывает ровно столько, сколько проигрывает другой. В таких играх интересы ее игроков прямо противоположны друг другу.

В качестве примера рассмотрим игру, в которой участвуют два игрока, каждый из них имеет по две стратегии. Выигрыши каждого из игроков определяются такими правилами:

- если оба игрока выбирают стратегии с одинаковыми номерами (игрок I – i₁, игрок II – j₁), то первый игрок выигрывает, а второй проигрывает (государство повышает налоги – бизнес платит их, т.е. выигрыш государства определяет проигрыш бизнеса);

- если оба игрока выбирают разные стратегии (игрок I – i₁, игрок II – j₂ , то первый проигрывает, а второй выигрывает (государство повышает налоги на бизнес – бизнес уклоняется от них; проигрыш государства – выигрыш бизнеса).

Биматрица выигрышей игроков будет иметь вид:

Анализ биматрицы показывает, что в антагонистической игре сумма выигрышей игроков I и II равна нулю, т.е.

h^I _ij + h^II _ij = 0, h^I _ij = – h^II _ij. (1)

Теория игр есть теория математических моделей таких явлений, в которых участники («игроки») имеют различные интересы и располагают для достижения своих целей более или менее свободно выбираемыми путями («стратегиями»). В большинстве работ по теории игр предполагается, что интересы участников игры поддаются количественному измерению и являются вещественными функциями ситуаций, т.е. наборов стратегий, получаемых при выборе каждым из игроков некоторой своей стратегии. Для получения результатов необходимо рассматривать те или иные классы игр, выделенные некоторыми ограничительными предположениями. Такие ограничения можно накладывать несколькими путями. Рассмотрим их применительно к взаимоотношениям двух основных игроков экономики – бизнеса и государства. Можно выделить несколько способов (путей) наложения ограничений.

1. Ограничения возможностей взаимоотношений игроков между собой. Простейшим случаем является такой, когда игроки действуют совершенно разобщенно и не могут сознательно помогать или мешать друг другу действием или бездействием, информацией или дезинформацией. Такое положение дел неизбежно наступает, когда в игре участвуют только два игрока (государство и бизнес), имеющие диаметрально противоположные интересы: увеличение выигрыша одного из них означает уменьшение выигрыша другого, и притом на ту же сумму, при условии, что выигрыши обоих игроков выражаются в одинаковых единицах измерения. Не нарушая общности, можно принять суммарный выигрыш обоих игроков равным нулю и трактовать выигрыш одного из них как проигрыш другого.

Эти игры называются антагонистическими (или играми с нулевой суммой, или нулевые игры двух лиц). Они предполагают, что никаких взаимоотношений между игроками, никаких компромиссов, обменов информацией, а в нашем исследовании – и другими ресурсами, не может быть по самой природе вещей, по сути игры, поскольку каждое сообщение, получаемое игроком о намерениях другого, может лишь увеличить выигрыш первого игрока и тем самым увеличить проигрыш его противника.

Таким образом, сделаем вывод, что в антагонистических играх игрокам можно не иметь непосредственных взаимоотношений и вместе с тем находиться в состоянии игры (противостоянии) по отношению друг к другу.

2. Ограничения или упрощающие предположения на множества стратегий игроков. В наиболее простом случае эти множестве стратегий конечны, что устраняет ситуации, связанные с возможными совпадениями (сходимостями) в множествах стратегий, избавляет от необходимости вводить на множествах какую-либо топологию.

Игры, в которых множества стратегий каждого из игроков конечны, называются конечными играми.

3. Предположения о внутреннем строении каждой стратегии, т.е. о ее содержании. Так, например, в качестве стратегий можно рассматривать функции времени (непрерывного или дискретного), значениями которых являются действия игрока в соответствующий момент. Эти и подобные им игры принято называть динамическими (позиционными).

Полагаем, что ограничениями стратегий игроков могут быть и их целевые функции, т.е. определение тех целей, на реализацию которых направлена та или иная стратегия. Можно предположить, что ограничения на стратегию связаны и со способами достижения этих целей в тех или иных временных интервалах, например, стремление бизнеса добиться снижения размеров обязательных налоговых платежей, продаж валютной выручки в краткосрочном периоде. Если же предположений о природе стратегий не делается, они считаются тогда некоторого абстрактного множества. Такого рода игры в самой простой постановке вопроса называются играми в нормальной форме.

Конечные антагонистические игры в нормальной форме называются матричными. Это название объясняется возможностью следующей интерпретациии игр такого типа. Будем понимать стратегии первого игрока (игрок I – государство) как строки некоторой матрицы, а стратегии второго игрока (игрок II – бизнес) – как ее столбцы. Для краткости стратегиями игроков называют не сами строки или столбцы матрицы, а их номера. Тогда ситуациями игры оказываются клетки этой матрицы, стоящие на пересечениях каждой строки с каждым из столбцов. Заполнив эти клетки-ситуации числами, описывающими выигрыши игрока I в этих ситуациях, мы завершим задание игры. Полученная матрица называется матрицей выигрыша игры, или матрицей игры. Ввиду антагонистичности матричной игры выигрыш игрока II в каждой ситуации вполне определяется выигрышем игрока I в этой ситуации, отличаясь от него только знаком. Поэтому дополнительных указаний о функции выигрыша игрока II в матричной игре не требуется.

Матрицу, имеющую m строк и n столбцов, называют (m х n) – матрицей, а игру с этой матрицей – (m х n) – игрой.

Процесс (m х n) – игры с матрицей можно представить следующим образом:

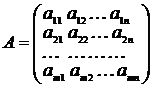. (2)

Игрок I фиксирует номер строки i, а игрок II – номер столбца j, после чего первый игрок получает от своего противника сумму аϊj.

Целью игрока I в матричной игре является получение максимального выигрыша, цель игрока II состоит в том, чтобы дать игроку I минимальный выигрыш.

Пусть игрок I (государство) выбирает некоторую свою стратегию i. Тогда в наихудшем случае он получит выигрыш min аij. В теории игр игроки предполагаются осторожными, рассчитывающими на наименее благоприятный для себя поворот событий.

Такое наименее благоприятное для игрока I положение дел может наступить, например, в том случае, когда стратегия i станет известной игроку II (бизнес). Предвидя такую возможность, игрок I должен выбирать свою стратегию iо так, чтобы максимизировать этот минимальный выигрыш:

.

Значение, стоящее в правой части равенства, является гарантированным выигрышем игрока I. Игрок II (бизнес) должен выбрать такую стратегию jо, что

.

Значение, стоящее в правой части равенства, является выигрышем игрока I, больше которого он при правильных действиях противника получить не может.

Фактический выигрыш игрока I должен при разумных действиях партнеров находиться в интервале между значениями выигрыша в первом и втором случаях. Если эти значения равны, то выигрыш игрока I является вполне определенным числом, сами игры называется вполне определенным, а выигрыш игрока I называется значением игры и он равен элементу матрицы .

У игроков могут быть дополнительные возможности – выбор своих стратегий случайно и независимо друг от друга (стратегии соответствуют строкам и столбцам матрицы). Случайный выбор игроком своих стратегий называется смешанной стратегией этого игрока. В (m x n)-игре смешанные стратегии игрока I определяются наборами вероятностей Х=(х₁,…, х_m), с которыми этот игрок выбирает свои первоначальные, чистые стратегии.

В основе теории матричных игр лежит теорема Неймана об активных стратегиях: «Если один из игроков придерживается своей оптимальной стратегии, то выигрыш остается неизменным и равным цене игры V независимо от того, что делает другой игрок, если он не выходит за пределы своих активных стратегий (т.е. пользуется любой из них в чистом виде или смешивает их в любых пропорциях» [13]. Отметим, что активной называется чистая стратегия игрока, входящая в его оптимальную смешанную стратегию с отличной от нуля вероятностью.

Главная цель игры – нахождение оптимальной стратегии для обоих игроков, если не с максимальным выигрышем одного из них, то тогда с минимальным проигрышем для обоих. Метод нахождения оптимальных стратегий дает часто больше, чем это необходимо для практических целей.

В матричной игре необязательно, чтобы игрок знал все свои оптимальные стратегии, поскольку они все взаимозаменяемы, и игроку для успешной игры достаточно знать одну из них. Поэтому применительно к матричным играм актуальным является вопрос о нахождении хотя бы одной оптимальной стратегии для каждого из игроков.

Основная теорема о матричных играх устанавливает существование значения игры и оптимальных смешанных стратегий для обоих игроков. Оптимальная стратегия не обязана быть единственной. Это очень важный вывод, полученный на основе теории игр.

В нашем исследовании мы будем исходить из предположения, что для играющего в матричную игру субъекта характерны следующие качества:

- элементы матрицы интерпретируются как денежные платежи, и соответственно, их выигрыш и проигрыш оценивается в денежной форме;

- каждый из игроков применяет к этим элементам функцию полезности;

- в игре каждый игрок действует так, как если бы функция полезности его оппонента оказывала на матрицу точно такое же воздействие, т.е. каждый смотрит на игру со своей колокольни.

Эти предположения приводят к играм с ненулевой суммой, в которых возникают отношения кооперирования, торгов и другого типа взаимодействий между игроками как до начала игры, так и в ее процессе.

Обобщение теории игр, имеющее целью включение в нее других возможностей анализа, приводят к интересным, но достаточно трудным задачам. При развитии теории игр необходимо применять функцию полезности не только к денежным исходам, но и как суммам с ожидаемыми будущими исходами. Это предположение является спорным, но мы считаем возможным его допустить. В данном случае мы исходим из того, что это предположение о подобной операции имеет сходство с поведением игроков в определенных ситуациях принятия решений и допускает возможность, что способ ведения игры данным игроком зависит от состояния его капитала во время ведения им игры.

Рассмотрим это на следующем примере. Пусть первый игрок к моменту начала игры g обладает капиталом в x долларов. Тогда его капитал в конце игры будет равен g_ij + x, где g_ij – получаемый им от игры фактический выигрыш. Полезность, которую он приписывает такому исходу, равна f (g_ij + х), где f – функция полезности.

Аналогично, если второй игрок в начале игры имеет капитал в z долларов и его капитал в конце игры с учетом проигрыша (p_ij) составляет z + p_ij, то он оценивает полезность результата по формуле f = (z + p_ij).

Отметим, что у игроков может быть различное субъективное отношение и экономическая оценка достигаемой функции полезности. Одно из них характеризуется тем, что игрок оценивает полезность своего выигрыша в соответствии с его величиной (чем больше выигрыш – тем выше оценка его полезности). Это отношение следует назвать рациональным.

Другой тип отношений связан с сосредоточением игроком своего внимания на выигрыше больших сумм, и для него значительный выигрыш представляется еще большим, чем он есть в действительности, а большие проигрыши он преуменьшает. Это отношение обусловлено наличием у игрока до наступления данной игры больших денежных сумм.

Третий тип отношения игрока к своей игре связан со стремлением избежать больших проигрышей, поэтому он преувеличивает большие проигрыши и соответственно преуменьшает большие выигрыши.

Есть отдельные интересные ситуации. «Выигрывающее отношение» – это отношение игрока, который, помимо фиксирования величины своего выигрыша или проигрыша, назначает еще положительную премию за выигрыши и отрицательную за проигрыши.

«Отчаянное отношение» – это отношение игрока, который должен во что бы то ни стало выиграть данную сумму денег. Любое количество денег, меньше этой суммы, не имеет для него никакой ценности, однако и любое количество денег сверх этой суммы он также не ценит.

Обратим внимание на то, что оценка достигаемой полезности выигрыша производится каждым игроком субъективно и нередко независимо друг от друга. Это означает, что каждый из игроков может по-разному интерпретировать полученный результат, являющийся оптимальным, и в зависимости от этого проявлять большую (или меньшую) активность и заинтересованность в игре. Для оценки полезности результата для каждого игрока имеет значение величина его капитала до вступления в игру и скорость его увеличения (сокращения) во время игры.

Таким образом, наряду с реальной величиной выигрыша (проигрыша) игроков необходимо учитывать различное субъективное отношение игроков к данной игре и их экономическую оценку достигаемой цели и ее полезности, значимости игры в целом.

Отметим, что теория игр применяется к экономическим ситуациям, в которых принятие хозяйственных решений осуществляется в условиях неопределенности, т.е. когда невозможно однозначно определить основные параметры и переменные модели изучаемого процесса или явления. Возможные действия каждой из сторон, называемые стратегиями, также имеют свою классификацию. Стратегии бывают чистыми и смешанными. Чистая стратегия ориентирована на определенное поведение игрока-противника. Смешанная стратегия ориентирована на несколько возможных стратегий поведения игрока- противника.

Существуют различные классификации игр: по числу игроков, по числу стратегий, по свойствам функции выигрыша, по возможности предварительных переговоров и взаимодействия между игроками в ходе игры.

По числу игроков различают игры с двумя, тремя и большим числом игроком. По количеству стратегий различают конечные и бесконечные игры. В конечных играх участники обладают конечным числом стратегий, в бесконечных играх соответственно с бесконечным числом. По свойствам функций выигрыша различают игры с нулевой суммой (антагонистические), т.е. игры, в которых есть прямой конфликт и выигрыш одного участника равен проигрышу второго, и игры с постоянной разностью, т.е. такие, в которых игроки проигрывают и выигрывают одновременно.

В зависимости от возможности предварительных переговоров между игроками различают кооперативные игры (с согласованностью принимаемых решений) и некооперативные игры (без предварительных переговоров и согласованности действий игроков), игры можно различать по объему информации, имеющейся у игроков относительно прошлых ходов. В этой связи они делятся на игры с полной и неполной информацией.

Применение потенциала трансдисциплинарных подходов, в данном варианте – теории игр, в прикладном аспекте исследования взаимоотношений государства и бизнеса позволило получить следующие результаты. Во взаимоотношениях бизнеса и государства, представленных как различные типы игр, всегда можно найти оптимальные стратегии, и их может быть не единичное число, а некоторое множество (область оптимальных стратегий). Это особенно важно для поиска и разработки оптимальных стратегий даже в антагонистических играх, где интересы участников игры противоположны, для формирования партнерских отношений государства и бизнеса. Применение теории игр позволяет спрогнозировать алгоритм действий игроков, поскольку, проиграв в одной игре, игроки начинают или активизируют свои действия в тех видах игр, где их выигрыш наиболее вероятен.

В данном исследовании с позиций трандисциплинарного подхода, а именно, теории игр, взаимоотношения государства и бизнеса представлены как различные виды игр, где главной задачей является нахождение решения игры, т.е. определения оптимальных стратегий (или стратегии), применяемых для достижения соответствующих целей и макроэкономических параметров. Взаимоотношения государства и бизнеса, а также различных бизнес-структур – это своего рода различные виды игр, осуществляемые ими в сфере производства, обращения, в реальном и монетарном секторах экономики, в отраслях и на уровнях хозяйствования, на национальных и мировых рынках. Использование потенциала трансдисциплинарных подходов и, прежде всего, теории игр в анализе общественных и экономических процессов, в данном варианте – к анализу взаимоотношений государства и бизнеса, позволяет выявить их новые качества как игроков и присущие их взаимоотношениям тенденции, что особенно важно в условиях усиления глобализации национальных экономик.

Авторы полагают, что существуют и другие перспективные трансдисциплинарные теории, присущие им методологические подходы, применимые в экономической области исследования:

- теория аутопойезиса (основатели – У. Матурана и Ф. Варела, 1970 г.), согласно которой механизм, превращающий системы в автономные единства, проявляется через аутопойезис – процесс воспроизводства (самопорождения) системой своих компонентов с целью сохранения своей самотождественности. Применение теории аутопойезиса позволяет расширить методологическую базу и предметное поле научного исследования, выявить «зоны самовоссоздания» в инновационной среде и разработать адекватные механизмы институционального управления;

- теория сложности (complexity) обобщает целую совокупность новых междисциплинарных и трансдисциплинарных подходов, фокусируется на процессах генерации и развития самоорганизующихся структур в системах, являющихся динамическими, эмерджентными, фактальными, нелинейными. Теория сложности основана на посылке, когда теория хаоса, нелинейность и сложность рассматриваются как единая парадигма. Теория сложности базируется на базовых понятиях: адаптивность, самотождественность или фрактальность, когда отдельные элементы и подсистемы на различных уровнях единой целостной системы подобны между собой, самоорганизация и саморегуляция, аттракторы – совокупность эндогенных и экзогенных условий, соотношение которых в пространстве и времени меняется хаотично, «грань хаоса», представляющая собой пограничное состояние, узкую зону между системой, которая находится в состоянии равновесия, порядка, и хаосом, который разрушает эту систему. Именно в таком состоянии систем, находящихся на «грани хаоса», генерируются процессы их самоорганизации, «холмистый ландшафт» – неопределенность и нелинейность процессов обусловливает непредсказуемость в среде сосуществования систем, чередование «холмов успеха и эффективности» с «низинами нестабильности и дисбаланса».

Используя подходы теории сложности, можно исследовать процессы, происходящие в сложной системе, которые никогда в точности не повторяются, приходят в равновесие всякий раз к разным точкам фазовой плоскости, проявляют самотождественность, сами сложные адаптивные системы обладают также способностью к самоорганизации, результат функционирования их не может быть задан заранее, даже с некоторой вероятностной оценкой адекватности;

- теория фракталов, понимающая под ними различные структуры, состоящие из частей, которые в определенном смысле подобны целому, это самоподобные структуры, рекурсивные модели, каждая часть которой повторяет в своем развитии развитие всей модели в целом. Применение фракталов позволяет формализовать сложные процессы и объекты, что ценно в области институционального моделирования, описать нестабильные системы и процессы и, самое главное, предсказать тренды будущего развития таких объектов;

- теория турбулентности, представляющая ее как явление самоорганизации, в результате которого происходят регулярные или нерегулярные, хаотические переходы от беспорядка к порядку и обратно, как особо сложную траекторию движения и национальной экономики, и отдельных субъектов (фирмы) в «вихревом потоке» разнообразных перемен, в котором им приходится постоянно выживать и обеспечивать поступательное движение вперед, как крайнюю степень нестабильности глобальной экономической системы, когда вероятность достижения точки ее бифуркации и/или слома чрезвычайно высока, всепроникающим становится риск в различных секторах экономики. Она позволяет выявить, какие разнонаправленные силы и действия содержит экономическая турбулентность, каковы новые правила игры в этих сложных для всех хозяйствующих субъектов условиях;

- теория экономической генетики, изучающая свойства наследственности и изменчивости различных экономических систем, отношений и взаимосвязей, форм хозяйства, возникающих между субъектами и отражающихся в материальных и идеальных носителях этих отношений (продуктах человеческой жизнедеятельности), позволила обосновать, что эволюция фирмы как института экономики имеет генетическую природу и осуществляется через передачу экономических генов – механизма воспроизведения знаниевых активов о сущностных характеристиках фирмы ее саморегуляции, в т.ч. институциональной, применяемых бизнес-моделях, содержании различных видов факторов производства и их взаимодействии, институциональных противоречиях и способов их разрешения, провалах фирмы и методах их устранения, факторах роста и трендах развития фирмы, ее жизненном цикле.

Заключение

1. Применение трансдисциплинарных подходов в современной науке не только возможно, но и необходимо, поскольку продвигает методологическую основу на более высокий уровень и дает новые, оригинальные и значимые в теоретическом и практическом отношении научные результаты.

2. Трансдисциплинарный подход не только обогащает научные знания, но и позволяет разработать новые технологии управления макрообъектами и макропроцессами, в т.ч. управление общим состоянием объектов природы и общества, управление общим состоянием человека и сложного технического объекта, создание способов и технических средств получения и обработки информации и т.д.

Авторы представляют свой посильный вклад в разработку не только теоретических, но и прикладных аспектов применения трансдисциплинарных подходов в современных экономических исследованиях.