Структура и особенности принятия инвестиционных решений в хедж-фонде

Введение

В условиях неопределенности можно говорить о слабой формализуемости и комплексности некоторых явлений, напрямую влияющих на процесс принятия инвестиционных решений внутри хедж-фонда, а также о необходимости понимания взаимосвязей между огромным количеством экзогенных факторов, определяющих инвестиционную политику инвестиционного фонда. Усложнение современной геополитической ситуации усиливает глобальную неопределённость в финансовом аспекте. В связи с этим такими мощными финансовыми институтами, какими являются хедж-фонды, более востребованы инвестиционные стратегии, для разработки и реализации которых необходимо применение достаточно сложных современных вычислительных технологий, к которым относится и когнитивное моделирование. Применение относящегося к нему инструментария для обоснования инвестиционных решений требует в том числе адаптации положений системного анализа, приемов логико-лингвистического моделирования и элементов системы поддержки принятия решений в процессе формирования альтернативных инвестиционных стратегий.

Научный фундамент исследования - труды зарубежных и отечественных ученых в области теории принятия решений, инвестиционного менеджмента, инвестиционных стратегий, теорией стратегического управления, нечетко-логических построений, теорией системного подхода и ситуационного управления, логико-лингвистического моделирования – научные труды У. Шарпа [1, с. 49-58], Ю. Фама и К. Френча [2, с. 441-463], А. Заде [3, с.87-103], В.Н. Волковой [4, с.727-730], Б.Л. Кукора [1, с. 146-195], Д.А. Поспелова [1, с. 47-51].

Целью исследования является обоснование необходимости и возможности использования методов риск-контроля для поддержки принятия инвестиционных ращений в хедж-фонде. Новизна результатов исследования проявляется в авторских рекомендациях по формализации системы поддержки принятия инвестиционных решений хедж-фонда для достижения целей оптимизации инвестиционного портфеля. Методы исследования – это логика, диалектика, теория систем и системный анализ, экономический анализ стратегий хедж-фонда. Гипотеза исследования состоит в обеспечении информационной достаточности об имеющихся или потенциальных инвестициях хедж-фонда для ликвидации угрозы возникновения противоречий для выбора оптимизационных стратегий инвестиционного портфеля.

1. Содержание методов риск-контроля при принятии инвестиционных решений в хедж-фонде

Как известно, ожидаемая доходность так же называется «ex ante доходность» или «ex ante премия за риск» в момент времени t, т.е., «прогнозируемая доходность». Традиционные активы подвержены достаточно просто идентифицируемым рискам, таким как хвостовой риск (tail risk), риск спада деловой активности, инфляционный риск, риск бизнес-циклов, риск рыночной волатильности и корпоративного дефолта [7, с. 269-293]. Отсюда получаем ожидаемую доходность традиционных активов как сумму реальной доходности (yield) и изменения цены (price return):

(1)

Изменение цены актива (PR) отражает изменения, связанные не только с оценкой стоимости актива, но и с некоторыми техническими параметрами, например, постоянство притока/оттока средств ликвидности в актив. Разбив PR на составляющие, получаем следующую скорректированную и расширенную формулу ожидаемой доходности:

(2)

Это достаточно правдивая репрезентация возникновения премии за риск для таких классов активов, как акции, облигации, недвижимость (имеющих четко определяемые или гарантированные доходности, в том числе дивиденды, купоны, ставки аренды, оценки стоимости и финансовые коэффициенты – P/E, P/B, P/Rent income и т.д.), что может быть стандартизировано и обобщено для других видов активов, таких как сырьевые товары и валюты. В частности, для валют известны как фундаментальные способы оценки, основанные на уровнях инфляции, темпах роста ВВП и т.д., так и опирающиеся на динамику ожидаемой доходности – разница в кросс-валютных процентных ставках [8, с. 397-398].

Альтернативные стратегии, такие как сarry, momentum и стоимостное инвестирование формируются как портфели с комбинацией лонг-шорт позиций по традиционным активам. Выбор весов или доли каждого актива в выбранной стратегии или совокупности альтернативных стратегий, а также определение ребалансировки портфеля, позволяет «заработать» премию за риск, устраняя рыночные неэффективности без прямой зависимости от беты показателя оценки риска традиционных активов [9, c. 40-56].

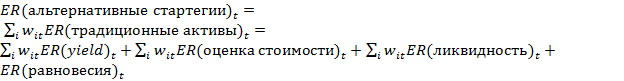(3)

Carry стратегии конструируются из длинных позиций в высокодоходных активах и коротких позиций по низкодоходным активам. Если взять в качестве используемого в стратегии carry актива валюту, то валюты с высокими ключевыми ставками центральных банков будут в длинной позиции у фонда, а валюты с низкой доходностью - в короткой позиции. Разница, возникающая между ставками, и будет являться альфой фонда. Портфолио, построенное на основе данной стратегии, может быть диверсифицировано по огромному количеству валютных пар, что позволит избежать концентрации риска в одной валюте. Классическая финансовая теория отрицает возможность реализации carry стратегий, отталкиваясь от того, что на идеальных рынках возможности арбитража нивелируются за счет паритета процентных ставок, то есть разница в процентных ставках различных валют устраняется изменением обменного курса данных валют, однако, на практике это не подтверждается, высокодоходные валюты доллар и юань на протяжении долгого времени приносят избыточную доходность.

Стратегии, основанные на стоимостном или фундаментальном инвестировании, заключаются в открытии лонг-позиций по активам, которые недооценены рынком по какому-либо стоимостному параметру, и одновременном исполнении шорт-позиций по переоцененным активам. Например, если сравнить акции по значению показателя P/B (Price-to-Book ratio), то акции с низким значением показателя будут покупаться фондом, а с высоким значением – продаваться. Однако, фундаментальные стратегии могут быть рыночно нейтральными, например, когда используются стоимостные показатели (в том числе дивидендная доходность), способные «уравнять» недооцененные и переоцененные компании или активы. На эффективном рынке портфель, состоящий из стоимостных акций или активов, не смог бы опередить по доходности рынок, поскольку премия за риск, заложенная в акции, была бы нивелирована дефолтными активами (то есть теми, которые полностью потеряли бы свою стоимость). Подобная ситуация была продемонстрирована в работе Ю. Фама и К. Френча [10, с. 427-465]. Несмотря на то, что такие характеристики стоимости, как P/B, до сих пор могут быть хорошим инструментом для отбора доходных акций на развивающихся рынках, на развитых же рынках применение данного показателя может привести к потере стоимости портфеля фонда, тогда как отбор активов на основе более сложных показателей или на основе многофакторных моделей может обеспечивать к выдающиеся результаты.

Momentum стратегии отражают набор правил и технических условий, выполнение которых приводит к открытию позиций. Зачастую активы, которые потеряли в стоимости на бычьем рынке, покупаются, а активы, прибавившие в стоимости, продаются. Паттерны для совершения momentum сделок формируются на рынке в случае наличия постоянного притока средств или макротрендов, приводящих к корреляции доходности активов. Momentum так же может быть вызван иррациональным поведением инвесторов, склонных к экстраполяции прошлого поведения цены, что приводит к переизбытку ликвидности в популярных активах и её недостатку в «непопулярных» и падающих в цене активах. Наглядном примером из истории финансовых рынков может послужить пузырь на рынке доткомов в конце 90-х годов прошлого века. Другой причиной существования momentum стратегий являются разрывы циклов спроса и предложения. Объясняется это сложностью и длительностью цикла производства в некоторых отраслях, таких как энергетика, добыча полезных ископаемых и т.д.

Возможность использования подобных комбинаций лонг-шорт позиций позволяет фондам формировать стратегии, минимизирующие подверженность риску, присущему каждому отдельному традиционному активу. Таким образом, ожидаемая доходность фонда может быть выражена следующим уравнением:

(4)

Важно отметить, что при формировании альтернативных стратегий на основе традиционных активов может так же быть получена дополнительная внутренняя доходность от использования производных инструментов на традиционные активы – фьючерсы, опционы, свопы. В связи с этим, хедж-фонды способны реализовывать еще один вид стратегий, который выделяют не по критерию ожидаемой премии за риск (как в случае стратегий momentum, carry и стоимостного инвестирования), а по влиянию на ожидаемую доходность волатильности [11, с. 92-99]. По причине того, что каждый риск-фактор подвержен волатильности, возникают различия между реальной доходностью стратегии («ex-post») и прогнозируемой («ex-ante»).

Например, если при реализации фундаментальной стратегии инвестирования базовый актив окажется дефолтным, стратегия хеджирования может привести к негативной доходности, поскольку систематический риск не был нивелирован и волатильность вносит в планирование и имплементацию бизнес-решений фонда неопределенность. Так же влияют факторы инфляции, дефляции или дефолта отдельных стран на carry стратегии с базовым активом в виде процентных ставок. Однако, данная неопределенность так же может оцениваться и приносить фонду дополнительную прибыль в виде премии за волатильность для каждого риск-фактора.

(5)

Премия за волатильность по своей природе неявно заложена в цену актива, а зачастую в явной форме заложена в оценку деривативных инструментов. У хедж-фондов есть возможность для торговли с помощью опционов внутренней волатильностью базового актива, которая отражает ожидания рынка относительно динамики волатильности. Оценка премии за волатильность (в опционах) может отличаться в зависимости от базового актива. Различные уровни премии за волатильность объясняются отсутствием гомогенности рыночного риска, а также различным восприятием риска участниками рынка. Это приводит к временным (или среднесрочным) колебаниям премии за защиту от волатильности, то есть колебаниям спроса и предложения на подверженность волатильности.

Например, Volatility Risk Premium (VRP) [12, с. 2471-2511] исторически для индекса S&P500 был в 90% случаев выше 0, то есть положительным, что говорит о высоком спросе инвесторов и фондов на защиту от волатильности, в то время как тот же показатель для валют торгуется на более низких ценах. Объясняется это в том числе тем, что акции используются преимущественно в длинных торговых стратегиях «buy-and-hold», а валюты открываются в 50% случаев в длинных, а в 50% случаев в коротких позициях. Учитывая такое различие в премии за волатильность, фонды способны конструировать систематические стратегии, основанные на продаже дорогих VRP и покупке дешевых, поэтому волатильность как риск-фактор также входит в классификацию используемых и учитываемых хедж-фондами рисков при планировании и реализации их инвестиционных решений.

Таким образом, классификацию риск-факторов или альтернативных стратегий на базе учитываемых рисков можно представить в виде традиционных стратегий, carry, momentum, фундаментальной оценки и волатильности (рис.1).

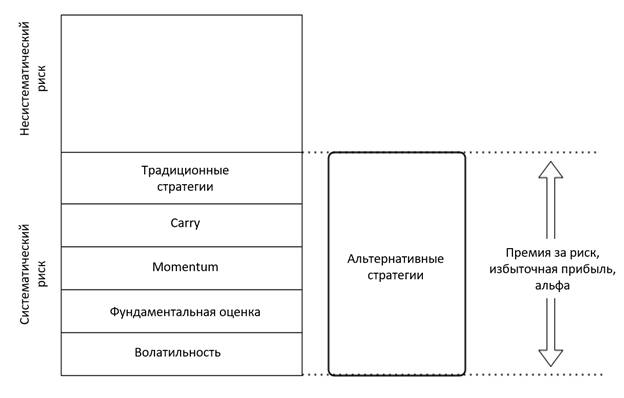
Рис.1. Взаимосвязь систематического риска, альтернативных стратегий и риск-факторов

Источник: составлено авторами

2. Распределение риска как функция контроля

Рассмотрев основные шаги принятия инвестиционных решений на этапах зарождения идеи, ее формализации и выбора типа применяемой стратегии, авторы считают важным обратить внимание на теоретические аспекты последнего этапа инвестиционного планирования в хедж-фондах, а именно – на контроль рисков через оптимизацию портфеля активов, что необходимо для достижения максимально эффективного распределения весов активов в портфеле с точки зрения совокупной доходности стратегии. Это стоит сделать прежде, чем обращаться к моделированию системы поддержки принятия решений. Оптимизация портфеля может быть задана исходя как из внутренних ограничений (ликвидность рынка отдельного актива, несистематические риски, цена и т.д.), так и из внешних, учитывая в том числе требование инвесторами небольшого риска, высокого коэффициента Шарпа, кратковременности инвестиций и т.п. [13, с. 12-38]

Процесс оптимизации сугубо математическая процедура, она описывается через статистическо-математические методы, что существенно упрощает задачу достижения максимальной эффективности при принятии инвестиционных решений. Однако для получения надежного результата при выборе весов активов нужны точные прогнозы ожидаемой доходности по каждому отдельному активу, ожидаемой волатильности и корреляции между ними. Это делает практически невозможным исключение статистических погрешностей и предвзятости при формировании инвестиционного портфеля. Для целей данной статьи приведём упрощенный вариант математического описания определения весов оптимизации посредством функции полезности инвестора. Задачу управляющего фонда по повышению доходности инвесторов можно выразить через функцию полезности, которая выглядит следующим образом:

(6)

Для повышения полезности функции управляющему фонда приходится распределять доли активов таким образом, чтобы ожидаемая доходность была максимальной, а взвешенная по риску волатильность была на наименьшем уровне. Функция неприятия риска (вес по риску) как раз и описывает характер поведения альтернативных издержек в диапазоне между ожидаемым риском и доходностью. Г. Леви и Г. М. Марковиц доказали, что функция полезности в таком простом виде способна давать оптимальные решения для большого круга функций полезности, то есть для широкого круга инвесторов [14, c. 308-317]. Инвестиционный портфель, построенный с учетом данной функции, так же будет давать максимально возможный коэффициент Шарпа как показателя эффективности деятельности менеджера фонда.

3. Методы оптимизации портфеля активов

Рассмотрим основные методы оптимизации портфеля активов (табл.2).

Табл. 2 Методы портфельной оптимизации, их задачи и условия достижения оптимальности

Более детально разберем некоторые из методов оптимизации.

Mean-Variance Optimization (MVO). Оптимизация по средней дисперсии ставит задачу формирования такого портфеля, для которого коэффициент Шарпа будет иметь наибольшую величину. Достигается это за счет максимизации функции полезности инвестора (в данном случае хедж-фонда).

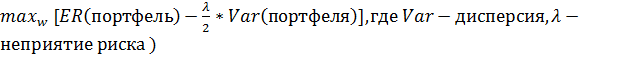(7)

Чем больше , тем больший вес фонд придает менее рискованным активам и меньший вес более рискованным. Если , то используя MVO, инвестиционный управляющий должен будет распределить 100% денежных или ликвидных средств в один, максимально доходный актив. Если же , то фонд отдает предпочтение минимизации риска, а не достижению максимальной доходности, что трансформирует MVO в другой метод оптимизации - GMV (global minimum variance).

Global Minimum Variance (GMV). Имея в виду потенциальные недостатки MVO, связанные с чувствительностью прогнозов доходности актива (входные данные), большинство фондов и инвестиционных менеджеров отдают предпочтение портфелям, взвешенные исключительно по риску. Стремление к применению взвешенных по риску моделей всегда оказывается простимулирован финансовым кризисом, поскольку и институциональные, и частные инвесторы становятся более восприимчивы к риску больших потерь.

GMV представляет собой частный случай MVO, когда хедж-фонд имеет задачу полностью исключить риски. В данном случае «избегание риска» преобладает над «максимизацией доходности» и задача оптимизации сводится к определению таких весов активов, которые приведут к минимально возможной волатильности портфеля. Расчет осуществляют, основываясь на ковариационной матрице доходности:

(7)

Most-Diversified Portfolio (MDP). Другой популярный метод оптимизации базируется исключительно на прогнозном риске, то есть волатильности, и не требует прогнозирования доходности, это метод MDP. Данный метод максимизирует коэффициент диверсификации портфеля, который определяется как взвешенная средняя волатильность по всем активам к общей волатильности портфеля. Другими словами, данный метод позволяет нивелировать эффект коррелированности между инвестициями и снизить волатильность всего портфеля. Простейшим примером такой диверсификации будет портфель, состоящий только из облигаций и акций. Если акции резко вырастут в цене, а облигации упадут, то, в общем и целом, каждая позиция хедж-фонда будет подвержена колоссальной волатильности, однако доходы от роста стоимости акций могут превысить потери по облигациям, что, в свою очередь, обеспечит константу стоимости позиции (стоимость не изменится), что будет свидетельствовать о низкой общей волатильности портфеля.

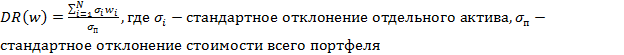(8)

Для коррелированных активов MDP дает управляющему фонда простое представление о распределении долей между инвестициями обратно пропорционально их индивидуальной волатильности. В частном случае, когда активы не коррелированы, данный метод трансформируется в метод равной маржинальной волатильности (EVM).

Risk Budgeting (RB). Если приведенные выше теоретические положения выведены статистическими методами и на основе математически обоснованной функции полезности инвестора, то бюджетирование риска представляет собой альтернативный подход к оптимизации весовых коэффициентов при формировании инвестиционного портфеля. Для начала портфельному управляющему фонда необходимо распределить максимальные значения вносимого каждым отдельным активом риска. Чаще всего это делается на основе личного опыта или текущего видения рынка. Например, сырьевые товары должны вносить 10% от общего риска портфеля, акции - 50% и так далее. Такие риск-уровни в совокупности по всем активам будут составлять 100% от общего риска портфеля. Важно отметить, что при RB весовые коэффициенты активов будут равны риск-уровням, деленным на соответствующие беты активов. Таким образом, сам по себе метод так же во многом зависит от качества прогноза беты или ожидаемой беты активов по отношению ко всему портфелю фонда.

Black-Litterman (BL). Фреймворк для оптимизации инвестиционного портфеля был представлен Ф. Блэком и Р. Литтерманом [15, с. 23-26] для решения проблемы использования MVO в условиях неопределенности и ненадежности прогнозов будущей доходности активов. В модели BL используются статистические методы, чтобы инкорпорировать информацию о рыночной конъюнктуре и представлениях менеджера фонда в расчет весов для каждого отдельного актива. Такая процедура оценки должна приводить к более робастным (стабильным) MVO весам.

Метод можно разложить на две составляющие:

1. Априорная - поиск «внутренней» доходности каждого актива с помощью поиска ожидаемой доходности через моделирование MVO на основе рыночных весов активов.

2. Апостериорная – включение в модель будущих ожиданий инвестора относительно доходности активов.

Комбинация этих двух составляющих осуществляется посредством байесовской оптимизации (условной вероятности) для определения будущего распределения доходности. Взяв , где α-средняя ожидаемая рыночная доходность, θ∑ -стандартное отклонение доходности, умноженное на несоответствие ожиданий инвестора и рынка, в качестве априорной доходности и ожидания менеджера фонда как , где Pr - средняя ожидаемая условная доходность, M - стандартное отклонение доходности, можно получить вектор который так же будет иметь нормальное распределение. Далее для расчета весов необходимо использовать ту же функцию полезности инвестора, что и в случае MVO, с заменой ожидаемой доходности на условную, а неприятия к риску - на вектор .

Таким образом, рассмотрев основные аспекты управления процессом принятия решений в хедж-фондах, авторы считают, что фундаментально можно выделить следующие особенности, формализующие данный процесс:

1) Организационная структура с разделением функции предоставления ликвидности и управления (агентская проблема, инвестор - управляющий фонда).

2) Сложный процесс формирования стратегий фонда из-за необходимости хеджирования позиций и получения чистой альфы от инвестиций.

3) Контроль рисков через оптимизацию портфеля, учитывающий неоднозначность выбора методов оптимизации.

Наряду с этим, хедж-фонд должен планировать стратегическое развитие, быть на передовой линии научно-технического прогресса из-за постоянной конкуренции и необходимости ускорения принятия инвестиционных решений, в том числе по причине широкого распространения фондов высокочастотной торговли HFT (high-frequency trading), способных использовать стратегии, недоступные «отставшему» в технологиях хедж-фонду.

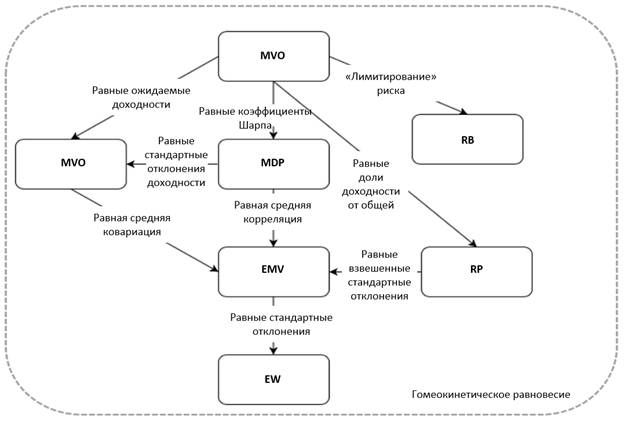
Рис. 2 Взаимосвязи между различными стратегиями оптимизации портфеля

Источник: составлено авторами

Все эти риски требуют создания гибкого и высокоэффективного инструментария по принятию инвестиционных решений, который бы реплицировал действия и мыслительный процесс управляющего фонда, исключая влияние случайных факторов и ошибок, таким инструментарием может служить система поддержки принятия решений [16, с. 223-238].

Для целей формализации системы поддержки принятия решений (СППР) будет сравнение предложенных альтернативных сценариев и выбор наиболее оптимального (в зависимости от введенных ограничений или критериев) [17, c. 2933-2946]. Это можно продемонстрировать на основе исторических показателей доходности стратегий фонда Bridgewater LLC как крупнейшего в мире хедж-фонда, рассмотрев его портфель, риски и доходности по трем классам активов, в которых позиции хедж-фонда являются основными: акции компаний (emerging markets), корпоративные облигации и деривативные инструменты, представленные процентными свопами.

4. Выводы: альтернативные сценарии оптимизации портфеля

Далее найдем и применим альтернативные сценарии оптимизации портфеля, состоящего из трех основных активов. В табл. 3 приведена оценка сценариев портфельной оптимизации для данного хедж-фонда. С целью реализации главной задачи фонда - максимизировать альфу (или повысить альтернативную стоимость портфеля), то есть увеличить избыточную прибыль организации, введем некоторые «ограничители» или критерии эффективности. Это будут: показатель доходность/риск, коэффициент Шарпа, коэффициент диверсификации портфеля. Для показателя доходность риск оптимальным будет показатель больше либо равный 1, такая же ситуация с коэффициентом Шарпа. Для коэффициента диверсификации низшего порога нет, однако, показатели, значительно превышающие 1 являются целевыми. Из проведенного анализа видно, что стратегии полной диверсификации портфеля (MDP) и среднего стандартного отклонения (MVO) являются превалирующими. Несмотря на это, прежде чем определять наиболее предпочтительный метод, требуется решить главную проблемную ситуацию – увеличение доходности и снижения общего риска.

Табл. 3 Оценка сценариев портфельной оптимизации для Bridgewater LLC

Для разрешения последнего класса проблемных ситуаций, введем в анализ дополнительные показатели и рассмотрим портфельные оптимизационные стратегии с точки зрения прогнозной доходности и стандартного отклонения. Исходя из полученных результатов, можно интуитивно предположить, что управляющему необходимо выбрать стратегию EW, поскольку она обеспечивает максимальный возврат на инвестиции. Однако, данная стратегия имеет и максимальный показатель стандартного отклонения доходности, что может привести к полной потере стоимости от полученной доходности активов. Таким образом, анализ более рационально будет проводить с точки зрения разницы между прогнозной доходностью и стандартным отклонением. В результате менеджер хедж-фонд остановит свой выбор на стратегии EMV (equal marginal volatility), где показатель составит +0,3%

Табл. 4 Оценка ожидаемой доходности и волатильности стратегий оптимизации по портфелю, состоящему из трех классов активов для Bridgewater LLC

Для визуальной иллюстрации приведенного сценарного отбора, построим график границы эффективности портфельной оптимизации Г. Марковица [18, с. 77–91]. На графике представим каждый из полученных сценариев портфельной оптимизации (рис. 3). Горизонтальная ось графика отражает волатильность портфеля в то время, как вертикальная ось отражает ожидаемую доходность портфеля. Каждая точка границы эффективности получена путем минимизации волатильности портфеля и максимизации ожидаемой доходности.

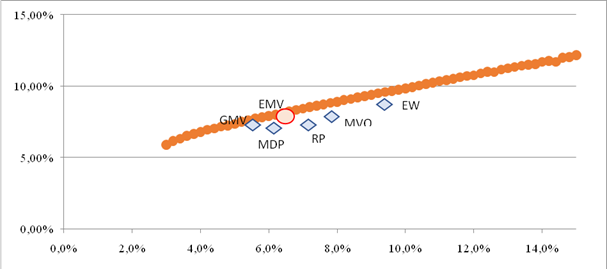
Рис. 3 Граница эффективности и сценарии распределения весов для портфеля Bridgewater LLC из трех классов активов: акции, облигации и процентные свопы

Источник: составлено авторами на основе финансовой отчетности Bridgewater LLC

Рассмотрим полученные результаты для каждой отдельной стратегии.

Equal Weight. Портфель при данной оптимизации остается не полностью диверсифицированным из-за равных весов у каждого актива в портфеле. Если для активов, входящих в портфель, мы имели равные ожидаемые доходности, риска и корреляции, то мы получили бы MVO стратегию.

Equal Marginal Volatility. Как было определено в результате анализа, данная стратегия является оптимальной с позиции показателя «доходность – стандартное отклонение». Несмотря на то, что метод предполагает одинаковый вклад каждого актива в общий риск портфеля, показатели стандартного отклонения для акций, облигаций и процентных свопов отличаются из-за наличия корреляции между ними.

Mean-variance optimization. Данная стратегия обладает максимальным показателем коэффициента Шарпа, однако, в практике MVO не способна принести избыточную прибыль фонду из-за заложенной в модели прогнозной доходности активов, которая зачастую не соответствует реальной.

Global Minimum Variance. Оптимизация по глобальному минимуму волатильности находится в левой части границы эффективности, поскольку она направлена на достижение минимально возможной волатильности портфеля.

Заключение по результатам исследования

Итак, необходимо отметить особую характеристику деятельности хедж-фонда, важную для СППР и связанную с множеством альтернативных сценариев принятия решения управляющим фонда о релокации средств между активами в портфеле. Однако, все известные методы оптимизации портфеля взаимосвязаны между собой через «добавление» или «исключение» предположений о характере законов распределения доходности по классам активов, о неопределенности будущей волатильности активов, об ожиданиях по изменению безрисковой доходности. Взаимная коррелированность стратегий приводит к потенциальной угрозе нарушения эффективности ресурсообеспеченности лица, принимающего решение, при оценке СППР с точки зрения предложенного целевого значения, то есть предложенного разрешения проблемной ситуации.

Решение этой проблемы возможно только через постоянный мониторинг и обновления накопленной базы знаний субъектом управления (менеджером) об объекте управления (инвестиционной стратегии), а также при наличии контроля функционирования потоков между ЭО на основе соответствия потребностей и возможностей посредством логико-лингвистического моделирования (фреймов) в целях сохранения гомеокинетического равновесия системы, поскольку выбранная стратегия инвестирования не должна нарушать данное равновесие [19, с. 98-101]. Таким образом, обеспечение информационной достаточности об имеющихся или потенциальных инвестициях фонда приведет к тому, что не будет угрозы возникновения противоречий по поводу того, какую оптимизационную стратегию выбрать.

Итак, в статье была рассмотрена проблема и ограничения особенностей принятия инвестиционных решений хедж-фонда, для решений данной проблемы бы систематизирован и описан спектр возможных альтернативных стратегий, используемых при формировании инвестиционных решений в хедж-фондах с учетом основных методов СППР. Основное внимание уделено риск-факторам, которые определяют подверженность инвестиционной стратегии (или инвестиционной идеи) фонда систематическим рискам, и способам нивелирования этого риска. Кроме того, была апробирована СППР для Bridgewater LLC с целью принятия решения по выбору стратегии инвестирования и оптимизации портфеля фонда на основе оценки эффективности каждого сценария, возможные направления дальнейших исследований – применение динамического риск-контроля в СППР.