Выбор варианта развития предприятия методами машинного обучения

Введение

Выбор варианта развития для любого предприятия представляет собой важную задачу, от решения которой зависит дальнейшая деятельность. По существу, вариант развития представляет собой стратегию, под которой понимается долгосрочное направление развития организации с целью завоевания наиболее благоприятного положения предприятия среди конкурентов. Иными словами, путь развития – есть набор правил для принятия решений, которыми организация руководствуется в своей деятельности [1, 2] (Ansoff, 2007; Agafonov, 2018). При выборе варианта развития необходимо обосновать перечень показателей, по которым оценивается конкретная стратегия, выявить наиболее пригодный метод для решения этой задачи, проверить работоспособность предложенной методики.

Кратко рассмотрим публикации по исследуемой теме за последние годы, в основном по базе данных ScienceDirect. Первые три промышленные революции произошли в результате механизации, электрофикации и информатизации. Германия предложила концепцию «умного производства» для реализации четвертой промышленной революции, то есть Индустрии 4.0 [3] (Brocal, Sebastián, González, 2019). И на сегодня «цифровизация» стала модным словом, доминирующим в дебатах в советах директоров и стимулирующим беспрецедентные инвестиции. Только в 2019 году было вложено более 1 триллиона долларов в финансирование будущего использования цифровых технологий, будь то корпоративные системы, многоканальные системы, машинное обучение, большие данные и системы поддержки принятия решений, блокчейн или приложения виртуальной и дополненной реальности. В широком смысле цифровизация означает внедрение цифровых технологий для использования во многих сферах социальной жизни, таких как правительство, школьное образование, социальные услуги, здравоохранение, бизнес, оборона, развлечения и игры [4] (Climent, Haftor, 2021).

Аналитика больших данных, т.е. инструменты и процессы, применяемые к большим и сложным наборам данных для получения информации, уже почти десятилетие является центральной темой для обсуждения исследователями и практиками. В большинстве эмпирических исследований на сегодняшний день изучались необходимые инвестиции фирм или дополнительные ресурсы и процессы, которые следует разработать для получения ценности для бизнеса от таких инвестиций. Хотя выделение основных ресурсов при развертывании аналитики больших данных является важным первым шагом, оно не дает ответа на вопрос о том, как аналитика развертывается и связана со стратегией, и особенно какие аспекты этого процесса могут потенциально препятствовать созданию ценности [5] (Mikalef, Wetering, Krogstie, 2021). Количество доступных технологий постоянно растет. Выбор правильных технологий может решить судьбу компании. Из-за огромного количества источников информации регулярные исследования рынка технологий становятся все более сложными.

Неуклонный прогресс в отношении быстрорастущих вычислительных возможностей и распространение свободно доступных программных пакетов повышают удобство использования и расширяют возможности машинного обучения. Помимо таких областей применения, как автономное вождение, биоинформатика, чат-боты или сервисная робототехника, приложения, основанные на машинном обучении, также получают все большее распространение в обрабатывающей промышленности для профилактического обслуживания, управления качеством или управления технологическим процессом [6] (Kißkalt, Mayr, Lutz, Rögele, Franke, 2020).

В последние годы разведочный анализ данных и их аналитика доказали свою ценность для многих организаций. Существующие платформы интеллектуального анализа данных, например межотраслевой стандартный процесс интеллектуального анализа данных (Cross-Industry Standard Process for Data Mining – CRISP-DM), предлагают структурированную и итеративную последовательность действий: формулировка проблемы, анализ данных и аналитическое моделирование. Большинство фреймворков воспринимается как функциональная цепочка от генерации данных до принятия решений. Они показывают, как генерируются, обрабатываются и подготавливаются данные для тех, кто должен принимать решения как на политическом, так и на оперативном уровне [7] (Voort, Bulderen, Cunningham, Janssen, 2021).

Бизнес-аналитика в целом использует операционные исследования, машинное обучение и другие информационные технологии. В этом смысле бизнес-аналитика имеет дело не только с описательными моделями, но и с моделями, способными обеспечить осмысленное понимание и поддержку принятия решений. Бизнес-аналитика развилась за пределы простого анализа необработанных данных на больших наборах данных с целью обеспечения организациям конкурентного преимущества [8] (Lepenioti, Bousdekis, Mentzas, 2020).

Как видно из приведенных выше источников [3–8] (Brocal, Sebastián, González, 2019; Climent, Haftor, 2021; Mikalef, Wetering, Krogstie, 2021; Kißkalt, Mayr, Lutz, Rögele, Franke, 2020; Voort, Bulderen, Cunningham, Janssen, 2021; Lepenioti, Bousdekis, Mentzas, 2020), подавляющая часть организаций понимают возрастающую роль новых технологий, связанных с проникновением искусственного интеллекта во все области науки и технологий. В то же время в проанализированных работах отмечается лишь общее направление исследований, не конкретизирующее применение тех или иных приемов машинного обучения, хотя в поисковую строку ресурса ScienceDirect была введена фраза, совпадающая с названием статьи. Авторы рассматривали подобную задачу с использованием гибридной нейронечеткой системы, представляющей собой объединение нейронных сетей и нечеткой логики [9] (Krichevsky, Martynova, 2019). Здесь же целью работы является выбор варианта развития предприятий не одним заранее определенным методом, а применением для поставленной задачи набора различных способов, из которых затем отбирается наиболее пригодный метод по критерию точности классификации.

Далее статья структурирована следующим образом: вначале описываются и анализируются некоторые методы машинного обучения, пригодные, с точки зрения авторов, для решения поставленной задачи. Затем приводятся полученные результаты и демонстрируется возможность модели в виде метода опорных векторов для выбора варианта развития предприятия.

Методология

1. Машинное обучение

Под термином «машинное обучение» понимается технология, которая в [10] (Alpaydin, 2014) определена следующим образом: «Оптимизация критерия производительности модели с использованием данных и прошлого опыта». У нас есть модель, определенная с точностью до некоторых параметров, а обучение – это выполнение компьютерной программы для оптимизации параметров модели. Указанный термин относится к автоматическому обнаружению значимых закономерностей в данных. За последние 20 лет машинное обучение стало обычным инструментом в любой задаче, требующей извлечения информации из наборов данных. Мы находимся в окружении технологий, основанных на машинном обучении: программы для защиты от спама учатся фильтровать сообщения электронной почты, транзакции по кредитным картам защищены программным обеспечением, которое учится обнаруживать мошенничество, автомобили оборудованы системами предотвращения аварий, созданными с использованием таких алгоритмов [11–13] (Mitchell, 1997; Flakh, 2015; Brink, Richards, Feverolf, 2017).

Область машинного обучения связана с вопросом о том, как построить компьютерные программы, которые автоматически улучшаются с опытом. В последние годы было разработано множество успешных приложений машинного обучения. В то же время были достигнуты важные результаты в теории и алгоритмах, составляющих основу этой сферы знаний. В машинном обучении данные играют незаменимую роль, а алгоритм обучения используется для обнаружения и изучения знаний или свойств из данных. Качество или количество набора данных влияют на эффективность обучения и прогнозирования. Но машинное обучение является частью искусственного интеллекта. Для того чтобы быть интеллектуальной, система, которая находится в изменяющейся окружающей среде, должна иметь возможность обучаться. В этом случае система сама адаптируется к изменениям внешней среды, и разработчик системы не должен предвидеть все возможные ситуации.

Машинное обучение опирается на концепции и результаты из многих областей, включая статистику, искусственный интеллект, философию, теорию информации, биологию, компьютерные науки и теорию управления. Машинное обучение учит компьютеры делать то, что естественно для людей: учиться на практике. Алгоритмы машинного обучения используют вычислительные методы для извлечения информации непосредственно из данных, не полагаясь на предопределенное уравнение в качестве модели. Алгоритмы адаптивно улучшают свою производительность по мере увеличения количества выборок, доступных для обучения.

Опишем методы машинного обучения, отобранные для решения поставленной задачи.

2. Методы классификации вариантов

Для классификации вариантов развития воспользуемся методами деревьев решений, опорных векторов, k-ближайших соседей и дискриминантным анализом. Такой набор инструментов основан, в большей мере на опыте работы авторов статьи с методами машинного обучения, входящими в состав программы MatLab.

2.1. Деревья решений

Дерево решений – это метод аппроксимации целевых функций с дискретными значениями признаков [14] (Azad, Moshkov, 2017). Обычно деревья используются для предсказания размещения классов или объектов в категории по результатам измеряемых параметров. Деревья решений являются одним из наиболее популярных подходов к решению задач добычи данных. Они создают иерархическую структуру классифицирующих правил типа «ЕСЛИ…,ТО…», имеющую вид дерева. Такой метод представляет решающие правила в определенной иерархии, включающей в себя элементы двух типов – узлов и листьев.

Для принятия решения об отнесении некоторого объекта к определенному классу требуется ответить на вопросы, стоящие в узлах этого дерева, начиная с его корня. Вопросы имеют вид «значение параметра А больше В?». Если ответ положительный, осуществляется переход к правому узлу следующего уровня. Затем снова следует вопрос, связанный с соответствующим узлом, и т. д. Приведенный пример иллюстрирует работу так называемых бинарных деревьев решений, в каждом узле которых ветвление производится по двум направлениям (т. е. на вопрос, заданный в узле, имеется только два варианта ответов, например Да или Нет).

Узлы содержат решающие правила и производят проверку примеров на соответствие выбранного атрибута (признака) обучающего множества. Для получения ответа необходимо следовать решениям в дереве от корневого (начального) узла до конечного узла, который содержит ответ. В самой простой ситуации примеры попадают в узел, проходят проверку и разбиваются на два подмножества:

· первое – те, которые удовлетворяют установленному правилу;

· второе – те, которые не удовлетворяют этому правилу.

Далее к каждому подмножеству снова применяется правило, процедура повторяется. Это продолжается до тех пор, пока не будет достигнуто условие остановки алгоритма. Последний узел, когда не осуществляется проверка и разбиение, становится листом. Он определяет решение для каждого попавшего в него примера. Для дерева классификации – это класс, ассоциируемый с узлом.

Эти методы обучения успешно применяются к широкому кругу задач от диагностики медицинских случаев до оценки кредитного риска среди соискателей кредита.

2.2. Метод опорных векторов

Метод опорных векторов (МОВ) – мощный инструмент, используемый для решения проблемы классификации и регрессии. Этот метод выполняет классификацию путем построения N-мерной гиперплоскости, которая оптимально разделяет данные на две категории [15] (Vapnik, 1998). Принципиально всегда возможно преобразовать любое множество данных таким образом, чтобы классы могли быть линейно разделены. Перспективный метод для построения разделяющих функций в задаче классификации или оценки функций в регрессионном анализе связан с теорией МОВ. Этот метод основан на статистической теории обучения, которая играет ключевую роль во многих областях техники, медицины, экономики, в частности:

· прогнозирование стоимости акций на определенный период вперед с использованием данных о финансовом состоянии компании;

· идентификация рукописных цифр в почтовом индексе;

· предсказание состояния больного на основе анализа его электрокардиограммы, давления и других клинических параметров.

Модели этого метода близки к нейронным сетям. На самом деле, модель МОВ с использованием сигмоидной функции ядра эквивалентна персептрону, состоящему из двух слоев нейронов. МОВ предназначен для решения задач классификации путем поиска хороших решающих границ, разделяющих два набора точек, которые принадлежат разным категориям. Для классификации новых точек достаточно проверить, по какую сторону от границы они находятся.

В самом простейшем случае классификации МОВ использует линейную разделяющую гиперплоскость для создания классификатора с максимальным отступом (classifier with a maximal margin). В этом случае проблема обучения сводится к нелинейной задаче оптимизации с ограничениями.

2.3. Метод k-ближайших соседей

Классификация методом ближайшего соседа (k – Nearest Neighbor или k-NN) представляет собой алгоритм машинного обучения, который локализует группу из k объектов в обучающей выборке, находящуюся ближе всего к тестовому объекту.

Модель для k-NN – это весь набор обучающих данных. В процессе обучения алгоритм начинает классификацию только в той ситуации, когда появляются новые неразмеченные данные. Для этого алгоритма необходимы три важных компонента:

· группа размеченных объектов;

· метрика близости;

· число k ближайших соседей.

Популярной метрикой близости, которая используется в этом методе, является евклидово расстояние. При появлении новых данных работа алгоритма k-NN представляет собой последовательность следующих шагов:

1. Определяются k ближайших соседей.

2. С использованием классов соседей алгоритм решает, как лучше классифицировать новые данные.

При сформированном списке k ближайших соседей новые объекты классифицируются в соответствии с принципом большинства. Иными словами, при реализации этого принципа за правильное решение принимается простое большинство. Новую точку данных включают в тот класс, к которому относится наибольшее количество соседей.

2.4. Дискриминантный анализ

В машинном обучении дискриминантный анализ (ДА) применяется для нахождения линейной комбинации признаков, которая характеризует или разделяет два или более классов объектов или событий. Несмотря на долгую историю развития таких методов, модели ДА продолжают активно использоваться и сегодня в различных сферах деятельности [16] (Ezghazi, Zahi, Zekoua, 2017).

Результирующее уравнение может быть использовано в качестве линейного классификатора. ДА стремится максимизировать разделение между классами данных и формирует ровно столько же линейных функций, сколько классов имеется в данных. Предсказанный класс для очередного наблюдения будет тот, который имеет самое высокое значение для линейной функции.

Предполагается, что различные классы генерируют данные на основе разных распределений Гаусса. ДА находит набор прогнозных уравнений, основанных на независимых переменных, которые используются для классификации объектов в группы. Выполнение ДА преследует две цели:

· найти уравнение для классификации новых объектов;

· интерпретировать уравнение для лучшего понимания отношений, существующих среди переменных.

Линейный дискриминант используется часто, главным образом из-за его простоты. Линейная модель легко интерпретируется: выход является взвешенной суммой входных признаков. Большинство функций являются аддитивными, поэтому выход представляет собой сумму эффектов нескольких входов, где веса могут быть положительными (усиливающими) или отрицательными (замедляющими). При анализе всегда вначале используют линейный дискриминант перед тем, как перейти к более сложным моделям.

Результаты

В качестве предприятия, для которого производится выбор варианта развития, воспользуемся данными по реально существующей организации (назовем ее АВС). Эта компания является логистом крупной торговой сети и занимается транспортировкой продукции от производителя в торговые точки сети. В качестве вероятных моделей развития фирмы АВС выберем следующие стратегии: расширение рынка сбыта путем основания дочерней компании (вариант 1); сокращение предприятия (вариант 2) и выживание (вариант 3). Разработанные критерии для оценки трех вариантов развития приведены в таблице 1.

Таблица 1

Критерии оценки

Для создания базы примеров, которые используются для выбора модели классификации, возможно использование двух подходов:

· применение реальных данных;

· использование «игрушечных» наборов данных (toy dataset).

В машинном обучении важно научиться правильно применять игрушечные наборы данных, так как обучение алгоритма на реальных сопряжено с трудностями и может закончиться неудачей [14] (Azad, Moshkov, 2017). Разыгранные наборы данных играют решающую роль для понимания работы алгоритмов. При наличии простой синтетической выборки данных достаточно просто оценить, обучился алгоритм нужному правилу или нет. На реальных данных получить такую оценку сложно. Здесь воспользуемся методом Монте-Карло для формирования игрушечной выборки данных. Созданная таким образом база данных, состоящая из 60 строк (по 20 строк для каждого варианта) и 7 столбцов (6 критериев и индикатор варианта), была введена в программу MatLab. Результаты использования различных классификаторов показаны на рисунке 1.

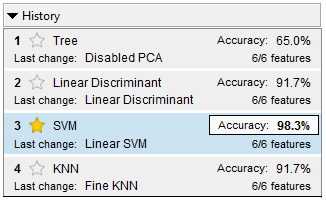
Рисунок 1. Результаты классификации

Источник: получено авторами.

Как видно из рисунка 1, самую высокую точность классификации по обучающей выборке показал метод опорных векторов, который можно использовать для дальнейшей работы. Для проверки работы выбранного классификатора введем значения одного из разыгранных наблюдений первого класса Х1 = [6.57 7.73 6.55 8.08 8.92 9.99], которое программа уже «видела» при обучении. Результат выполнения программы представлен ниже:

>> yfit = trainedModel.predictFcn (x1)

yfit =

1

Как видно, метод опорных векторов правильно классифицировал данное наблюдение. В последующем в зависимости от ситуации, которая складывается в организации, можно применить разработанную модель для выбора стратегии развития компании.

Обсуждение

Приведенные результаты по выбору метода решений, которые были получены в «ручном» режиме подбора типа классификаторов в программе MatLab, могут быть расширены при переходе к автоматическому подбору классификаторов. В качестве дальнейших шагов в этом направлении целесообразно оценить разыгранную базу примеров, визуализировав ее в сокращенном признаковом пространстве, провести анализ критериев, влияющих на варианты развития предприятия. Использованный в работе прием для этой задачи, очевидно, реализуем и в других задачах менеджмента и экономики.

Заключение

Таким образом, в работе продемонстрировано применение методов машинного обучения с использованием программного продукта MatLab для выбора решений варианта развития компании. Показано, что наилучшую точность классификации показал метод опорных векторов, который рекомендован для использования в реальных ситуациях. Машинное обучение является составным элементом искусственного интеллекта, поэтому примененный в работе подход может служить начальным элементом при переходе к цифровой экономике.

В работе показано, что метод опорных векторов дает лучшую точность классификации, равную 98%, в задаче выбора варианта развития предприятия. Поставленная задача была решена на основе шести выбранных критериев, в качестве которых использовались прогноз развития рынка, обеспеченность ресурсами, конкурентоспособность, заинтересованность сторон, лояльность покупателей, эффективность компании. Дальнейшие исследования в этом направлении предполагают использование полученной модели в виде опорных векторов для ситуации, формирующейся на предприятии в конкретные временные промежутки, например, в начале или конце года. В этом случае менеджмент компании может принимать решение о выборе варианта дальнейшего развития предприятия, основываясь не только на субъективной оценке (опыт, знания, квалификация), но и применяя в качестве объективной оценки результат решения задачи, изложенной в статье.