Оценка эффективности труда методами машинного обучения

Введение

Измерение эффективности труда представляет собой сложную задачу. Ни одна управленческая проблема не привлекала столько внимания и не продвигалась к решению, как задача нахождения действенного и полезного метода измерения и оценки эффективности. Используемые в настоящее время способы часто не точны и не предлагают те виды решений, которые желает принимать организация. Из-за большого количества проблем, связанных с определением эффективности, многие руководители полагают, что лучший вариант – заменить комплексную оценку эффективности одним основным критерием, относительно свободным от предвзятости, – трудовым стажем. Хотя, на наш взгляд, это не совсем верно. Для преодоления трудностей при проведении оценки многие организации делают одну из двух ошибок: либо ничего не предпринимают, либо используют некорректные программы оценки, которые предоставляют оцениваемому сотруднику поверхностную конструктивную основу для улучшения поведения на рабочем месте.

В работе предлагается введение методов машинного обучения в процесс оценки эффективности труда. Применение такой технологии для поставленной задачи еще не очень распространено, но тем не менее укажем несколько работ из области управления персоналом, где используется машинное обучение [1] (Korablev, Bulatov, 2018). В хедж-фонде Bridgewater Associates создан тренер на основе искусственного интеллекта (ИИ) для своих сотрудников [2]. Алгоритм учитывает ряд показателей отдельного сотрудника: количество рабочих часов, успешных сделок, провалов, заработанных для клиентов денег, пиков активности, депрессии, изменение настроения и множество других факторов. На основе такого массива информации ИИ по-новому выдает рабочие рекомендации сотруднику. ИИ поможет совершать сделки самым эффективным способом. При этом система одновременно видит общую картину работы офиса: за счет кого эффективность падает, кто, наоборот, продвигает всех вперед.

Чаще всего машинное обучение в области управления человеческими ресурсами применяется при подборе кандидата на вакантную должность в фирме. Можно привести в качестве примера компанию Google [3]. Подход компании к поиску и найму талантов был однозначно успешным. Эта фирма использует аналитику для определения и снижения количества собеседований с «идеальными» кандидатами с десяти до пяти, что впоследствии сэкономило огромное количество времени и миллионы долларов. В [4] (Boselli, Cesarini, Mercorio, Mezzanzanica, 2017) рассмотрен подход к автоматической классификации миллионов вакансий в Интернете по стандартной таксономии профессий. Эта проблема оценена с точки зрения классификации текста, содержащего вакансии, посредством машинного обучения. В области развития персонала и обучения пока нет сформировавшейся точки зрения на то, как необходимо «обучать» сотрудников. На мировую отрасль обучения и развития потрачено более 200 млрд долл. США, но по крайней мере половина из этих средств были израсходованы напрасно: разработанные решения забыты, применяются ненадлежащим образом или просто являются тратой времени [5]. Необходимы алгоритмы, которые могли бы отслеживать и изучать знания, поведение и действия наиболее эффективных сотрудников команды и затем просто объяснять, что необходимо, чтобы им соответствовать. Подобные алгоритмы типа Netflix уже используются в сфере обучающих платформ, делая обучение столь же полезным и веселым, как просмотр кабельного телевидения.

Цель данной работы заключается в демонстрации методов машинного обучения для оценки эффективности труда работника. Статья далее структурирована следующим образом. Вначале, в основной части, описывается методология исследования, включающая основы машинного обучения и использованные при исследовании методы. Далее приводятся полученные результаты решения поставленной задачи с привлечением методов машинного обучения, выбора наилучшего метода и анализа найденных оценок. В заключении указываются главные выводы и намечаются пути дальнейшего исследования.

Методология

Машинное обучение

Машины по своей природе лишены интеллекта. Первоначально машины были разработаны для выполнения определенных задач, таких как движение по железной дороге, перемещение больших объемов грузов, копание глубоких ям, путешествие в космос и стрельба по движущимся объектам. Машины выполняют свои задачи намного быстрее и с более высоким уровнем точности по сравнению с людьми. Они сделали нашу жизнь более легкой. Принципиальная разница между людьми и машинами при выполнении своей работы заключается в интеллекте. Человеческий мозг получает данные, собранные пятью органами чувств: зрение, слух, запах, вкус и осязание. Эти собранные данные направляются в человеческий мозг через нейронную систему для восприятия и формирования действий.

Машинное обучение (machine learning) представляет собой подмножество методов ИИ, характерной чертой которых является не прямое решение задачи, а обучение в процессе решения. Основная проблема с использованием методов машинного обучения сводится к выработке решения по оценке принадлежности наблюдаемого объекта к тому или другому классу.

Под термином «машинное обучение» понимается технология, которая в [6] (Alpaydin, 2010) определена следующим образом: «Оптимизация критерия производительности модели с использованием данных и прошлого опыта». У нас есть модель, определенная с точностью до некоторых параметров, а обучение – это выполнение компьютерной программы для оптимизации параметров модели. Модель может быть прогнозирующей, чтобы делать прогнозы в будущем, или описательной – для получения знания из данных, или и того, и другого. В машинном обучении данные играют незаменимую роль, а алгоритм обучения используется для обнаружения и изучения знаний или свойств из данных. Качество или количество набора данных будут влиять на эффективность обучения и прогнозирования.

Чаще всего в менеджменте необходимо решать задачи классификации или регрессии. Укажем их формулировки.

Классификация. Алгоритму ставится задача определить категорию или класс, к которому частный пример принадлежит. Это делается путем обучения функции f: Rⁿ → {1, . . ., m}, которая отображает вектор признаков x в один конкретный класс из m различных классов.

Регрессия. При решении такой задачи алгоритм должен предсказать числовое значение по входным данным. Здесь алгоритм формирует функцию f: Rⁿ → R, которая определяет непрерывное значение y или набор непрерывных значений, выраженный как вектор y. Как видно, регрессия отличается от классификации форматом выхода.

Для решения проблемы на компьютере нужен алгоритм, который представляет собой последовательность инструкций для преобразования входных данных в выходное значение. Однако для некоторых задач нет алгоритма, например, при различении спама от нужных писем. В такой ситуации неизвестно, как преобразовать входные данные к выходу. Здесь и применим метод машинного обучения, так как он подходит для задач, связанных с интеллектом, в частности распознавания изображений и анализа речи, где физические законы или математические уравнения не способны дать модели.

То, чего нам не хватает в знаниях, мы восполняем в данных. Наша цель заключается в том, чтобы компьютер (машина) автоматически извлекал алгоритм для конкретной задачи. У нас есть много приложений, для которых нет алгоритма, но есть примеры данных.

Мы хотим запрограммировать компьютеры таким образом, чтобы они могли «учиться» на основе доступного им ввода. Грубо говоря, обучение – это процесс преобразования опыта в знания [7] (Kim, 2017). Вход в алгоритм обучения – обучающая выборка (training data), представляющая опыт, а выход – некоторые знания, обычно принимающие форму другой компьютерной программы для выполнения какой-то задачи. Процесс машинного обучения формирует модель из обучающих данных, а затем эта модель применяется к фактическим полевым данным. Такая процедура проиллюстрирована на рисунке 1.

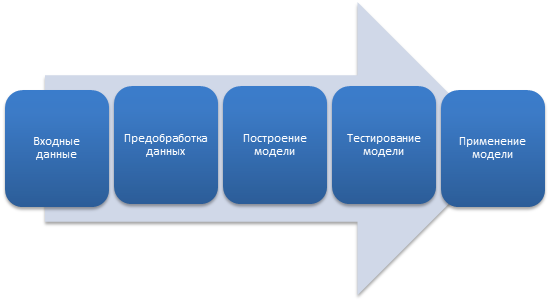
Рисунок 1. Обучение и применение модели машинного обучения Источник: составлено авторами.

Далее кратко описаны некоторые методы машинного обучения, которые используются в этой работе.

Метод главных компонентов

Метод главных компонентов (ГК) представляет собой статистический метод снижения размерности. Основная идея метода ГК заключается в уменьшении размерности первоначального набора данных, в котором имеется большое количество взаимосвязанных переменных, сохраняя при этом как можно большую долю дисперсии исходных данных [8, 9] (Jolliffe, 2002). Это снижение достигается путем перехода к новому набору показателей – главным компонентам, которые некоррелированы и упорядочены таким образом, что первые несколько ГК сохраняют большую часть дисперсии, характеризующую исходные данные. Вычисление ГК сводится к нахождению собственных чисел и собственных векторов для положительной полуопределенной симметричной матрицы. Таким образом, определение и нахождение ГК с вычислительной точки зрения достаточно прямолинейно, но этот простой метод имеет широкий спектр различных применений.

Кроме того, при сохранении двух или трех ГК реализуется возможность визуализации многомерных объектов в сокращенном признаковом пространстве. Метод ГК обладает рядом свойств, делающих его эффективным для визуализации структуры многомерных данных. Все они касаются наименьшего искажения геометрической структуры точек (объектов) при их проектировании в пространстве меньшей размерности.

Деревья решений

Деревья решений являются одним из наиболее популярных подходов к решению задач добычи данных. Они создают иерархическую структуру классифицирующих правил типа «ЕСЛИ…ТО…» (if-then), имеющую вид дерева [10, 11] (Hastie, Tibshirani, Friedman, 2009). Чтобы принять решение, к какому классу следует отнести некоторый объект или ситуацию, требуется ответить на вопросы, стоящие в узлах этого дерева, начиная с его корня. Вопросы имеют вид «значение параметра А больше В?». Если ответ положительный, осуществляется переход к правому узлу следующего уровня. Затем снова следует вопрос, связанный с соответствующим узлом, и т. д. Приведенный пример иллюстрирует работу так называемых бинарных деревьев решений, в каждом узле которых ветвление производится по двум направлениям (т. е. на вопрос, заданный в узле, имеется только два варианта ответов, например Да или Нет). Однако в общем случае ответов и, следовательно, ветвей, выходящих из узла, может быть больше.

Деревья классификации дают номинальные ответы, например «истина» или «ложь», метку класса. Деревья регрессии дают числовые ответы на заданные входные данные. Каждый шаг включает проверку значения одного предиктора (переменной). Такие методы концептуально простые, но мощные.

При данном входе на каждом узле проверяется тест и в зависимости от результата выбирается одна из ветвей. Этот процесс начинается с корня и повторяется рекурсивно до тех пор, пока не будет обнаружен листовой узел, после чего значение, записанное в листе, определяет выход.

Метод опорных векторов

Метод опорных векторов (Support Vector Machines) выполняет классификацию путем построения N-мерной гиперплоскости, которая оптимально разделяет данные на две категории. Принципиально всегда возможно преобразовать любое множество данных таким образом, чтобы классы могли быть линейно разделены. Перспективный метод для построения разделяющих функций в задаче классификации или оценки функций в регрессионном анализе связан с теорией метода опорных векторов (МОВ). Такой подход основан на статистической теории обучения, которая играет ключевую роль во многих областях техники, медицины, экономики.

Модели этого метода близки к нейронным сетям. На самом деле модель МОВ с использованием сигмоидной функции ядра эквивалентна персептрону, состоящему из двух слоев нейронов. МОВ предназначен для решения задач классификации путем поиска хороших решающих границ, разделяющих два набора точек, которые принадлежат разным категориям [12, 13] (Vapnik, 1998; Cristianini, Shawe-Taylor, 2003). Для классификации новых точек достаточно проверить, по какую сторону от границы они находятся.

В МОВ поиск решающих границ осуществляется в два этапа:

1. Данные отображаются в новое пространство более высокой размерности, в котором граница может быть представлена как гиперплоскость.

2. Решающая граница вычисляется путем максимизации расстояния от гиперплоскости до ближайших точек каждого класса. Такое действие дает возможность обобщить классификацию новых образцов, не относящихся к обучающему набору.

Алгоритм обучения МОВ строит модель, которая относит новые примеры в одну или другую категории.

В простейшем случае задач распознавания МОВ используют линейную разделяющую плоскость для создания классификатора с максимальным отступом. Для выполнения этого обучающая проблема рассматривается как нелинейная оптимизационная задача с ограничениями. В такой постановке функция стоимости – квадратичная, а ограничения – линейные, т.е. необходимо решить квадратичную задачу программирования.

Метод ближайшего соседа

Классификация методом ближайшего соседа (k-Nearest Neighbor, или k-NN), представляет собой алгоритм машинного обучения, который локализует группу из k объектов в обучающей выборке, находящуюся ближе всего к тестовому объекту.

Модель для k-NN – это весь набор обучающих данных. В процессе обучения алгоритм начинает классификацию только в той ситуации, когда появляются новые неразмеченные данные. Для этого алгоритма необходимы три важных компонента [14–16] (Coppin, 2007; Kotsiantis, 2007; Zhang, Li, Zhang, 2017):

· группа размеченных объектов;

· метрика близости;

· число k ближайших соседей.

При появлении новых данных работа алгоритма k-NN представляет собой последовательность следующих шагов:

1. Определяются k ближайших соседей.

2. С использованием классов соседей алгоритм решает, как лучше классифицировать новые данные.

При сформированном списке k ближайших соседей новые объекты классифицируются в соответствии с принципом большинства. Новую точку данных включают в тот класс, к которому относится наибольшее количество соседей.

Дискриминантный анализ

В машинном обучении ДА применяется для нахождения линейной комбинации признаков, которая характеризует или разделяет два или более класса объектов или событий. Результирующее уравнение может быть использовано в качестве линейного классификатора. ДА стремится максимизировать разделение между классами данных и формирует ровно столько же линейных функций, сколько классов имеется в данных [17]. Предсказанный класс для очередного наблюдения будет тот, который имеет самое высокое значение для линейной функции.

Предполагается, что различные классы генерируют данные на основе разных распределений Гаусса. ДА находит набор прогнозных уравнений, основанных на независимых переменных, которые используются для классификации объектов в группы. Выполнение ДА преследует две цели:

· найти уравнение для классификации новых объектов;

· интерпретировать уравнение для лучшего понимания отношений,

существующих среди переменных.

По существу, ДА стремится максимизировать разделение (дискриминацию) и производит ровно столько же линейных функций, сколько классов. Предсказанным классом для нового наблюдения будет тот, который имеет самое высокое значение для его линейной функции.

Подход, основанный на дискриминации, делает допущение о форме разделения между классами и не требует знаний о плотностях вероятности, например, являются ли они гауссовыми, коррелированы ли входы и т.д.

Результаты

При оценке эффективности труда работника положим, что факторами, в наибольшей степени влияющими на этот выходной показатель, являются следующие: Х1 – образование; Х2 – возраст; Х3 – опыт работы; Х4 – мотивация; Х5 – вовлеченность; Х6 – обучаемость. Примем также категорийную оценку эффективности: высокую, среднюю, низкую. Воспользуемся методом Монте-Карло для формирования синтетической выборки данных. Разыгранный этим методом набор данных представляет собой матрицу, состоящую из 7 столбцов (6 исходных факторов плюс категория) и 60 строк, определяющих по 20 наблюдений для каждой из трех категорий. При генерации факторов допустили, что каждый из них распределен по равномерному закону в диапазоне от 0 до 10 баллов (для признаков Х1, Х4–Х6) и в годах (для признаков Х2, Х3).

Метод ГК позволяет сократить размерность пространства признаков, совершая в рассматриваемом случае переход от 6 исходных признаков до двух агрегированных показателей. На рисунке 2 показаны все 60 наблюдений-строк исходной матрицы данных, представленных в плоскости первых двух ГК.

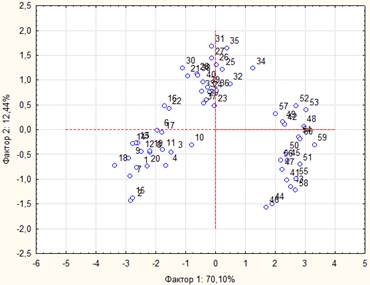
Рисунок 2. Наблюдения в плоскости первых двух ГК

Источник: получено авторами.

Потеря информации при таком переходе определяется через собственные числа матрицы корреляций исходных признаков. На графике рисунка 3 (график каменистой осыпи) показан ход изменения собственных чисел матрицы корреляций исходных данных.

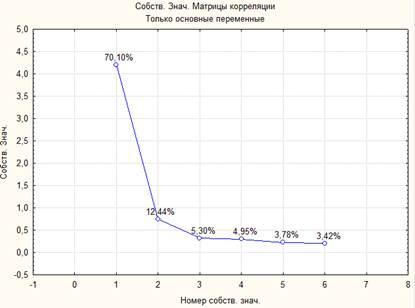
Рисунок 3. График каменистой осыпи

Источник: получено авторами.

Из приведенного графика видно, что при сохранении только двух собственных чисел (визуализация на плоскости) мы сохраняем 82% процента информации. При потере, равной 18%, мы приобретаем возможность рассмотреть наши многомерные объекты на плоскости.

Далее посредством модуля Classification Learner были выбраны несколько моделей классификаторов, которые обучались на исходной выборке данных. Результаты использования этих методов показаны на рисунке 4.

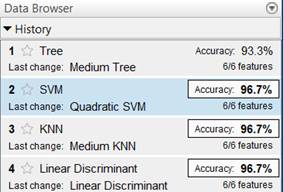
Рисунок 4. Результаты классификации

Источник: получено авторами.

Как видно из рисунка 4, у трех методов достигнута достаточно высокая и одинаковая точность классификации, что объясняется расположением смоделированных данных трех категорий: на рисунке 2 отчетливо видны три группы данных, практически не пересекающиеся. Вследствие этого достигнута такая высокая точность классификации. Выберем модель № 2 – метод опорных векторов – и для этой модели проанализируем полученные результаты.

На рисунке 5 показан график наблюдений, участвующих в обучении в плоскости первого и второго предикторов, и неправильные результаты, отмеченные крестиком.

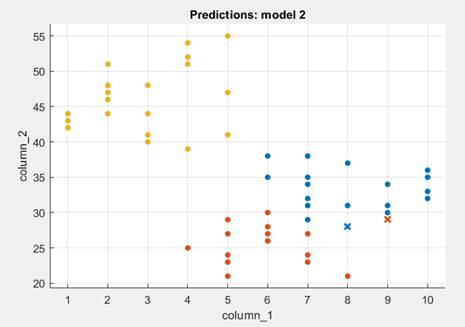
Рисунок 5. График наблюдений

Источник: получено авторами.

Как видно из графика, здесь всего 2 ошибки (два крестика на графике), причем данные третьего класса эффективности (в левом верхнем углу) классифицированы безошибочно.

Подтверждением этому служит матрица ошибок, показанная на рисунке 6.

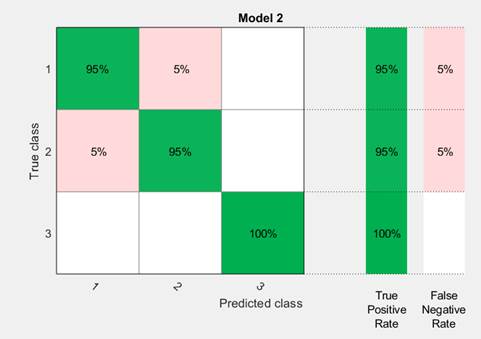
Рисунок 6. Матрица ошибок

Источник: получено авторами.

Здесь матрица ошибок приведена с добавлением «Доли верных положительных классификаций» ( True Positive Rates – TPR) и «Доли ложных отрицательных классификаций» (False Negative Rates – FNR), размещенных в правой части рисунка. В последних двух столбцах справа показаны сводные данные по каждому классу, откуда видно, что объекты только третьего класса разделены безошибочно: для него значения TPR = 100%.

На рисунке 7 приведена кривая операционной характеристики, которая показывает долю верных положительных классификаций (TPR) в функции от доли ложных положительных классификаций (false positive rate – FPR) для выбранного классификатора. Маркер показывает значения FPR и TPR для выбранного в данный момент классификатора. Например, величина FPR, равная 0,03, указывает на то, что текущий классификатор неправильно присваивает 3% наблюдений положительному классу (при построении операционной характеристики в качестве положительного класса выбран первый, остальные – отрицательные). Параметр AUC в данном случае практически равен 1, что говорит о высоком качестве классификатора.

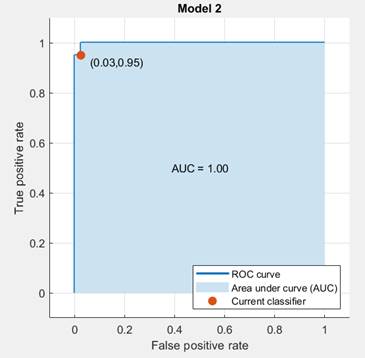
Рисунок 8. Операционная характеристика

Источник: получено авторами.

Сформированная структура trainModel используется для прогнозирования с использованием новых данных. В качестве примера ниже приведен результат классификации нового вектора x3 = [4 50 3 3 4 1]:

>> yfit = trainedModel.predictFcn(x3)

yfit =

3,

т.е. классификатор в виде метода опорных векторов отнес это наблюдение к категории 3 по эффективности труда. Переводя вектор наблюдений на реальные показатели, получили, что работник с образованием, оцениваемым в 4 балла, возрастом в 50 лет, но с малым опытом работы в этой сфере и достаточно низкими показателями мотивации, вовлеченности и обучаемости, относится к третьей (самой низкой) категории эффективности.

Заключение

В итоге в работе продемонстрировано использование методов машинного обучения для решения задачи по оценке эффективности труда работников. Хотя задача решена на смоделированных данных, было показано, что в такой области управления человеческими ресурсами могут использоваться сложные современные методы обработки данных, приводящие к важным результатам. В дальнейшем предполагается использовать для решения подобной задачи подход с применением нечеткой логики, что позволит получить оценку эффективности, выраженную в количественной форме.