Методы машинного обучения при оценке конкурентоспособности предприятия

1. Введение

Анализ и исследование понятия «конкурентоспособность» приводят к выводу, что пока еще не сложилось общепринятого определения этого термина. Любой аналитик обращает внимание на разные аспекты конкуренции, рассматривает различные трактования данного понятия. Все это приводит к наличию многообразных определений одного и того же понятия. В целом конкурентоспособность (КСП) понимают, прежде всего, как способность конкурировать, удерживать позиции на рынке, как свойство субъектов и результатов конкурентных отношений [1] (Zhdanova, 2015). Оценивая КСП на уровне стран, отраслей, предприятий, продукции, следует учесть, что страны, отрасли, товары не конкурируют сами по себе, в основе лежит деятельность предприятий с их экономическими интересами.

В отношении КСП различных стран уже выработалась определенная точка зрения. Индекс глобальной конкурентоспособности (Global Competitiveness Index) – это глобальное исследование и сопровождающий его рейтинг стран мира по показателю экономической КСП, который рассчитывается по методике Всемирного экономического форума (World Economic Forum) [2]. Этот подход основан на комбинации статистических данных и результатов опроса руководителей крупнейших мировых компаний. Подобное исследование проводится с 2004 года и на данный момент представляет наиболее полный комплекс показателей КСП по различным странам мира. Индекс интегрирует хорошо зарекомендовавшие себя аспекты с новыми и возникающими рычагами, которые стимулируют производительность и рост. В нем подчеркивается роль человеческого капитала, инноваций, устойчивости и гибкости, которые являются не только движущими силами, но и определяющими чертами экономического успеха в мире.

Индекс глобальной конкурентоспособности составлен из большого числа переменных, которые детально характеризуют КСП стран мира, находящихся на разных уровнях экономического развития. Все переменные объединены в 12 контрольных показателей, определяющих национальную КСП, в том числе качество институтов, инфраструктуру, макроэкономическую стабильность, здоровье и образование, эффективность рынка товаров и услуг и т.д.

Совсем иначе обстоит дело с КСП предприятий. Большое количество определений этого термина КСП, разъяснений его сущности не позволяют однозначно выявить факторы, которые оказывают наибольшее влияние на КСП. Например, среди факторов КСП, контролируемых организацией, укажем следующие [3]: уровень качества продукции; предпродажное и послепродажное обслуживание, наличие сервисных центров; квалификация персонала компании; имидж компании и т.п. Наличие значительного числа публикаций в области КСП предприятий все же не позволяет придти к однозначному выводу о факторах и типах КСП, методах классификации КСП [4-6] (Zelga, 2017; Shpak, Seliuchenko, Kharchuk, 2019). Из изложенного следует цель настоящей работы, заключающаяся в применении методов машинного обучения к классификации КСП предприятий.

Далее работа структурирована следующим образом: вначале дается краткое описание принципов машинного обучения и методов, пригодных для решения поставленной задачи; затем анализируются полученные результаты для классификации КСП; в итоге указываются пути дальнейших работ.

2. Методология

Машинное обучение и его инструменты

Машинное обучение (МО) представляет собой метод моделирования, который включает данные [7, 8]. Это определение может показаться слишком кратким, но, по существу, МО – это метод, который определяет модель из данных. Здесь под данными подразумевается такая информация, как документы, аудио, изображения и т.д. Модель является конечным продуктом МО.

Машинное обучение использует теорию статистики при построении математических моделей, потому что основной задачей является формирование вывода из выборки данных. Роль компьютерных наук двойственная. Во-первых, в обучении нужны эффективные алгоритмы для решения задачи оптимизации, а также для хранения и обработки огромного количества данных, которые обычно имеются. Во-вторых, как только модель изучена, ее представление и алгоритмическое решение для вывода также должны быть эффективными. В некоторых приложениях эффективность алгоритма обучения или логического вывода, а именно его пространственная и временная сложность, может быть столь же важной, как и его точность прогнозирования.

Само название МО отражает тот факт, что описываемый метод анализирует данные, и он сам, а не человек, находит модель. Этот процесс называется «обучением», потому что он напоминает обучение с данными для поиска модели. Следовательно, данные, которые используются при МО, являются обучающими данными.

Алгоритм k-NN

Алгоритм k-ближайших соседей (k-nearest neighbors – k-NN) представляет собой контролируемый алгоритм МО, который используется для решения задач классификации. При выполнении этого метода предполагается, что подобные объекты располагаются рядом друг с другом. Алгоритм k-NN отражает идею сходства, иногда называемую расстоянием или близостью, и сводится к вычислению расстояния между точками на графике [9, 10] (Ezghazi, Zahi, Zekoua, 2017).

В этом методе входные данные состоят из k ближайших обучающих примеров в пространстве признаков. Выходные данные зависят от того, используется ли алгоритм k -NN для классификации или регрессии. При классификации выходные данные являются членами класса. Объект классифицируется множеством голосов его соседей, при этом объект присваивается классу, наиболее распространенному среди его k ближайших соседей (k является положительным целым числом, обычно небольшим). Если k = 1, то объект просто присваивается классу этого единственного ближайшего соседа.

На этапе классификации параметр k является определяемой пользователем константой, а неотмеченный вектор (точка запроса или контрольная точка) классифицируется путем назначения метки, которая наиболее часто встречается среди k обучающих выборок, ближайших к этой точке запроса. Обычно используемая метрика расстояния для непрерывных переменных – евклидово расстояние.

Для нового экземпляра прогнозы о принадлежности к классу делаются путем поиска во всем обучающем наборе k наиболее похожих экземпляров (соседей) и суммирования выходной переменной для этих k экземпляров.

Деревья решений

Деревья решений используются для предсказания размещения классов или объектов в категории по результатам измеряемых параметров [11, 12] (Azad, Moshkov, 2017; Kim, Hong, 2017). Обычно поиск решения – реализация методов для выполнения бинарной классификации путем расщепления ветвей дерева, основываясь на измеренных значениях предикторов. В таких деревьях листья представляют метки классов, а ветки представляют конъюнкции признаков, которые ведут в эти метки классов. Конечный узел содержит ответ. При классификации деревья дают ответы, которые являются номинальными, такими как «истина» или «ложь».

Деревья классификации широко используются при установлении диагноза пациента, формировании структуры данных, принятии решений. Графический вид результатов позволяет улучшить их интерпретацию. Цель формирования деревьев решений сводится к предсказанию значений зависимой переменной в функции от соответствующих значений одной или нескольких независимых переменных (предикторов).

Нейронные сети

Нейронная сеть – это «черный ящик», который отражает ситуацию с полностью неизвестным процессом, но в наличии есть наблюдения (примеры). Здесь известны входы и выход, но требуется база примеров, по которой обучается сеть. В общем случае НС представляет собой машину, моделирующую способ обработки мозгом конкретной задачи [13] (Haykin, 2009). Такая сеть реализуется с помощью электронных компонентов или моделируется программой, выполняемой на компьютере. Благодаря своим возможностям обучения и обобщения нейронные сети могут быть выражены как математическое отображение архитектуры мозга человека.

Поясним принцип нейросетевой технологии на однослойной сети с R входами и S нейронами в слое (рис. 1). В этой сети каждый элемент входного вектора р соединен с каждым входным нейроном через матрицу весов W. Нейрон с индексом i имеет сумматор, на который поступают взвешенные входы и смещения для формирования i-го скалярного выхода n(i). Различные n(i) объединяются вместе, образуя S-й элемент входного вектора n, которые являются аргументами функции активации f. В итоге на выходе сети формируется выходной вектор-столбец а.

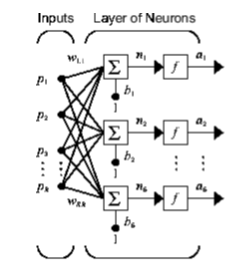
Рисунок 1. Однослойная сеть с R входными элементами

Источник: [14]

3. Результаты

В качестве факторов, влияющих на КСП предприятия, примем следующие:

1) качество выпускаемой продукции;

2) товарно-сбытовая деятельность предприятия;

3) организационно-техническое совершенство производства;

4) финансовое состояние;

5) имидж предприятия.

Такой набор факторов, по мнению автора, является достаточным для целей исследования, так как он охватывает основные аспекты КСП и не противоречит общепринятым тенденциям [3, 4] (Zelga, 2017).

Классы КСП организации установим такими [4] (Zelga, 2017):

1) нормальная (normal) – результаты конкретных взаимодействий совпадают с ожиданиями участвующих заинтересованных сторон;

2) ниже нормальной (less) – фактические результаты не соответствуют ожиданиям. Затем заинтересованные стороны, вовлеченные в эту ситуацию, предпримут действия, чтобы отказаться от взаимодействия с компанией и перейти к другой, более привлекательной;

3) выше нормальной (more) – фактические результаты выше, чем ожидалось. Заинтересованные стороны, у которых есть основания для таких оценок, стремятся укрепить свои отношения с компанией.

Для создания базы примеров, которая используется в МО при формировании модели, возможно использование двух подходов:

· применение реальных данных;

· использование «игрушечных» наборов данных.

В проводимом исследовании реальных данных еще нет, поэтому обратимся ко второму приему. В МО важно научиться правильно применять игрушечные наборы данных [15, 16] (Ramsundar, Zade, 2019; Shakla, 2019), так как обучение алгоритма на реальных данных сопряжено с трудностями и может закончиться неудачей. Игрушечные наборы данных играют решающую роль для понимания работы алгоритмов. При наличии простой синтетической выборки данных достаточно просто оценить, обучился алгоритм нужному правилу или нет. На реальных данных получить такую оценку сложно. Здесь воспользуемся методом Монте-Карло для формирования синтетической выборки данных. При розыгрыше примем для каждого фактора диапазон от 0 до 10 баллов с учетом классов и дополним результаты моделирования случайным шумом. Каждый разыгранный класс имеет по 10 строк, и вся таблица представляет собой матрицу размером 30*5. Фрагмент разыгранных данных показан в таблице 1.

Таблица 1

Фрагмент разыгранных данных

На рисунке 2 в плоскости первых двух переменных (качество продукции и товарно-сбытовая деятельность) представлены все 30 смоделированных объектов, каждый из которых характеризуется определенной величиной КСП.

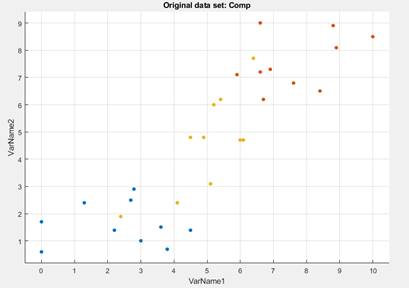
Рисунок 2. Исходные данные

Источник: получено автором.

Далее на основе такой таблицы необходимо проанализировать различные методы классификации и выбрать тот из них, который покажет лучшую точность. Для решения этой задачи воспользуемся программным продуктом MatLab 2018b. В этой версии программы имеется специальный модуль Classification Learner, открывающий более широкие возможности построения классификаторов по сравнению с более ранними версиями. Этот модуль может работать в ручном режиме (manual), когда поочередно проверяется тот или иной метод, и автоматическом (automated), когда программа просматривает все возможные решения для данной задачи и указывает лучшие результаты. Напомним, что методы МО на основе имеющихся данных формируют модель, которая может использоваться для классификации новых наблюдений. Здесь применим автоматический режим, в котором выберем опцию All Quick-To-Train. Эта опция для нашего набора данных обучит все те модели, которые являются наиболее быстрыми.

Результаты этой процедуры показаны на рисунке 3, где среди 9 проанализированных методов наивысшую точность продемонстрировал метод № 1.5 (medium k-NN).

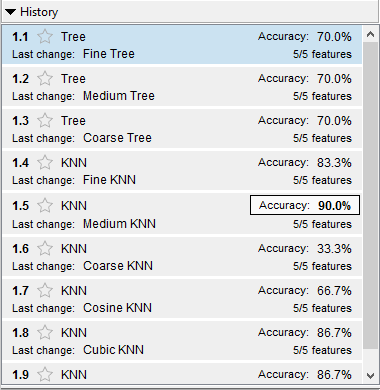
Рисунок 3. Результаты подбора модели

Источник: получено автором.

Приведем результаты для выбранного программой метода. На рисунке 4 представлена матрица ошибок для метода k-NN . Строками матрицы ошибок являются истинные классы, столбцами – предсказанные. Диагональные элементы показывают, где истинный и предсказанный классы совпадают. Сумма всех чисел в ячейках матрицы составляет 30, т.е. равняется числу объектов. Как видно из матрицы, обученный классификатор ошибался на объектах класса normal: перепутал его с классом more (1 раз) и классом less (2 раза).

На рисунке 5 показана матрица ошибок с добавлением «Доли верных положительных классификаций» ( True Positive Rates – TPR) и «Доли ложных отрицательных классификаций» (False Negative Rates –FNR), размещенных в правой части рисунка.

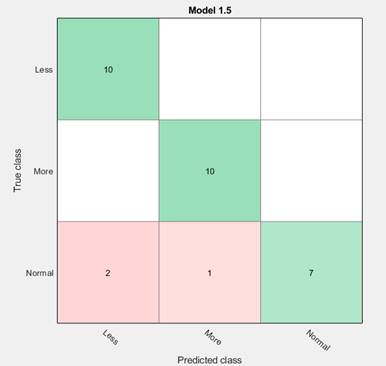
Рисунок 4. Матрица ошибок

В последних двух столбцах справа показаны сводные данные по каждому классу. Например, в третьей строке для класса normal стоят значения 70 % и 30 %, соответствующие TPR и FNR. Иными словами, для этого класса доля правильно расклассифицированных объектов составляет 70 %, а доля ошибочных – 30 %. Также видно, что объекты первого и второго классов разделены безошибочно: для них значения TPR = 100 %.

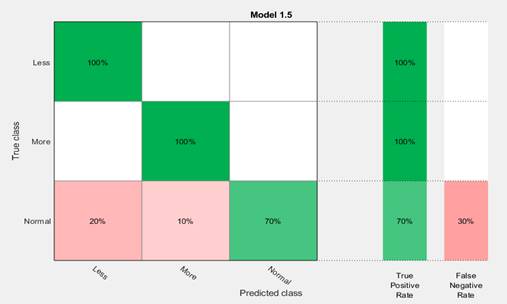
Рисунок 5. Положительные и отрицательные классификации

На рисунке 6 показана кривая операционной характеристики (receiver operating characteristic – ROC), которая показывает долю верных положительных классификаций (TPR) в функции от доли ложных положительных классификаций (false positive rate – FPR) для выбранного классификатора.

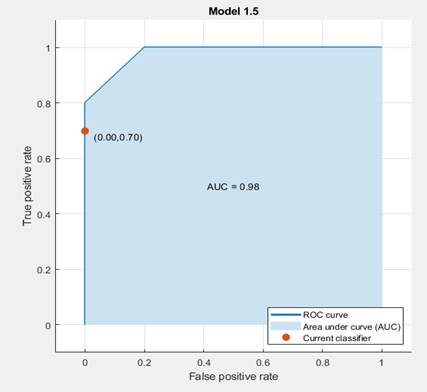
Рисунок 6. Кривая операционной характеристики

На приведенном графике идеальный результат безошибочной классификации – это линия, образующая прямой угол в верхнем левом углу графика. Плохой результат, который не лучше случайного, отображается линией, проходящей под углом 45 градусов из левого нижнего угла графика в правый верхний. Число, характеризующее площадь под кривой (Area Under Curve – AUC), является показателем общего качества классификатора. Чем больше значения AUC, тем лучше качество классификатора.

Для предсказания класса нового наблюдения необходимо после создания модели экспортировать ее в рабочую область. В итоге формируется структура trainModel, которая используется для прогнозирования с использованием новых данных. В качестве примера ниже приведен результат классификации нового вектора mj1 = (2.8 2.9 0.4 2.3 2.5):

>> yfit = trainedModel.predictFcn (mj1)

yfit =

categorial

Less

Таким образом, выбранный метод k-NN отнес КСП данного объекта к классу, который обозначен как «ниже нормальной КСП».

Обратимся к нейронной сети (НС) для классификации КСП разыгранных объектов. Хотя НС и не выбрана в автоматическом режиме как приемлемый классификатор (была выбрана опция All Quick-To-Train, нацеленная, прежде всего, на скорость вычислений). Созданная в программе MatLab двухслойная нейронная сеть с выбранным количеством нейронов, соответствующих задаче, приведена на рисунке 7.

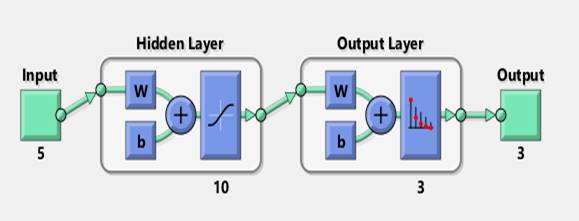
Рисунок 7. Нейронная сеть

Источник: получено автором.

Исходная совокупность данных из 30 объектов делится на 3 части в пропорции 70 %, 15 % и 15 %:

· обучающая (Training) выборка (20 объектов), которая используется для обучения сети;

· валидационная (Validation) выборка (5 объектов), применяемая для оценивания обобщающей способности сети и остановки процесса обучения в случае прекращения улучшения обобщения;

· тестовая (Testing) выборка (5 объектов), предназначенная для независимой меры характеристики сети во время и после обучения.

Часть результатов обучения представлена ниже. На рисунке 8 приведены три кривые обучения, соответствующие обучающей, валидационной и тестовой выборкам.

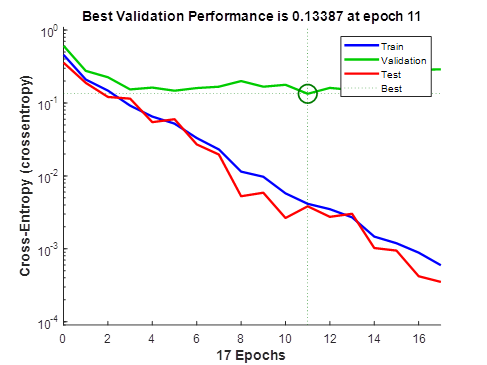
Рисунок 8. Кривые обучения сети

Источник: получено автором.

На вертикальной оси графика рисунка 8 отложена величина кросс-энтропии (cross-entropy), которая оценивает поведение сети с учетом целевых и выходных значений. Минимизация кросс-энтропии приводит к классификаторам хорошего качества. На горизонтальной оси указано количество эпох обучения, откуда видно, что на 11 эпохе произошло ухудшение обобщения сети, поэтому сеть обучилась за это время.

Для определения принадлежности предприятия-объекта с конкретному классу из 3 выделенных сохраним нейронную сеть в рабочем пространстве MatLab, а затем подадим на ее вход через командное окно параметры объекта, например, mj3 = [5.5; 6.5; 5; 5; 6].

Сеть выдает ответ в виде вектора столбца, наибольшее значение которого определяет класс:

>> fit = net (mj3)

fit =

0.0001

0.9990

0.0009.

Таким образом, с помощью нейронной сети для конкретного примера получили ответ о принадлежности объекта с такими параметрами ко второму классу (в наших обозначениях – normal).

4. Обсуждение

Полученные результаты показывают возможность применения методов машинного обучения для оценивания конкурентоспособности предприятий. Все расчеты выполнены на основе разыгранной базы данных. В реальной ситуации и сами факторы, и их значения могут быть отличными от рассмотренных в данной работе, но здесь и не преследовалась цель создания расчетной методики для оценки конкурентоспособности. Рассматривался лишь подход для классификации конкурентоспособности с использованием методов машинного обучения.

Заключение

Таким образом, в работе продемонстрировано применение методов машинного обучения с использованием программного продукта MatLab 2018b для решения задачи по конкурентоспособности предприятий. В дальнейшем предполагается проанализировать возможности формирования количественной оценки конкурентоспособности предприятий.