Методика анализа и прогнозирования показателей развития малых предприятий в регионах ЮФО с помощью нечеткого моделирования

Данные о реальных экономических процессах, необходимые для их анализа и моделирования, часто являются неточными, могут поступать нерегулярно, иногда их достоверность вызывает сомнения. Чаще всего не удается собрать всю информацию об исследуемых факторах, влияющих на эти процессы. В таком случае оправданным является использование нечетких моделей и методов.

В данной работе для анализа и прогнозирования показателей развития малых предприятий в регионах Южного федерального округа (ЮФО) применен один из таких методов – метод нечеткой линейной регрессии, реализованный на языке Python.

Введем следующие обозначения:

Y– число малых предприятий на 10 000 человек населения;

Х₁ –валовой региональный продукт на душу населения (руб.);

Х₂ – инвестиции в основной капитал на душу населения в регионе (руб.);

Х₃ – уровень занятости в регионе (в процентах).

Для иллюстрации предложенного метода оценим влияние важнейших экономических показателей регионов Южного федерального округа на основе данных за 2010–2018 гг., взятых из [1].

В методе нечеткой линейной регрессии используются симметричные треугольные нечеткие числа. Такое число A задается тройкой чисел , a и , где

. (1)

Если знаки неравенств (1) строгие, то нечеткое число а имеет следующую функцию принадлежности:

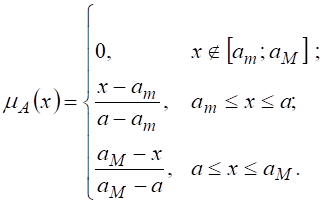
При выполнении условия , где , число A=< , , ˃, называется симметричным.

Задачу нечеткой линейной регрессии можно сформулировать следующим образом. Для имеющихся k результатов наблюдений зависимой переменной от n факторов , где i=1,…,n, нужно найти коэффициенты (нечеткие числа) A₀, A₁, …, A_n, такие, чтобы выполнялись условия µ_j(Y_j)≥ h, где µ_j(Y_j) – функция принадлежности нечеткого множества , величина h – заданный порог надежности, причем неопределенность, связанная с этими коэффициентами, была бы минимальной. Пусть параметрами модели являются числа А_i = < a_i–r_i, a_i, a_i+r_i>, где и . Заметим, что – также треугольное нечеткое число. Чтобы найти, a_{i и} r_i, необходимо решить задачу линейного программирования [2–4] (Tanaka, Uejima, Asai, 1982; Volkova, Gisin, 2015; Bogachev, Alekseychik, Pushkar, 2019):

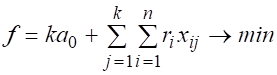(2)

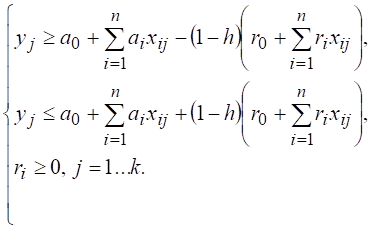
Для каждого из рассматриваемых регионов построим модели при пороге надежности, например h = 0,5, используя наблюдаемые значения выбранных показателей за 2010–2017 гг. При этом значения показателей 2018 г. используются для проверки построенной модели на качество прогноза. Тогда для нахождения a_i и r_i в соответствии с (1) и (2) получаем задачу линейного программирования:

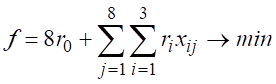(3)

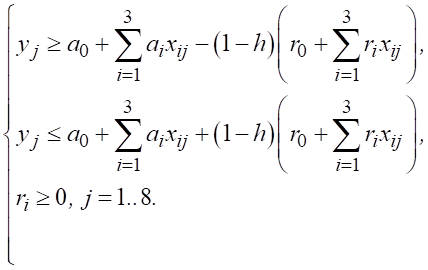
Задача (3) решается с помощью современных программных средств [5, 6].

При решении задачи (3) для Ростовской области получено следующее уравнение нечеткой регрессии:

В построенной модели нечетким является только параметр при показателе «Уровень занятости в регионе» (Х₃), причем он имеет и больший вес в полученной регрессии. Показатели Х₁ «Валовой региональный продукт на душу населения» и Х₂ «Инвестиции в основной капитал на душу населения в регионе» практически не оказывают влияния на исследуемый показатель. Значительная величина свободного члена может объясняться влиянием недостающих факторов.

Заметим, что Y = <Y_d, Y_m, Y_u>, где Y_m отражает модальное значение показателя Y, Y_d – пессимистический прогноз этого показателя, Y_u – оптимистический прогноз. На рисунке 1 представлен график нечеткой линейной регрессии вместе с наблюдаемыми значениями Y, который отражает нечеткий прогноз для исследуемого показателя.

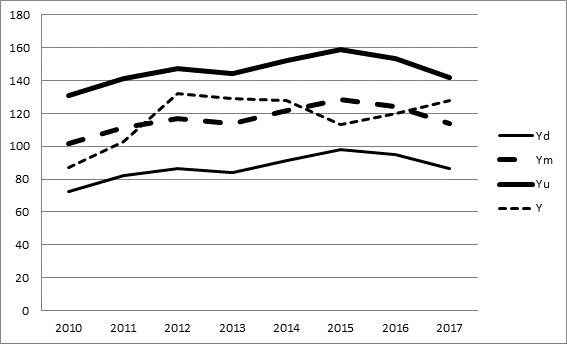
Рисунок 1. График нечеткой линейной регрессии для показателя числа малых предприятий на 10 000 чел. населения в Ростовской области, h = 0,5

Как следует из графика, с 2010 г. по 2013 г. фактические значения числа малых предприятий на 10 000 чел. населения соответствуют направленности оптимистического прогноза. В 2014 г. и 2016 г. значения этого показателя совпали с его модальными значениями. В 2015 году число малых предприятий этого региона в большей степени приближается к пессимистическому прогнозу, а в 2017 году – к оптимистическому прогнозу показателя. Очевидно, что в Ростовской области в исследуемом периоде наблюдается достаточно стабильное развитие числа малых предприятий, что подтверждается и прогнозным значением показателя в 2018 году (табл. 1).

Оценка результатов исследования влияния факторов Х₁, Х₂, Х₃ на число малых предприятий на 10 000 человек населения в Ростовской области выполнена с помощью значения показателя в последующем, 2018 г. (табл. 1).

Таблица 1

Оценка результатов исследования Ростовской области для модели с порогом надежности 0,5

Как видно из таблицы 1, уравнение нечеткой линейной регрессии построено достаточно корректно и может быть использовано для прогноза.

Проведем аналогичное исследование для Республики Адыгея.

Уравнение нечеткой регрессии при h = 0,5 для этого региона имеет вид:

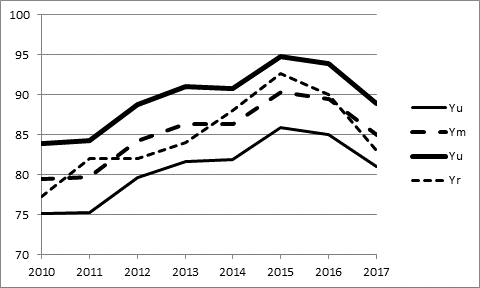
Рисунок 2. График нечеткой линейной регрессии для показателя числа малых предприятий на 10 000 чел. населения в Республике Адыгея, h = 0,5

Так же, как и в Ростовской области, нечетким параметром модели регрессии является только коэффициент при показателе «Уровень занятости в регионе (Х₃)», оказывающий большее влияние на исследуемый показатель, чем валовый региональный продукт и инвестиции в основной капитал на душу населения в регионе, которые практически не играли большой роли в развитии числа малых предприятий в исследуемом периоде. Сравнительно большая величина свободного члена может быть объяснена, например, влиянием недостающих факторов.

Как следует из графика (рис. 2), исследуемый показатель достаточно близок к модальному значению. До 2015 года наблюдается достаточно слабое развитие числа малых предприятий, а с 2015 года в регионе имеет место достаточно плавное его снижение до уровня 2010 года. Для выяснения причин таких изменений необходимы дополнительные исследования.

Несколько другие результаты получены при проведенном аналогичном исследовании для Краснодарского края.

Уравнение нечеткой регрессии при h = 0,5 для этого региона имеет вид:

В этом уравнении параметры при показателях Х₁ и Х₃ являются нечеткими, а свободный член и коэффициент при показателе Х₂ равны нулю.

Следовательно, показатель Х₂ – инвестиции в основной капитал на душу населения в регионе не оказывает большого влияния на исследуемый показатель. Достаточно сильное влияние на число малых предприятий на 10 000 чел. населения в Краснодарском крае оказывает фактор Х₃ – уровень занятости в регионе. Фактор Х₁ – валовой региональный продукт на душу населения практически не влияет на исследуемый показатель.

На рисунке 3 приведен график построенного уравнения вместе в данными исследуемого показателя Y.

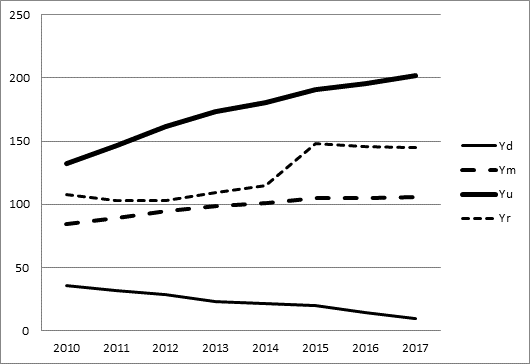
Рисунок 3.График нечеткой линейной регрессии для показателя числа малых предприятий на 10 000 человек населения в Краснодарского края, h = 0,5

Построенный график отражает достаточно устойчивую тенденцию числа

малых предприятий на 10 000 человек населения в Краснодарском крае, принимающего начиная с 2015 года среднее значение между его модальными значениями и оптимистическим прогнозом исследуемого показателя. Необходимо отметить, что с 2014 года реальные значения числа малых предприятий в регионе все больше удаляются от пессимистического прогноза. Для выяснения причин этой ситуации необходимы дополнительные исследования.

В результате проведенного анализа можно предложить следующий алгоритм анализа и прогнозирования экономических показателей с использованием метода нечеткой линейной регрессии:

1. Ввод данных для анализа экономических показателей за исследуемый период.

2. По каждому из исследуемых регионов решается соответствующая задача линейного программирования (6) с использованием программных средств.

3. Анализ построенного уравнения нечеткой регрессии с выбранным порогом надежности с целью выявления факторов, оказывающих большее влияние на исследуемый показатель.

4. Оценка результатов исследования с помощью контролирующей выборки для построенной модели.

5. Разработка рекомендаций для улучшения деятельности исследуемого процесса.

Предложенный в работе метод целесообразно использовать для анализа и прогнозирования значений различных экономических показателей. Созданная программа на языке Python позволяет анализировать показатели различных отраслей с визуальным представлением данных не только региональной экономики.