Система оценки технологического предпринимательства на основе нейронной сети и математического моделирования

Введение

В современном мире один из основных ключей к развитию и лидерству принадлежит сфере технологий. Мировые технологические державы, такие как Япония, Китай, США, Швейцария, разрабатывают инновационные продукты, открывают новые рынки, что способствует развитию их экономики, подъему уровня экономических показателей.

Российские разработки также являются востребованными на рынке, но для того чтобы стоять на одном уровне с мировыми лидерами или опережать в определенных направлениях, необходимо поднимать уровень технологического предпринимательства, являющийся важной составной частью инвестиционного климата.

Агентством стратегических инициатив был разработан эффективный инструмент оценивания инвестиционной привлекательности регионов России – национальный рейтинг состояния инвестиционного климата [16]. Также данный инструмент является продуктивным с точки зрения мотивации, так как органам власти каждого региона важно поднимать рейтинг ежегодно, стремясь к достижению более высоких показателей в сравнении с предыдущими результатами. Повышению рейтинга региона может способствовать влияние на развитие технологического предпринимательства, которое также нуждается в оценке. В таком случае возникает потребность в разработке критериев, на основании которых должна происходить оценка, и непосредственно механизме оценивания, учитывающем быстроизменяющуюся ситуацию и, как следствие, изменяющиеся значения критериев. Такой гибкостью обладают нейронные сети и математическое моделирование на основе алгоритмов.

Цель исследования заключается в разработке системы оценки уровня состояния технологического предпринимательства регионов на основе принципов нечеткой логики с использованием математического моделирования.

Научная новизна состоит в исследовании ключевых критериев оценки технологического предпринимательства и расчета их взаимозависимости и влияния на итоговую оценку, а также применении раннее не используемого в данном направлении инструмента – алгоритма Мамдани.

Авторская гипотеза заключается в том, что для оценки состояния любой сферы, для которой характерны быстрые изменения (рост, спад показателей), необходимо применять автоматизированные системы расчета оценки, способные быстро реагировать на данные изменения.

Для достижения поставленной цели были применены методы анализа и моделирования.

Разработка нейронной сети

Дальний Восток России на протяжении последних лет является динамично развивающейся частью Российской Федерации, столица макрорегиона – Приморский край, являющийся регионом повышенной значимости с точки зрения развития взаимодействия Российской Федерации со странами АТР, разработка и реализация совместных инновационных проектов позволит повысит уровень технологического предпринимательства как региона, так и страны в целом.

Оценивая важность развития технологического предпринимательства, в первую очередь необходимо выявить критерии, на основании которых можно оценить уровень развития данного сегмента экономической деятельности. Так как сфера технологического предпринимательства является достаточно обширной и многогранной, критерии оценки должны учитывать этот фактор. То есть второй задачей при разработке данной системы оценивания является переход к ее автоматизированности. Систематизировать набор критериев, сгруппировать их, определив общие группы, и преобразовать унифицированную модель способны нейронный сети [22] (Trofimova, 2017).

Первым этапом при разработки нейронной сети является выявление необходимых критериев (нейронов), на основании которых будет производиться прогноз развития определенных направлений.

При рассмотрении технологического предпринимательства сквозь призму реализуемых на территории Приморского края дорожных карт, нацеленных на поднятие рейтинга инвестиционного климата, можно выделить два ключевых направления, влияющих на состояние технологического предпринимательства – «Инвестиции» и «Предпринимательство» [2].

Инвестиции являются неотъемлемой частью рассматриваемого типа предпринимательства. Вкладываемый в новые технологии, разработки капитал ускоряет процесс получения готового продукта и выхода его на рынок. Предпринимательство является одним из источников инновационных технологий и непосредственным исполнителем идей.

Для построения нейронной сети с целью демонстрации прогноза развития выбранных направлений будет достаточно трех критериев. Это обусловлено тем, что при данном количестве нейронов программа, в которой будет построена сеть, позволит максимально быстро, точно и без сбоев в работе отобразить получившийся результат программирования [9] (Іzmұkhanov, 2020).

Критерии оценки состояния технологического предпринимательства в Приморском крае следующие:

1. Число предпринимательских организаций, выполняющих научные исследования и разработки, – данный критерий включает в себя развитие и повышение уровня научно-исследовательских разработок в уже существующих компаниях, а также открытие новых предпринимательских организаций; единицы измерения – шт.

Представленный критерий обусловлен отсутствием в предпринимательском секторе организаций, ориентированных и развивающий научные исследования и разработки на основе проведенного анализа (данные подтверждены статистической информацией территориального органа Федеральной службы государственной статистики по Приморскому краю [1] (Baygulov, 2020)).

2. Информирование граждан о взаимодействии с инвесторами – данный критерий включает в себя наполнение Инвестиционного портала ПК информацией об инвесторах, воспользовавшихся мерами господдержки, а также продвижение сайта; измерение производится по 5-балльной шкале, стандартизированному инструменту измерения достижения цели, применяемому в широком спектре сфер.

3. Инвестирование в научно-технологический сектор – критерий предполагает вложение капитала со стороны государства и инвесторов в научно-технологические разработки университетов, проектных команд, бизнеса, производственных предприятий; измерение критерия в млн рублей.

Следующий этап – определение веса каждого критерия [8] (Golovko, 2017). В рамках развития технологического предпринимательства в регионе с учетом тех условий, которые уже заданы (уровень развития инвестиционного климата Приморского края в целом), наиболее приоритетным критерием является информирование граждан о взаимодействии с инвесторами, вес критерия – 0,9. Второй по важности критерий – инвестирование в научно-технологический сектор, вес критерия – 0,6. Третий в иерархии показатель – число предпринимательских организаций в секторе научно-исследовательских разработок, вес – 0,4. Определенные в данном разделе критерии с учетом их весов являются одной из основ для разработки нейронной сети. В таблице 1 приведены данные, описанные выше.

Таблица 1

Переменные нейронной сети

Источник: составлено авторами по: стат. данным территориального органа Федеральной службы государственной статистики по Приморскому краю [21].

Визуализация данных продемонстрирована на графиках ниже (рис. 1). Для равной оценки состояния каждого критерия введена единая балльная шкала от 0 до 5, где высокое значение приравнено к оценке «5», среднее – к оценке «3», низкое – к оценке «2».

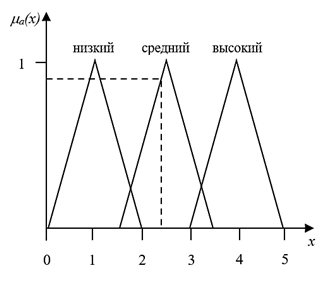
Рисунок 1. Присвоение переменной y₁ функции принадлежности

Источник: составлено авторами.

На рисунке пунктирной линий отображен уровень переменной y₁, на котором находится Приморский край на данный момент, то есть информирование граждан о взаимодействии с инвесторами происходит на среднем уровне.

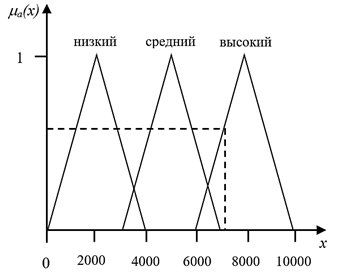
Рисунок 2. Присвоение переменной y₂ функции принадлежности

Источник: составлено авторами.

График (рис. 2) показывает, что на данный момент объем инвестиций в научно-технологический сектор составляет 7 млн руб.

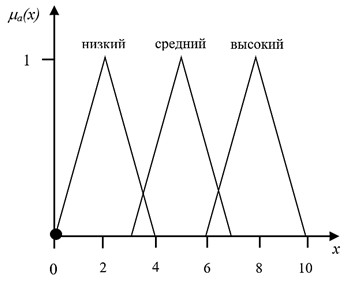
Рисунок 3. Присвоение переменной y₃ функции принадлежности

Источник: составлено авторами.

График (рис. 3) демонстрирует отсутствие организаций в предпринимательском секторе в Приморском крае в настоящий момент времени, деятельность которых включает научные исследования и разработки.

Третий этап – непосредственно построение нейронной сети для оценки технологического предпринимательства в Приморском крае на основе полученных результатов подготовительных этапов (рис. 4), где:

- y_1, y_2, y₃ – переменные;

- H (high) – высокое значение;

- A (average) – среднее значение;

- L (low) – низкое значение;

- M (mathematical formalization) – математическая формализация;

- j – весовой коэффициент.

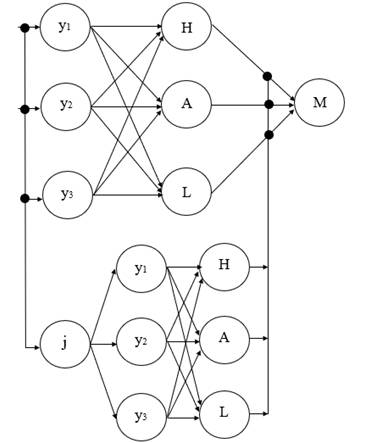
Рисунок 4. Нейронная сеть для оценки технологического предпринимательства в Приморском крае

Источник: составлено авторами.

Математическая формализация представленной нейронной сети [23] (Tsurikov, 2019):

(1)

Анализируя результат расчетов по формуле 1, можно утверждать о среднем уровне развития технологического предпринимательства в Приморском крае. При этом, если рассматривать каждый показатель (переменную) индивидуально на основании графиков (рис. 1–3), а также расчета по формуле, можно отметить, что первый критерий находится на среднем уровне, то есть необходимо прорабатывать направление по информированию граждан о возможности взаимодействия с инвесторами. Второй критерий находится на высоком уровне, что свидетельствует о крупных финансовых вложениях в НИОКР. Третий критерий находится на нулевой отметке графика и в формуле приравнивается к 0, то есть данный показатель требует особого внимания со стороны органов власти.

Применение теории нечетких множеств и нечеткой логики

При моделировании широкого класса реальных объектов возникает необходимость принимать решения в условиях неполной нечеткой информации. Современным перспективным направлением моделирования различного вида неопределенностей является теория нечетких множеств. В рамках теории нечетких множеств разработаны методы формализации и моделирования рассуждений человека, таких понятий, как «более или менее высокий уровень инфляции», «устойчивое положение на рынке», «более ценный» и т.д. [11] (Konysheva, Nazarov, 2015).

Необходимость на практике постоянно принимать решения в условиях неполной и нечеткой информации показывает, что теория нечетких множеств является стратегическим инструментом управления сложными системами [18] (Chyornyy, Vasilchenko, Gudim, Poley, Buzikaeva, 2018). Технологии и алгоритмы, разработанные в рамках этой теории, являются универсальными по применимости.

Впервые термин «нечеткие множества» (Fuzzy Sets) предложил американский ученый Л. Заде в 1965 г. [3] (Golosovskiy, Bogomolov, Terebov, Evtushenko, 2018). Именно его идеи дали толчок для развития «нечеткой математики», включающей в себя наряду с аппаратом нечетких множеств и другие приемы работы с неопределенностью [14] (Maksimova, Chernyy, Sukhorukov, 2021).

Основная идея Л. Заде состоит в расширении классического канторовского понятия множества. Если функция принадлежности «обычного множества» может принимать только два значения – 0 или 1, то в случае нечеткого (fussy) множества ее значения заполняют весь отрезок [0, 1] [24] (Chernyy, Vasilchenko, Gudim, Poley, Buzikaeva, 2018). Л. Заде ввел понятие лингвистической переменной, которая может принимать как числовое значение, так и лингвистическое.

Л. Заде также обратил внимание на тот факт, что словесной оценке переменной можно поставить в соответствие функцию, принимающую значения на отрезке [0, 1], т.е. функцию принадлежности некоторому нечеткому множеству [6, 13] (Luneva, 2018). Словесную оценку лингвистической переменной можно рассматривать как выражение x is l, где x – переменная, l – словесное (лингвистическое) значение, являющееся неформальной оценкой количества или интенсивности.

Для нечетких множителей вводится понятие нечетко лингвистических переменных. Нечеткая переменная описывается набором (α, χ, A), где α – название переменной, χ – универсальное множество (область α), A – нечеткие множества на x, описывающие ограничение (MA(x) на значение нечеткой переменной α) [7] (Gafarov, Galimyanov, 2017).

Значением нечетной лингвистической переменной могут быть нечеткие переменные, описывается набором (В, Т, X, G, P), B – лингвистическое, T – множества ее значений, представляющих собой наименование нечетких переменных – X, областью определения каждой из которых является множество – X. Множество T называется базовой лингвистической переменной [17] (Burakov, 2016). G – синтаксическая процедура, позволяющая оперировать элементами – T (например, генерировать новые значения), M – синтаксическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образующая процедурой G в нечеткого переменного, т.е. сформировать соответствующие нечеткие множество.

Возвращаясь к оценке технологического предпринимательства, необходимо отметить, что в сфере нечетких множеств наиболее подходящими для описания процессов и составления прогнозов, имеющих специфические особенности, неточные, изменяющиеся данные, риски являются алгоритмами нечеткого вывода.

Основными этапами нечеткого вывода являются [4] (Antipin, 2016):

1. Формирование базы правил (нечеткая база знаний).

2. Фаззификация (установка соответствия между

функцией принадлежности и входной переменной

на прямоугольной системе координат).

3. Процесс активизации (сопоставление лингвистических переменных).

4. Аккумуляция (процедура объединения).

5. Дефаззификация (процесс перехода от нечеткости

к числовому значению).

Порядок действий в системе нечеткого логического вывода отображен на рисунке 5.

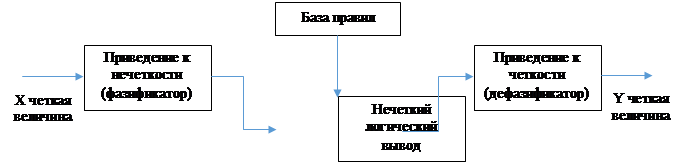
Рисунок 5. Система нечеткого логического вывода

Источник: составлено авторами.

Для моделирования прописанных выше составляющих нейронной сети будет использован математический аппарат, визуализированный на рисунке 9. Нейронная сеть будет функционировать следующим образом.

Слой 1. Фаззификация – проведение соответствия между переменными и функцией принадлежности, используя прямоугольную систему координат, где по вертикальной оси установлен уровень соответствия от 0 до 1 (0 – соответствие отсутствует, 1 – полное соответствие), а по горизонтальной – единицы измерения оцениваемого критерия. В качестве переменной будет выступать «у».

Слой 2. Формирование базы правил (нечеткой базы знаний). Создание такой базы происходит с помощью алгоритмов, например, Мамданы, Сугено [10, 12] (Kazantseva, 2017; Kopyrina, 2017). В таблице 2 база знаний построена по принципу алгоритма Мамдани.

Таблица 2

Нечеткая база знаний переменной у

Слой 3. Активизация – соотнесение лингвистических переменных путем определения степени истинности входных и выходных переменных. Например, y₁ – высокое значение, y₂ – среднее значение, y₃ – среднее значение, тогда результатом активизации будет среднее значение показателя.

В данном случае при оценке технологического предпринимательства 2 и 3 слой объединены в один, так как использование вспомогательных переменных не требуется, таким образом, выстроив базу правил, можно сразу определить значение конечного показателя в интересующих заданных условиях.

Слой 4. Дефаззификация – переход от лингвистических переменных к числовым значениям. Является заключительным этапом в построении нейронной сети на основе нечеткой логики, на данной шаге происходит преобразование полученных лингвистических переменных в числовые значения для оценки уровня технологического предпринимательства. Например, показатель имеет шкалу оценивания от 0 до 5, где 2 – низкое значение, 3 – среднее, 5 – высокое. Тогда в случае, если показатель на этапе активизации получил лингвистическую оценку «среднее», значит, в соотношении с числовым значением критерий можно оценить в 3 балла.

Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефаззификации.

Первую систему управления, основанную на нечетких множествах и лингвистических переменных, предложил английский математик Ибрагим Мамдани в 1975 г. в качестве системы управления паровым двигателем [15].

Алгоритм Мамдани описывает процессы, выполняемые последовательно, где каждый последующий этап получает на входе результат (выход) предыдущего [19] (Postnikov, Ryasnova, 2017). То есть работа данного алгоритма построена на принципе «черного ящика». На промежуточных этапах используется аппарат нечеткой логики и теория нечетких множеств. Особенность использования нечетких систем заключается в возможности управления обычными числовыми данными, при этом используя гибкие возможности, предоставляемые системами нечеткого вывода. Отличительная особенность данного типа алгоритма выявлена на первоначальном этапе разработки, а именно на этапе формирования базы правил, где числовые переменные, устанавливаемые для анализа, задаются в виде отрезка чисел. Данный алгоритм применяется в тех ситуациях, когда, к примеру, необходимо произвести прогноз на будущие периоды, при таких условиях невозможно судить с точностью до конкретных числовых показателей о развитии определенных направлений.

Формализованно описанный алгоритм нечеткого вывода имеет следующий вид (формулы 2–7 [20] (Solovev, Kuzora, 2019)):

1. (x₁ = a_{неч 1j} q_x2 = a_{неч 2j} q…q _xn = a_{неч nj} с весом w_j) Þ y=d_{неч j}, j=1,m, (2)

где a_{неч nj} – нечеткий терм входной переменной, оцениваемый значениями x_n ; q – логическая операция; Þ – символ активизации; d_{неч j} – нечеткий терм выходной переменной, оцениваемый у; m – номер правила в базе знаний;

2. b_i = µ_an(x), (3)

где b_i – лингвистическая переменная; µ_an(x) – функция принадлежности терма входной переменной;

3. µ_an(x) = µ_dn(y), → c_i = µ_d (y), (4)

где → – знак следствия; c_i – лингвистическая переменная; µ_dn(y) – функция принадлежности терма выходной переменной;

4. µ_с (у) = max { c₁, c₂, …, c_n}, (5)

где µ_с (у) – результат объединения.

5. , (6)

или

, (7)

где у₁ – результат дефаззификации методом центра тяжести; у₂ – результат дефаззфикации методом центра площади.

Другим подходом к построению алгоритма нечеткого вывода, получившего широкое распространение, как и алгоритм Мамдани, является работа Т. Такаги и М. Сугено. Его ключевой отличительной от алгоритма Мамдани чертой является установление переменных в базе правил в виде конкретные чисел, а не отрезков, как в предыдущем примере. То есть не требуется аккумуляция значений, так как получены дискретные множества точных значений для каждой выходной лингвистической переменной.

Алгоритм Сугено формализованно выглядит следующим образом (формулы 8–9 [20] (Solovev, Kuzora, 2019)):

1. (x₁ = a_{неч 1j} q_x2 = a_{неч 2j} q…q _xn = a_{неч nj} с весом w_j) Þ y = b_j1+ b_j2+…+ b_jn, j=1,m, (8)

где b_jn – действительные числа.

2. идентичен алгоритму Мамдани.

3. µ_an(x) – действительное число.

4. этап аккумуляции отсутствует.

5. (9)

где у – результат дефаззификации методом центра тяжести для одноточечных множеств.

Преимущества алгоритма Сугено заключаются в меньшей трудоемкости проведения расчетов на его основе, а также в способности моделировать очень сложные системы, адекватное описание которых с помощью схемы Мамдани практически невозможно из-за крайне большого числа формирующихся взаимосвязей между нечеткими параметрами. К слабым сторонам алгоритма Сугено можно отнести то, что он не позволяет представлять выходные переменные в лингвистической форме, а настройка параметров функций принадлежности представляет собой сложную задачу нелинейного программирования, для решения которой, однако, существуют эффективные методы, например опирающиеся на аппарат искусственных нейронных сетей [10] (Kazantseva, 2017).

Основываясь на вышеперечисленных характеристиках алгоритмов, можно сделать вывод о том, что наиболее приемлемым для оценки уровня развития технологического предпринимательства в Приморском крае является алгоритм Мамдани в силу его расширенного спектра возможных событий. Для построения данного алгоритма необходимо воспользоваться программой MathLab с пакетом расширения Fuzzy Logic Toolbox [5] (Bobyr, 2016), первоначально определив количество критериев, на основании которых будет производиться оценка, а также наделив каждый критерий весом. Затем создать базу правил и далее производить расчеты и построение графиков в программе.

Алгоритм Мамдани для оценки технологического предпринимательства в Приморском крае

Оценка уровня развития технологического предпринимательства в Приморском крае включает два основных этапа:

1. Введение входных переменных на основе выделенных критериев.

2. Результат оценки 1-го этапа.

Для начала работы необходимо в командной строке ввести команду fuzzy. Следующая работа представлена в виде упорядоченных шагов.

1) для лаконичного представления в схеме критериев оценки необходимо сократить их наименования:

- «информирование граждан о взаимодействии с инвесторами» – «инвестор»;

- «число предпринимательских организаций, выполняющих научные исследования и разработки» – «исслед.орг-ции»;

- «инвестирование в научно-технологический сектор» – «инвестиции».

Для определения лингвистических переменных требуется добавить входные переменные «инвестор», «исслед.орг-ции», «инвестиции» с помощью функции Add input в меню Edit, а также изменить имя выходной переменной на «оценка». В итоге получается следующая структура: три входа, алгоритм нечеткого вывода Мамдани (средний блок), один выход (рис. 6).

Рисунок 6. Ввод лингвистических переменных

Источник: составлено авторами.

2) для каждой входной и выходной переменных необходимо присвоить функции переменных в редакторе. Для переменной «инвестор» диапазон составляет от 0 до 5 баллов (рис. 7). Далее определяем тип trimf для трех функций принадлежности и присваиваем каждой последовательно наименования: низкая, средняя, высокая (оценка). Для переменной «инвестиции» диапазон составляет от 0 до 10 000 млн руб. Функция принадлежности определяется схоже с функцией принадлежности «инвестор». Третья переменная задана в диапазоне от 0 до 10 единиц. Функция принадлежности определяется аналогично предыдущим. Для выходной переменной «оценка» диапазон действует от 0 до 5, функция принадлежности идентичная входным переменным.

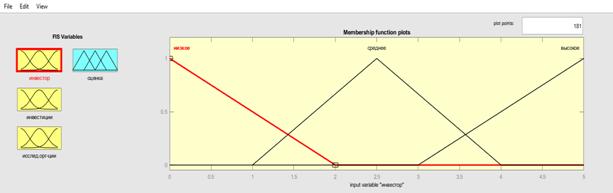
Рисунок 7. Присвоение переменным функций принадлежности

Источник: составлено авторами.

3) завершающим шагом в процессе построения математической модели оценки технологического предпринимательства является создание базы знаний (базы правил), задающей взаимосвязь входных и выходных переменных. Написать базу возможно в редакторе правил (rule editor), комбинируя между собой три варианта оценок (низкая, средняя, высокая) трех переменных. То есть в результате получается 27 правил. Фрагмент базы представлен на рисунке 8.

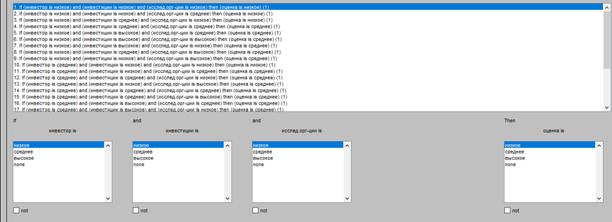
Рисунок 8. Фрагмент созданной базы правил

Источник: составлено авторами.

4) далее функцией View открывается окно Rule Viewer, демонстрирующее зависимость вышеописанных этапов. В окне input либо передвижением красных управляющих линий каждой группы трех переменных задаем исходные значения, получаем в результате оценки технологического предпринимательства Приморского края: «инвестор» – 2,52, «инвестиции» – 7040, «исслед.орг-ции» – 0. По итогу получаем оценку, равную 2.5 (рис. 9). Расчет итоговой оценки производится следующим образом:

А. Соотнести значения переменных с оценкой функций («инвестор» со значением 2,52 = 3, «инвестиции» со значением 7040 = 5, «исслед.орг-ции» со значением 0 = 0).

Б. Найти среднее арифметическое значение между переменными: ((3+5+0)/3) = 2,6, что практически равно полученному значению в программе (пакет Fuzzy Logic Toolbox допускает погрешность).

Таким образом, на данном этапе происходит замена лингвистических переменных на числовые (дефаззификация).

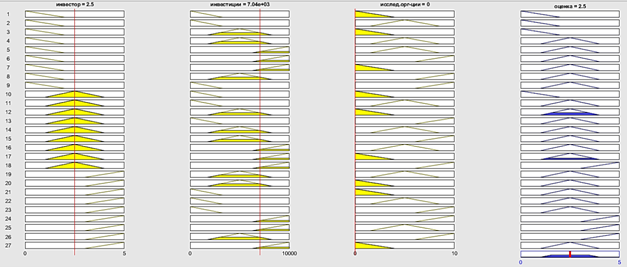
Рисунок 9. Графический результат оценки

Источник: составлено авторами.

5) последний этап – выведение трехмерной модели, демонстрирующей результат оценки двух входных переменных (рис. 10). Редактор позволяет задавать любое сочетание двух входных переменных из трех, при этом ось z всегда будет выходной переменной. 3D-модель отражает значимость каждой переменной и влияние на итоговую оценку.

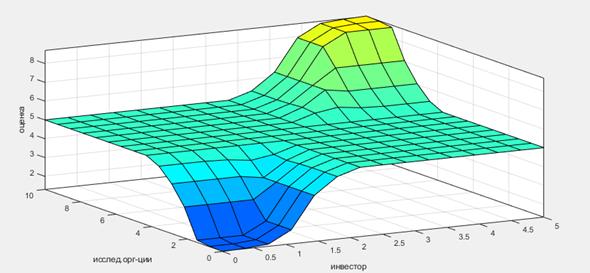
Рисунок 10. Трехмерная модель оценки технологического предпринимательства на основании двух входных переменных: «инвестор» и «исследовательские организации»

Источник: составлено авторами.

Реализовав все этапы создания алгоритма Мамдани, можно сделать вывод о том, что состояние технологического предпринимательства Приморского края соответствует оценке 2,5 баллов, основанной на предложенных в работе критериях. Данная оценка соответствует лингвистической переменной «средняя». Оценку подтверждает и формализованное представление нейронной сети (формула 1).

То есть для повышения оценки и, как следствие, улучшения инвестиционного климата Приморского края следует воздействовать на развитие трех предложенных критериев. В конечном итоге влияние на данные показатели будет способствовать повышению Приморского края в рейтинге инвестиционной привлекательности регионов АСИ.

Методика применения системы нечеткой логики и алгоритма Мамдани для оценки технологического предпринимательства

На основе вышеизложенного материала составлены методические указания применения системы нечеткой логики и алгоритма Мамдани для оценки технологического предпринимательства с целью передачи результата исследования и итоговой разработки Правительству Приморского края, а именно Агентству проектного управления, одним из направлений работы которого является мониторинг деятельности приморских предпринимателей, а именно: их развитие, взаимодействие с государством (органами власти) и инвесторами.

Для наиболее точной интерпретации и применения предлагаемой разработки необходимо указать этапы, которые нужно осуществить для получения достоверного результата.

Процесс оценки состояния технологического предпринимательства можно разделить на несколько основных этапов:

Этап 1. Выявление критериев – необходимо проанализировать объект оценки и факторы, влияющие на него. Из них выделить наиболее значимые (для комфортной работы с системой MathLab, а также минимизации степени погрешности стоит выбирать не более трех-четырех критериев). Далее определить вес каждого критерия.

Этап 2. Построение нейронной сети. Выделенным критериям определить лингвистические переменные (оценки от низкой до высокой), затем лингвистические переменные преобразовать в числовые.

На основе выявленных критериев и определенных весовых коэффициентов построить нейронную сеть, где критерии являются входными переменными, переведенными из лингвистической переменной в числовую. Выход – выходная переменная – оценка, полученная в итоге расчетов значений критериев и их весов. Оценка демонстрирует состояние развития технологического предпринимательства в регионе.

Этап 3. Алгоритм Мамдани. Построение алгоритма Мамдани начинается с создания базы знаний (базы правил) с использованием всех критериев (переменных) и их числового диапазона для низкой, средней и высокой оценок. На основании базы правил алгоритм Мамдани просчитывает результат в виде искомой оценки. При верных расчетах оценки нейронной сети и алгоритма должны совпадать (при этом необходимо учесть погрешность, с которой делает расчеты программа MathLab в случае, если применяется данный программный продукт для реализации 3 этапа представленной методики).

В представленной работе были определены на примере Приморского края – столицы Дальнего Востока и важного с точки зрения взаимодействия со странами АТР субъекта РФ – ключевые критерии для оценки технологического предпринимательства на основании взаимосвязи показателей национального рейтинга АСИ и показателей дорожных карт Приморского края. Такими критериями являются: число предпринимательских организаций, выполняющих научные исследования и разработки, информирование граждан о взаимодействии с инвесторами и инвестирование в научно-технологический сектор.

Показатели данных критериев могут часто изменяться – как расти, так и уменьшаться. В условиях часто меняющихся и неточных данных оценка текущего состояния определенной сферы и прогнозирование на будущий период наиболее эффективны при помощи нейронной сети, учитывающей выявленные критерии в качестве входных данных, преобразующей лингвистические переменные в числовые в целях единого, унифицированного расчета и получения максимально достоверной итоговой оценки.

В работе разработана такая полносвязная нейронная сеть для оценки состояния технологического предпринимательства, учитывающая вес каждого критерия при выведении результата. Итоговая оценка, согласно данной методике, равна 2,6, что можно интерпретировать как среднюю оценку.

Для подтверждения полученного результата и визуализации процесса оценки, а также гибкого, быстрого реагирования на любые изменения, корректировки значений входных переменных (критериев) в работе использован алгоритм Мамдани, описан каждый шаг его создания: ввод входных переменных, присвоение функций переменных для каждого критерия и определение диапазона действия, создание базы правил и их визуализация, а также использование трехмерной модели предложенной оценки.

В конечном итоге оценка развития технологического предпринимательства в Приморском крае на основании алгоритма Мамдани составила 2,5 балла, что также соответствует средней оценке и практически равно оценке нейронной сети (пакет расширения Fuzzy Logic Toolbox, используемый в программе MathLab, дает погрешность в расчетах, что является его недостатком).

Заключение

Таким образом, выбранный инструмент для оценки технологического предпринимательства является эффективным средством при использовании неточных данных, а также при прогнозировании будущей ситуации. Полученная оценка в результате применения двух дополняющих друг друга методов и создающих полноценную базу свидетельствует о том, что наиболее актуальным является воздействие на число организаций, реализующих научные исследования и разработки, затем необходимо повысить уровень информирования граждан и возможности взаимодействия с инвестором, а также непосредственно увеличивать уровень потока инвестиций. Согласно проведенным исследованиям, сосредоточение внимания на повышении показателей данных критериев поспособствует улучшению уровня развития технологического предпринимательства Приморского края.

В результате разработаны методические указания применения системы нечеткой логики и алгоритма Мамдани для оценки состояния технологического предпринимательства.