Учет критериев риска при принятии управленческих решений

Элементы неопределенности, присущие функционированию и развитию многих экономических процессов, обуславливают появление ситуаций, не имеющих однозначного исхода (решения). Это обстоятельство усложняет процесс принятия решений в условиях неопределенности и предопределяет необходимость использования соответствующих методов, которые дают возможность по заданным целям и ограничениям получить приемлемые для практики (оптимальные или рациональные) управленческие решения.

Как известно, в зависимости от степени неопределенности различают ситуации риска и ситуации неопределенности. При этом ситуация риска, являясь разновидностью неопределенной ситуации, характеризуется тем, что в результате каждого действия могут быть получены различные результаты, вероятность которых известна или может быть оценена.

На методы принятия решений в условиях риска существенным образом накладывают отпечаток многообразия критериев и показателей, посредством которых оценивается уровень риска. Принятие решений в условиях риска может быть основано на одном из следующих критериев:

‑ критерий ожидаемого значения;

‑ комбинации ожидаемого значения и дисперсии;

‑ известного предельного уровня;

‑ наиболее вероятного события в будущем.

Рассмотрим более подробно применение этих критериев.

Критерий ожидаемого значения (КОЗ). Использование КОЗ предполагает принятие решения, обуславливающего максимальную прибыль при имеющихся исходных данных о вероятности полученного результата при том или другом решении. По существу, КОЗ представляет собой выборочные средние значения случайной величины. Естественно, что достоверность получаемого решения при этом будет зависеть от объема выборки.

Так, если обозначить КОЗ - Е(x₁,x₂,...,x_n), где

x₁,x₂,...,x_n ‑ принимаемые решения при их количестве, равном n, то

E(x_i) ( ρ) M(x_i),

где M(x_i) ‑ математическое ожидание критерия.

Таким образом, КОЗ может применяться, когда однотипные решения в сходных ситуациях приходится принимать большое число раз.

Критерий «ожидаемого значения – дисперсия». КОЗ имеет область применения, ограниченную значительным числом однотипных решений, принимаемых в аналогичных ситуациях. Этот недостаток можно устранить, если применять комбинацию КОЗ и выборочной дисперсии s². Возможным критерием при этом является минимум выражения

E(Z, σ ) = E(Z) ± k·U(z),

где

E(Z, σ ) ‑ критерий «ожидаемого значения – дисперсия»;

k ‑ постоянный коэффициент;

U(Z) = m_Z/S ‑ выборочный коэффициент вариации;

m_Z ‑ оценка математического ожидания;

S - оценка среднего квадратического ожидания.

Знак «минус» ставится в случае оценки прибыли, знак «плюс» - в случае затрат.

Из приведенной зависимости видно, что в данном случае точность предсказания результата повышается за счет учета возможного разброса значений E(Z), то есть введения своеобразной «страховки». При этом степень учета этой страховки регулируется коэффициентом k, который как бы управляет степенью учета возможных отклонений. Так, например, если для ЛПР имеет большое значение ожидаемые потери прибыли, то k>>1 и при этом существенно увеличивается роль отклонений от ожидаемого значения прибыли E(Z) за счет дисперсии.

Критерий предельного уровня. Этот критерий не имеет четко выраженной математической формулировки и основан в значительной степени на интуиции и опыте ЛПР. При этом ЛПР на основании субъективных соображений определяет наиболее приемлемый способ действий. Критерий предельного уровня обычно не используется, когда нет полного представления о множестве возможных альтернатив. Учет ситуации риска при этом может производиться за счет введения законов распределений случайных факторов для известных альтернатив. Несмотря на отсутствие формализации, критерием предельного уровня пользуются довольно часто, задаваясь значениями случайных факторов на основании экспертных или опытных данных.

Критерий наиболее вероятного исхода. Этот критерий предполагает замену случайной ситуации детерминированной путем замены случайной величины прибыли (или затрат) единственным значением, имеющим наибольшую вероятность реализации. Использование данного критерия, также как и в предыдущем случае в значительной степени опирается на опыт и интуицию. При этом необходимо учитывать два обстоятельства, затрудняющие применение этого критерия:

‑ критерий нельзя использовать, если наибольшая вероятность события недопустимо мала;

‑ применение критерия невозможно, если несколько значений вероятностей возможного исхода равны между собой.

Неопределенные пассивные условия. Неопределенные факторы, закон распределения которых неизвестен, являются наиболее характерными при исследовании качества адаптивных систем. Именно на этот случай следует ориентироваться при выборе гибких конструкторских решений. Методический учет таких факторов базируется на формировании специальных критериев, на основе которых принимаются решения. Критерии Вальда, Сэвиджа, Гурвица и Лапласа уже давно и прочно вошли в теорию принятия решений.

В соответствии с критерием Вальда в качестве оптимальной выбирается стратегия, гарантирующая выигрыш не меньший, чем «нижняя цена игры с природой»:

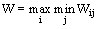
Правило выбора решения в соответствии с критерием Вальда можно интерпретировать следующим образом: матрица решений [W_ir] дополняется еще одним столбцом из наименьших результатов W_ir каждой строки. Выбрать надлежит тот вариант, в строке которого стоит наибольшее значение W_ir этого столбца.

Выбранное таким образом решение полностью исключает риск. Это означает, что принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Какие бы условия V_j не встретились, соответствующий результат не может оказаться ниже W. Это свойство заставляет считать критерий Вальда одним из фундаментальных. Поэтому в технических задачах он применяется чаще всего как сознательно, так и неосознанно. Однако в практических ситуациях излишний пессимизм этого критерия может оказаться очень невыгодным.

Применение этого критерия может быть оправдано, если ситуация, в которой принимается решение, характеризуется следующими обстоятельствами:

‑ о вероятности появления состояния V_j ничего не известно;

‑ с появлением состояния V_j необходимо считаться;

‑ реализуется лишь малое количество решений;

‑ не допускается никакой риск.

Критерий Байеса-Лапласа в отличие от критерия Вальда, учитывает каждое из возможных следствий всех вариантов решений:

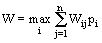
Соответствующее правило выбора можно интерпретировать следующим образом: матрица решений [W_ij] дополняется еще одним столбцом, содержащим математическое ожидание значений каждой из строк. Выбирается тот вариант, в строках которого стоит наибольшее значение W_ir этого столбца.

Критерий Байеса-Лапласа предъявляет к ситуации, в которой принимается решение, следующие требования:

‑ вероятность появления состояния V_j известна и не зависит от времени;

‑ принятое решение теоретически допускает бесконечно большое количество реализаций;

‑ допускается некоторый риск при малых числах реализаций.

В соответствии с критерием Сэвиджа в качестве оптимальной выбирается такая стратегия, при которой величина риска принимает наименьшее значение в самой неблагополучной ситуации:

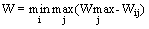
Здесь величину W можно трактовать как максимальный дополнительный выигрыш, который достигается, если в состоянии V_j вместо варианта U_i выбрать другой, оптимальный для этого внешнего состояния, вариант.

Соответствующее критерию Сэвиджа правило выбора следующее: каждый элемент матрицы решений [W_ij] вычитается из наибольшего результата max W_ij соответствующего столбца. Разности образуют матрицу остатков. Эта матрица пополняется столбцом наибольших разностей W_ir. Выбирается тот вариант, в строке которого стоит наименьшее значение.

Согласно критерию Гурвица выбирается такая стратегия, которая занимает некоторое промежуточное положение между крайним пессимизмом и оптимизмом:

где

ρ - коэффициент пессимизма, выбираемый в интервале [0,1].

Правило выбора согласно этому критерию следующее: матрица решений [W_ij] дополняется столбцом, содержащим средние взвешенные наименьшего и наибольшего результатов для каждой строки. Выбирается тот вариант, в строках которого стоят наибольшие элементы W_ir этого столбца.

При ρ =1 критерий Гурвица превращается в критерий Вальда (пессимиста), а при ρ =0 - в критерий азартного игрока. Отсюда ясно, какое значение имеет весовой множитель ρ . В технических приложениях правильно выбрать этот множитель бывает так же трудно, как правильно выбрать критерий. Поэтому чаще всего весовой множитель ρ =0.5 принимается в качестве средней точки зрения.

Критерий Гурвица предъявляет к ситуации, в которой принимается решение, следующие требования:

‑ о вероятности появления состояния V_j ничего не известно;

‑ с появлением состояния V_j необходимо считаться;

‑ реализуется лишь малое количество решений;

‑ допускается некоторый риск.

Критерий Ходжа-Лемана базируется одновременно на критериях Вальда и Байеса-Лапласа:

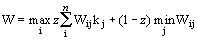
Правило выбора, соответствующее этому критерию, формулируется следующим образом: матрица решений [W_ij] дополняется столбцом, составленным из средних взвешенных (с постоянными весами) математического ожидания и наименьшего результата каждой строки. Отбирается тот вариант решения, в строке которого стоит наибольшее значение этого столбца.

При z=1 критерий преобразуется в критерий Байеса-Лапласа, а при z=0 превращается в критерий Вальда. Таким образом, выбор параметра z подвержен влиянию субъективизма. Кроме того, без внимания остается и число реализаций. Поэтому этот критерий редко применяется при принятии технических решений.

Критерий Ходжа-Лемана предъявляет к ситуации, в которой принимается решение, следующие требования:

‑ о вероятности появления состояния V_j ничего не известно, но некоторые предположения о распределении вероятностей возможны;

‑ принятое решение теоретически допускает бесконечно большое количество реализаций; допускается некоторый риск при малых числах реализаций.

Общие рекомендации по выбору того или иного критерия дать затруднительно. Однако отметим следующее: если в отдельных ситуациях недопустим даже минимальный риск, то следует применять критерий Вальда; если определенный риск вполне приемлем, то можно воспользоваться критерием Сэвиджа. Можно рекомендовать одновременно применять поочередно различные критерии. После этого среди нескольких вариантов, отобранных таким образом в качестве оптимальных, приходится волевым решением выделять некоторое окончательное решение.

Такой подход позволяет, во-первых, лучше проникнуть во все внутренние связи проблемы принятия решений и, во-вторых, ослабляет влияние субъективного фактора. Кроме того, в области технических задач различные критерии часто приводят к одному результату.

Следует отметить, что разработанные способы и приемы решения задач в условиях риска и неопределенности не ограничиваются перечисленными и рассмотренными выше методами. В зависимости от конкретной ситуации в процессе анализа используются и такие методы, как, среднеквадратическое отклонение и коэффициент вариации, способствующие решению задач, связанных с минимизацией риска.