Индекс эластичности потребительской ценности: новая модель потребительского выбора при ограниченном бюджете домохозяйства

Введение.

Современные исследования в области экономики потребления демонстрируют растущий интерес к задачам оптимизации потребительского выбора в условиях бюджетных ограничений. Анализ публикаций последних лет позволяет выявить три ключевых направления в моделировании зависимости спроса от цен: 1) применение методов математического программирования для максимизации полезности, 2) учет эластичности спроса по цене, 3) интеграцию поведенческих факторов в ценовые стратегии.

Работы российских экономистов в этой области предоставляют предпринимателям и маркетологам инструменты для балансировки между рыночной конъюнктурой и производственными затратами при формировании конечных цен.

Работы в этом направлении важны тем, что предоставляют предпринимателям инструмент для поддержания баланса между рыночной конъюнктурой и структурой затрат предприятий при формировании оптимальных цен.

Последние годы демонстрируют рост рационального потребления в России. Домохозяйства стремятся распределить свой бюджет так, чтобы получить наибольшую полезность от потребляемых товаров и услуг. Это приводит к склонности населения к более тщательному планированию своих трат и снижению числа импульсивных покупок в торговых точках, спровоцированных, например, различными промо-акциями и распродажами.

Так по мнению эксперта российской консалтинговой группы ИТ-компаний GlowByte, работающей на рынке внедрения аналитических решений для ритейла, Алексея Чванова и экспертов сетей «Лента», «О’кей» и платформы ценовой аналитики PriceTuner Тимофея Шульгина, Ольги Осиповой и Сергея Ипатова [1] российские покупатели становятся более зрелыми, ценят качество, ищут долгосрочную ценность и меньше подвержены импульсивным покупкам, вызванным скидками. Ритейлеры адаптируются, снижая промо-давление и ища новые способы удержания клиентов.

В эту "игру" включаются и банки, подыгрывая покупателям в их стремлении к оптимизации расходов, и выпуская разнообразные методички "8 простых правил оптимизации семейного бюджета" (Газпромбанк) [2].

Несмотря на обилие работ, ощущается недостаток исследований, комплексно рассматривающих задачу максимизации суммарной потребительской ценности при бюджетных ограничениях. В то время как инженеры располагают обширными справочниками опытным образом полученных величин, маркетологи часто полагаются на эмпирические маловоспроизводимые данные, что снижает точность прогнозов. Настоящая статья призвана восполнить этот пробел, предложив математическую модель для более точного прогнозирования спроса и оптимизации ценообразования. Авторы также делают попытку найти универсальный параметр для сравнения потребительской ценности различных товарных категорий.

Обзор литературы

Принцип предельной полезности

Принцип предельной полезности является фундаментальной концепцией в экономической теории, которая объясняет, как потребители принимают решения о распределении своего бюджета между различными товарами и услугами [3]. Этот принцип используется для анализа потребительского поведения, формирования цен и оптимизации рыночных стратегий.

Предельная полезность (MU) — это дополнительная полезность, которую получает потребитель от использования ещё одной единицы блага , которая уменьшается с ростом потребления (закон убывающей предельной полезности).

Для максимизации общей полезности при ограниченном бюджете потребители распределяют расходы так, чтобы предельная полезность на единицу затрат была одинаковой для всех товаров

Формула 1. Классическое условие максимизации общей полезности при ограниченном бюджете.

Где MU_i — предельная полезность товара i, а P_i — его цена.

Это условие в формуле Формула 1 выводится с помощью метода Лагранжа для задачи максимизации функции полезности , где — количество i-го товара при бюджетном ограничении , где — цена товара, I — доход.

Формула Формула 1 означает, что последний рубль, потраченный на каждый товар, приносит одинаковую полезность . Если бы это условие нарушалось (например, ), потребитель мог бы увеличить общую полезность, перераспределив расходы в пользу товара с более высоким отношением .

Разумеется, закон предельной полезности имеет и свои недостатки, так как люди могут переоценивать важность первых единиц товара и недооценивать снижение их ценности. В математическом смысле это выражается в том, что на самом деле MU не является константой, а зависит от x. А так как x зависит от P, то MU также зависит от P, что приводит к тому, что

Однако современные экономические исследования, в том числе в российской научной школе, все чаще указывают на ограничения линейных моделей спроса. Это связано с тем, что линейные функции не способны адекватно описывать насыщение рынка, психологические пороги потребления и нелинейное влияние дохода на структуру потребления.

Тем не менее, даже в таком линейном приближении принцип предельной полезности играет ключевую роль в экономическом анализе потребительского поведения и рыночного ценообразования. Он помогает понять, как люди принимают решения о покупках, и как компании могут оптимизировать свои ценовые стратегии для максимизации прибыли и удовлетворения спроса.

Функции затрат класса PIGLOG, модели AIDS и QUAIDS

Модель AIDS (Almost Ideal Demand System), предложенная Дитоном и Мюльбауэром (1980), является важным инструментом для анализа потребительского спроса [4].

Она основана на функции затрат класса PIGLOG и предполагает линейную связь между долей расходов на товар и логарифмом общих затрат.

Модель QUAIDS является расширением модели AIDS (Almost Ideal Demand System), разработанной Джеймсом Бэнксом, Ричардом Блунделлом и Артуром Левбелом в 1997 году [5]. Она включает квадратичные члены в уравнениях спроса, что позволяет лучше отражать нелинейные эффекты изменения цен и доходов на структуру потребления. Модель QUAIDS позволяет рассчитывать эластичности по доходу и цене, что важно для понимания реакции потребителей на изменения экономических условий.

Расширенный вариант этой модели использовался российскими экономистами Берендеевой Е.В. и Ратниковой Т.А. для моделирования реакции потребительского спроса российских домохозяйств на ввод различных продовольственных эмбарго в отношении РФ [6].

В работах российских эконометристов модель квадратичной почти идеальной системы спроса (QUAIDS) активно применяется и развивается. Как отмечают А. Г. Соломаха [26] и А. А. Бондарев [27], переход к квадратичным функциям спроса позволяет более точно отразить сложные эффекты дохода и цен, особенно при анализе потребительских корзин. С.А. Айвазян, Б.Е. Бродский и А.Н. Березняцкий [28] также подчеркивают, что нелинейные модели лучше улавливают структурные изменения в потребительском поведении, вызванные переходными процессами в экономике, а также инфляцией или кризисами.

Применение квадратичных зависимостей, как и в представленной в статье модели x=f(p), становится необходимым инструментом для подтверждения научной новизны и объяснения аномальных рыночных явлений.

Концепция «Кривой роста ценности»

Эта концепция, разработанная Арманом Касымом (2024), акцентирует внимание на первоначальной ценности продукта как на главном факторе спроса [7]. Она подчеркивает, что спрос определяется изначальной ценностью продукта, а также важностью внедрения только тех улучшений, которые реально усиливают ключевую ценность.

«Кривая роста ценности» предлагает свежий подход к управлению спросом, особенно актуальный для стартапов и компаний, работающих в условиях высокой конкуренции. В отличие от стратегии «голубого океана», эта концепция ориентирована на поддержание спроса в существующих конкурентных нишах.

Особенности потребительской ценности

Ценность товара зависит от многих качеств товара, среди которых большинство авторов выделяет следующие три: качество, цена и сервис. Повышение качества и уровня обслуживания способствует увеличению воспринимаемой ценности продукта. Уровень цены часто указывает потребителю на более качественный товар, что в общем случае не всегда является верным [8] [9].

При этом каждый покупатель имеет уникальные потребности и ресурсы, поэтому восприятие ценности одного и того же товара может значительно различаться между потребителями. Один может быть готов заплатить более высокую цену за высокое качество, в то время как другой может считать, что преимущества не оправдывают затрат.

Причем потребности и предпочтения покупателей со временем меняются, поэтому процесс формирования ценности должен быть непрерывным.

Ключевым отличием маркетингового подхода от чисто экономического является переход от абстрактного понятия «полезности» к прикладной категории «потребительской ценности» (Customer Value). Отечественные исследователи активно развивают концепцию ценности как основы конкурентной стратегии. Т.И. Товарищтай [29] рассматривает потребительскую ценность как ключевой фактор долгосрочного устойчивого развития компании, акцентируя внимание на необходимости ее объективного количественного измерения.

В этом контексте важнейшим инструментом анализа становится эластичность спроса по цене (EDP). Традиционные методы оценки EDP (например, по формуле дуговой или точечной эластичности) измеряют лишь реакцию спроса на изменение цены. Однако, как указывают Пальчикова Ю.В., Сазанова С.Л. [30], современный маркетинг требует интегральных показателей, которые учитывают не только цену, но и совокупность неценовых выгод, формирующих потребительскую ценность продукта.

Влияние бюджетных ограничений на потребительский выбор

Проблема бюджетных ограничений является центральной в российской экономической науке, особенно в периоды экономической нестабильности. Г.О. Хугаев [31] отмечает, что в условиях ограниченного дохода потребители переходят к более сложным стратегиям выбора, где предпочтения (функция полезности) модифицируются под влиянием текущего остатка бюджета.

Предложенная авторами настоящей статьи модель, интегрирующая потребительскую ценность и «бюджетный излишек», предоставляет аналитический аппарат для количественной оценки влияния его на спрос. Т.В. Киселева [32] подчеркивает, что именно такие модели, сочетающие теоретическую экономику с практическим маркетингом, имеют наибольшую практическую новизну, поскольку дают возможность компаниям прогнозировать и управлять поведением потребителей, чувствительных к цене, но при этом готовых платить больше за высокую воспринимаемую ценность.

Научная новизна и ценность подхода, используемая в настоящей работе

Авторы используют оптимизацию суммарной потребительской ценности (A) вместо классической функции полезности. Такой подход обеспечивает подтверждает научную ценность работы, поскольку:

1. Вводит метрику, основанную на ценности. В отличие от традиционных моделей, оперирующих долей расходов, используемый авторами данной публикации подход математически формализует индекс эластичности потребительской ценности (κ), который позволяет сравнивать ценностное восприятие разнородных товаров.

2. Объясняет аномалии через бюджетные ограничения. Введение порога потребления (X) и анализ свободного остатка бюджета (L>0) позволяет аналитически объяснить, почему спрос может расти при увеличении цены (т.е. объяснить неклассические реакции), что ранее было возможно только в рамках поведенческой экономики [33]. Например, рассматриваемый А.Ю. Сунякиной эффект ограниченной рациональности, наступающий тогда, когда человек при принятии решений сталкивается с проблемами (нехватка ресурса, времени и т. п.), в виду чего он не может быть полностью рационален [34].

Методология и методы

Постановка задачи

Авторы будут использовать несколько иные обозначения параметров, входящих в модель. Вместо понятия «полезность» U будет использоваться привычное для маркетологов понятие «потребительская ценность» A (от слова Avantage), вместо «предельная полезность» MU – «удельная потребительская ценность» a. Авторы являются маркетологами-аналитиками, и такая терминология более привычна для сферы маркетинга. Пусть читатели-экономисты не обессудят.

Классическая модель максимизации функции полезности, а в нашей терминологии функции потребительной ценности , при бюджетном ограничении образует ядро большинства современных исследований. В них целевой функцией является . Это в итоге приводит решению систем вида:

Формула 2. Простейшая модель максимизации функции полезности при бюджетном ограничении.

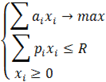
Эта система уравнений и условий учитывает все необходимые параметры, которые влияют на зависимость спроса от цены и ценовые эластичности товаров (уровень дохода потребителей, наличие товаров-заменителей, воспринимаемая потребительская ценность).

Авторами предлагается модель, в которой для упрощения рассматриваются только два продукта: изучаемый продукт и базовый продукт (потребительская корзина). Удельная потребительская ценность изучаемого продукта и базового продукта задаются линейными функциями:

где — коэффициенты линейной зависимости.

Бюджетное ограничение записывается как

где — цена изучаемого продукта, зависящая от объёма , — фиксированная цена базового продукта, — доход домохозяйства.

Исходная система уравнений для максимизации суммарной потребительской ценности A при бюджетном ограничении R выглядит следующим образом:

Формула 3. Исходная система уравнений модели.

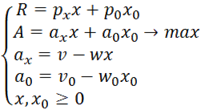
Здесь

R – доход домохозяйства. x₀ – количество потребительских корзин (обычно x₀ ≈ 1). При этом другое используемое название потребительской корзины в настоящей публикации – базовый продукт. p₀(x₀) – стоимость потребительской корзины (базового продукта). x – количество изучаемого продукта. p(x) – цена изучаемого продукта, которая является функцией от x. A – суммарная потребительская ценность. a – удельная потребительская ценность. v и w – коэффициенты линейной зависимости a от x. a₀ – удельная потребительская ценность базового продукта. v₀ и w₀ – коэффициенты линейной зависимости a₀ от x₀.

Подставим выражения для a₀ и a в функцию полезности A:

и упростим

Формула 4. Функция суммарной потребительской ценности

Теперь у нас есть функция суммарной потребительской ценности, которую мы можем максимизировать, но для этого нам нужно учитывать бюджетное ограничение. Чтобы решить задачу оптимизации, мы можем использовать метод Лагранжа, как и при выводе формулы Формула 1.

Решение исходной системы уравнений

Определим функцию Лагранжа:

Теперь найдем частные производные, приравняем их к нулю и составим из них систему из трёх уравнений.

Формула 5. Система уравнений, полученная методом Лагранжа, для оптимизации функции A(x₀,x)

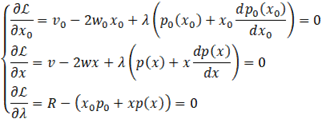
Прежде всего, решим дифференциальное уравнение, находящееся на второй позиции в системе уравнений формулы Формула 5, учтя, что при p=0, x=v/w (пояснения см. ниже). Получим следующее выражение для x:

Формула 6. Выражение для x.

Выразим таким же способом x₀ из первого уравнения формулы Формула 5.

Формула 7. Выражение для x₀.

Подстановкой получим λ:

Формула 8. Выражение для множителя Лагранжа.

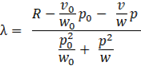
Теперь подставим λ из формулы Формула 8 в формулу Формула 6.

Формула 9. Искомая формула зависимости объёма покупок от цены изучаемого товара

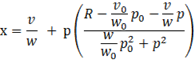
Критическое количество продукта (порог потребления)

Обратим теперь внимание на удельные потребительские ценности:

a = v – wx a₀ = v₀ – w₀x₀

Изобразим первое из этих уравнений на графике.

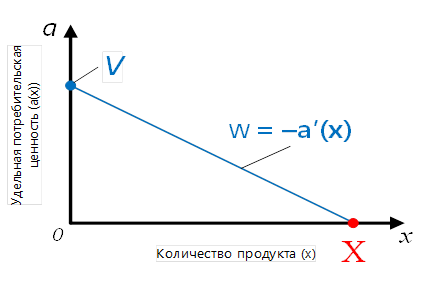
Рисунок 1. График зависимости a = v – wx

Как видим, первый бесконечно малый «кусочек» изучаемого продукта имеет потребительскую ценность a = v. Затем с ростом количества потребляемого продукта его ценность падает со скоростью , достигая при x = X (икс большое) нуля. При x > X количество потребляемого продукта становится избыточным, а его удельная потребительская ценность отрицательной. То есть X обозначает то количество изучаемого продукта, которое является критическим при потреблении, так что до этого значения потребительская ценность единицы продукта полезна, а после этого значения – вредна в виду его переизбытка в потреблении. При этом, как видно из графика, этот порог потребления изучаемого продукта равен:

Формула 10. Критическое количество изучаемого продукта.

По аналогии получаем также

Формула 11. Критическое количество базового продукта.

Отметим, что X₀ – это, по сути дела, базовый уровень потребления базового продукта, т.е. нормативная полная потребительская корзина, необходимая для здорового и комфортного проживания домохозяйства. Так же и X – это порог потребления изучаемого продукта.

В итоге, формула Формула 9 предстанет в виде:

Формула 12. Итоговая формула решения оптимизационной задачи в виде x=f(p)

Как видим, зависимость x от p оказалась квадратичной, как и в модели QUAIDS, что считается более точным способом отражения влияния нелинейных эффектов изменений цен и доходов потребителей на их спрос.

Формула Формула 12 состоит из двух частей:

· порога потребления X (критического количества), . Это количество продукта x, при котором его удельная потребительская ценность a становится равной нулю. . Эта часть не зависит от цены p.

· ценовой корректировки спроса . Эта часть зависит от цены p и определяет отклонение оптимального x от порогового уровня X.

Таким образом, общее потребление

Формула 13. Уравнение спроса.

Графический вид итоговой функции зависимости спроса от цены

Функция x=f(p), представленная формулой Формула 12 имеет колоколообразный графический вид, как это показано на рисунке Рисунок 2. При этом вид несколько меняется в зависимости от знака выражения в числителе формулы Формула 12. Обозначим это выражение как L (lever):

То есть

Формула 14. Формула для ценовой корректировки спроса.

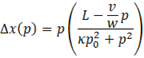
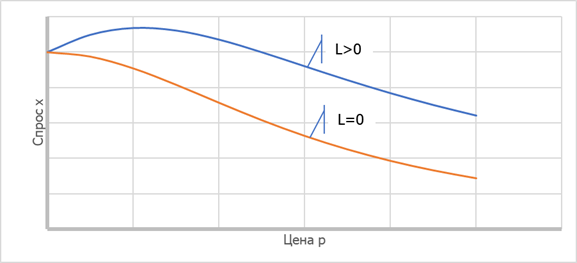
Рисунок 2. График зависимости спроса x от цены p в соответствии с формулой Формула 12

Кривая спроса в нашей модели при нулевой цене пересекает ось абсцисс в точке X, т.е. при нулевой цене оптимальным с точки зрения максимизации потребительской ценности будет потребление изучаемого продукта на уровне его критического количества X. Далее при росте цены спрос x либо некоторое время растёт (при L>0) либо сразу падает (при L=0) и далее при дальнейшем росте цены p стремится к нулю.

Феномен роста потребления исследуемого продукта при росте его цены

Обратим внимание на синюю линию графика на рисунке Рисунок 2. Такой вид кривой имеет место при L>0.

При малых ценах p, близких к 0, при L>0 числитель ценовой корректировки спроса , равен

Формула 15. Значение ценовой корректировки спроса при L > 0, p > 0 и

И поскольку все параметры в формуле Формула 15 предполагаются положительными, этот начальный наклон кривой спроса положителен.

После достижения определённого максимума, когда цена p становится достаточно большой, член в числителе начинает доминировать, делая числитель отрицательным. Это вызывает снижение x с ростом p, что соответствует классической теории.

Экономическая интерпретация феномена [10], [11]

Давайте разберёмся, что означает условие

Оно означает, что после покупки базового набора продуктов (потребительской корзины X₀) за цену p₀​ у домохозяйства остаётся неотрицательный остаток бюджета. Этот «избыточный» доход даёт ему финансовый «манёвр» на приобретение изучаемого продукта. Почему же приобретается именно изучаемый продукт x, причём даже выше его полезного количества X, а не базовый продукт x₀?

Дело в том, что по логике задачи ценность изучаемого продукта намного меньше ценности базового продукта, то есть всей потребительской корзины. Это верно также и для их удельных потребительских ценностей, а именно , поэтому при решении вопроса, куда потратить остаток средств: на превышение X₀ (базовый продукт) или на превышение X (изучаемый продукт), потребитель всегда будет выбирать в пользу изучаемого продукта, так как снижение потребительской ценности при избытке изучаемого продукта будет всегда меньше, чем при избытке базового.

Но это ещё не всё. Есть ещё две интересные экономические интерпретации.

Теневая цена денег

В классической микроэкономике при максимизации полезности и бюджетном ограничении частные производные полезности по количеству i-го товара дают выражение вида:

Здесь λ является предельной полезностью одного рубля расходов, вне зависимости от того, на какой товар он потрачен. Это и есть маржинальная (предельная) полезность денег.

Рассмотрим, какой вид зависимости получается в нашей модели для λ.

Перепишем уравнения формулы Формула 5 в таком виде:

Дифференцирование по x:

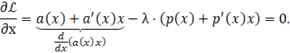
Или так:

Заметим, что . Поэтому

Формула 16

Дифференцирование по x₀​:

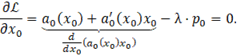
Или:

Заметим, что . Тогда

Формула 17

То есть выражения для теневой цены денег получаются такими же, как и в классической микроэкономике. Но в нашем случае всё-таки есть небольшая разность, диктуемая особенностью модели.

Далее через полный дифференциал получаем:

Формула 18. Полный дифференциал

Подставим в формулу Формула 18 значения дифференциалов из формул Формула 16 и Формула 17, получим и упростим

Таким образом,

Формула 19. Маржинальная полезность денег λ.

Как мы видим, множитель Лагранжа λ – это производная от оптимального значения целевой функции по бюджету R. Он показывает, насколько увеличится максимальная потребительская ценность при увеличении бюджета на одну единицу.

Выражая теневую цену денег λ через p, получим:

Формула 20.

Теперь подставим значение x из формулы Формула 12 выведем результирующее выражение для λ:

Формула 21. Теневая цена денег как функция от цены изучаемого продукта

График этой зависимости имеет вид:

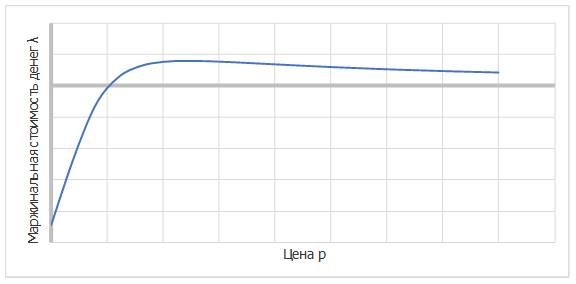
Рисунок 3. Вид зависимости маржинальной (теневой) стоимости денег от цены изучаемого продукта λ(p) при излишках семейного бюджета

В итоге, λ как теневая цена денег, показывающая, насколько изменится максимальная полезность при дополнительной единице бюджета ( ) при и оказывается меньше нуля. Свободный остаток бюджета делает эти «лишние» деньги менее ценными, а их предельную полезность отрицательной, так что потребитель может себе позволить приобретать изучаемый продукт сверх полезной нормы X, запасаясь им как бы впрок, пока продукт ещё более не подорожал.

Примечательна цена, при которой λ становится равной нулю, а потребитель снова готов приобретать только X изучаемого товара:

Формула 22. Цена возврата к классической зависимости спроса от цены.

Назовём её ценой возврата к классической зависимости спроса от цены. Она равна величине избыточного бюджета, делённой на норму потребления X.

Похожее явление, напоминаемое рассматриваемое, уже известно в экономике под названием эффект Гиффена.

Аналогия с эффектом Гиффена [12], [13]

Несмотря на то, что в классическом эффекте Гиффена рост цены на низкокачественный товар (например, картофель) приводит к увеличению его потребления из-за ограниченности дохода, а в данной модели аналогичный механизм возникает из-за нелинейной зависимости потребительской ценности от x и бюджетных ограничений, что создает зону, где x растет с ростом p, два этих явления имеют общие стороны. В нашей модели при избыточном бюджете (R−X₀p₀>0)>0 теневая цена денег λ оказывается отрицательной при малых p, что аналогично отрицательному доходному эффекту Гиффена: увеличение p чуть снижает реальный доход, но поскольку λ<0, потребитель «докупает» больше x до тех пор, пока λ не обнулится, то есть пока не исчерпается бюджет, и x вернётся к X.

В нашей модели при наличии избытка бюджета доходный эффект доминирует над субституционным, что обращает зависимость спроса от цены из обратно пропорциональной в прямую. Потребитель стремится «накупить» чуть больше изучаемого продукта, чтобы компенсировать утрату полезности денег.

Аномальный рост потребления в нашей модели при R−X₀p0>0 есть финансовый аналог классического эффекта Гиффена, где отрицательная теневая цена денег (λ<0) выполняет ту же роль, что отрицательный доходный эффект у инфериорного товара: в обоих случаях доходный эффект доминирует над субституционным, обращая знак dx/dp на некотором участке. В нашей модели роль отрицательного доходного эффекта для инфериорного товара выполняет отрицательная теневая цена денег

Результаты

Практическая верификация модели

Рассматриваемая оптимизационная модель с бюджетным ограничением позволяет составлять рейтинги продуктов, соотнося их потребительскую ценность с таковой же ценностью потребительской корзины на регулярной основе, опираясь на нормативы потребления и статистику цен и потребления.

Модель позволяет оценивать:

При этом p₀ и κ можно получить из данных рыночной статистики, X – из нормативов потребления, а X₀ принять за единицу (одна потребительская корзина).

Вывод регрессионного уравнения

Чтобы уйти от отрицательной теневой стоимости денег (λ<0), примем, что излишков семейного бюджета нет, и он равен потребительской корзине, то есть R–X₀p₀=0. Тогда наше выражение x=f(p) будет выглядеть так

Формула 23. Зависимость спроса от цены при положительной теневой стоимости денег

Если мы сможем получить из рыночной и федеральной статистики данные о парах , то, с помощью метода наименьших квадратов мы получим наши κ и X.

Чтобы обойти нелинейность по κ и X представим наше уравнение Формула 23 в следующем виде:

Обозначим

И получим искомое уравнение линейной регрессии:

Формула 24. Уравнение линейной регрессии для поиска κ и X.

Теперь собранные ряды из статистических данных за временные интервалы можно использовать для построение линейного графика M_t=f(Z_t) и определения искомых κ и X. При этом наши искомые параметры равны:

Статистика некоторых продуктовых групп

Для построения регрессионной модели были взяты ряды {(p_t,x_t)} на основе годовых отчётов Росстата [14] с линейной интерполяцией показателей. Данные приведены в реальных ценах 2024 года с устранением сезонности. Источником данных являются обследования бюджета домохозяйств, проводимых Росстатом, которые фиксируют потребление и расходы именно на уровне домохозяйства. Объёмы потребления (в кг или штуках) отражают суммарное потребление всех членов домохозяйства за месяц. В расчётах учитывался средний размер домохозяйства в России в размере 2,8 человека.

Данные интерполированы с шагом 6 месяцев для устранения сезонных колебаний. Цены скорректированы по формуле , где – месячная инфляция [15].

Цельное молоко

Таблица 1. Цены и объёмы потребления цельного молока домохозяйствами. Данные Росстата.

Месяц/Год	Цена (руб/кг)	Объём потребления, кг/мес
01.2020	57,8	22,5
07.2020	58,9	21,9
01.2021	61,6	20,9
07.2021	63,2	20,7
01.2022	70,8	19,5
07.2022	74,2	18,9
01.2023	78,1	18,8
07.2023	79,6	18,6
01.2024	81,9	18,6
07.2024	83,2	17,9

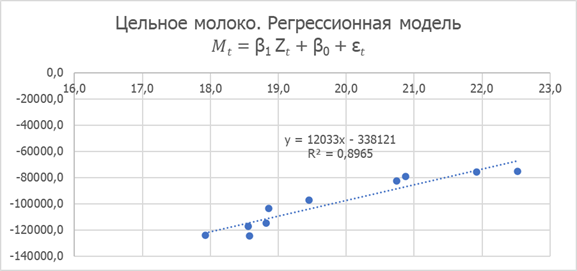
Рисунок 4. Цельное молоко. Регрессионная модель 𝑀_𝑡 = β₁ Z_𝑡 + β₀ + ε_𝑡

Параметры линейной регрессии:

β₁= 12033,2; β₀= -338120,9; κ= 4,5*10^-06; X= 28,1; r²=0,897

Говядина

Таблица 2. Цены и объёмы потребления мяса говядины домохозяйствами. Данные Росстата

Месяц/Год	Цена (руб/кг)	Объём потребления, кг/мес
01.2020	378	5,8
07.2020	387	5,7
01.2021	421	5,4
07.2021	434	5,5
01.2022	504	5,1
07.2022	532	4,9
01.2023	557	5,0
07.2023	567	5,0
01.2024	589	5,0
07.2024	605	4,8

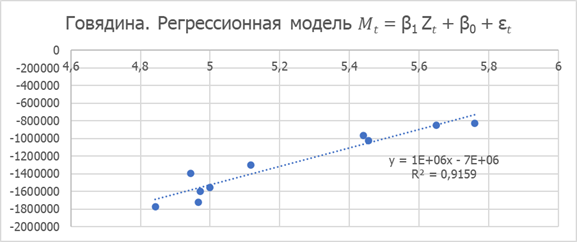
Рисунок 5. Потребление говяжьего мяса. Регрессионная модель 𝑀_𝑡 = β₁ Z_𝑡 + β₀ + ε_𝑡

Параметры линейной регрессии:

β₁= 1049425,16; β₀= -6772936,483; κ= 3,93*10^-04; X= 6,45; r²=0,916

Хлеб

Таблица 3. Цены и объёмы потребления хлеба домохозяйствами. Данные Росстата

Месяц/Год	Цена (руб/кг)	Объём потребления, кг/мес
01.2020	44,7	10,1
07.2020	45,8	9,9
01.2021	48,0	9,6
07.2021	49,4	9,5
01.2022	56,9	9,1
07.2022	59,4	8,8
01.2023	62,8	8,9
07.2023	63,5	8,6
01.2024	65,1	8,8
07.2024	66,7	8,3

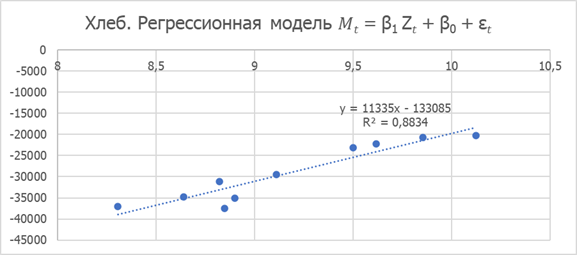
Рисунок 6. Хлеб. Регрессионная модель 𝑀_𝑡 = β₁ Z_𝑡 + β₀ + ε_𝑡

Параметры линейной регрессии:

β₁= 11334,77; β₀= -133085,38; κ= 4,24*10^-06; X= 11,74; r²=0,883

Обувь и повседневная одежда

Таблица 4. Цены и объёмы потребления обуви и повседневной одежды домохозяйствами. Данные Росстата

Месяц/Год	Цена (руб./ед.)	Объём потребления (ед./мес)
01.01.2020	1500	4,2
01.07.2020	1575	4
01.01.2021	1650	3,8
01.07.2021	1725	3,6
01.01.2022	1800	3,5
01.07.2022	1875	3,4
01.01.2023	1950	3,3
01.07.2023	2025	3,2
01.01.2024	2100	3,1
01.07.2024	2175	3

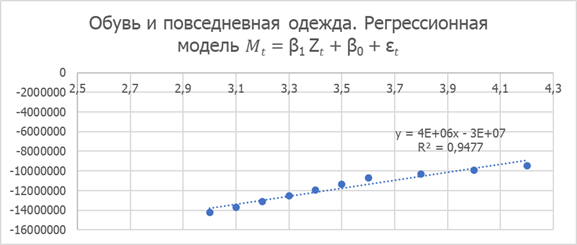
Рисунок 7. Обувь и повседневная одежда. Регрессионная модель 𝑀_𝑡 = β₁ Z_𝑡 + β₀ + ε_𝑡

Параметры линейной регрессии:

β₁= 4051361; β₀= -2,6*10^-07; κ= 0,001517; X= 6,4; r²=0,948

Бытовая химия и инвентарь, включая мелкие бытовые приборы

Таблица 5. Цены и объёмы потребления бытовой химии и инвентаря, включая мелкую бытовые приборы домохозяйствами. Данные Росстата

Месяц/Год	Цена (руб./ед.)	Объём потребления (ед./мес)
01.01.2020	450	6,5
01.07.2020	470	6,3
01.01.2021	490	6,1
01.07.2021	510	6
01.01.2022	530	5,9
01.07.2022	550	5,8
01.01.2023	570	5,7
01.07.2023	590	5,6
01.01.2024	610	5,5
01.07.2024	630	5,4

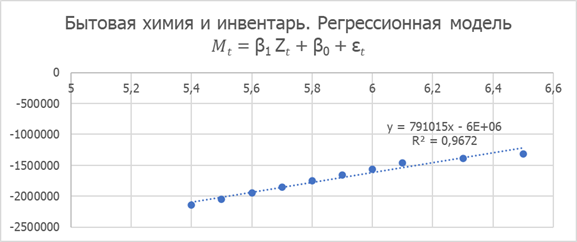
Рисунок 8. Бытовая химия и инвентарь. Регрессионная модель 𝑀_𝑡 = β₁ Z_𝑡 + β₀ + ε_𝑡

Параметры линейной регрессии:

β₁= 791015,4; β₀= -6364775; κ= 0,000296; X= 8,05; r²= 0,967

Мелкая мебель

Таблица 6. Цены и объёмы потребления мелкой мебели домохозяйствами. Данные Росстата

Месяц/Год	Цена (руб./ед.)	Объём потребления (ед./мес)
01.01.2020	8500	0,9
01.07.2020	8800	0,88
01.01.2021	9100	0,86
01.07.2021	9400	0,84
01.01.2022	9700	0,82
01.07.2022	10000	0,8
01.01.2023	10300	0,79
01.07.2023	10600	0,78
01.01.2024	10900	0,77
01.07.2024	11200	0,76

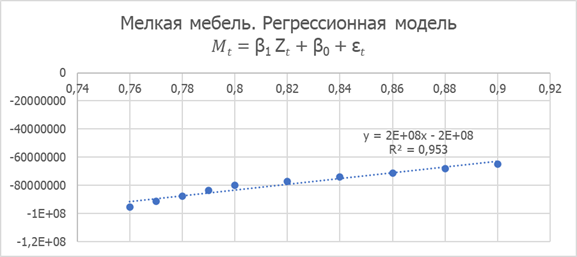
Рисунок 9. Мелкая мебель. Регрессионная модель 𝑀_𝑡 = β₁ Z_𝑡 + β₀ + ε_𝑡

Параметры линейной регрессии:

β₁= 2,04*10^-08; β₀= -2,47*10^-08; κ= 0,07651; X= 1,21; r²=0,953

Стоимость потребительской корзины

При расчётах параметров регрессионной модели (κ и X) были использованы данные о стоимости полной потребительской корзины Росстата [16, 17, 18, 19, 20], включающей:

· Все категории товаров и услуг (включая ЖКХ, транспорт, образование)

· Расходы на ребёнка (для домохозяйств с детьми)

· Нормы для активного социально-экономического потребления

Данные составлены по описи Росстата по фактическому потреблению домохозяйств. Корзина содержит 487 товаров и услуг. Данные являются средневзвешенными по ЦФО.

Таблица 7. Стоимость полной потребительской корзины для семьи из 2,8 человек (2 взрослых + 0,8 ребёнка).

Месяц/Год	Стоимость (руб./мес)	Источник данных
01.2020	34 726	Росстат, форма №1-ПК
07.2020	36 815 (+6.0%)	Индексы ИПЦ с коррекцией
01.2021	39 184 (+6.4%)	Отчёт Счётной палаты
07.2021	42 657 (+8.9%)	Данные РЭШ
01.2022	48 239 (+13.1%)	Аналитика ЦБ РФ
07.2022	53 874 (+11.7%)	Мониторинг Росстата
01.2023	58 912 (+9.3%)	Исследование ВШЭ
07.2023	62 345 (+5.8%)	Данные ФНС
01.2024	67 831 (+8.8%)	Прогноз Минэкономразвития
07.2024	72 156 (+6.4%)	Экспертная оценка

Итоговые рейтинги

Присвоим нашим параметрам понятные и осмысленные названия:

· κ – индекс эластичности потребительской ценности.

· X – порог потребления.

И внесём их в сводную таблицу.

Таблица 8. Индекс эластичности потребительской ценности, величина порога потребления и рекомендуемые нормы потребления для некоторых товарных категорий [21, 22, 23, 24, 25].

Товарная категория	Эластичность потребит. ценности	Порог потребления		Норма потребления, в год на д/хоз.
		в месяц	в год
Цельное молоко	4,5*10-06	28,1 кг	337,2кг	324,8 кг
Говядина	3,93*10-04	6,45 кг	77,4 кг	56 кг
Хлеб	4,24*10-06	11,74 кг	140,88 кг	179,2 кг
Обувь и повседневная одежда	0,001517	6,4 ед.	76,8 ед.	35 ед.
Бытовая химия и инвентарь, включая мелкие бытовые приборы	2,96*10-04	8,05 ед.	96,6 ед.	60,7 ед.
Мелкая мебель	0,07651	1,21 ед.	14,52 ед.	1,15 ед.

Как видим, по некоторым (в основном дешёвым продуктам) запросы населения (пороговая величина потребления) ниже рекомендуемых норм, а по другим продуктам (более дорогим) значительно выше.

Параметры, выведенные в нашей модели, позволяют сравнивать между собой потребительские ценности как отдельных товаров, так и товарных категорий, причём совершенно разных, сравнение которых эмпирически и в ходе социологических опросов дало бы неоднозначные результаты. Из диаграммы на рисунке Рисунок 10 видно, что индексы потребительской ценности хлеба и молока близки, хотя хлеб оценивается немного ниже молока. Индексы потребительской ценности мяса говядины и бытовой химии находится примерно на равном уровне. Индекс потребительской ценности мебели значительно опережает таковую других товарных категорий. Полученные параметры дают в руки специалистов сильный инструмент для рейтингования, сравнения и прогнозирования спроса, цен, воспринимаемой потребительской ценности – всего того, что необходимо для точного планирования предпринимательских и маркетинговых решений.

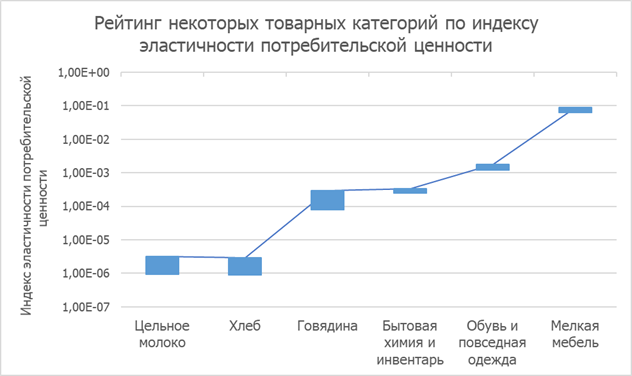
Рисунок 10. Рейтинг индексов эластичности потребительской ценности различных товарных категорий с учётом доверительных интервалов.

Обсуждение

Интерпретация ключевых параметров

· – порог потребления. Определяет потенциальную ёмкость рынка при нулевой цене. Для маркетолога это ориентир максимального объёма спроса, который можно достичь, например, при продвижении за счёт снижения цены продукта. А сравнение X с нормами потребления позволяет оценить степень удовлетворения потребностей.

· – индекс эластичности потребительской ценности. Это ключевой параметр модели, имеющий глубокий экономический смысл.

o Относительная скорость насыщения: κ показывает, насколько быстро убывает удельная ценность товара по сравнению с ценностью всей потребительской корзины . Низкое значение κ означает, что потребность насыщается медленно, и ценовые стимулы (скидки) будут долго эффективны. Высокое κ говорит о быстром пресыщении, при котором лучше делать упор на рекламу, отражающую ценность продукта, и дополнительные выгоды.

o Универсальная метрика относительной эластичности потребительской ценности: Параметр κ объединяет в себе как эластичность предельной полезности, так и субституционную эластичность потребления (dx/dx₀). Он показывает чувствительность потребительской ценности рубля, вложенного в товар, к изменению объёма потребления по сравнению с вложением в базовую корзину.

Обоснуем это, учтя, что κ является отношением скоростей убывания предельных полезностей (w и w₀) исследуемого и базового товара соответственно.

Тогда

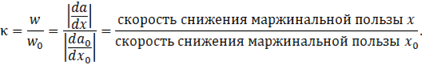
Но это ещё не всё. Ведь можно записать и так:

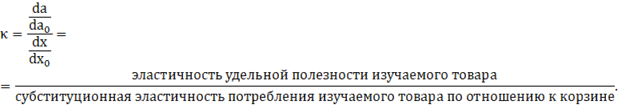
Что и требовалось доказать.

Практическое применение результатов моделирования

Результаты моделирования могут использоваться для:

· Оптимизации ценовых стратегий: Выбор между скидками (при низком κ) и акцентом на ценности (при высоком κ).

· Прогнозирования объёмов рынка: Использование X как верхней границы спроса.

· Сегментации продуктов: Кластеризация товаров по матрице (X,κ) для таргетинга.

· Государственного регулирования: Сравнение реального потребления (XX) с нормативами для выявления дефицита и разработки мер поддержки.

· Мониторинга кризисных явлений: Выявление аномалий спроса (эффект Гиффена) через анализ динамики λ(p).

· Вывода на рынок новых продуктов: Прогнозирование потенциала рынка на основе данных по схожим товарным категориям.

Возможные пути улучшения модели

1. Гетерогенность потребителей: Модель использует средние данные. Расчёт параметров для разных сегментов (по доходу, региону) позволил бы получить более точную картину.

2. Замещающие товары и сезонность: Модель не учитывает перекрёстную эластичность и сезонные колебания, которые могут влиять на X и κ.

3. Учёт эффекта Гиффена: Включение избыточного бюджета в регрессионную модель требует разработки «переключателя», который следовало бы добавить в модель с тем, чтобы он мог активировать этот эффект при определённых рыночных условиях.