Classification of scientific apparatus and decisions taken when comparing economic systems
Lapaev D.N.1
1 Нижегородский государственный технический университет им. Р.Е. Алексеева
Journal paper
Economic security (РИНЦ, ВАК)
опубликовать статью | оформить подписку
Volume 8, Number 5 (May 2025)
Abstract:
The problem of classifying a wide variety of tasks of comparative assessment of economic systems and optimization results has been repeatedly considered in specialized scientific works. Currently, due to the significant development of principles, approaches, methods and models of decision-making, accumulation of experience in studying applied optimization problems, there is an urgent need to expand the original classifications. The classification developed in the article focuses on the selection procedures and the specifics of the decisions formed in the context of multi-criteria, multi-projection and stakeholder choice. The classification combines nine bases: decision-making principles, scientific approaches, optimization methods, optimization models, decision-making rigidity, symmetry property, elimination of alternatives, and homogeneity of structure and comparability of decisions in dynamics. The article provides characteristic examples that reveal the classification. The author's classification will take an important place in the specialized theory and methodology and will be in demand in the study of a wide range of economic systems at various hierarchical levels for the study of urgent problems of assessing sustainability, security, innovation, efficiency, financial condition, etc.
Keywords: economic system, classification, comparative assessment, decision making, indicator, projection, stakeholder
JEL-classification: C38, C61, P51
Введение. Сравнительная оценка состояния систем как объектного [6] (Lapaev, 2016), так и проектного типов [14] (Lapaev, Potashnik, 2014) традиционно востребована экономической наукой и практикой [8, 9, 10] (Lapaev, Yurlov, 2008; Lapaev, 2006; Lapaev, Lapaeva, 2011). Такого рода анализ проводят различные стейкхолдеры [15, 21, 22] (Lapaev, Lapaeva, 2015; Lapaeva, 2017; Lapaeva, 2017), а сама оценка, как правило, осуществляется в многокритериальной или многопроекционной постановке [1, 2, 7] (Alenkova, Lapaeva, 2023; Lapaev, 2023; Lapaev, Lapaeva, 2014). Вопрос классифицирования широкого спектра задач сравнительной оценки состояния альтернатив многократно рассматривался [17, 18, 19] (Lapaeva, 2012; Lapaeva, 2014; Lapaeva, 2018) и дорабатывался [24] (Lapaeva, 2020) в профильных научных трудах. Сейчас в связи с существенным развитием принципов, подходов [23] (Lapaeva, 2017), методов [3, 4, 5] (Lapaev, 2024; Lapaev, 2024; Lapaev, 2024) и моделей многокритериального, многопроекционного и стейкхолдерского выбора, накоплением опыта решения прикладных оптимизационных задач [11, 12] (Lapaev, 2024; Lapaev, 2024) наблюдается явная потребность расширения исходных классификаций, чему и посвящена данная статья.
Взятая за основу наиболее подробная классификация [24] (Lapaeva, 2020), выполненная в логике проекционного подхода [23] (Lapaeva, 2017), охватывает 16 классификационных признаков: цель исследования, размер объекта, количество уровней анализа, уровень неопределенности, количество и состав проекций, количество и состав заинтересованных сторон, используемые методы проекционного выбора, фактор времени, используемые методы прогнозирования, используемые типы планирования, жесткость процедуры принятия решений, симметрия процедур сравнительной оценки, масштабность кластерообразования, задействование компьютерных технологий. Здесь в авторской классификации в рамках структурно-проекционного подхода сосредоточимся на процессах оптимизации и специфике генерируемых решений в контексте многокритериального, многопроекционного и стейкхолдерского выбора.
Описание классификации. Опираясь на актуальную теорию [3, 4, 5] (Lapaev, 2024; Lapaev, 2024; Lapaev, 2024) и практику сравнительной оценки состояния экономических систем [11, 12] (Lapaev, 2024; Lapaev, 2024), введем следующие основания и группы.
1. По принципам принятия решений. В многокритериальной постановке используют классический принцип Парето, а в многопроекционной постановке – профильные принципы многопроекционного выбора: принцип точечного, эффективного и квазиэффективного выбора.
2. По научным подходам. В многокритериальной постановке различают многокритериальный и структурно-критериальный подходы, в многопроекционной постановке – многопроекционный и структурно-проекционный подходы, в многосторонней – стейкхолдерский подход. Структурно-проекционный подход является основным, как обеспечивающий широкий охват различных аспектов и глубину исследования.
3. По методам оптимизации. В многокритериальной постановке задействуют метод ранжирования (основной) и метод главного показателя (дополнительный), в многопроекционной постановке – метод анализ-синтез и метод кластеризации (основные), метод исключения проекций и метод главной проекции (дополнительные), в многосторонней постановке – метод совмещения структур.
4. По оптимизационным моделям. В многокритериальной постановке оперируют многокритериальной модель, в многопроекционной постановке – многопроекционной моделью, в многосторонней – стейкхолдерской моделью, реализующими соответствующие методы оптимизации.
5. По жесткости принятия решений. Разграничивают жесткий (точечный), классический (эффективный) и мягкий (квазиэффективный) выбор при принятии решений одной или несколькими заинтересованными сторонами.
6. По свойству симметрии различают симметричный и асимметричный выбор. В многопроекционной постановке симметрией обладают решения, полученные на базе однородных (точечных, эффективных или квазиэффективных) решений проекций; задействование неоднородных множеств ведет к асимметричному выбору. В стейкхолдерском выборе симметрия трактуется как паритет решений соответствующих сторон, а диспаритет (ущемление позиций) приводит к асимметрии.
7. По выбытию альтернатив. В многокритериальной постановке реализуется как селективный, так и неселективный выбор. В многопроекционном и/или стейкхолдерском выборе возможна квазиселективность при выбытии экономических систем в одних проекциях и отсутствии отсева в других.
8. По однородности структуры. В многопроекционной постановке однородная кластерная структура состоит из одних кластеров или только из квазикластеров. Однородные взаимоприемлемые решения синтезируются на основе одноименных кластеров взаимодействующих сторон.
9. По сопоставимости решений в динамике. Важный аспект, поскольку научный аппарат многокритериального и особенно многопроекционного выбора достаточно широк и разнообразен, соответственно пути достижения цели разнятся. Сопоставимость имеет место, если применяемые на некотором временном интервале принципы, подходы, методы и модели принятия решений неизменны. В противном случае решения несопоставимы – сравнивать их некорректно.
Для пояснения сущности классификации приведем следующий пятипроекционный пример оценки состояния десяти систем S1–S10 (рис. 1-5). Требуется сформировать кластерную структуру на основании известных паретовских множеств проекций. Здесь и далее верхний индекс обозначает номер проекции, а нижний – номер показателя или альтернативы либо тип множества. Значению третьего показателя соответствует диаметр окружности. Предпочтительные направления изменения показателей обозначены стрелками.
Рассмотрим первую проекцию (рис. 1).
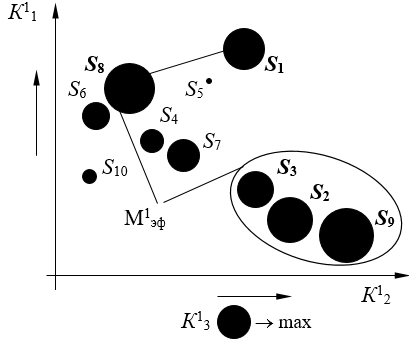
Рисунок 1. Эффективное решение в первой проекции, кластер 1
Источник: составлено автором.
Множество эффективных систем в первой проекции – М1эф = {S1, S2, S3, S8, S9} (выделено жирным шрифтом).
Обратимся ко второй проекции (рис. 2).
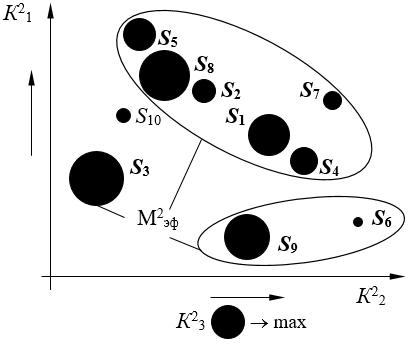
Рисунок 2. Эффективное решение во второй проекции, кластер 1
Источник: составлено автором.
Множество эффективных систем во второй проекции – М2эф = {S1, S2, S3, S4, S5, S6, S7, S8, S9}.
Перейдем к третьей проекции (рис. 3).
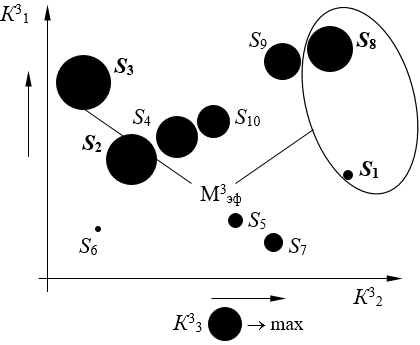
Рисунок 3. Эффективное решение в третьей проекции, кластер 1
Источник: составлено автором.
Множество эффективных систем в третьей проекции – М3эф = {S1, S2, S3, S8}.
Рассмотрим четвертую проекцию (рис. 4).
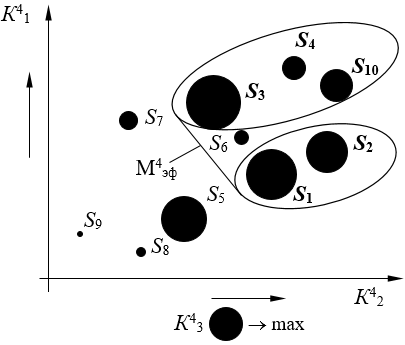
Рисунок 4. Эффективное решение в четвертой проекции, кластер 1
Источник: составлено автором.
Множество эффективных систем в четвертой проекции – М4эф = {S1, S2, S3, S4, S10}.
Обратимся к пятой проекции (рис. 5).
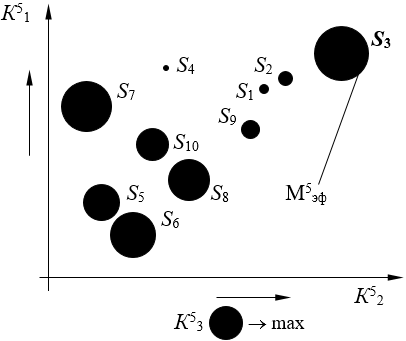
Рисунок 5. Эффективное решение в пятой проекции, кластер 1
Источник: составлено автором.
Множество эффективных систем в пятой проекции – М5эф = {S3}.
Синтезируем первый кластер (протоструктуру) М1КЛ = {S1, S2, S3, S8, S9}∩{S1, S2, S3, S4, S5, S6, S7, S8, S9}∩{S1, S2, S3, S8}∩{S1, S2, S3, S4, S10}∩{S3} = {S3}. Отметим, что максимально жесткий точечный выбор не даст результата. Так, М1т = {S9}, М5т = {S3} и решение отсутствует.
Далее аналогично находим второй М2КЛ = {S1, S2, S8, S9}∩{S1, S2, S4, S5, S6, S7, S8, S9}∩{S1, S2, S8}∩{S1, S2, S4, S10}∩{S2, S4, S6, S7, S8, S9, S10} = {S2} и третий М3КЛ = {S1, S8, S9}∩{S1, S4, S5, S6, S7, S8, S9}∩{S1, S8}∩{S1, S4, S10}∩{S1, S4, S6, S7, S8, S9, S10} = {S1} кластеры.
Квазиструктура в составе кластеров 1–3 однородна, поскольку получена посредством эффективного выбора по неизменному составу систем, проекций и показателей.
Выделим четвертый кластер из оставшихся систем S4–S10. Рассмотрим первую проекцию (рис. 6).
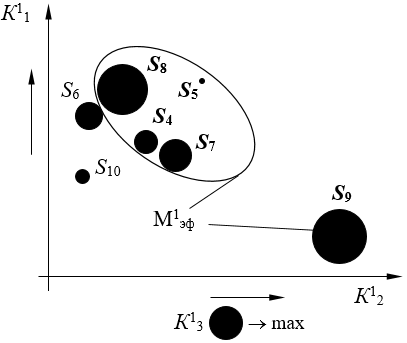
Рисунок 6. Эффективное решение в первой проекции, кластер 4
Источник: составлено автором.
Множество эффективных систем в первой проекции – М1эф = {S4, S5, S7, S8, S9}.
Перейдем ко второй проекции (рис. 7).
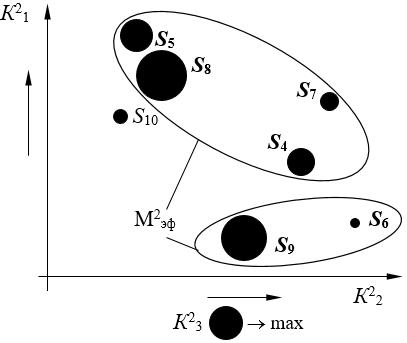
Рисунок 7. Эффективное решение во второй проекции, кластер 4
Источник: составлено автором.
Множество эффективных систем во второй проекции – М2эф = {S4, S5, S6, S7, S8, S9}.
Обратимся к третьей проекции (рис. 8).
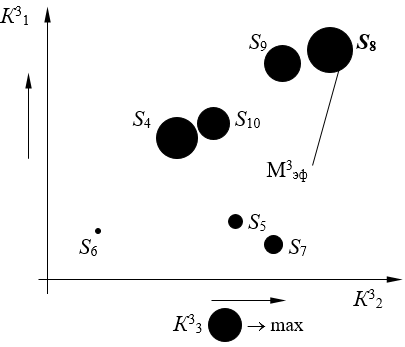
Рисунок 8. Эффективное решение в третьей проекции, кластер 4
Источник: составлено автором.
Множество эффективных систем в третьей проекции – М3эф = {S8}.
Рассмотрим четвертую проекцию (рис. 9).
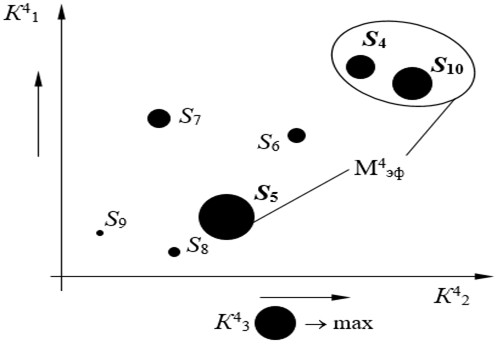
Рисунок 9. Эффективное решение в четвертой проекции, кластер 4
Источник: составлено автором.
Множество эффективных систем в четвертой проекции – М4эф = {S4, S5, S10}.
Перейдем к пятой проекции (рис. 10).
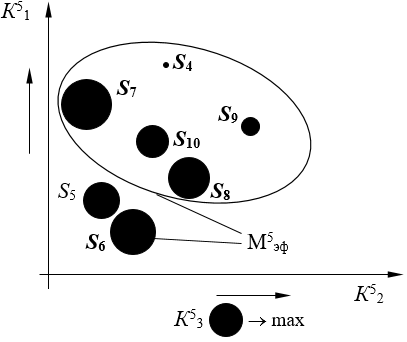
Рисунок 10. Эффективное решение в пятой проекции, кластер 4
Источник: составлено автором.
Множество эффективных систем в пятой проекции – М5эф = {S4, S6, S7, S8, S9, S10}. Четвертый кластер не сформирован: М4КЛ = {S4, S5, S7, S8, S9}∩{S4, S5, S6, S7, S8, S9}∩{S8}∩{S4, S5, S10}∩{S4, S6, S7, S8, S9, S10} = Ø. Задействуем вторые ранги и квазиэффективные множества.
В первой проекции подлежат рассмотрению альтернативы S6 и S10. Среди них доминирует вариант S6. Тогда множество квазиэффективных систем в первой проекции примет вид М1кэф = {S4, S5, S6, S7, S8, S9}.
Во второй проекции присутствует остаток в виде варианта S10, который финализирует множество квазиэффективных систем М2кэф = {S4, S5, S6, S7, S8, S9, S10}. В пятой проекции остаток содержит систему S5. Здесь М5кэф = {S4, S5, S6, S7, S8, S9, S10}. В проекциях 3 и 4 потребуются дополнительные расчеты.
Множество систем второго ранга в третьей проекции – М32р = {S4, S9}, а квазиэффективное множество – М3кэф = {S4, S8, S9}. Множество систем второго ранга в четвертой проекции – М42р = {S6, S7}, а квазиэффективное множество – М4кэф = {S4, S5, S6, S7, S10}.
Находим четвертый квазикластер М4КВ = {S4, S5, S6, S7, S8, S9}∩{S4, S5, S6, S7, S8, S9, S10}∩{S4, S8, S9}∩{S4, S5, S6, S7, S10}∩{S4, S5, S6, S7, S8, S9, S10} = {S4}. В силу отсутствия отсева экономических систем в проекциях 2 и 5 при построении четвертого квазикластера осуществлен симметричный, но квазиселективный выбор, достигнутый за счет проекций 1, 3 и 4.
Наряду с этим синтез возможен асимметричным селективным способом. В проекциях 2 и 5 ограничимся паретовскими множествами. Тогда М4КВ = {S4, S5, S6, S7, S8, S9}∩{S4, S5, S6, S7, S8, S9}∩{S4, S8, S9}∩{S4, S5, S6, S7, S10}∩{S4, S6, S7, S8, S9, S10} = {S4}. Отметим, что в данной схеме ни одна проекция не выбыла из оптимизационного процесса.
Квазиструктура в составе кластеров (квазикластеров) 1–4 неоднородна, ибо при синтезе четвертого кластера осуществлен более мягкий квазиэффективный выбор.
Обсудим аспект сопоставимости решений в динамике.
Продолжим наш пятипроекционный пример. Квазикластер М5КВ = {S5, S6, S7, S8, S9}∩{S5, S6, S7, S8, S9, S10}∩{S8, S9}∩{S5, S6, S7, S10}∩{S5, S6, S7, S8, S9, S10} = Ø не получен, и возможны различные направления раскрытия неопределенности. Например, исключение четвертой проекции. Тогда М5КЛ = {S5, S7, S8, S9}∩{S5, S6, S7, S8, S9}∩{S8}∩{S6, S7, S8, S9, S10} = {S8}. Четырехпроекционное решение имеется. Далее по аналогии можно найти нижестоящие кластеры по проекциям 1–3 и 5.
Если на другую дату удастся выделить сквозно кластерную структуру по всем пяти проекциям, то решения двух периодов будут несопоставимы ввиду отсутствия единства в используемых методах многопроекционной оптимизации.
Заключение
Разработанная классификация займет важное место в теории и методологии многокритериального, многопроекционного и стейкхолдерского выбора и будет востребована при исследовании широкого круга экономических систем на различных иерархических уровнях для решения актуальных задач оценки устойчивости [13] (Lapaev, Lapaeva, Potashnik, 2024), безопасности [1, 2] (Alenkova, Lapaeva, 2023; Lapaev, 2023), инновационности [16, 25] (Lapaev, Lapaeva, 2014; Morozova et al., 2010), эффективности [20, 28] (Lapaeva, 2015; Yurlov, Lapaev, Plekhanova, 2005), финансового состояния [26, 27] (Chernichenko et al., 2012; Chernichenko et al., 2013) и пр.
References:
Alenkova I.V., Lapaeva O.N. (2023). Security of the regions of the Central Federal District in the economic and innovative aspect. Razvitie i bezopasnost. (1(17)). 74-83. doi: 10.46960/2713-2633_2023_1_74.
Chernichenko A.N., Chernichenko L.L., Lapaev D.N., Shikhalieva D.S. (2012). Financial policy of the organization: theory and practice Mineralnye Vody: RGUPS.
Chernichenko A.N., Chernichenko L.L., Lapaev D.N., Shikhalieva D.S. (2013). Financial policy of the organization: theory and practice (textbook). International Journal of Experimental Education. (5). 132-133.
Lapaev D.N. (2006). Multi-criteria decision-making in economics Nizhny Novgorod: NGTU.
Lapaev D.N. (2016). Methodological approaches to the analysis and evaluation of economic security risks in social sphere. Naukovedenie. 8 (5(36)). 41.
Lapaev D.N. (2023). Security of the Volga federal district regions in the economic and innovation aspect. Economic security. 6 (1). 291-314. doi: 10.18334/ecsec.6.1.117300.
Lapaev D.N. (2024). A method for combining structures for stakeholder study of economic systems. Creative Economy. 18 (9). 2153-2174. doi: 10.18334/ce.18.9.121595.
Lapaev D.N. (2024). Method of multi-criteria ranking of economic systems. Economic security. 7 (8). 2085-2104. doi: 10.18334/ecsec.7.8.121607.
Lapaev D.N. (2024). Multi-projection assessment of security of regions of the central federal district in the economic and innovative aspect. Bulletin of the Nizhny Novgorod University. N.I. Lobachevsky. Series: Social Sciences. (3(75)). 28-35. doi: 10.52452/18115942_2024_3_28.
Lapaev D.N. (2024). Multi-projection assessment of the security of the regions of the Volga Federal District in the economic and innovative aspect. Economic security. 7 (2). 425-442. doi: 10.18334/ecsec.7.2.120476.
Lapaev D.N. (2024). Multi-projection clustering of economic systems. Journal of Economics, Entrepreneurship and Law. 14 (9). 4813-4826. doi: 10.18334/epp.14.9.121596.
Lapaev D.N., Lapaeva O.N. (2011). A multi-criteria comparison of alternatives in the economy Nizhny Novgorod: VGIPU.
Lapaev D.N., Lapaeva O.N. (2014). Making-up the methods of determination of preferable variants during the comparison of innovative activities of branches of industry by a combination of indices. Audit and financial analysis. (3). 373-375.
Lapaev D.N., Lapaeva O.N. (2014). Multi-criteria methods of the choice of preferable variants during the comparison of innovative activities of branches of industry. Audit and financial analysis. (5). 113-116.
Lapaev D.N., Lapaeva O.N. (2015). Principles of multi-projection decision making in economics. Audit and financial analysis. (4). 415-417.
Lapaev D.N., Lapaeva O.N., Potashnik Ya.S. (2024). Multi-projection assessment sustainability of the regions siberian federal district. Razvitie i bezopasnost. (2(22)). 90-99.
Lapaev D.N., Potashnik Ya.S. (2014). The valuation of capital of investment projects in industry. Audit and financial analysis. (5). 199-202.
Lapaev D.N., Yurlov F.F. (2008). Multi-criteria assessment of the economic condition of enterprises and industries, taking into account the interests of the parties Nizhny Novgorod: NGTU.
Lapaeva O.N. (2012). Classification of tasks for comparative evaluation of alternatives. Bulletin of Cherepovets State University. (1-2(37)). 45-48.
Lapaeva O.N. (2014). Classification of the problems of comparative assessment of alternatives in economics. Gumanizatsiya obrazovaniya. (5). 96-102.
Lapaeva O.N. (2015). Setting and analysis of the problems referred to multiple-view decision making in economics. Gumanizatsiya obrazovaniya. (3). 112-116.
Lapaeva O.N. (2017). Projective approach to comparative assessment of alternatives in economy. Modern science: current problems and ways to solve them. (1932)). 41-43.
Lapaeva O.N. (2017). The principle of a ranked choice of a mutually acceptable multi-projection predictive solution. Competitiveness in the global world: economy, science, technology. (1-1(26)). 105-108.
Lapaeva O.N. (2017). The principle of effective selection of a mutually acceptable multi-projection predictive solution. Competitiveness in the global world: economy, science, technology. (1-1926)). 102-104.
Lapaeva O.N. (2018). Classification of tasks of comparative evaluation of alternatives in the industrial economy Humanities and social sciences: problems and prospects. 12-15.
Lapaeva O.N. (2020). Development of classification of tasks for comparative assessment of the state of industrial economic systems Current issues of economics, management and innovation. 46-50.
Morozova G.A., Maltsev V.A., Maltsev K.V., Lapaev D.N. (2010). Innovative development of industrial complexes in the region Nizhny Novgorod: VVAGS.
Yurlov F.F., Lapaev D.N., Plekhanova A.F. (2005). Multi-criteria assessment and selection of effective solutions in the economy Nizhny Novgorod: NGTU.
Страница обновлена: 01.07.2025 в 17:28:10
