Динамические и стохастические задачи линейного программирования в логистике и управлении цепями поставок

Введение

Актуальность рассматриваемой проблемы заключается в том, что приложения методов математического программирования к логистике и управлению цепями поставок непрерывно расширяются. Представленный ниже обзор литературных источников, посвященных рассмотрению методов динамического и стохастического программирования применительно к логистической практике, показал, что, несмотря на широкий спектр проблем, которые охватывают методы динамического и стохастического программирования, новые практические задачи требуют совершенствования подходов к математической постановке задач и методам их решения.

Математическая постановка задач динамического и стохастического линейного программирования имеет немало общего. Во-первых, обе задачи являются многопериодными. Во-вторых, обе задачи требуют качественного и количественного описания исходных данных, но в динамической задаче качественное и количественное описание делается для каждого периода времени, а в стохастической задаче – для каждого их рассматриваемых сценариев. Существенным отличием данных задач является то, что в динамической задаче линейного программирования все исходные данные (такие как предложение, спрос, цены на ресурсы и прочие) являются постоянными в рамках рассматриваемого периода времени, поэтому динамическая задача является детерминированной, а в стохастической задаче некоторые исходные данные носят вероятностный характер, что требует рассмотрения нескольких сценариев в рамках рассматриваемого периода времени, реализация каждого из них имеет свою вероятность.

Так, детерминированная модель оптимизации может быть расширена и преобразована (модифицирована) в модель стохастического программирования, позволяющую одновременно проработать множество сценариев, а также учесть неопределенность и риски.

В данной работе рассматривается задача оптимизации отправок груженых контейнеров с «ММК-МЕТИЗ» (Открытое акционерное общество «Магнитогорский метизно-калибровочный завод») на контейнерный пункт железнодорожной товарной станции города Магнитогорска. Далее контейнерным поездом эти контейнерные грузы отправляются со станции к морским портам городов Новороссийска и Владивостока, и далее конечным потребителям за рубежом. Рассматриваемый нами участок цепи поставок ОАО «ММК-МЕТИЗ» представлен на рис. 1.

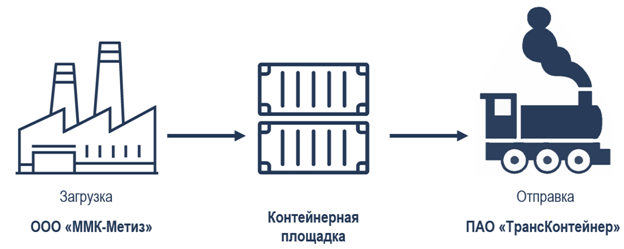
Рисунок 1 – Рассматриваемый участок цепи поставок ООО «ММК-МЕТИЗ» (составлено авторами)

В рассматриваемой цепи поставок ОАО «ММК-МЕТИЗ» при отправке контейнерных грузов с железнодорожной грузовой станции города Магнитогорска периодически происходят неполадки, некоторые из которых обусловлены сдвигами в порядке отправления составов ОАО «Трансконтейнер», а именно:

- приоритетом для ОАО «Трансконтейнер» могли стать другие товары, например предметы быта, в результате чего контейнеры с завода не могли попасть в ближайший состав;

- отсутствие фитинговых платформ, необходимых для отправки частных контейнеров морских линий, включая контейнеры ОАО «ММК-МЕТИЗ»;

- ОАО «Трансконтейнер» зачастую использует железнодорожные фитинговые платформы, прибывшие в адрес завода, для других нужд, в то время как загруженные контейнеры могут простаивать на станции в ожидании отправки.

Конечно, отказы происходят и по вине ОАО «ММК-МЕТИЗ» по следующим причинам:

- неритмичная реализация плана погрузки контейнеров на заводе;

- задержки в отправке контейнеров из-за отсутствия транспортных документов;

- простои контейнеров из-за ожидания дня отгрузки в соответствующее место назначения и по ряду других причин.

Научная гипотеза: в силу названных причин план погрузки и отправки контейнерных грузов ОАО «ММК-МЕТИЗ» на контейнерную площадку железнодорожной станции, выводимый в результате детерминированной постановки данной задачи, является нереалистичным. Нереалистичность детерминированной постановки задачи показана нами на примере численного решения задачи и анализа его результатов. Проблема связана с необходимостью в дополнительных ресурсах для бесперебойного процесса отправки контейнеров (погрузо-разгрузочных механизмах) и необходимость в дополнительных площадях для хранения груженых контейнеров.

Целью решаемой задачи является минимизация затраты на отправку контейнеров при возникновении сбоев в цепи поставок – задержек с отправкой контейнеров ОАО «ММК-МЕТИЗ» с железнодорожной товарной станции потребителям.

Логика решения рассматриваемой задачи стохастического программирования представлена на рис. 2. Здесь мы видим, что нас интересует определение оптимального количества загруженных x_j, складированных d_j и отправленных y_j контейнеров в течение первой и второй декады второго месяца при наличии задержек с их отправкой. При этом первая задержка в отправке контейнеров происходит в течение третьей декады первого месяца, а повторная задержка в течение первой декады второго месяца может не произойти (сценарий 1) или произойти (сценарий 2). Каждый из рассматриваемых сценариев реализуется с определенной вероятностью.

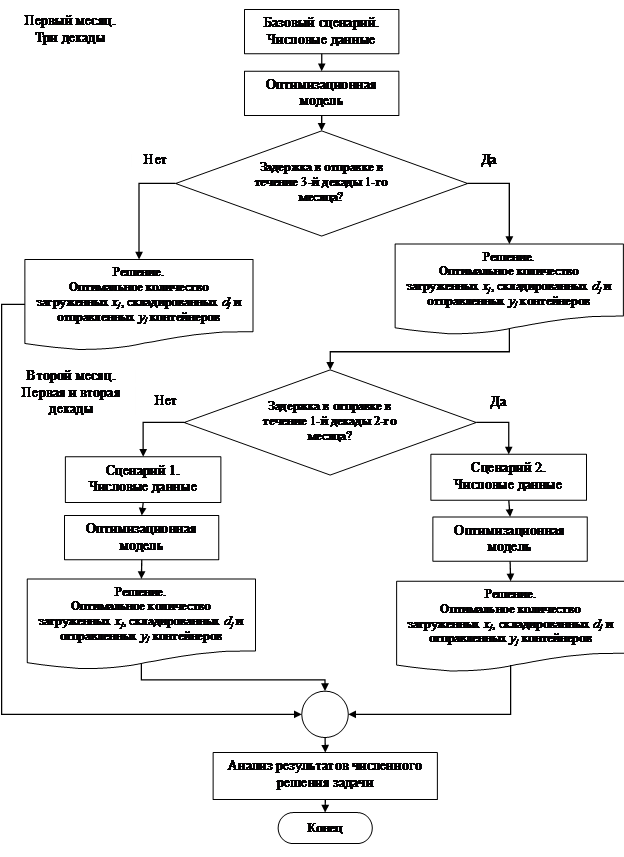
Рисунок 2 – Алгоритм решения поставленной задачи стохастического программирования (составлено авторами)

Научная новизна заключается в том, что авторами представлена индивидуальная математическая постановка стохастической задачи оптимизации отправок контейнерных грузов ОАО «ММК-МЕТИЗ» с железнодорожной товарной станции потребителям, разработан алгоритм ее численного решения и проведена апробация данного алгоритма на реальных данных.

Прежде чем мы начнем решать конкретную задачу, целесообразно изучить литературные источники по проблеме применения методов динамического и стохастического линейного программирования при решении логистических задач.

Обзор научной литературы по проблеме применения методов динамического и стохастического программирования в логистике

Динамические и стохастические модели линейного программирования успешно применяются в логистике для решения оптимизационных задач маршрутизации транспорта, производственного планирования, управления запасами и др. В данном контексте стохастическое программирование может применяться для моделирования вероятностных сценариев, что позволяет учесть случайный характер одного или нескольких параметров и принять решение на основе сравнения альтернатив.

К сожалению, российские авторы не уделили должного внимания проблеме использования методов динамического и стохастического программирования в логистике. Редким исключением из правила является монография Д.Б. Юдина и Е.Г. Гольштейна, в которой рассматриваются специальные задачи линейного программирования, среди которых задача о стратегии приобретения и продажи товаров в условиях изменяющегося спроса, представленная в виде модели динамического программирования [4, c. 159-164]. Теоретические основы динамического и стохастического программирования изложены в переведенной на русский язык монографии Дж. Шапиро [3, с. 449-463].

В рассмотренных нами научных работах зарубежных авторов представлены алгоритмы решения логистических задач, среди которых преимущественно встречается задача оптимизации складских и транспортных затрат при доставке товара Хсу П. и др. [12], Маджиони Ф. и др. [15], Карковс Е. и др. [8], Агазаде Д. и др. [5].

Помимо классических задач логистики, ряд литературных источников содержит решение оптимизационных задач в смежных с логистикой областях - экологии, энергопотреблении. Так, в работе [10] рассматривается стохастическая модель минимизации транспортных издержек наряду с минимизацией эмиссии парниковых газов. Алгоритмы решения задач минимизации энергопотребления, общей стоимости зарядки и затрат на оснащение парковок зарядными устройствами для электрических транспортных средств представлены в работах [13], [14] и [16].

Среди прочих областей решения подобных задач в изученной литературе можно выделить:

- производство - оптимизация времени производства и уровня качества деталей [19];

- энергетика - максимизация прибыли от эксплуатации гидроэнергетической системы [21]; минимизация затрат на выработку и потребление энергии [6], [22] и [23];

- гуманитарная сфера - оптимизация распределения гуманитарной помощи [18]; минимизация затрат на принятие решения при стихийных бедствиях [24];

- лесозаготовительная промышленность - максимизация заготовляемого объема дров [11];

- банковское дело - минимизация процентного риска [7].

Как видно из представленного множества моделей, в большинстве научных работ в качестве критерия оптимизации используется минимизация затрат - она составляет 65% всех критериев. Наряду с этим в нескольких источниках критерием решения задачи выступает максимизация прибыли ( [9]; [21]) и чистых дисконтированных доходов ( [20]).

В подавляющем большинстве задач рассмотрены однопродуктовые модели, многопродуктовые же – только в 10% случаев. Что касается однопериодных моделей, они встречаются в 65% случаев.

Табл. 1 содержит обобщенные выводы из проведенного анализа научной литературы по вопросам применения методов динамического и стохастического линейного программирования в логистике. Информация о всех рассмотренных моделях систематизирована по следующим критериям: 1) число видов продукции, рассматриваемых в модели; 2) является модель однопериодной или многопериодной; 3) учитываемые в модели ограничения; 4) критерий (критерии) оптимизации; 5) метод решения задачи; 6) какие исходные данные носят вероятностный характер, т.е. какие неопределённости рассматриваются в задаче.

Таблица 1 – Резюме обзора литературного обзора по вопросам применения методов динамического и стохастического линейного программирования в логистике (составлено авторами)

Анализ, представленных в табл. 1 работ, показал, что методы динамического и стохастического программирования непрерывно развиваются, в частности, достаточно часто используются методы многоступенчатого стохастического программирования, двухэтапного стохастического программирования и эвристические алгоритмы.

Содержательная постановка задачи

Содержательная постановка рассматриваемой задачи подробно была рассмотрена в работах [1] и [2], поэтому в данной статье опишем ее кратко.

Грузы своим потребителям ОАО «ММК-МЕТИЗ» может отправлять как 20-футовыми, так и 40-футовыми контейнерами. Доставка контейнеров с завода на железнодорожную товарную станцию города Магнитогорска может быть осуществлена как собственным, так и наемным автотранспортом. Существуют три способа загрузки контейнеров: 1) загрузка на полу и погрузка на полуприцеп с использованием крана; 2) загрузка на полу и погрузка на полуприцеп с использованием домкратов; 3) загрузка контейнера без снятия его с полуприцепа (загрузка в автомобиль). Таким образом, имеется два типа контейнеров, два типа автотранспорта и три способа погрузки контейнеров, что приводит к 12 вариантам отправки груженых контейнеров, отличающихся затратами.

Альтернативные варианты отправки груженых контейнеров представлены на рис. 3. Задача заключается в определении оптимального количества загруженных x_j, складированных d_j и отправленных y_j контейнеров j-го типа, при которых затраты являются минимальными.

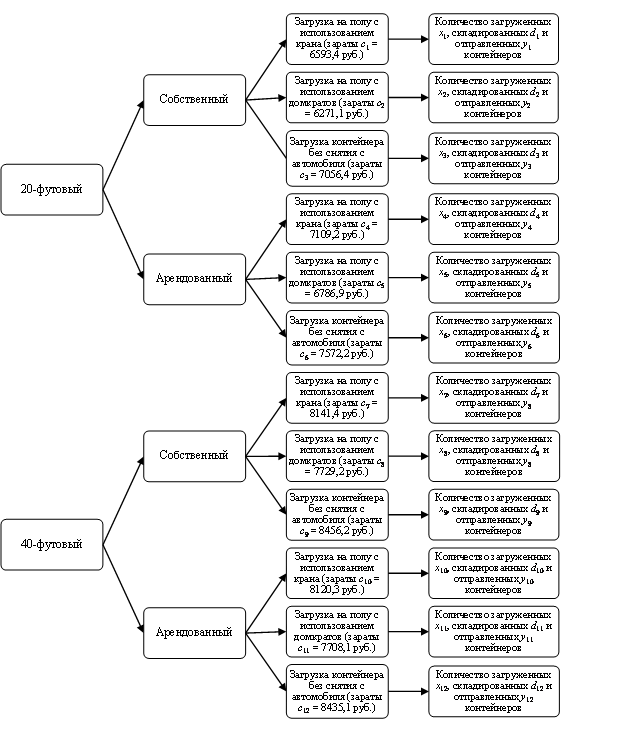
Рисунок 3 – Альтернативные варианты отправки груженых контейнеров

(составлено авторами)

Существенным обстоятельством является то, что в рассматриваемой задаче имеется ряд ограничений, которые необходимо учитывать при ее решении:

1) ограничения на количество контейнеров, которые загружаются на полу и, соответственно, должны быть погружены на автотранспорт с использованием крана или домкратов;

2) ограничения на количество грузов, которые должны быть отправлены 20- и 40-футовыми контейнерами;

3) ограничения на вместимость заводского склада для хранения груженых контейнеров;

4) ограничения, учитывающие неравномерность производства продукции на ОАО «ММК-МЕТИЗ» и соответственно неравномерность загрузки контейнеров.

Кроме того, необходимо учитывать возможные задержки с отправкой контейнеров с железнодорожной товарной станции города Магнитогорска потребителям.

Опишем подробнее предлагаемую модификацию имеющейся проблемы. Задача рассматривает смежных три периода (декады), в течение которых возможны задержки с отправкой контейнеров:

- третья декада первого месяца (в этот период происходит первый сбой);

- первая декада второго месяца (в этот период возможен повторный сбой (задержка с отправкой контейнеров) с определенной вероятностью);

- вторая декада второго месяца (предполагаем, что в этот период сбоя не будет).

Таким образом, в рассматриваемой задаче возможны три сценария.

Базовый сценарий: отсутствие сбоя (задержки с отправкой контейнеров). Следует отметить, что в этом случае задача не является стохастической. Базовый сценарий необходим, чтобы оценить увеличение затрат в случае возникновения сбоев с отправкой контейнеров.

Сценарий 1. Сбой происходит только на третьей декаде первого месяца, сбоя в течение первой и второй декады второго месяца нет; сценарий 1 реализуется с вероятностью p₁ = 0,7;

Сценарий 2. Происходят подряд два сбоя, первый сбой происходит в течение третьей декады первого месяца, второй – в течение первой декады второго месяца; сценарий 2 реализуется с вероятностью p₂ = 0,3.

Суть задачи заключается в рассмотрении двух сценариев одновременно, т.е. задержки при отправке контейнеров, которая происходит только в третьей декаде первого месяца, при отсутствии задержки в течение второго месяца (с вероятностью p₁ = 0,7) и повторной задержки при отправке контейнеров в течение первой декады второго месяца (с вероятностью p₂ = 0,3).

В результате решения задачи мы должны полить ответы на следующие вопросы.

1. Имеет ли эта задача решение без ослабления ограничений по площади хранения контейнеров и по способам их загрузки?

2. Если задача не имеет решения без ослабления ограничений, то какие конкретно ограничения должны быть ослаблены?

3. Насколько возрастут затраты при реализации сценариев с задержкой отправки контейнеров по сравнению с базовым сценарием?

В целом, решение этой задачи должно ответить на вопрос о том, какими дополнительными ресурсами должен обладать грузоотправитель – ОАО «ММК-МЕТИЗ» – для того, чтобы обеспечить отправку в течение месяца всего объема произведенной продукции в случае возникновения задержек с отправкой контейнеров.

Математическая постановка задачи

Опишем математическую постановку стохастической задачи оптимизации отправок контейнерных грузов.

Предлагается использовать такие обозначения:

– индексы, обозначающие типы контейнеров;

– индексы для обозначения способов отправки контейнеров;

– индексы для идентификации периода планирования, где – третья декада первого месяца, – первая декада второго месяца, – вторая декада второго месяца;

– количество контейнеров i-го типа, которые были загружены j-м способом в определённый период t;

– предельное число контейнеров i-го типа, которое возможно загрузить j-м способом, в период t;

– число контейнеров i-го типа, которые были загружены j-м способом и отправлены на железнодорожную станцию, в период t;

– число складированных контейнеров i-го типа, которые были загружены j-м способом, в начале периода t;

– число складированных контейнеров i-го типа, которые были загружены j-м способом, в конце периода t;

– издержки на отправку 1 контейнера типа i, который был загружен способом j, в период t;

– сбор за предъявление раньше требуемого срока контейнера i-го типа, загруженного j-м способом, в период t;

– масса [брутто] загруженной продукции в контейнер i-го типа;

– масса продукции, отправленной в контейнерах i-го типа, в период t;

– масса продукции, которая должна быть загружена в контейнеры в период t;

– масса продукции, которая может быть отправлена в период t (ограничение по отправке);

– общий объём отгруженной за месяц продукции.

Общая целевая функция рассматриваемой стохастической задачи L выглядит следующим образом (1):

(1)

где – затраты на отправку контейнеров в течение третьей декады прошлого месяца (базовый сценарий с задержкой в отправке контейнеров); и – затраты на отправку контейнеров в течение первых двух декад текущего месяца в соответствие со сценариями 1 и 2; и – коэффициенты, которые представляют собой соответственно вероятности реализации сценария 1 и 2.

Таким образом, для каждого k-го сценария необходимо найти значения переменных и , минимизирующих значения целевой функция (2):

. (2)

при ограничениях, которые для сценария 1 имеет вид (3) – (11):

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

В рассматриваемой задаче ищутся в задаче значения и на интервале , т.е. для первой и второй декады второго месяца.

Формулой (3) выражаются ограничения по вместимости склада. В левой части данного ограничения рассчитывается количество контейнеров на заводском складе, которое равно числу складированных контейнеров в начале данного периода плюс количество загруженных контейнеров минус количество отправленных контейнеров . Формула (4) уравнивает количество загруженных и отправленных различными способами контейнеров. Формулой (5) выражено ограничение по числу контейнеров i-го типа для загрузки j-м способом за время t. Формула (6) представляет ограничение на количество контейнерных грузов, требующих загрузки в период t. Ограничение по числу контейнерных грузов, которые могут быть отправлены в период времени t, выражается формулой (7). Формулой (8) представлено ограничение на количество грузов, отправленных в контейнерах i-го типа. Ограничение, выражаемое формулой (9), обеспечивает сбалансирование числа загруженных и отправленных контейнеров в течение всего периода планирования.

При решении данной задачи необходимо также учесть ограничения на неотрицательность , и (10) и целочисленность переменных и (11).

Для сценария 2, в котором моделируется возможный сбой, ограничения несколько видоизменяются (12) – (21):

(12)

(13)

(14)

; (15)

(16)

(17)

(18)

(19)

(20)

(21)

Таким образом, в сценарии 2 также ищутся в задаче значения и , но для периода , т.е. только за вторую декаду второго месяца, так как значения для первой декады второго месяца являются постоянными величинами, а значения принимаются равными 0, поскольку моделируется задержка в отправке контейнеров. Смысл других ограничений в системе (12) – (21) полностью соответствует смыслу рассмотренных выше ограничений (3) – (11).

Надо заметить, что ограничения по площади хранения контейнеров в конце концов были ослаблены в задаче, т.к. без их ослабления задача не имеет решения. Логично предположить, что компания ОАО «ММК-МЕТИЗ» найдет на территории завода площадь для хранения дополнительных (неотправленных в срок) груженых контейнеров, либо заплатит своему контрагенту – компании ОАО «ТрансКонтейнер» – сбор за преждевременное предъявление грузов.

Пример численного решения задачи и анализ результатов

Численное решение стохастической задачи оптимизации отправок контейнерных грузов было получено в Excel с помощью надстройки «Поиск решения». Описание табличная модель данной задачи, которое является довольно громоздким, в данной статье не представлено, но фрагменты внешнего вида рабочего листа Excel с исходными данными задачи и результатами решения задачи для первой декады базового сценария представлены в табл. 2. Аналогично формируется табличная модель для численного решения задачи в соответствии с первым и вторым сценарием.

Таблица 2 – Исходные данные и результаты численного решения задачи – подмодель для первой декады базового сценария (составлено авторами)

Таблица 3 – Анализ найденных решений по всем сценариям (составлено авторами)

Продолжение табл. 3

Анализ решения, представленного в табл. 3, показывает:

1. Общее количество отправленных контейнеров при решении стохастической задачи увеличивается с 64 до 69 ед., т.к. возможности для их оптимальной загрузки сокращаются (меньшее количество периодов планирования, необходимо отправлять контейнеры, не отправленные в прошлом месяце).

2. По сравнению с базовым сценарием более чем втрое (с 3 до 10 ед.) увеличивается количество 40 футовых контейнеров, затаренных на полу и погруженных с помощью крана, но с 12 до 9 ед. сокращается количество 20 футовых контейнеров с тем же способом погрузки.

3. По сравнению с базовым сценарием увеличивается количество как 20 футовых контейнеров, так и 40 футовых контейнеров затаренных на полу и погруженных с помощью домкратов с 5 до 6 ед. и с 8 до 13 ед. соответственно.

4. По сравнению с базовым сценарием с 22 до 14 ед. сокращается количество 20 футовых контейнеров, но с 14 до 17 ед. увеличивается количество 40 футовых контейнеров с затаркой в автомобиль.

5. По сравнению с базовым вариантом значительно на 10 единиц (с 39 до 29 ед.) сокращается количество отправленных 20 футовых контейнеров, но в то же время на 15 единиц (с 25 до 40 ед.) увеличивается количество отправленных 40 футовых контейнеров.

6. Очевидно, что общие затраты при наличии сбоя (задержки) в отправке контейнеров, составляющие 486,7 тыс. руб., выше, чем в базовом сценарии (при отсутствии сбоя) – 458,4 тыс. руб. Главная причина увеличения затрат на 6,18% при наличии сбоев – необходимость использования большего количества контейнеров.

Следует отметить, что данная задача содержит лимитирующие ограничения двух видов. Во-первых, ограничения по способам загрузки – не более 5 контейнеров должно быть загружено с помощью крана и не более 5 контейнеров должно быть загружено с помощью домкратов в течение каждого из периодов. Во-вторых, ограничение по вместимости склада – это ограничение на максимальное количество груженых 20 футовых и 40 футовых контейнеров, которые могут храниться на территории завода. Ограничение по вместимости склада является довольно жестким, и рассматриваемая задача не имеет решения без ослабления данного ограничения. В Сценарии 2 это ограничение ослаблено в большей степени (), чем в Сценарии 1 ().

Таким образом, численный пример решения этой задачи показал, что в случае возможных сбоев, т.е. задержек с отправкой контейнеров с железнодорожной товарной станции, компании ОАО «ММК-МЕТИЗ» необходимо иметь дополнительные контейнеры и дополнительные складские площади для хранения загруженных контейнеров. В то же время, погрузо-разгрузочного оборудования вполне достаточно как при плановом графике отгрузок, так и при внеплановых отгрузках при наличии сбоев в отправке контейнеров.

Заключение

Предложенная авторами модель стохастической задачи оптимизации отправок контейнерных грузов позволит компании оценивать свои риски и затраты при отправке контейнеров, учитывать неопределённости и вероятности наступления событий. Это важно в условиях реальной жизни, в условиях, максимально приближенных к практике, что дополнительно подчёркивает полезность и важность модели. Модель доработана, в ней учитываются повторные сбои в отправке контейнеров, учитываются не отправленные с прошлого месяца контейнеры, исследуются повторные задержки в отправке контейнеров, принимается во внимание вероятность повторного сбоя отправки.

Кроме того, предложенная модель даёт как детальное решение (чётко известно, какие способы погрузки и какие типы контейнеров нужно использовать), так и более общую картину – например, увеличение совокупных затрат, необходимость в дополнительных ресурсах для бесперебойного процесса отправки контейнеров (необходимость в дополнительных площадях для хранения груженых контейнеров). Стохастическая природа рассматриваемой задачи позволяет адаптировать её под разные сферы, к примеру, если у какой-либо компании есть похожий процесс в цепи поставок, но вероятность сбоя – иная, простым изменением параметров можно адаптировать предложенную модель под собственные запросы.